目录
[示例 1](#示例 1)
3)补充一个困扰我比较久的问题(虽然是个小问题):补充一个困扰我比较久的问题(虽然是个小问题):)
[图的存储里为什么用vector g[N]而不是vector g???](#图的存储里为什么用vector g[N]而不是vector g???)
[示例 1](#示例 1)
注:本文所有题目均来自蓝桥杯官网公开真题,仅做算法学习,代码皆由本人做出来并附上解析!
一,Floyd算法
1)简介及代码
先普及一下:
啥是单源最短路?啥是全源最短路?
1.单源最短路(SSSP):指定一个固定的"起点节点",计算该起点到图中所有其他节点的最短路长度及路径本身
2.全源最短路(APSP):计算图中每一对节点(u,v)之间的最短路径
1.Floyd:适合稠密图(点少,边多)
Floyd算法是一种求解"多源最短路"问题的算法,在Floyd算法中,图一般用领接矩阵来存储(n<=500),边权可正可负(但不允许负环),负环的定义:负环是指图中存在一个环(从某个顶点出发,经过若干条边后能回到该顶点),且构成这个环的所有边的权重之和为负数。若出现负环,则会一直绕圈,直至无穷小。
利用动态规划思想,逐步求解出任意两点之间的最短距离,我们需要准备的东西很少,只要一个d数组:int d[N][N][N],初始为正无穷。
d[k][i][j]表示路径(除去起点和终点)中编号最大的点编号<=k的情况下,点i到点j的最短距离,
但是实际上k这一维度是可以优化掉的,所以直接用int d[i][j];表示考虑到当前情况下,点i到点j的最短距离
简单概述:如果从 A 到 B 经过中间点 C 比直接走更近,那就更新 A 到 B 的距离。
具体来说,它的思路很像我们平时找路:
先记下所有点之间的直接距离(比如 A 到 B 直接走要 10 分钟),然后尝试用第一个点当 "中转站",看看有没有更短的路(比如 A-->X-->B 只要 8 分钟,就把 A 到 B 的距离改成 8)
再换第二个点当中转站,继续检查所有路线是否能更短。
把每个点都当一次中转站后,最后得到的就是所有点之间的最短距离。
这个算法的好处是简单直接,不管图里的边是正数还是负数(只要没有绕一圈反而距离变短的 "负环"),都能算出结果。缺点是效率不算太高,适合处理点比较少的图(比如几百个点)。
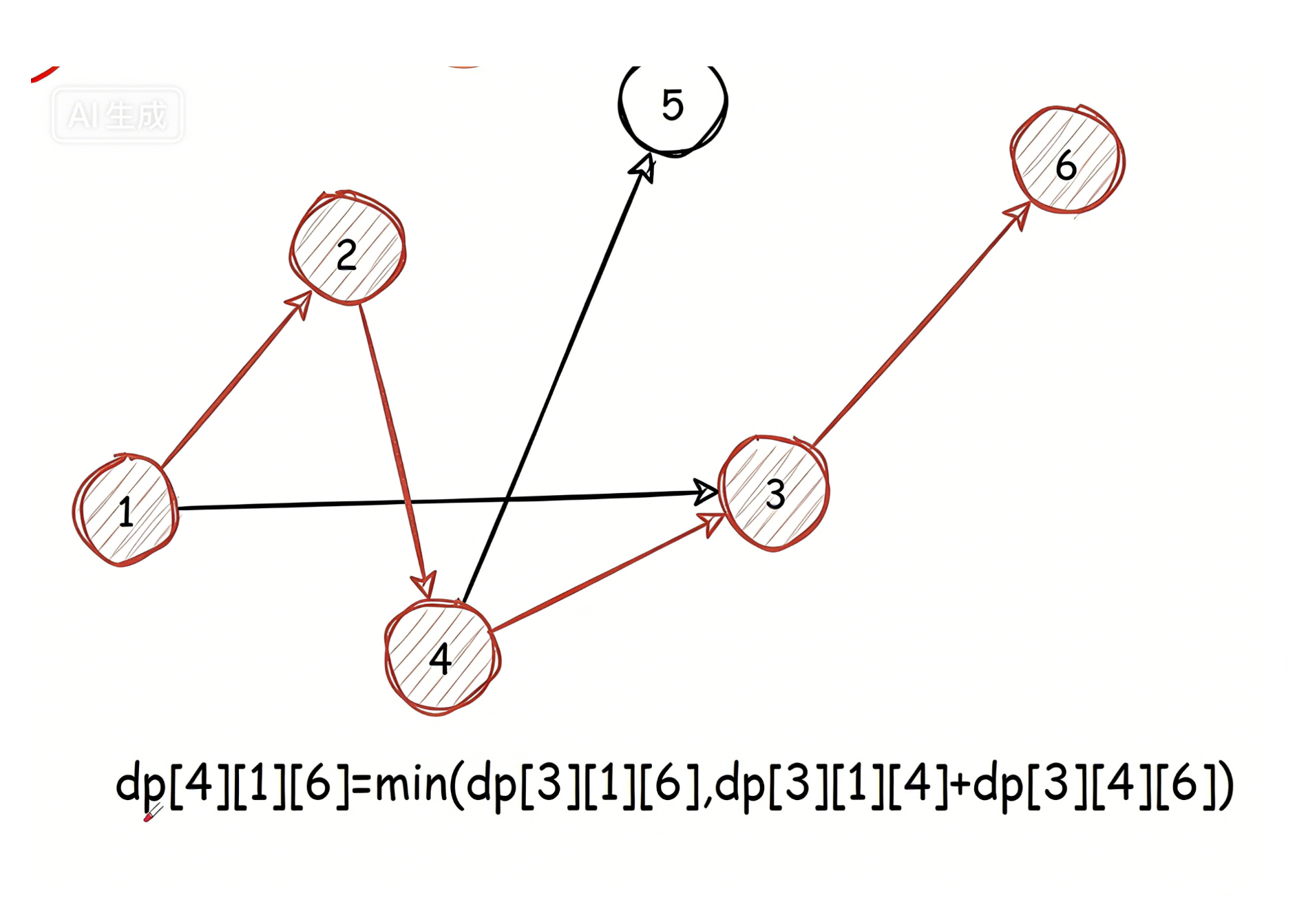
在这张图中,就表示中转编号不超过4的1-->6最短路径(可以是1->2->4->6,也可以是1->3->6)
就相当于中转编号不超过3的1-->3-->6最短路径和中转编号不超过4的1-->2-->4-->最短路径取最小的。
代码非常简单:
cpp
for (int k = 1; k <= n; k++)//枚举中转点
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; i <= n; j++)
{
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}在 Floyd 算法中,k(中转点)必须放在外层循环,核心原因是由算法的动态规划逻辑决定的
------ 它要保证:当用k作为中转点时,所有 "经过前k-1个点" 的最短路径已经计算完成。对于每一个中转站k点,都要遍历所有的i,j起始点。
通过这段代码我们不难看出,Floyd 算法的时间复杂度为 O (n^3),是比较高的,所以一般只能处理 n <= 500 的问题。这也是一个提示,当遇到 n<=500 的图论问题时,可以考虑使用 Floyd 算法。
2)例题
蓝桥杯官网------蓝桥公园
题目描述
小明喜欢观景,于是今天他来到了蓝桥公园。已知公园有 N 个景点,景点和景点之间一共有 M 条道路。小明有 Q 个观景计划,每个计划包含一个起点 st 和一个终点 ed,表示他想从 st 去到 ed。但是小明的体力有限,对于每个计划他想走最少的路完成,你可以帮帮他吗?
输入描述
输入第一行包含三个正整数 N,M,Q第 2 到 M+1 行每行包含三个正整数 u,v,w,表示 u↔v 之间存在一条距离为 w 的路。第 M+2 到 M+Q−1 行每行包含两个正整数 st,ed,其含义如题所述。
1≤N≤400,1≤M≤N×(N−1)/2,Q≤10^3,1≤u,v,st,ed≤n,1≤w≤10^9
输出描述
输出共 Q 行,对应输入数据中的查询。若无法从 st 到达 ed 则输出 −1。
输入输出样例
示例 1
输入:
3 3 3
1 2 1
1 3 5
2 3 2
1 2
1 3
2 3输出:
1
3
2代码详解:
cpp
#include <iostream>
using namespace std;
using ll=long long;
const ll N=409;
const ll inf=2e18;
ll dp[N][N];
int main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
int n,m,q;cin>>n>>m>>q;
//初始化距离为无穷大
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
dp[i][j]=inf;
}
}
//自己到自己的距离是0
for(int i=1;i<=n;i++) dp[i][i]=0;
//更新单边距离
for(int i=1;i<=m;i++)
{
//int u,v,w;cin>>u>>v>>w;数据类型要设置为相同的ll!!!
ll u,v,w;cin>>u>>v>>w;
dp[u][v]=min(dp[u][v],w);
dp[v][u]=min(dp[v][u],w);
}
//更新所有点的距离:
for(int k=1;k<=n;k++)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
}
}
}
while(q--)
{
int x,y;cin>>x>>y;
cout<<(dp[x][y]==inf?-1:dp[x][y])<<endl;//注意题目要求!
}
return 0;
}二,Dijkstra算法
1)简介
2,Dijkstra:用于稀疏图(点多,边少)
Dijkstra,迪杰斯特拉,又译做迪杰斯彻,荷兰计算机科学家,1972年图灵奖获得者。
Dijkstra 算法是一种高效的处理非负边权的 "单源最短路" 问题的算法,例如求出所有点距离源点 1 的距离。可以说 Dijkstra 是最重要的图论算法之一。
Dijkstra 算法利用了贪心和动态规划的思想,也有多个版本:朴素版、堆优化版。
这里直接讲解 Dijkstra 算法的堆优化版本 (priority_queue 优先队列实现,最常用,最高效)。朴素版相比堆优化版没有任何优势。
堆优化版本的时间复杂度为 O (nlogn),Dijkstra 算法中,图采用邻接表的方式存储。
2)代码以及相关细节详细解释
具体代码:
cpp
// 算法需要准备的东西:
int d[N];//d[i]表示距离源点的最短距离
bitset<N>vis;//表示某个点是否走过,按照dijkstra的贪心思想,第一次走到的时候得到的距离一定是最短距离,所以一个点
//不可能走第二次
struct Node
{
int x, w;//x表示点编号,w表示源点到x的最短距离
/*重载<运算符:
核心目的:适配 C++ 优先队列(priority_queue)的排序规则,实现小顶堆效果。
C++ 优先队列默认是大顶堆(按<运算符排序,堆顶是最大元素),而 Dijkstra 算法需要每次取出 "当前距离源点最近的顶点"(小顶堆,堆顶是最小元素),因此需要重载<运算符改变排序逻辑:
排序规则:先按w(距离)降序排列(w > u.w),若距离相等,则按顶点编号x升序排列(x < u.x,此为补充规则,不影响算法核心逻辑)。
效果:优先队列中,w越小的Node越靠近堆顶,每次pq.top()能快速取出当前距离源点最近的顶点。*/
bool operator<(const Node& u)const
{
return w == u.w ? x<u.x : w>u.w;//按照w降序,在优先队列中w最小的作为堆顶
}
};
priority_queue<Node>pq;
//本质:priority_queue 底层是堆(二叉堆),不是普通队列,不遵循 FIFO 规则;
//在 C++ 中,priority_queue(优先队列)的核心特性就是:
//每次弹出(pop() 操作)的元素必然是当前优先队列的堆顶元素,这是优先队列的默认行为,不会改变。
//C++ 优先队列的堆顶默认是大顶堆(最大值堆),即堆顶是队列中 "最大" 的元素;但堆顶的定义(是最大值还是最小值)并非固定,
//而是由我们定义的排序规则(比如Node结构体中重载的 < 运算符)决定。
void dijkstra(int st)
{
//初始化源点到i的距离为无穷
for (int i = 1; i <= n; i++)
{
d[i] = inf;
}
pq.push({ st,d[st]=0});//源点到源点的距离为0
while (pq.size())//只要队列不为空
{
int x = pq.top().x;
int w = pq.top().w;
pq.pop();//取出队头元素
//用c++17的绑定化语法:auto[x,w]=pq.top();pq.pop();
if (vis[x])continue;//如果走过,直接跳过
vis[x] = true;//标记为走过
for (const auto& [y, dw] : g[x])//x->y,边权为dw的边
{
if (d[x] + dw < d[y])//关键步骤,说明找到了一条更近的路
{
d[y] = d[x] + dw;
pq.push({y,d[y]});
}
}
/*在 C++17 之前,结构化绑定(structured binding)auto&[y,dw]的语法并不存在,
需要显式地访问结构体的成员。对于你的代码,可以这样修改:
for(const auto& edge : g[x]) // 遍历g[x]中的每个元素,用edge引用
{
ll y = edge.x; // 显式获取节点
ll dw = edge.w; // 显式获取权重
if(d[x] + dw < d[y])
{
d[y] = d[x] + dw;
pq.push({y, d[y]});
}
}*///*********非常重要!!!!!!!!!!!!!!!!!!!!!
}
}3)补充一个困扰我比较久的问题(虽然是个小问题):
图的存储里为什么用vector<int> g[N]而不是vector<int> g???
核心原因是图的结构特性决定了需要 "按顶点分组存储邻接边",直接说清楚:
- 先明确:这里的vector<int> g[N]是「邻接表」的存储方式
图的邻接表存储,本质是为每个顶点单独维护一个列表,记录该顶点的所有邻接顶点 / 边信息。
g[N]中的N:代表图的顶点数量(比如顶点编号是1~N)。
每个g[x](x是顶点编号):是一个vector,专门存储 "以x为起点的所有邻接边 / 顶点"。
- 为什么不能用vector<int> g?
如果只用一个vector<int> g(单个动态数组),无法区分 "哪些边属于哪个顶点"------ 所有顶点的邻接边会被混在一起存储,后续无法快速找到 "顶点x的邻接边"。
比如:
用g[N]:要找顶点3的邻接边,直接访问g[3]即可,时间复杂度 O (1) 定位。
用单个vector:需要遍历整个数组筛选 "属于顶点 3 的边",时间复杂度 O (m)(m 是边数),效率极低,完全无法支撑 Dijkstra 这类图算法的高效运行。
4)例题
蓝桥杯官网------蓝桥王国
问题描述
蓝桥王国一共有 N 个建筑和 M 条单向道路,每条道路都连接着两个建筑,每个建筑都有自己编号,分别为 1∼N 。(其中皇宫的编号为 1)
问:皇宫到每个建筑的最短路径是多少?
输入描述
输入第一行包含两个正整数 N,M。
第 2 到 M+1 行每行包含三个正整数 u,v,w,表示 u-->v 之间存在一条距离为 w 的路。
11≤N≤3×10^5,1≤m≤10^6,1≤ui,vi≤N,0≤wi≤10^9。
输出描述
输出仅一行,共 N 个数,分别表示从皇宫到编号为 1∼N 建筑的最短距离,两两之间用空格隔开。(如果无法到达则输出 −1)
输入输出样例
示例 1
输入:
3 3
1 2 1
1 3 5
2 3 2输出:
0 1 3代码详解:
cpp
#include <iostream>
#include<queue>
#include<vector>
#include<bitset>
using ll=long long;
using namespace std;
const ll N=3e5+9;
const ll inf=2e18;
ll d[N],n,m;
struct Node
{
//编号和到源节点的距离
ll x,w;
//重载>,编写排序规则
bool operator <(const Node& u)const
{
return w==u.w?x<u.x:w>u.w;
}
};
//vector<ll>g[N];注意vector存放的数据类型也是Node!
vector<Node>g[N];
void dijkstra(ll x)
{
//初始化
for(ll i=1;i<=n;i++) d[i]=inf;
bitset<N>vis;
priority_queue<Node>pq;
//源节点入队
pq.push({x,d[x]=0});
//弹出节点
while(pq.size())
{
ll x=pq.top().x;
ll w=pq.top().w;
pq.pop();//不要忘了出对
//判断x是否已经走过
if(vis[x]) continue;
vis[x]=true;
//拓展/松弛
for(const auto&[y,dw]:g[x])
{
if(d[x]+dw<d[y]) d[y]=d[x]+dw;
//将y入队
pq.push({y,d[y]});
}
}
}
int main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++)
{
ll u,v,w;cin>>u>>v>>w;
g[u].push_back({v,w});
}
dijkstra(1);
cout<<'\n';
for(int i=1;i<=n;i++)
{
cout<<(d[i]>=inf?-1:d[i])<<' ';
}
return 0;
}