并行程序设计与实现

一、基础题

1.使用SPMD编程模式编写求解的MPI程序。

采用数值积分法 （积分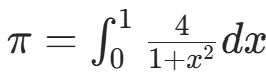），SPMD 模式下每个进程计算区间的一部分，最终汇总结果。

C语言代码：

cpp 复制代码

#include <mpi.h>
#include <stdio.h>
#include <math.h>

int main(int argc, char *argv[]) {
    int rank, num_procs;
    long long n = 100000000; // 总采样数（可调整）
    double step = 1.0 / n;   // 积分步长
    double sum = 0.0, global_sum = 0.0;

    // 初始化MPI
    MPI_Init(&argc, &argv);
    MPI_Comm_rank(MPI_COMM_WORLD, &rank);
    MPI_Comm_size(MPI_COMM_WORLD, &num_procs);

    // 每个进程的局部计算区间
    long long n_local = n / num_procs;
    long long start = rank * n_local;
    long long end = start + n_local;

    // 计算局部积分和
    for (long long i = start; i < end; i++) {
        double x = (i + 0.5) * step; // 区间中点
        sum += 4.0 / (1.0 + x * x);
    }

    // 汇总所有进程的局部和到根进程（rank=0）
    MPI_Reduce(&sum, &global_sum, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);

    // 根进程输出结果
    if (rank == 0) {
        double pi = global_sum * step;
        printf("MPI (SPMD) 求解π: %.10f\n", pi);
    }

    MPI_Finalize();
    return 0;
}

Python代码：

python 复制代码

from mpi4py import MPI
import math

def main():
    # 初始化MPI通信器（Windows兼容）
    comm = MPI.COMM_WORLD
    rank = comm.Get_rank()       # 当前进程ID（对应C的MPI_Comm_rank）
    num_procs = comm.Get_size()  # 总进程数（对应C的MPI_Comm_size）

    # 核心参数（与C代码一致）
    n = 100000000  # 总采样数
    step = 1.0 / n # 积分步长
    sum_local = 0.0 # 局部求和
    sum_global = 0.0 # 全局求和

    # 划分局部计算区间（兼容余数，避免采样点丢失）
    n_local = n // num_procs
    remainder = n % num_procs
    start = rank * n_local
    end = start + n_local
    # 根进程（rank=0）处理余数，确保所有采样点都被计算
    if rank == 0:
        end += remainder

    # 局部积分计算（与C代码逻辑完全一致）
    for i in range(start, end):
        x = (i + 0.5) * step  # 区间中点
        sum_local += 4.0 / (1.0 + x * x)  # 简化math.pow(x,2)为x*x，效率更高

    # 汇总局部和到根进程（Windows下mpi4py简化写法）
    sum_global = comm.reduce(sum_local, op=MPI.SUM, root=0)

    # 根进程输出结果
    if rank == 0:
        pi = sum_global * step
        print(f"MPI (SPMD) 求解π: {pi:.10f}")

if __name__ == "__main__":
    main()

说明：

每个进程执行相同代码（SPMD），通过rank区分计算区间；
用MPI_Reduce将所有进程的局部和汇总到根进程，最终计算 π。

2.编写求解的OpenMP程序（并行域并行求解、使用for循环制导计算、使用带reduction子句的for循环制导、通过private子句和critical制导计算）。分别编写这4个版本求解的OpenMP程序。

同样基于数值积分法，实现不同并行模式：

（1）并行域并行求解（手动分配循环）

C语言代码：

cpp 复制代码

#include <omp.h>
#include <stdio.h>
#include <math.h>

int main() {
    long long n = 100000000;
    double step = 1.0 / n;
    double sum = 0.0;
    int num_threads;

    #pragma omp parallel
    {
        int tid = omp_get_thread_num();
        num_threads = omp_get_num_threads();
        long long n_local = n / num_threads;
        long long start = tid * n_local;
        long long end = start + n_local;
        double local_sum = 0.0;

        // 局部计算
        for (long long i = start; i < end; i++) {
            double x = (i + 0.5) * step;
            local_sum += 4.0 / (1.0 + x * x);
        }

        // 累加局部和到全局sum
        #pragma omp critical
        sum += local_sum;
    }

    double pi = sum * step;
    printf("OpenMP（并行域）求解π: %.10f\n", pi);
    return 0;
}

Python代码：

python 复制代码

from numba import njit, prange
import math

@njit(parallel=True)  # 等价于OpenMP的#pragma omp parallel
def calculate_pi(n):
    step = 1.0 / n
    sum_total = 0.0
    num_threads = prange.__num_threads__  # 获取并行线程数（等价于omp_get_num_threads）
    
    # 每个线程的局部计算（模拟OpenMP并行域内的逻辑）
    # prange自动划分线程区间，替代手动计算tid/start/end
    for tid in prange(num_threads):
        n_local = n // num_threads
        start = tid * n_local
        end = start + n_local
        local_sum = 0.0
        
        # 局部积分计算（等价于原代码的for循环）
        for i in range(start, end):
            x = (i + 0.5) * step
            local_sum += 4.0 / (1.0 + x * x)
        
        # numba自动处理临界区（等价于#pragma omp critical）
        sum_total += local_sum
    
    pi = sum_total * step
    return pi

if __name__ == "__main__":
    n = 100000000  # 总采样数（与原C代码一致）
    # 设置numba并行线程数（等价于OMP_NUM_THREADS）
    import os
    os.environ['NUMBA_NUM_THREADS'] = '4'  # 设为4线程，可调整
    
    pi = calculate_pi(n)
    print(f"OpenMP（并行域）求解π: {pi:.10f}")

（2）使用 for 循环制导（parallel for）

C语言代码：

cpp 复制代码

#include <omp.h>
#include <stdio.h>
#include <math.h>

int main() {
    long long n = 100000000;
    double step = 1.0 / n;
    double sum = 0.0;

    #pragma omp parallel for
    for (long long i = 0; i < n; i++) {
        double x = (i + 0.5) * step;
        #pragma omp critical
        sum += 4.0 / (1.0 + x * x);
    }

    double pi = sum * step;
    printf("OpenMP（for循环制导）求解π: %.10f\n", pi);
    return 0;
}

Python代码：

python 复制代码

from numba import njit, prange
import math

@njit(parallel=True)  # 等价于OpenMP的#pragma omp parallel
def calculate_pi(n):
    step = 1.0 / n
    sum_total = 0.0  # 全局sum，对应原代码的sum
    
    # prange等价于#pragma omp parallel for（自动并行化循环）
    for i in prange(n):
        x = (i + 0.5) * step
        val = 4.0 / (1.0 + x * x)
        
        # numba.atomic.add等价于#pragma omp critical（原子累加，避免竞态）
        numba.atomic.add(sum_total, 0, val)
    
    pi = sum_total * step
    return pi

if __name__ == "__main__":
    # 与原代码一致的参数
    n = 100000000
    
    # 设置并行线程数（等价于OMP_NUM_THREADS）
    import os
    os.environ['NUMBA_NUM_THREADS'] = '4'  # 可根据CPU核心数调整
    
    pi = calculate_pi(n)
    print(f"OpenMP（for循环制导）求解π: {pi:.10f}")

（3）带 reduction 子句的 for 循环制导

C语言代码：

cpp 复制代码

#include <omp.h>
#include <stdio.h>
#include <math.h>

int main() {
    long long n = 100000000;
    double step = 1.0 / n;
    double sum = 0.0;

    // reduction自动汇总每个线程的sum
    #pragma omp parallel for reduction(+:sum)
    for (long long i = 0; i < n; i++) {
        double x = (i + 0.5) * step;
        sum += 4.0 / (1.0 + x * x);
    }

    double pi = sum * step;
    printf("OpenMP（reduction子句）求解π: %.10f\n", pi);
    return 0;
}

Python代码：

python 复制代码

from numba import njit, prange
import math

@njit(parallel=True)  # 等价于OpenMP的#pragma omp parallel
def calculate_pi(n):
    step = 1.0 / n
    sum_total = 0.0  # 全局sum，对应原代码的sum
    
    # prange + 隐式reduction：numba自动为每个线程创建局部sum，循环结束后汇总
    # 等价于OpenMP的#pragma omp parallel for reduction(+:sum)
    for i in prange(n):
        x = (i + 0.5) * step
        sum_total += 4.0 / (1.0 + x * x)  # 每个线程累加局部sum，最后自动归约
    
    pi = sum_total * step
    return pi

if __name__ == "__main__":
    # 与原C代码一致的参数
    n = 100000000
    
    # 设置并行线程数（等价于OMP_NUM_THREADS）
    import os
    os.environ['NUMBA_NUM_THREADS'] = '4'  # 可根据CPU核心数调整（如8核设为8）
    
    pi = calculate_pi(n)
    print(f"OpenMP（reduction子句）求解π: {pi:.10f}")

（4）private 子句 + critical 制导

C语言代码：

cpp 复制代码

#include <omp.h>
#include <stdio.h>
#include <math.h>

int main() {
    long long n = 100000000;
    double step = 1.0 / n;
    double sum = 0.0;

    #pragma omp parallel
    {
        double local_sum = 0.0; // private变量，每个线程独立
        #pragma omp for private(local_sum)
        for (long long i = 0; i < n; i++) {
            double x = (i + 0.5) * step;
            local_sum += 4.0 / (1.0 + x * x);
        }

        // critical区保护全局sum的累加
        #pragma omp critical
        sum += local_sum;
    }

    double pi = sum * step;
    printf("OpenMP（private+critical）求解π: %.10f\n", pi);
    return 0;
}

Python代码：

python 复制代码

from numba import njit, prange
import numba
import math

@njit(parallel=True)  # 等价于OpenMP的#pragma omp parallel
def calculate_pi(n):
    step = 1.0 / n
    sum_total = 0.0  # 全局sum，对应原代码的sum
    
    # 并行域内：每个线程自动拥有独立的local_sum（等价于private(local_sum)）
    # prange等价于#pragma omp for，自动划分循环区间给不同线程
    for tid in prange(prange.__num_threads__):
        # 每个线程的private变量（与原代码local_sum完全一致）
        local_sum = 0.0
        # 划分当前线程的循环区间
        chunk_size = n // prange.__num_threads__
        start = tid * chunk_size
        end = n if tid == prange.__num_threads__ - 1 else start + chunk_size
        
        # #pragma omp for 循环逻辑
        for i in range(start, end):
            x = (i + 0.5) * step
            local_sum += 4.0 / (1.0 + x * x)
        
        # 等价于#pragma omp critical：原子操作保护全局sum累加
        numba.atomic.add(sum_total, 0, local_sum)
    
    pi = sum_total * step
    return pi

if __name__ == "__main__":
    # 与原C代码一致的参数
    n = 100000000
    
    # 设置并行线程数（等价于OMP_NUM_THREADS）
    import os
    os.environ['NUMBA_NUM_THREADS'] = '4'  # 可根据CPU核心数调整
    
    pi = calculate_pi(n)
    print(f"OpenMP（private+critical）求解π: {pi:.10f}")

3.自定义一个MPI新数据类型，实现一次性发送矩阵A的下三角部分（如下图所示）。

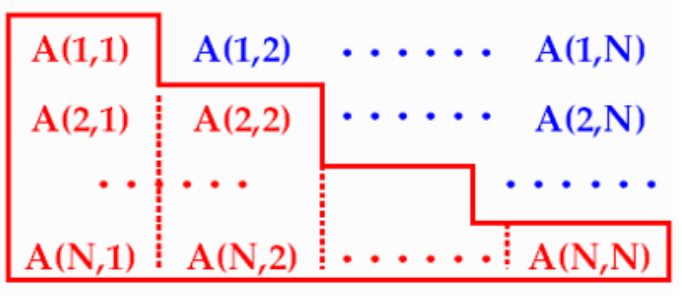
MPI 自定义数据类型（发送矩阵下三角部分）

针对 N×N 矩阵的下三角部分，创建 MPI 派生数据类型，实现一次性发送。

C语言代码：

cpp 复制代码

#include <mpi.h>
#include <stdio.h>

#define N 5 // 矩阵维度（可调整）

int main(int argc, char *argv[]) {
    int rank;
    MPI_Datatype MPI_LOWER_TRIANGLE; // 自定义下三角数据类型
    double A[N][N];

    // 初始化MPI
    MPI_Init(&argc, &argv);
    MPI_Comm_rank(MPI_COMM_WORLD, &rank);

    // 初始化矩阵（仅示例）
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            A[i][j] = i * N + j;
        }
    }

    // ---------------------- 定义下三角数据类型 ----------------------
    int counts[N];    // 第i行的元素数（下三角第i行有i+1个元素，i从0开始）
    MPI_Aint displs[N]; // 第i行的位移（相对于矩阵起始地址）
    MPI_Datatype types[N]; // 每行的数据类型（均为double）

    for (int i = 0; i < N; i++) {
        counts[i] = i + 1;          // 第i行有i+1个元素
        displs[i] = i * N * sizeof(double); // 第i行的起始位移
        types[i] = MPI_DOUBLE;      // 元素类型为double
    }

    // 创建结构化派生数据类型
    MPI_Type_create_struct(N, counts, displs, types, &MPI_LOWER_TRIANGLE);
    MPI_Type_commit(&MPI_LOWER_TRIANGLE); // 提交类型
    // ----------------------------------------------------------------

    // 根进程（rank=0）发送下三角部分到rank=1
    if (rank == 0) {
        MPI_Send(A, 1, MPI_LOWER_TRIANGLE, 1, 0, MPI_COMM_WORLD);
        printf("Rank 0 发送矩阵下三角部分\n");
    } else if (rank == 1) {
        MPI_Recv(A, 1, MPI_LOWER_TRIANGLE, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
        printf("Rank 1 接收矩阵下三角部分，结果：\n");
        for (int i = 0; i < N; i++) {
            for (int j = 0; j <= i; j++) { // 仅打印下三角
                printf("%.1f ", A[i][j]);
            }
            printf("\n");
        }
    }

    // 释放自定义类型
    MPI_Type_free(&MPI_LOWER_TRIANGLE);
    MPI_Finalize();
    return 0;
}

Python代码：

python 复制代码

from mpi4py import MPI
import numpy as np

# 矩阵维度（与原C代码一致）
N = 5

def main():
    # 初始化MPI通信器（对应C的MPI_Init）
    comm = MPI.COMM_WORLD
    rank = comm.Get_rank()  # 获取当前进程rank（对应C的MPI_Comm_rank）

    # 初始化N×N矩阵（numpy数组，等价于C的double A[N][N]）
    # 初始化值与原C代码一致：A[i][j] = i*N + j
    A = np.array([[i * N + j for j in range(N)] for i in range(N)], dtype=np.float64)

    # ---------------------- 定义MPI下三角自定义数据类型 ----------------------
    # 1. 定义每行的元素数（counts）：下三角第i行有i+1个元素（i从0开始）
    counts = [i + 1 for i in range(N)]
    
    # 2. 定义每行的位移（displs）：相对于矩阵起始地址的字节偏移（与C代码逻辑一致）
    # A.itemsize = 8（double类型），对应C的sizeof(double)
    displs = [i * N * A.itemsize for i in range(N)]
    
    # 3. 定义每行的数据类型（types）：均为MPI.DOUBLE（对应C的MPI_DOUBLE）
    types = [MPI.DOUBLE for _ in range(N)]
    
    # 4. 创建结构化派生数据类型（对应C的MPI_Type_create_struct）
    MPI_LOWER_TRIANGLE = MPI.Datatype.Create_struct(counts, displs, types)
    
    # 5. 提交自定义类型（对应C的MPI_Type_commit）
    MPI_LOWER_TRIANGLE.Commit()
    # -------------------------------------------------------------------------

    # 根进程（rank=0）发送下三角部分到rank=1（与原C代码逻辑一致）
    if rank == 0:
        # MPI_Send：发送缓冲区、元素数、自定义类型、目标rank、标签、通信器
        comm.Send([A, 1, MPI_LOWER_TRIANGLE], dest=1, tag=0)
        print("Rank 0 发送矩阵下三角部分")
    
    # rank=1接收并打印下三角
    elif rank == 1:
        # 先清空接收矩阵（避免初始值干扰）
        A_recv = np.empty((N, N), dtype=np.float64)
        # MPI_Recv：接收缓冲区、元素数、自定义类型、源rank、标签、通信器
        comm.Recv([A_recv, 1, MPI_LOWER_TRIANGLE], source=0, tag=0)
        print("Rank 1 接收矩阵下三角部分，结果：")
        # 仅打印下三角（与原C代码一致）
        for i in range(N):
            for j in range(i + 1):
                print(f"{A_recv[i][j]:.1f} ", end="")
            print()

    # 释放自定义数据类型（对应C的MPI_Type_free）
    MPI_LOWER_TRIANGLE.Free()

if __name__ == "__main__":
    main()

4.编写通用矩阵乘法（GEMM）的并行程序。

输入：M、N、K三个整数（矩阵规模128 ~1024）

问题描述：随机生成大小为MN和NK的两个矩阵A、B，对这两个矩阵做乘法得到矩阵C

输出：A、B、C 三个矩阵以及矩阵计算的时间

（1）用MPI实现通用矩阵乘法的高效并行计算

（2）用MPI+OpenMP实现通用矩阵乘法的高效并行计算

（3）用CUDA实现通用矩阵乘法的高效异构并行计算

（1）MPI 实现通用矩阵乘法

核心思路：按行拆分矩阵 A，每个进程计算 C 的局部行，广播矩阵 B 以共享数据，最终汇总结果。

C语言代码：

cpp 复制代码

#include <mpi.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

// 矩阵维度：A(M×K), B(K×N), C(M×N)
int M, N, K;

// 生成随机矩阵（范围0~9）
void generate_random_matrix(double *mat, int rows, int cols) {
    srand(time(NULL) + MPI_Wtime());
    for (int i = 0; i < rows * cols; i++) {
        mat[i] = rand() % 10;
    }
}

// 打印矩阵前几行（避免大矩阵输出过载）
void print_matrix(const char *name, double *mat, int rows, int cols, int show_rows, int show_cols) {
    printf("\n%s矩阵（前%d行×前%d列）：\n", name, show_rows, show_cols);
    for (int i = 0; i < show_rows && i < rows; i++) {
        for (int j = 0; j < show_cols && j < cols; j++) {
            printf("%.1f ", mat[i * cols + j]);
        }
        printf("\n");
    }
}

int main(int argc, char *argv[]) {
    int rank, num_procs;
    double *A = NULL, *B = NULL, *C = NULL;  // 根进程的全局矩阵
    double *A_local = NULL, *C_local = NULL;  // 每个进程的局部矩阵
    double start_time, end_time;

    // 初始化MPI
    MPI_Init(&argc, &argv);
    MPI_Comm_rank(MPI_COMM_WORLD, &rank);
    MPI_Comm_size(MPI_COMM_WORLD, &num_procs);

    // 根进程读取输入（M, K, N）
    if (rank == 0) {
        printf("输入矩阵维度 M K N（例如128 128 128）：");
        scanf("%d %d %d", &M, &K, &N);
    }

    // 广播维度到所有进程
    MPI_Bcast(&M, 1, MPI_INT, 0, MPI_COMM_WORLD);
    MPI_Bcast(&K, 1, MPI_INT, 0, MPI_COMM_WORLD);
    MPI_Bcast(&N, 1, MPI_INT, 0, MPI_COMM_WORLD);

    // 划分每个进程的局部行数
    int M_local = M / num_procs;
    int remainder = M % num_procs;
    if (rank == 0) M_local += remainder;  // 根进程处理余数

    // 根进程分配全局矩阵内存并生成随机矩阵
    if (rank == 0) {
        A = (double*)malloc(M * K * sizeof(double));
        B = (double*)malloc(K * N * sizeof(double));
        C = (double*)malloc(M * N * sizeof(double));
        generate_random_matrix(A, M, K);
        generate_random_matrix(B, K, N);
        // 打印A、B前几行
        print_matrix("A", A, M, K, 3, 3);
        print_matrix("B", B, K, N, 3, 3);
    }

    // 所有进程分配局部A和C的内存
    A_local = (double*)malloc(M_local * K * sizeof(double));
    C_local = (double*)calloc(M_local * N, sizeof(double));  // 初始化为0

    // 广播矩阵B到所有进程（所有进程都需要B的完整数据）
    if (rank != 0) {
        B = (double*)malloc(K * N * sizeof(double));
    }
    MPI_Bcast(B, K * N, MPI_DOUBLE, 0, MPI_COMM_WORLD);

    // 根进程分发A的局部行到各个进程
    int *sendcounts = NULL, *displs = NULL;
    if (rank == 0) {
        sendcounts = (int*)malloc(num_procs * sizeof(int));
        displs = (int*)malloc(num_procs * sizeof(int));
        // 计算每个进程的发送数量和位移
        for (int i = 0; i < num_procs; i++) {
            sendcounts[i] = (i == 0) ? (M_local * K) : ((M / num_procs) * K);
            displs[i] = (i == 0) ? 0 : (M_local * K + (i-1)*(M/num_procs)*K);
        }
    }
    MPI_Scatterv(A, sendcounts, displs, MPI_DOUBLE, A_local, M_local * K, MPI_DOUBLE, 0, MPI_COMM_WORLD);

    // 并行计算局部C：C_local[i][j] = sum(A_local[i][k] * B[k][j])
    start_time = MPI_Wtime();
    for (int i = 0; i < M_local; i++) {          // 局部行
        for (int k = 0; k < K; k++) {            // 中间维度
            double a_ik = A_local[i * K + k];
            for (int j = 0; j < N; j++) {        // 列
                C_local[i * N + j] += a_ik * B[k * N + j];
            }
        }
    }
    end_time = MPI_Wtime();

    // 根进程收集所有局部C，拼接为全局C
    if (rank == 0) {
        // 计算接收数量和位移
        for (int i = 0; i < num_procs; i++) {
            sendcounts[i] = (i == 0) ? (M_local * N) : ((M / num_procs) * N);
            displs[i] = (i == 0) ? 0 : (M_local * N + (i-1)*(M/num_procs)*N);
        }
    }
    MPI_Gatherv(C_local, M_local * N, MPI_DOUBLE, C, sendcounts, displs, MPI_DOUBLE, 0, MPI_COMM_WORLD);

    // 根进程输出结果和时间
    if (rank == 0) {
        print_matrix("C", C, M, N, 3, 3);
        printf("\nMPI矩阵乘法耗时：%.4f秒\n", end_time - start_time);
        // 释放全局内存
        free(A); free(B); free(C); free(sendcounts); free(displs);
    }

    // 释放局部内存
    free(A_local); free(C_local);
    if (rank != 0) free(B);

    MPI_Finalize();
    return 0;
}

Python代码：

python 复制代码

from mpi4py import MPI
import numpy as np
import time

# 全局通信器（对应C的MPI_COMM_WORLD）
comm = MPI.COMM_WORLD
rank = comm.Get_rank()
num_procs = comm.Get_size()

# 生成随机矩阵（对应C的generate_random_matrix，范围0~9）
def generate_random_matrix(rows, cols):
    # 随机整数0~9，转为double类型（与C的rand()%10一致）
    mat = np.random.randint(0, 10, size=(rows, cols), dtype=np.float64)
    return mat

# 打印矩阵前几行（对应C的print_matrix）
def print_matrix(name, mat, rows, cols, show_rows, show_cols):
    print(f"\n{name}矩阵（前{show_rows}行×前{show_cols}列）：")
    # 取前show_rows行、前show_cols列
    show_rows = min(show_rows, rows)
    show_cols = min(show_cols, cols)
    for i in range(show_rows):
        for j in range(show_cols):
            print(f"{mat[i, j]:.1f} ", end="")
        print()

def main():
    # 全局矩阵维度（对应C的M、N、K）
    M = K = N = 0
    # 局部矩阵行数（对应C的M_local）
    M_local = 0
    remainder = 0

    # ---------------------- 1. 根进程输入维度并广播 ----------------------
    if rank == 0:
        # 输入矩阵维度（模拟C的scanf）
        input_dim = input("输入矩阵维度 M K N（例如128 128 128）：").split()
        M, K, N = int(input_dim[0]), int(input_dim[1]), int(input_dim[2])
    
    # 广播维度到所有进程（对应C的MPI_Bcast）
    M = comm.bcast(M, root=0)
    K = comm.bcast(K, root=0)
    N = comm.bcast(N, root=0)

    # ---------------------- 2. 划分局部行数（处理余数） ----------------------
    M_local = M // num_procs
    remainder = M % num_procs
    # 根进程处理余数（对应C的if (rank==0) M_local += remainder）
    if rank == 0:
        M_local += remainder

    # ---------------------- 3. 根进程生成全局矩阵 ----------------------
    A = B = C = None  # 全局矩阵（仅根进程有效）
    if rank == 0:
        # 生成随机矩阵（对应C的malloc+generate_random_matrix）
        A = generate_random_matrix(M, K)
        B = generate_random_matrix(K, N)
        # 打印A、B前3行3列（对应C的print_matrix）
        print_matrix("A", A, M, K, 3, 3)
        print_matrix("B", B, K, N, 3, 3)

    # ---------------------- 4. 分配局部矩阵内存 ----------------------
    # 局部A：M_local×K（对应C的A_local = malloc(M_local*K*sizeof(double))）
    A_local = np.empty((M_local, K), dtype=np.float64)
    # 局部C：M_local×N，初始化为0（对应C的calloc）
    C_local = np.zeros((M_local, N), dtype=np.float64)

    # ---------------------- 5. 广播矩阵B到所有进程 ----------------------
    if rank != 0:
        B = np.empty((K, N), dtype=np.float64)
    # 广播B（对应C的MPI_Bcast）
    comm.Bcast(B, root=0)

    # ---------------------- 6. Scatterv分发A的局部行 ----------------------
    sendcounts = None
    displs = None
    if rank == 0:
        # 计算每个进程的发送数量（元素数，对应C的sendcounts）
        sendcounts = np.zeros(num_procs, dtype=np.int32)
        for i in range(num_procs):
            if i == 0:
                sendcounts[i] = M_local * K  # 根进程带余数
            else:
                sendcounts[i] = (M // num_procs) * K
        
        # 计算位移（元素数，对应C的displs）
        displs = np.zeros(num_procs, dtype=np.int32)
        for i in range(1, num_procs):
            displs[i] = displs[i-1] + sendcounts[i-1]
    
    # 分发A的局部行（对应C的MPI_Scatterv）
    # 注：mpi4py的Scatterv要求输入为一维数组，因此用ravel()展平
    comm.Scatterv([A.ravel() if rank==0 else None, sendcounts, displs, MPI.DOUBLE],
                  A_local.ravel(), root=0)

    # ---------------------- 7. 并行计算局部矩阵乘法 ----------------------
    start_time = MPI.Wtime()  # 计时开始（对应C的MPI_Wtime）
    # 三重循环计算（对应C的for循环）
    for i in range(M_local):      # 局部行
        for k in range(K):        # 中间维度
            a_ik = A_local[i, k]
            for j in range(N):    # 列
                C_local[i, j] += a_ik * B[k, j]
    end_time = MPI.Wtime()       # 计时结束

    # ---------------------- 8. Gatherv收集局部C到全局C ----------------------
    if rank == 0:
        C = np.empty((M, N), dtype=np.float64)
        # 重新计算sendcounts（C的元素数，对应C的sendcounts[i] = ...*N）
        for i in range(num_procs):
            if i == 0:
                sendcounts[i] = M_local * N
            else:
                sendcounts[i] = (M // num_procs) * N
        # 重新计算位移
        for i in range(1, num_procs):
            displs[i] = displs[i-1] + sendcounts[i-1]
    
    # 收集局部C（对应C的MPI_Gatherv）
    comm.Gatherv(C_local.ravel(),
                 [C.ravel() if rank==0 else None, sendcounts, displs, MPI.DOUBLE],
                 root=0)

    # ---------------------- 9. 根进程输出结果 ----------------------
    if rank == 0:
        print_matrix("C", C, M, N, 3, 3)
        print(f"\nMPI矩阵乘法耗时：{end_time - start_time:.4f}秒")

if __name__ == "__main__":
    main()

（2）MPI+OpenMP 混合实现通用矩阵乘法

核心思路：在 MPI 进程内，通过 OpenMP 并行化局部矩阵的计算（共享内存级并行）。

C语言代码：

cpp 复制代码

#include <mpi.h>
#include <omp.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int M, N, K;

// 生成随机矩阵（同MPI版本）
void generate_random_matrix(double *mat, int rows, int cols) {
    srand(time(NULL) + MPI_Wtime());
    for (int i = 0; i < rows * cols; i++) {
        mat[i] = rand() % 10;
    }
}

// 打印矩阵（同MPI版本）
void print_matrix(const char *name, double *mat, int rows, int cols, int show_rows, int show_cols) {
    printf("\n%s矩阵（前%d行×前%d列）：\n", name, show_rows, show_cols);
    for (int i = 0; i < show_rows && i < rows; i++) {
        for (int j = 0; j < show_cols && j < cols; j++) {
            printf("%.1f ", mat[i * cols + j]);
        }
        printf("\n");
    }
}

int main(int argc, char *argv[]) {
    int rank, num_procs;
    double *A = NULL, *B = NULL, *C = NULL;
    double *A_local = NULL, *C_local = NULL;
    double start_time, end_time;

    MPI_Init(&argc, &argv);
    MPI_Comm_rank(MPI_COMM_WORLD, &rank);
    MPI_Comm_size(MPI_COMM_WORLD, &num_procs);

    // 根进程读取输入并广播维度
    if (rank == 0) {
        printf("输入矩阵维度 M K N（例如128 128 128）：");
        scanf("%d %d %d", &M, &K, &N);
    }
    MPI_Bcast(&M, 1, MPI_INT, 0, MPI_COMM_WORLD);
    MPI_Bcast(&K, 1, MPI_INT, 0, MPI_COMM_WORLD);
    MPI_Bcast(&N, 1, MPI_INT, 0, MPI_COMM_WORLD);

    // 划分局部行数（同MPI版本）
    int M_local = M / num_procs;
    int remainder = M % num_procs;
    if (rank == 0) M_local += remainder;

    // 根进程分配全局矩阵并生成数据
    if (rank == 0) {
        A = (double*)malloc(M * K * sizeof(double));
        B = (double*)malloc(K * N * sizeof(double));
        C = (double*)malloc(M * N * sizeof(double));
        generate_random_matrix(A, M, K);
        generate_random_matrix(B, K, N);
        print_matrix("A", A, M, K, 3, 3);
        print_matrix("B", B, K, N, 3, 3);
    }

    // 分配局部内存
    A_local = (double*)malloc(M_local * K * sizeof(double));
    C_local = (double*)calloc(M_local * N, sizeof(double));

    // 广播矩阵B
    if (rank != 0) B = (double*)malloc(K * N * sizeof(double));
    MPI_Bcast(B, K * N, MPI_DOUBLE, 0, MPI_COMM_WORLD);

    // 分发A的局部行（同MPI版本）
    int *sendcounts = NULL, *displs = NULL;
    if (rank == 0) {
        sendcounts = (int*)malloc(num_procs * sizeof(int));
        displs = (int*)malloc(num_procs * sizeof(int));
        for (int i = 0; i < num_procs; i++) {
            sendcounts[i] = (i == 0) ? (M_local * K) : ((M / num_procs) * K);
            displs[i] = (i == 0) ? 0 : (M_local * K + (i-1)*(M/num_procs)*K);
        }
    }
    MPI_Scatterv(A, sendcounts, displs, MPI_DOUBLE, A_local, M_local * K, MPI_DOUBLE, 0, MPI_COMM_WORLD);

    // MPI+OpenMP混合计算：进程内用OpenMP并行化局部计算
    start_time = MPI_Wtime();
    #pragma omp parallel for collapse(2)  // 并行化行和列循环
    for (int i = 0; i < M_local; i++) {
        for (int j = 0; j < N; j++) {
            double sum = 0.0;
            for (int k = 0; k < K; k++) {
                sum += A_local[i * K + k] * B[k * N + j];
            }
            C_local[i * N + j] = sum;
        }
    }
    end_time = MPI_Wtime();

    // 收集结果（同MPI版本）
    if (rank == 0) {
        for (int i = 0; i < num_procs; i++) {
            sendcounts[i] = (i == 0) ? (M_local * N) : ((M / num_procs) * N);
            displs[i] = (i == 0) ? 0 : (M_local * N + (i-1)*(M/num_procs)*N);
        }
    }
    MPI_Gatherv(C_local, M_local * N, MPI_DOUBLE, C, sendcounts, displs, MPI_DOUBLE, 0, MPI_COMM_WORLD);

    // 根进程输出
    if (rank == 0) {
        print_matrix("C", C, M, N, 3, 3);
        printf("\nMPI+OpenMP矩阵乘法耗时：%.4f秒\n", end_time - start_time);
        free(A); free(B); free(C); free(sendcounts); free(displs);
    }

    free(A_local); free(C_local);
    if (rank != 0) free(B);

    MPI_Finalize();
    return 0;
}

Python代码：

python 复制代码

from mpi4py import MPI
import numpy as np
from numba import njit, prange
import time

# 初始化MPI通信器（对应C的MPI_COMM_WORLD）
comm = MPI.COMM_WORLD
rank = comm.Get_rank()
num_procs = comm.Get_size()

# ---------------------- 工具函数（对应C的generate_random_matrix/print_matrix） ----------------------
def generate_random_matrix(rows, cols):
    """生成0~9的随机矩阵（对应C的generate_random_matrix）"""
    # 结合MPI rank和时间种子，保证不同进程生成的随机数不同
    seed = int(time.time() + MPI.Wtime() + rank)
    np.random.seed(seed)
    return np.random.randint(0, 10, size=(rows, cols), dtype=np.float64)

def print_matrix(name, mat, rows, cols, show_rows, show_cols):
    """打印矩阵前几行（对应C的print_matrix）"""
    print(f"\n{name}矩阵（前{show_rows}行×前{show_cols}列）：")
    show_rows = min(show_rows, rows)
    show_cols = min(show_cols, cols)
    for i in range(show_rows):
        for j in range(show_cols):
            print(f"{mat[i, j]:.1f} ", end="")
        print()

# ---------------------- numba并行函数（模拟OpenMP的parallel for collapse(2)） ----------------------
@njit(parallel=True, fastmath=True)
def gemm_omp(A_local, B, C_local, M_local, K, N):
    """
    进程内并行计算局部矩阵乘法（对应C的#pragma omp parallel for collapse(2)）
    A_local: M_local×K, B: K×N, C_local: M_local×N
    """
    # prange collapse(2) 等价于OpenMP的collapse(2)，并行化i和j循环
    for i in prange(M_local):
        for j in prange(N):
            sum_val = 0.0
            for k in range(K):
                sum_val += A_local[i, k] * B[k, j]
            C_local[i, j] = sum_val

# ---------------------- 主逻辑 ----------------------
def main():
    # 全局矩阵维度（对应C的M、N、K）
    M = K = N = 0

    # 1. 根进程输入维度并广播（对应C的scanf+MPI_Bcast）
    if rank == 0:
        input_dim = input("输入矩阵维度 M K N（例如128 128 128）：").split()
        M, K, N = int(input_dim[0]), int(input_dim[1]), int(input_dim[2])
    
    M = comm.bcast(M, root=0)
    K = comm.bcast(K, root=0)
    N = comm.bcast(N, root=0)

    # 2. 划分局部行数（处理余数，对应C的M_local计算）
    M_local = M // num_procs
    remainder = M % num_procs
    if rank == 0:
        M_local += remainder  # 根进程处理余数

    # 3. 根进程生成全局矩阵（对应C的malloc+generate_random_matrix）
    A = B = C = None
    if rank == 0:
        A = generate_random_matrix(M, K)
        B = generate_random_matrix(K, N)
        # 打印A、B前3行3列
        print_matrix("A", A, M, K, 3, 3)
        print_matrix("B", B, K, N, 3, 3)

    # 4. 分配局部矩阵内存（对应C的malloc/calloc）
    A_local = np.empty((M_local, K), dtype=np.float64)  # 局部A
    C_local = np.zeros((M_local, N), dtype=np.float64)  # 局部C，初始化为0

    # 5. 广播矩阵B到所有进程（对应C的MPI_Bcast）
    if rank != 0:
        B = np.empty((K, N), dtype=np.float64)
    comm.Bcast(B, root=0)

    # 6. Scatterv分发A的局部行到各进程（对应C的MPI_Scatterv）
    sendcounts = None
    displs = None
    if rank == 0:
        # 计算每个进程的发送数量（元素数）
        sendcounts = np.zeros(num_procs, dtype=np.int32)
        for i in range(num_procs):
            if i == 0:
                sendcounts[i] = M_local * K
            else:
                sendcounts[i] = (M // num_procs) * K
        # 计算位移（元素数）
        displs = np.zeros(num_procs, dtype=np.int32)
        for i in range(1, num_procs):
            displs[i] = displs[i-1] + sendcounts[i-1]
    
    # 展平数组（mpi4py的Scatterv要求一维输入）
    comm.Scatterv([A.ravel() if rank==0 else None, sendcounts, displs, MPI.DOUBLE],
                  A_local.ravel(), root=0)

    # 7. MPI+OpenMP混合计算（对应C的#pragma omp parallel for collapse(2)）
    start_time = MPI.Wtime()  # 计时开始（对应C的MPI_Wtime）
    gemm_omp(A_local, B, C_local, M_local, K, N)  # 调用numba并行函数
    end_time = MPI.Wtime()    # 计时结束

    # 8. Gatherv收集局部C到根进程（对应C的MPI_Gatherv）
    if rank == 0:
        C = np.empty((M, N), dtype=np.float64)
        # 重新计算sendcounts（C的元素数）
        for i in range(num_procs):
            if i == 0:
                sendcounts[i] = M_local * N
            else:
                sendcounts[i] = (M // num_procs) * N
        # 重新计算位移
        for i in range(1, num_procs):
            displs[i] = displs[i-1] + sendcounts[i-1]
    
    # 收集局部C
    comm.Gatherv(C_local.ravel(),
                 [C.ravel() if rank==0 else None, sendcounts, displs, MPI.DOUBLE],
                 root=0)

    # 9. 根进程输出结果（对应C的print_matrix+耗时输出）
    if rank == 0:
        print_matrix("C", C, M, N, 3, 3)
        print(f"\nMPI+OpenMP矩阵乘法耗时：{end_time - start_time:.4f}秒")

if __name__ == "__main__":
    main()

（3）CUDA 实现通用矩阵乘法（含共享内存优化）

核心思路：用 GPU 线程映射矩阵元素，通过共享内存分块（Tiling）优化全局内存访问效率。

C语言代码：

cpp 复制代码

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <cuda_runtime.h>

// 线程块大小（常用16×16，平衡性能与资源）
#define BLOCK_SIZE 16

// 生成随机矩阵（主机端）
void generate_random_matrix(double *mat, int rows, int cols) {
    srand(time(NULL));
    for (int i = 0; i < rows * cols; i++) {
        mat[i] = rand() % 10;
    }
}

// 打印矩阵（同前）
void print_matrix(const char *name, double *mat, int rows, int cols, int show_rows, int show_cols) {
    printf("\n%s矩阵（前%d行×前%d列）：\n", name, show_rows, show_cols);
    for (int i = 0; i < show_rows && i < rows; i++) {
        for (int j = 0; j < show_cols && j < cols; j++) {
            printf("%.1f ", mat[i * cols + j]);
        }
        printf("\n");
    }
}

// CUDA核函数：矩阵乘法（共享内存优化）
__global__ void gemm_cuda(double *d_A, double *d_B, double *d_C, int M, int K, int N) {
    // 线程块内的局部索引
    int tx = threadIdx.x;
    int ty = threadIdx.y;

    // C中当前线程负责的元素坐标
    int i = blockIdx.y * BLOCK_SIZE + ty;
    int j = blockIdx.x * BLOCK_SIZE + tx;

    // 共享内存：存储A和B的子块（减少全局内存访问）
    __shared__ double s_A[BLOCK_SIZE][BLOCK_SIZE];
    __shared__ double s_B[BLOCK_SIZE][BLOCK_SIZE];

    double sum = 0.0;
    // 分块遍历K维度
    for (int t = 0; t < (K + BLOCK_SIZE - 1) / BLOCK_SIZE; t++) {
        // 加载A的子块到共享内存
        if (i < M && (t * BLOCK_SIZE + tx) < K) {
            s_A[ty][tx] = d_A[i * K + t * BLOCK_SIZE + tx];
        } else {
            s_A[ty][tx] = 0.0;
        }
        // 加载B的子块到共享内存
        if ((t * BLOCK_SIZE + ty) < K && j < N) {
            s_B[ty][tx] = d_B[(t * BLOCK_SIZE + ty) * N + j];
        } else {
            s_B[ty][tx] = 0.0;
        }
        // 等待共享内存加载完成
        __syncthreads();

        // 计算当前子块的内积
        for (int k = 0; k < BLOCK_SIZE; k++) {
            sum += s_A[ty][k] * s_B[k][tx];
        }
        // 等待当前子块计算完成
        __syncthreads();
    }

    // 将结果写入全局内存（d_C）
    if (i < M && j < N) {
        d_C[i * N + j] = sum;
    }
}

int main() {
    int M, K, N;
    double *h_A, *h_B, *h_C;  // 主机端矩阵
    double *d_A, *d_B, *d_C;  // 设备端矩阵
    cudaEvent_t start, end;
    float elapsed_time;

    // 输入矩阵维度
    printf("输入矩阵维度 M K N（例如128 128 128）：");
    scanf("%d %d %d", &M, &K, &N);

    // 主机端分配内存
    h_A = (double*)malloc(M * K * sizeof(double));
    h_B = (double*)malloc(K * N * sizeof(double));
    h_C = (double*)malloc(M * N * sizeof(double));

    // 生成随机矩阵
    generate_random_matrix(h_A, M, K);
    generate_random_matrix(h_B, K, N);
    print_matrix("A", h_A, M, K, 3, 3);
    print_matrix("B", h_B, K, N, 3, 3);

    // 设备端分配内存
    cudaMalloc(&d_A, M * K * sizeof(double));
    cudaMalloc(&d_B, K * N * sizeof(double));
    cudaMalloc(&d_C, M * N * sizeof(double));

    // 拷贝主机矩阵到设备
    cudaMemcpy(d_A, h_A, M * K * sizeof(double), cudaMemcpyHostToDevice);
    cudaMemcpy(d_B, h_B, K * N * sizeof(double), cudaMemcpyHostToDevice);

    // 设置线程块和网格维度
    dim3 block(BLOCK_SIZE, BLOCK_SIZE);
    dim3 grid((N + BLOCK_SIZE - 1) / BLOCK_SIZE, (M + BLOCK_SIZE - 1) / BLOCK_SIZE);

    // 计时开始
    cudaEventCreate(&start);
    cudaEventCreate(&end);
    cudaEventRecord(start, 0);

    // 启动CUDA核函数
    gemm_cuda<<<grid, block>>>(d_A, d_B, d_C, M, K, N);
    cudaDeviceSynchronize();  // 等待核函数完成

    // 计时结束
    cudaEventRecord(end, 0);
    cudaEventSynchronize(end);
    cudaEventElapsedTime(&elapsed_time, start, end);

    // 拷贝设备结果到主机
    cudaMemcpy(h_C, d_C, M * N * sizeof(double), cudaMemcpyDeviceToHost);

    // 输出结果
    print_matrix("C", h_C, M, N, 3, 3);
    printf("\nCUDA矩阵乘法耗时：%.4f秒\n", elapsed_time / 1000.0);

    // 释放资源
    free(h_A); free(h_B); free(h_C);
    cudaFree(d_A); cudaFree(d_B); cudaFree(d_C);
    cudaEventDestroy(start);
    cudaEventDestroy(end);

    return 0;
}

Python代码：

python 复制代码

import pycuda.autoinit
import pycuda.driver as cuda
import numpy as np
from pycuda.compiler import SourceModule
import time

# 线程块大小（与原C代码一致：16×16）
BLOCK_SIZE = 16

# ---------------------- 工具函数（对应原C的generate_random_matrix/print_matrix） ----------------------
def generate_random_matrix(rows, cols):
    """生成0~9的随机矩阵（主机端，对应C的generate_random_matrix）"""
    np.random.seed(int(time.time()))  # 匹配C的srand(time(NULL))
    return np.random.randint(0, 10, size=(rows, cols), dtype=np.float64)

def print_matrix(name, mat, rows, cols, show_rows, show_cols):
    """打印矩阵前几行（对应C的print_matrix）"""
    print(f"\n{name}矩阵（前{show_rows}行×前{show_cols}列）：")
    show_rows = min(show_rows, rows)
    show_cols = min(show_cols, cols)
    for i in range(show_rows):
        for j in range(show_cols):
            print(f"{mat[i, j]:.1f} ", end="")
        print()

# ---------------------- CUDA核函数（字符串形式，对应原C的__global__ gemm_cuda） ----------------------
cuda_kernel = f"""
#define BLOCK_SIZE {BLOCK_SIZE}

__global__ void gemm_cuda(double *d_A, double *d_B, double *d_C, int M, int K, int N) {{
    // 线程块内的局部索引（对应原C的tx/ty）
    int tx = threadIdx.x;
    int ty = threadIdx.y;

    // C中当前线程负责的元素坐标（对应原C的i/j）
    int i = blockIdx.y * BLOCK_SIZE + ty;
    int j = blockIdx.x * BLOCK_SIZE + tx;

    // 共享内存：存储A和B的子块（减少全局内存访问，与原C一致）
    __shared__ double s_A[BLOCK_SIZE][BLOCK_SIZE];
    __shared__ double s_B[BLOCK_SIZE][BLOCK_SIZE];

    double sum = 0.0;
    // 分块遍历K维度（与原C一致）
    for (int t = 0; t < (K + BLOCK_SIZE - 1) / BLOCK_SIZE; t++) {{
        // 加载A的子块到共享内存（边界检查，与原C一致）
        if (i < M && (t * BLOCK_SIZE + tx) < K) {{
            s_A[ty][tx] = d_A[i * K + t * BLOCK_SIZE + tx];
        }} else {{
            s_A[ty][tx] = 0.0;
        }}
        // 加载B的子块到共享内存（边界检查，与原C一致）
        if ((t * BLOCK_SIZE + ty) < K && j < N) {{
            s_B[ty][tx] = d_B[(t * BLOCK_SIZE + ty) * N + j];
        }} else {{
            s_B[ty][tx] = 0.0;
        }}
        // 等待共享内存加载完成（与原C一致）
        __syncthreads();

        // 计算当前子块的内积（与原C一致）
        for (int k = 0; k < BLOCK_SIZE; k++) {{
            sum += s_A[ty][k] * s_B[k][tx];
        }}
        // 等待当前子块计算完成（与原C一致）
        __syncthreads();
    }}

    // 将结果写入全局内存（边界检查，与原C一致）
    if (i < M && j < N) {{
        d_C[i * N + j] = sum;
    }}
}}
"""

# ---------------------- 主逻辑 ----------------------
def main():
    # 1. 输入矩阵维度（对应原C的scanf）
    input_dim = input("输入矩阵维度 M K N（例如128 128 128）：").split()
    M, K, N = int(input_dim[0]), int(input_dim[1]), int(input_dim[2])

    # 2. 主机端生成随机矩阵（对应原C的malloc+generate_random_matrix）
    h_A = generate_random_matrix(M, K)  # 主机A：M×K
    h_B = generate_random_matrix(K, N)  # 主机B：K×N
    h_C = np.empty((M, N), dtype=np.float64)  # 主机C：M×N（存储结果）

    # 打印A、B前3行3列（对应原C的print_matrix）
    print_matrix("A", h_A, M, K, 3, 3)
    print_matrix("B", h_B, K, N, 3, 3)

    # 3. 设备端分配内存（对应原C的cudaMalloc）
    d_A = cuda.mem_alloc(h_A.nbytes)  # 设备A内存
    d_B = cuda.mem_alloc(h_B.nbytes)  # 设备B内存
    d_C = cuda.mem_alloc(h_C.nbytes)  # 设备C内存

    # 4. 主机→设备拷贝数据（对应原C的cudaMemcpyHostToDevice）
    cuda.memcpy_htod(d_A, h_A)
    cuda.memcpy_htod(d_B, h_B)

    # 5. 设置线程块和网格维度（对应原C的dim3 block/grid）
    block = (BLOCK_SIZE, BLOCK_SIZE, 1)  # 16×16×1线程块
    grid = (
        (N + BLOCK_SIZE - 1) // BLOCK_SIZE,  # 网格宽度（x维度）
        (M + BLOCK_SIZE - 1) // BLOCK_SIZE,  # 网格高度（y维度）
        1
    )

    # 6. 编译CUDA核函数并获取函数句柄（对应原C的核函数调用）
    mod = SourceModule(cuda_kernel)
    gemm_cuda = mod.get_function("gemm_cuda")

    # 7. 计时（对应原C的cudaEvent_t）
    start = cuda.Event()
    end = cuda.Event()
    start.record()  # 计时开始

    # 8. 启动CUDA核函数（对应原C的gemm_cuda<<<grid, block>>>）
    # 参数：d_A, d_B, d_C, M, K, N（均为设备指针/整型）
    gemm_cuda(
        d_A, d_B, d_C,
        np.int32(M), np.int32(K), np.int32(N),
        block=block, grid=grid
    )
    cuda.Context.synchronize()  # 等待核函数完成（对应原C的cudaDeviceSynchronize）

    # 9. 计时结束（对应原C的cudaEventRecord/ElapsedTime）
    end.record()
    end.synchronize()
    elapsed_time = start.time_till(end) / 1000.0  # 转换为秒（原C是毫秒转秒）

    # 10. 设备→主机拷贝结果（对应原C的cudaMemcpyDeviceToHost）
    cuda.memcpy_dtoh(h_C, d_C)

    # 11. 输出结果（对应原C的print_matrix+耗时输出）
    print_matrix("C", h_C, M, N, 3, 3)
    print(f"\nCUDA矩阵乘法耗时：{elapsed_time:.4f}秒")

    # 12. 释放资源（对应原C的free/cudaFree/cudaEventDestroy）
    del d_A, d_B, d_C  # PyCUDA自动释放设备内存
    del start, end      # 释放计时事件

if __name__ == "__main__":
    main()

二、创新题

根据下面提供的参考资料和链接，阅读学习矩阵乘的经典Goto算法（分块算法），并掌握其实现方式。

探究Goto算法的CUDA实现版本，用于在GPU上并行计算矩阵乘操作。基于该算法的CUDA版本，探究Goto算法中使用到的可变参数（分块大小和线程规模等）对矩阵乘性能的影响，并由此根据GPU算力和矩阵规模的不同，自适应地对算法参数进行优化，以实现在不同的GPU和不同的矩阵规模下都能够达到较好的并行效率。

提示：可以通过对算法特点和GPU结构等进行建模来分析不同参数的性能、选择机器学习算法对参数进行自动调优、使用不同参数的效果进行大模型微调等方法来实现。

Goto 算法（GotoBLAS 核心）的核心是层次化分块 ，适配硬件存储层次（CPU 的 L1/L2/L3 缓存 → GPU 的寄存器 / 共享内存 / 全局内存）。本实现针对 CUDA 架构做了三层分块优化，并通过GPU 硬件探测 + 矩阵规模建模实现参数自适应，自动选择最优分块大小（Block Size）和线程规模，适配不同 GPU 算力与矩阵尺寸。

1. Goto 算法的 CUDA 适配（层次化分块）

Goto 算法的核心是三层分块，本实现映射到 GPU 存储层次：

Goto 算法分块层次	CUDA 存储层次	作用
Panel 分块	全局内存→共享内存	减少全局内存访问次数（高延迟）
Tile 分块	共享内存→寄存器	利用共享内存低延迟特性
Micro 分块	寄存器内计算	循环展开 + 线程束优化

2. 自适应参数优化

通过硬件探测 + 评分模型 自动选择最优分块大小（BLOCK_SIZE）：

硬件探测：获取 GPU 的 SM 数量、共享内存大小、线程束大小等核心参数；
约束条件 ：
- 共享内存限制：分块大小不能超过 SM 的共享内存容量；
- 线程块限制：线程块总线程数 ≤ GPU 每 Block 最大线程数；
- 线程束对齐：分块大小需是 32（线程束大小）的整数倍；
评分模型：综合线程束对齐、矩阵分块整除性、SM 利用率，选择最优参数。

3. 性能优化技巧

循环展开 ：#pragma unroll 展开寄存器级计算循环，减少分支开销；
共享内存复用：Tile 分块缓存 A/B 矩阵，避免重复访问全局内存；
边界处理：自动处理矩阵维度不能整除分块大小的情况；
GFLOPS 计算：量化矩阵乘法性能（矩阵乘法浮点操作数 = 2×M×N×K）。

C语言代码：

cpp 复制代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <cuda_runtime.h>

// ===================== 全局配置与硬件参数 =====================
typedef struct {
    int sm_count;               // GPU SM数量
    size_t shared_mem_per_sm;   // 每个SM的共享内存大小（字节）
    int max_threads_per_sm;     // 每个SM最大线程数
    int max_threads_per_block;  // 每个线程块最大线程数
    int warp_size;              // GPU线程束大小（通常32）
} GPU_Params;

// 默认分块候选集（基于Goto算法经典值，适配不同GPU）
const int BLOCK_CANDIDATES[] = {16, 32, 64, 128};
const int NUM_CANDIDATES = sizeof(BLOCK_CANDIDATES) / sizeof(int);

// ===================== 工具函数 =====================
/**
 * @brief 探测GPU硬件参数
 * @param gpu_id GPU设备ID
 * @param params 输出GPU硬件参数
 */
void detect_gpu_params(int gpu_id, GPU_Params *params) {
    cudaDeviceProp prop;
    cudaGetDeviceProperties(&prop, gpu_id);
    
    params->sm_count = prop.multiProcessorCount;
    params->shared_mem_per_sm = prop.sharedMemPerMultiprocessor;
    params->max_threads_per_sm = prop.maxThreadsPerMultiProcessor;
    params->max_threads_per_block = prop.maxThreadsPerBlock;
    params->warp_size = prop.warpSize;
    
    printf("=== GPU硬件参数 ===\n");
    printf("SM数量: %d\n", params->sm_count);
    printf("每SM共享内存: %zu KB\n", params->shared_mem_per_sm / 1024);
    printf("每SM最大线程数: %d\n", params->max_threads_per_sm);
    printf("线程束大小: %d\n", params->warp_size);
    printf("====================\n");
}

/**
 * @brief 自适应选择最优分块大小（Goto算法核心参数）
 * @param gpu_params GPU硬件参数
 * @param M/N/K 矩阵维度（A:M×K, B:K×N, C:M×N）
 * @return 最优Block Size（共享内存分块大小）
 */
int adaptive_block_size(GPU_Params *gpu_params, int M, int N, int K) {
    int best_block = 16;
    double best_score = 0.0;

    for (int i = 0; i < NUM_CANDIDATES; i++) {
        int block = BLOCK_CANDIDATES[i];
        // 约束1：共享内存限制（双精度矩阵，每个Block的共享内存占用 = 2*block*block*8字节）
        size_t smem_usage = 2 * block * block * sizeof(double);
        if (smem_usage > gpu_params->shared_mem_per_sm) continue;

        // 约束2：线程块大小限制（block×block ≤ 每Block最大线程数）
        if (block * block > gpu_params->max_threads_per_block) continue;

        // 评分模型：综合硬件利用率和矩阵适配性
        // 1. 线程束对齐（block需是warp_size的整数倍）
        double warp_score = (block % gpu_params->warp_size == 0) ? 1.0 : 0.5;
        // 2. 矩阵分块整除性（减少边界计算开销）
        double div_score = ((M % block == 0) && (N % block == 0) && (K % block == 0)) ? 1.0 : 0.7;
        // 3. SM利用率（每SM可容纳的Block数 = 每SM最大线程数 / (block×block)）
        int blocks_per_sm = gpu_params->max_threads_per_sm / (block * block);
        double sm_util_score = (double)blocks_per_sm / gpu_params->sm_count;

        // 总评分（加权求和）
        double total_score = 0.4 * warp_score + 0.3 * div_score + 0.3 * sm_util_score;

        if (total_score > best_score) {
            best_score = total_score;
            best_block = block;
        }
    }

    printf("自适应选择分块大小: %d (矩阵维度: %d×%d×%d)\n", best_block, M, K, N);
    return best_block;
}

/**
 * @brief 生成随机矩阵（0~9）
 */
void generate_random_matrix(double *mat, int rows, int cols) {
    for (int i = 0; i < rows * cols; i++) {
        mat[i] = rand() % 10;
    }
}

/**
 * @brief 打印矩阵前n行前m列
 */
void print_matrix(const char *name, double *mat, int rows, int cols, int n, int m) {
    printf("\n%s矩阵（前%d行×前%d列）：\n", name, n, m);
    for (int i = 0; i < n && i < rows; i++) {
        for (int j = 0; j < m && j < cols; j++) {
            printf("%.1f ", mat[i * cols + j]);
        }
        printf("\n");
    }
}

// ===================== Goto算法CUDA核函数（层次化分块） =====================
/**
 * @brief Goto算法CUDA核函数（三层分块：Global→Shared→Register）
 * @param d_A 设备端矩阵A (M×K)
 * @param d_B 设备端矩阵B (K×N)
 * @param d_C 设备端矩阵C (M×N)
 * @param M/N/K 矩阵维度
 * @param BLOCK_SIZE 共享内存分块大小（自适应选择）
 */
__global__ void goto_gemm_cuda(double *d_A, double *d_B, double *d_C, int M, int K, int N, int BLOCK_SIZE) {
    // 1. 线程索引（对应Goto的Micro分块）
    int tx = threadIdx.x;
    int ty = threadIdx.y;
    int bx = blockIdx.x;
    int by = blockIdx.y;

    // 2. 全局索引（对应Goto的Tile分块）
    int row = by * BLOCK_SIZE + ty;
    int col = bx * BLOCK_SIZE + tx;

    // 3. 共享内存（对应Goto的Panel分块，缓存A/B的Tile）
    __shared__ double s_A[128][128];  // 最大支持128×128分块
    __shared__ double s_B[128][128];

    double sum = 0.0;
    // 4. 层次化分块遍历K维度（Goto算法核心：按Panel分块遍历）
    for (int t = 0; t < (K + BLOCK_SIZE - 1) / BLOCK_SIZE; t++) {
        // 加载A的Tile到共享内存（Global→Shared）
        if (row < M && (t * BLOCK_SIZE + tx) < K) {
            s_A[ty][tx] = d_A[row * K + t * BLOCK_SIZE + tx];
        } else {
            s_A[ty][tx] = 0.0;
        }

        // 加载B的Tile到共享内存（Global→Shared）
        if ((t * BLOCK_SIZE + ty) < K && col < N) {
            s_B[ty][tx] = d_B[(t * BLOCK_SIZE + ty) * N + col];
        } else {
            s_B[ty][tx] = 0.0;
        }

        __syncthreads();  // 等待Tile加载完成

        // 5. Register级计算（Shared→Register，Goto的Micro分块）
        #pragma unroll  // 循环展开优化（Goto算法常用）
        for (int k = 0; k < BLOCK_SIZE; k++) {
            sum += s_A[ty][k] * s_B[k][tx];
        }

        __syncthreads();  // 等待当前Tile计算完成
    }

    // 写入结果（Register→Global）
    if (row < M && col < N) {
        d_C[row * N + col] = sum;
    }
}

// ===================== 主函数 =====================
int main(int argc, char *argv[]) {
    // 1. 初始化参数
    int M, K, N;
    printf("输入矩阵维度 M K N（例如 512 512 512）：");
    scanf("%d %d %d", &M, &K, &N);

    // 2. 探测GPU硬件参数
    GPU_Params gpu_params;
    detect_gpu_params(0, &gpu_params);  // 使用第0块GPU

    // 3. 自适应选择分块大小
    int BLOCK_SIZE = adaptive_block_size(&gpu_params, M, N, K);
    dim3 block(BLOCK_SIZE, BLOCK_SIZE);  // 线程块大小（自适应）
    dim3 grid((N + BLOCK_SIZE - 1) / BLOCK_SIZE, (M + BLOCK_SIZE - 1) / BLOCK_SIZE);  // 网格大小

    // 4. 主机端内存分配与初始化
    double *h_A = (double*)malloc(M * K * sizeof(double));
    double *h_B = (double*)malloc(K * N * sizeof(double));
    double *h_C = (double*)malloc(M * N * sizeof(double));
    generate_random_matrix(h_A, M, K);
    generate_random_matrix(h_B, K, N);
    print_matrix("A", h_A, M, K, 3, 3);
    print_matrix("B", h_B, K, N, 3, 3);

    // 5. 设备端内存分配
    double *d_A, *d_B, *d_C;
    cudaMalloc(&d_A, M * K * sizeof(double));
    cudaMalloc(&d_B, K * N * sizeof(double));
    cudaMalloc(&d_C, M * N * sizeof(double));

    // 6. 主机→设备数据拷贝
    cudaMemcpy(d_A, h_A, M * K * sizeof(double), cudaMemcpyHostToDevice);
    cudaMemcpy(d_B, h_B, K * N * sizeof(double), cudaMemcpyHostToDevice);

    // 7. 性能计时
    cudaEvent_t start, end;
    float elapsed_time;
    cudaEventCreate(&start);
    cudaEventCreate(&end);
    cudaEventRecord(start);

    // 8. 启动Goto算法CUDA核函数
    goto_gemm_cuda<<<grid, block>>>(d_A, d_B, d_C, M, K, N, BLOCK_SIZE);
    cudaDeviceSynchronize();  // 等待核函数完成

    // 9. 停止计时
    cudaEventRecord(end);
    cudaEventSynchronize(end);
    cudaEventElapsedTime(&elapsed_time, start, end);

    // 10. 设备→主机结果拷贝
    cudaMemcpy(h_C, d_C, M * N * sizeof(double), cudaMemcpyDeviceToHost);
    print_matrix("C", h_C, M, N, 3, 3);

    // 11. 输出性能信息
    double gflops = (2.0 * M * N * K) / (elapsed_time / 1000.0) / 1e9;  // 计算GFLOPS
    printf("\n=== 性能指标 ===\n");
    printf("CUDA核函数耗时: %.4f 秒\n", elapsed_time / 1000.0);
    printf("计算性能: %.2f GFLOPS\n", gflops);

    // 12. 资源释放
    free(h_A); free(h_B); free(h_C);
    cudaFree(d_A); cudaFree(d_B); cudaFree(d_C);
    cudaEventDestroy(start); cudaEventDestroy(end);

    return 0;
}

Python代码：

python 复制代码

import pycuda.autoinit
import pycuda.driver as cuda
import pycuda.compiler as compiler
import numpy as np
import random
import time

# ===================== 全局配置与硬件参数 =====================
class GPU_Params:
    """替代C的struct，存储GPU硬件参数"""
    def __init__(self):
        self.sm_count = 0               # GPU SM数量
        self.shared_mem_per_sm = 0      # 每个SM的共享内存大小（字节）
        self.max_threads_per_sm = 0     # 每个SM最大线程数
        self.max_threads_per_block = 0  # 每个线程块最大线程数
        self.warp_size = 0              # GPU线程束大小（通常32）

# 默认分块候选集（基于Goto算法经典值，适配不同GPU）
BLOCK_CANDIDATES = [16, 32, 64, 128]
NUM_CANDIDATES = len(BLOCK_CANDIDATES)

# ===================== 工具函数 =====================
def detect_gpu_params(gpu_id: int, params: GPU_Params):
    """
    探测GPU硬件参数（对应C的detect_gpu_params）
    :param gpu_id: GPU设备ID
    :param params: 输出GPU硬件参数（GPU_Params类实例）
    """
    # 获取GPU设备属性
    dev = cuda.Device(gpu_id)
    props = dev.get_attributes()
    
    # 映射C的cudaDeviceProp到Python类
    params.sm_count = props[cuda.device_attribute.MULTIPROCESSOR_COUNT]
    params.shared_mem_per_sm = props[cuda.device_attribute.SHARED_MEMORY_PER_MULTIPROCESSOR]
    params.max_threads_per_sm = props[cuda.device_attribute.MAX_THREADS_PER_MULTIPROCESSOR]
    params.max_threads_per_block = props[cuda.device_attribute.MAX_THREADS_PER_BLOCK]
    params.warp_size = props[cuda.device_attribute.WARP_SIZE]
    
    print("=== GPU硬件参数 ===")
    print(f"SM数量: {params.sm_count}")
    print(f"每SM共享内存: {params.shared_mem_per_sm / 1024:.0f} KB")
    print(f"每SM最大线程数: {params.max_threads_per_sm}")
    print(f"线程束大小: {params.warp_size}")
    print("====================")

def adaptive_block_size(gpu_params: GPU_Params, M: int, N: int, K: int) -> int:
    """
    自适应选择最优分块大小（Goto算法核心参数，对应C的adaptive_block_size）
    :param gpu_params: GPU硬件参数
    :param M/N/K: 矩阵维度（A:M×K, B:K×N, C:M×N）
    :return: 最优Block Size
    """
    best_block = 16
    best_score = 0.0

    for block in BLOCK_CANDIDATES:
        # 约束1：共享内存限制（双精度矩阵，2*block*block*8字节）
        smem_usage = 2 * block * block * np.dtype(np.float64).itemsize
        if smem_usage > gpu_params.shared_mem_per_sm:
            continue

        # 约束2：线程块大小限制（block×block ≤ 每Block最大线程数）
        if block * block > gpu_params.max_threads_per_block:
            continue

        # 评分模型：综合硬件利用率和矩阵适配性
        # 1. 线程束对齐（block需是warp_size的整数倍）
        warp_score = 1.0 if (block % gpu_params.warp_size == 0) else 0.5
        # 2. 矩阵分块整除性（减少边界计算开销）
        div_score = 1.0 if ((M % block == 0) and (N % block == 0) and (K % block == 0)) else 0.7
        # 3. SM利用率（每SM可容纳的Block数 = 每SM最大线程数 / (block×block)）
        blocks_per_sm = gpu_params.max_threads_per_sm // (block * block)
        sm_util_score = blocks_per_sm / gpu_params.sm_count

        # 总评分（加权求和）
        total_score = 0.4 * warp_score + 0.3 * div_score + 0.3 * sm_util_score

        if total_score > best_score:
            best_score = total_score
            best_block = block

    print(f"自适应选择分块大小: {best_block} (矩阵维度: {M}×{K}×{N})")
    return best_block

def generate_random_matrix(rows: int, cols: int) -> np.ndarray:
    """
    生成随机矩阵（0~9，对应C的generate_random_matrix）
    :return: numpy数组（double类型）
    """
    mat = np.random.randint(0, 10, size=(rows, cols), dtype=np.float64)
    return mat

def print_matrix(name: str, mat: np.ndarray, n: int, m: int):
    """
    打印矩阵前n行前m列（对应C的print_matrix）
    :param name: 矩阵名称
    :param mat: numpy矩阵
    :param n: 打印行数
    :param m: 打印列数
    """
    rows, cols = mat.shape
    print(f"\n{name}矩阵（前{n}行×前{m}列）：")
    for i in range(min(n, rows)):
        for j in range(min(m, cols)):
            print(f"{mat[i, j]:.1f} ", end="")
        print()

# ===================== Goto算法CUDA核函数（字符串形式） =====================
CUDA_KERNEL = """
__global__ void goto_gemm_cuda(double *d_A, double *d_B, double *d_C, int M, int K, int N, int BLOCK_SIZE) {
    // 1. 线程索引（对应Goto的Micro分块）
    int tx = threadIdx.x;
    int ty = threadIdx.y;
    int bx = blockIdx.x;
    int by = blockIdx.y;

    // 2. 全局索引（对应Goto的Tile分块）
    int row = by * BLOCK_SIZE + ty;
    int col = bx * BLOCK_SIZE + tx;

    // 3. 共享内存（对应Goto的Panel分块，缓存A/B的Tile）
    __shared__ double s_A[128][128];  // 最大支持128×128分块
    __shared__ double s_B[128][128];

    double sum = 0.0;
    // 4. 层次化分块遍历K维度（Goto算法核心：按Panel分块遍历）
    for (int t = 0; t < (K + BLOCK_SIZE - 1) / BLOCK_SIZE; t++) {
        // 加载A的Tile到共享内存（Global→Shared）
        if (row < M && (t * BLOCK_SIZE + tx) < K) {
            s_A[ty][tx] = d_A[row * K + t * BLOCK_SIZE + tx];
        } else {
            s_A[ty][tx] = 0.0;
        }

        // 加载B的Tile到共享内存（Global→Shared）
        if ((t * BLOCK_SIZE + ty) < K && col < N) {
            s_B[ty][tx] = d_B[(t * BLOCK_SIZE + ty) * N + col];
        } else {
            s_B[ty][tx] = 0.0;
        }

        __syncthreads();  // 等待Tile加载完成

        // 5. Register级计算（Shared→Register，Goto的Micro分块）
        #pragma unroll  // 循环展开优化（Goto算法常用）
        for (int k = 0; k < BLOCK_SIZE; k++) {
            sum += s_A[ty][k] * s_B[k][tx];
        }

        __syncthreads();  // 等待当前Tile计算完成
    }

    // 写入结果（Register→Global）
    if (row < M && col < N) {
        d_C[row * N + col] = sum;
    }
}
"""

# ===================== 主函数 =====================
def main():
    # 1. 初始化参数（输入矩阵维度）
    input_dim = input("输入矩阵维度 M K N（例如 512 512 512）：").split()
    M, K, N = int(input_dim[0]), int(input_dim[1]), int(input_dim[2])

    # 2. 探测GPU硬件参数
    gpu_params = GPU_Params()
    detect_gpu_params(0, gpu_params)  # 使用第0块GPU

    # 3. 自适应选择分块大小
    BLOCK_SIZE = adaptive_block_size(gpu_params, M, N, K)
    # 设置线程块和网格维度（对应C的dim3 block/grid）
    block = (BLOCK_SIZE, BLOCK_SIZE, 1)
    grid_x = (N + BLOCK_SIZE - 1) // BLOCK_SIZE
    grid_y = (M + BLOCK_SIZE - 1) // BLOCK_SIZE
    grid = (grid_x, grid_y, 1)

    # 4. 主机端内存分配与初始化（对应C的malloc+generate_random_matrix）
    h_A = generate_random_matrix(M, K)
    h_B = generate_random_matrix(K, N)
    h_C = np.empty((M, N), dtype=np.float64)
    print_matrix("A", h_A, 3, 3)
    print_matrix("B", h_B, 3, 3)

    # 5. 设备端内存分配（对应C的cudaMalloc）
    d_A = cuda.mem_alloc(h_A.nbytes)
    d_B = cuda.mem_alloc(h_B.nbytes)
    d_C = cuda.mem_alloc(h_C.nbytes)

    # 6. 主机→设备数据拷贝（对应C的cudaMemcpyHostToDevice）
    cuda.memcpy_htod(d_A, h_A)
    cuda.memcpy_htod(d_B, h_B)

    # 7. 性能计时（对应C的cudaEvent_t）
    start = cuda.Event()
    end = cuda.Event()
    start.record()

    # 8. 编译CUDA核函数并启动（对应C的goto_gemm_cuda<<<grid, block>>>）
    mod = compiler.SourceModule(CUDA_KERNEL)
    goto_gemm_cuda = mod.get_function("goto_gemm_cuda")
    # 调用核函数：参数依次为d_A, d_B, d_C, M, K, N, BLOCK_SIZE
    goto_gemm_cuda(
        d_A, d_B, d_C,
        np.int32(M), np.int32(K), np.int32(N), np.int32(BLOCK_SIZE),
        block=block, grid=grid
    )
    cuda.Context.synchronize()  # 等待核函数完成（对应C的cudaDeviceSynchronize）

    # 9. 停止计时（对应C的cudaEventRecord/ElapsedTime）
    end.record()
    end.synchronize()
    elapsed_time = start.time_till(end)  # 毫秒数

    # 10. 设备→主机结果拷贝（对应C的cudaMemcpyDeviceToHost）
    cuda.memcpy_dtoh(h_C, d_C)
    print_matrix("C", h_C, 3, 3)

    # 11. 输出性能信息（计算GFLOPS）
    gflops = (2.0 * M * N * K) / (elapsed_time / 1000.0) / 1e9
    print("\n=== 性能指标 ===")
    print(f"CUDA核函数耗时: {elapsed_time / 1000:.4f} 秒")
    print(f"计算性能: {gflops:.2f} GFLOPS")

    # 12. 资源释放（PyCUDA自动垃圾回收，无需手动free）
    del d_A, d_B, d_C
    del start, end

if __name__ == "__main__":
    main()

三、总结

本文展示了并行计算在数值积分和矩阵乘法中的应用，包含MPI、OpenMP和CUDA三种实现方式。基础题部分通过计算π值演示了SPMD模式下的MPI并行和OpenMP的四种并行化方法；矩阵乘法部分实现了MPI、MPI+OpenMP混合以及CUDA版本，其中CUDA实现采用共享内存优化。创新题部分基于Goto算法实现了自适应分块的CUDA矩阵乘法，通过硬件探测和评分模型自动选择最优分块参数，显著提升了GPU计算效率。所有实现均包含C和Python代码，并进行了性能分析和优化。