本文介绍了卷积神经网络(CNN)的基础知识,包括卷积、池化、拉平、批标准化等操作,示例解释了其内在原理,并举例了两个典型的卷积神经网络。理解神经网络的细节才能更好地指导AI大模型辅助构建满意的卷积神经网络模型。
本专栏的前述文章讨论了多层神经网络的多个重要问题,包括网络结构、参数优化、激活函数、损失函数、优化器和评价指标等。本文讨论神经网络中的卷积神经网络,它是神经网络中非常重要的一个类别,常用于图片、视频的处理中,也有用于文本处理的应用。
卷积神经网络(convolutional neural network, CNN)在提出之初被成功应用于手写字符图像识别,2012年的AlexNet网络在图像分类任务中取得成功,此后,卷积神经网络发展迅速,现在已经被广泛应用于图形、图像、语音识别等领域。
图片的像素数往往非常大,如果用上一章所讨论的多层全连接网络来处理,则参数数量将大到难以有效训练的地步。受猫脑研究的启发,卷积神经网络在多层全连接网络的基础上进行了改进,它在不减少层数的要求下有效提升了训练速度。卷积神经网络在多个研究领域都取得了成功,特别是在与图形有关的分类任务中。
1 卷积神经网络示例
本小节用示例来展示卷积神经网络在图像识别方面的优势,并将在随后的几个小节中逐一剖析其中的关键点。
本专栏的文章多次使用MNIST数据集来示例。通过采用交叉熵损失函数和adam优化算法,以及修改网络结构、增加训练轮数等措施,发现最高能达到0.983左右的识别率。
而较简单的卷积神经网络只需2轮训练就可以轻松达到98.82%的识别率,试验代码如代码 12-1所示。
自定义类CNN定义了两个方法:features和classifier,前者用于提取特征,后者用于分类。
在提取特征的features方法中,nn.Conv2d()添加的是所谓的卷积层,nn.MaxPool2d()添加的是所谓的池化层。卷积层和池化层是卷积神经网络的核心组成,它们和全连接层一起可以组合成很多层次的网络。
卷积神经网络还可以按需添加用来抑制过拟合的Dropout层、加快收敛和抑制梯度消散的批标准化BatchNormalization层、拉平多维数据的Flatten层等等。下文将对它们分别进行讨论。
值得注意的是,代码12-1所示的示例中,在数据预处理时,并没有将样本的标签值转变为独热编码,但是,类CNN定义的模型的输出却是独热编码的。这是因为所用的PyTorch的交叉熵损失函数CrossEntropyLoss()可以自动处理这种非独热编码的情况。
代码12-1 MNIST卷积神经网络应用示例
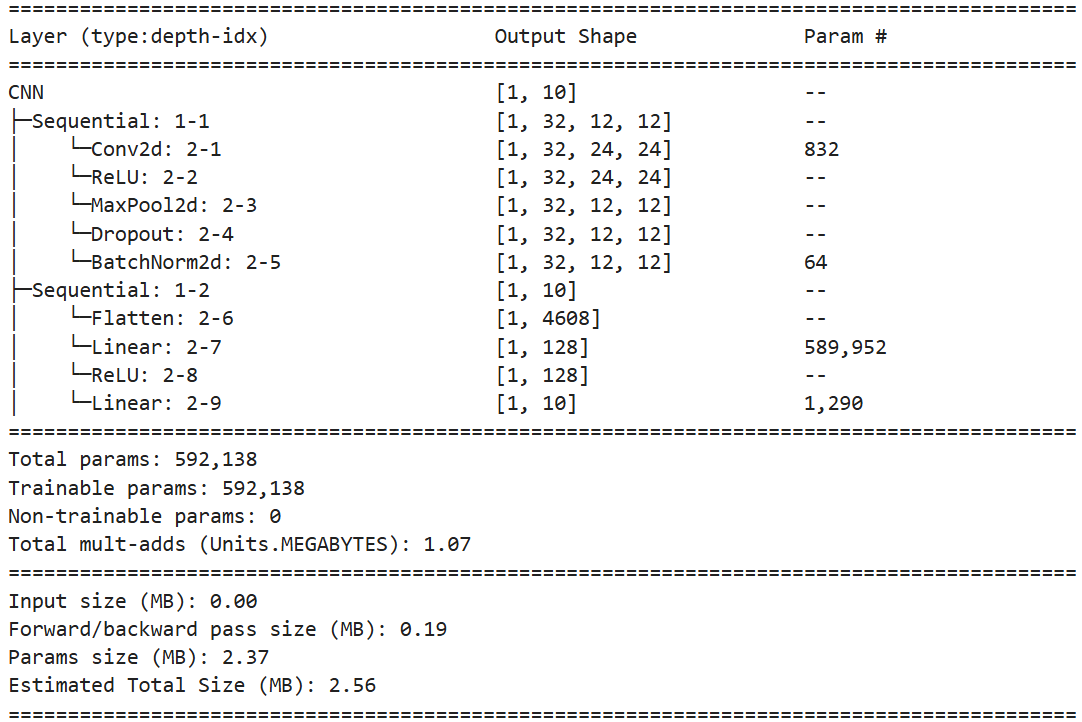
pythonimport torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import datetime from torchinfo import summary # 数据预处理和加载 transform = transforms.Compose([ transforms.ToTensor(), #transforms.Normalize((0.1307,), (0.3081,)) ]) train_dataset = datasets.MNIST('../data', train=True, download=True, transform=transform) test_dataset = datasets.MNIST('../data', train=False, transform=transform) print(train_dataset[0][0].shape) train_loader = DataLoader(train_dataset, batch_size=200, shuffle=True) test_loader = DataLoader(test_dataset, batch_size=200) # 定义CNN模型 class CNN(nn.Module): def __init__(self): super().__init__() self.features = nn.Sequential( nn.Conv2d(in_channels=1, out_channels=32, kernel_size=5), nn.ReLU(), nn.MaxPool2d(2), nn.Dropout(0.2), nn.BatchNorm2d(32) ) self.classifier = nn.Sequential( nn.Flatten(), nn.Linear(32*12*12, 128), nn.ReLU(), nn.Linear(128, 10) ) def forward(self, x): x = self.features(x) return self.classifier(x) model = CNN() print("模型结构:") summary(model, input_size=(1, 1, 28, 28))输出:
python# 定义损失函数和优化器 criterion = nn.CrossEntropyLoss() optimizer = optim.Adam(model.parameters()) # 训练函数 def train(model, train_loader, optimizer): model.train() for batch_idx, (data, target) in enumerate(train_loader): optimizer.zero_grad() output = model(data) loss = criterion(output, target) loss.backward() optimizer.step() # 测试函数 def test(model, test_loader): model.eval() correct = 0 with torch.no_grad(): for data, target in test_loader: output = model(data) pred = output.argmax(dim=1, keepdim=True) correct += pred.eq(target.view_as(pred)).sum().item() accuracy = 100. * correct / len(test_loader.dataset) print(f' 测试准确率: {accuracy:.2f}%') # 训练和测试 start_time = datetime.datetime.now() for epoch in range(1, 3): print("第", epoch, "轮训练", end="") train(model, train_loader, optimizer) test(model, test_loader) end_time = datetime.datetime.now() print(f"训练用时: {end_time - start_time}")输出:
第 1 轮训练 测试准确率: 98.37%
第 2 轮训练 测试准确率: 98.82%
训练用时: 0:00:58.143319
2 卷积层
代码12-1中定义的卷积神经网络模型的第一层是所谓的二维卷积层Conv2d,输入该卷积层的数据的维度是(1,28,28)。这与前文讨论的全连接层神经网络模型的输入不同,前文模型的输入是一维向量,该一维向量要么是经特征工程提取出来的特征,要么是被拉成一维的图像数据(见本专栏前面文章所用的多层全连接神经网络手写体数字识别示例)。而这里卷积层的输入是图片数据组成的多维数据。
在计算机中,一幅完整的图像是由像素点铺成,每个像素点包括由高(height)、宽(width)组成的位置信息和由红、绿、蓝组成的RGB三通道(channel)色彩信息。RGB三通道色彩是指每个像素点的颜色分别用代表红、绿、兰3原色的亮度数据来合成表示。RGB三通道色彩信息用一个三维的向量表示,如(0,0,0)表示黑色,(255,255,255)表示白色,(255,0,0)表示红色。
MNIST图片中,只有一种颜色,通常称灰色亮度。在PyTorch中,MNIST图片的维度是(1,28,28),前面1维表示像素点的灰色亮度值,称为单通道的,后面 2 维存储 28×2828 \times 2828×28 个像素点的坐标位置,因此称它单通道的 28×2828 \times 2828×28 数据。
从数学上来讲,卷积是一种积分变换。卷积在很多领域都得到了广泛的应用,如在统计学中它可用来做统计数据的加权滑动平均,在电子信号处理中通过将线性系统的输入与系统函数进行卷积得到系统输出,等等。在深度学习中,它用来做数据的卷积运算,在图像处理领域取得了非常好的效果。
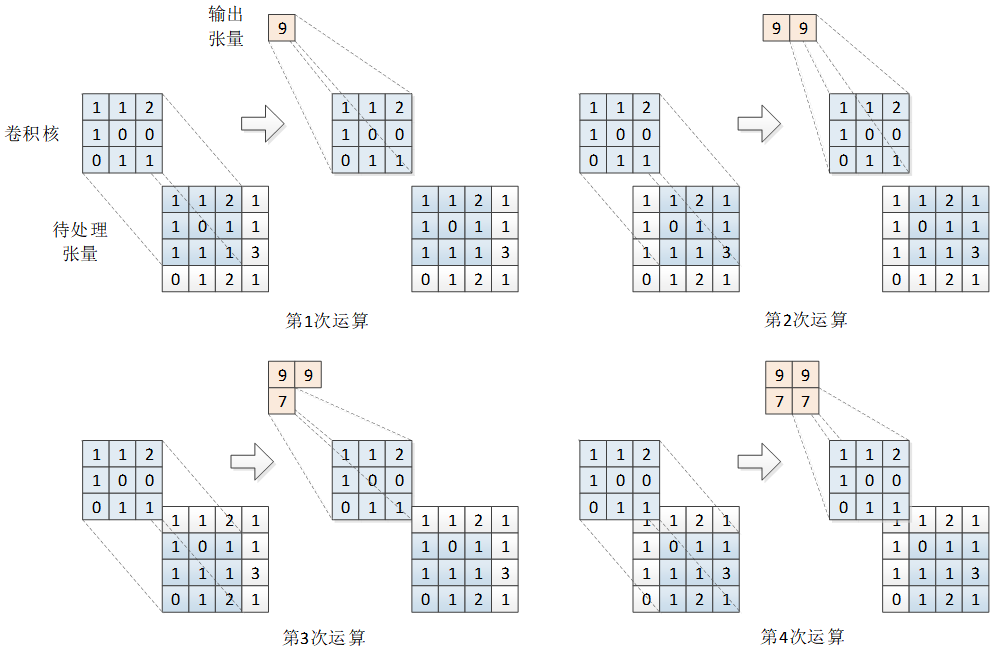
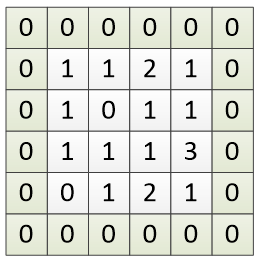
在单通道数据上的卷积运算示例如图 12-1 所示。单通道数据上的卷积运算包括待处理张量 III、卷积核 KKK 和输出张量 SSS 三个组成部分,它们的大小分别为 4×44 \times 44×4、3×33 \times 33×3 和 2×22 \times 22×2。
共进行了 4 次运算。
第 1 次运算先用卷积核的左上角去对准待处理张量的左上角,位置为 I(0,0)I(0,0)I(0,0),如图中深色部分。然后,将卷积核与对准部分的相应位置的值相乘再求和(可看作矩阵的点积运算):1×1+1×1+2×2+1×1+0×0+0×1+0×1+1×1+1×1=91 \times 1 + 1 \times 1 + 2 \times 2 + 1 \times 1 + 0 \times 0 + 0 \times 1 + 0 \times 1 + 1 \times 1 + 1 \times 1 = 91×1+1×1+2×2+1×1+0×0+0×1+0×1+1×1+1×1=9。所以,第 1 次运算的输出为 9,记为 S(0,0)=9S(0,0) = 9S(0,0)=9。
图12-1 卷积运算示例
第2次运算,将卷积核向右移动一步,卷积核的左上角对准待处理张量的位置为 I(0,1)I(0,1)I(0,1),再进行相应位置值的相乘求和,得到输出为 S(0,1)=9S(0,1) = 9S(0,1)=9。
第3次运算,因为卷积核已经到达最右边,因此下移一行,从最左边 I(1,0)I(1,0)I(1,0) 开始对准,然后再进行相应位置值的相乘求和,得到输出为 S(1,0)=7S(1,0) = 7S(1,0)=7。
第4次运算,将卷积核向右移动一步,到达 I(1,1)I(1,1)I(1,1),再与对准部分的相应位置的值相乘求和,得到输出为 S(1,1)=7S(1,1) = 7S(1,1)=7。
卷积核已经到达待处理张量的最右侧和最下侧,卷积运算结束。每次输出的结果也按移动位置排列,得到输出张量S=[9977]S = \begin{bmatrix} 9 & 9 \\ 7 & 7 \end{bmatrix}S=[9797]
记待处理的张量为 III,卷积核为 KKK,每一次卷积运算可表述为:
S(i,j)=(I∗K)(i,j)=∑m=1M∑n=1NI(i+m−1,j+n−1)K(m,n)(12-1) S(i,j) = (I * K)(i,j) = \sum_{m=1}^{M} \sum_{n=1}^{N} I(i + m - 1, j + n - 1)K(m,n)\tag{12-1} S(i,j)=(I∗K)(i,j)=m=1∑Mn=1∑NI(i+m−1,j+n−1)K(m,n)(12-1)
式中,I∗KI * KI∗K 表示卷积运算,MMM 和 NNN 分别表示卷积核的长度和宽度。i,ji,ji,j 是待处理张量的坐标位置,也是卷积核左上角对齐的位置。
按式12-1从上到下,从左到右依次卷积运算,可得输出张量 SSS。记待处理张量的长度和宽度为 PPP 和 QQQ,则输出张量 SSS 的长度 P′P'P′ 和 Q′Q'Q′ 宽度分别为:
P′=P−M+1Q′=Q−N+1(12-2) P' = P - M + 1\\ Q' = Q - N + 1\tag{12-2} P′=P−M+1Q′=Q−N+1(12-2)
代码12-1所示的示例,输入为 28×2828 \times 2828×28,卷积核为 5×55 \times 55×5,因此输出为 24×2424 \times 2424×24。
实际应用中,与神经元模型一样,卷积运算往往还要加1个阈值 θ\thetaθ,即:
S(i,j)=(I∗K)(i,j)=∑m=1M∑n=1NI(i+m,j+n)K(m,n)+θ(12-3) S(i,j) = (I * K)(i,j) = \sum_{m=1}^{M} \sum_{n=1}^{N} I(i + m, j + n)K(m,n) + \theta\tag{12-3} S(i,j)=(I∗K)(i,j)=m=1∑Mn=1∑NI(i+m,j+n)K(m,n)+θ(12-3)
卷积核 KKK 和阈值 θ\thetaθ 是要学习的参数。
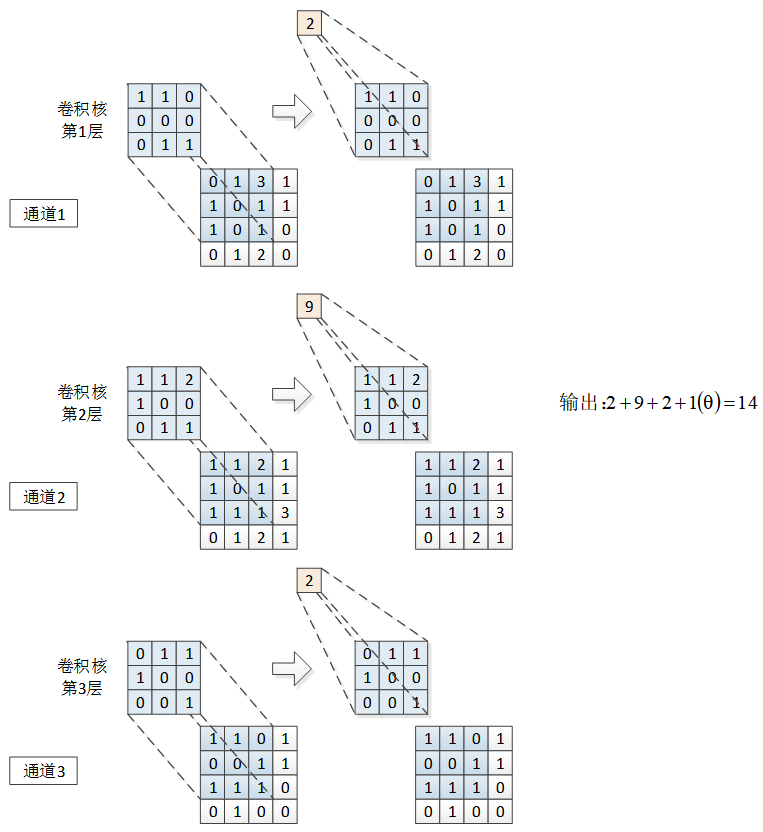
如果数据是多通道的,则卷积核也分为多层,每一层对应一个通道,各层参数不同。每层卷积核的操作与单通道上的卷积操作相同,最终输出是每层输出的和再加上阈值,如图12-2所示。因此,无论输入的张量有多少个通道,经过一个卷积核后的输出都是单层的。
图12-2 多通道卷积运算示例
从卷积运算的过程可见,卷积层的输出只与部分输入有关。虽然要扫描整个输入层,但卷积核的参数是一样的,这称为参数共享(parameter sharing)。参数共享大大减少了需要学习的参数的数量。
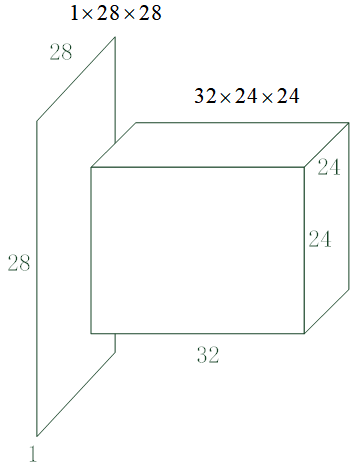
在卷积运算中,一般会设置多个卷积核。代码 12-1 所示的示例中设置了 323232 个卷积核,每个卷积核输出一层,因此该卷积层的输出是 323232 层的,也就是说将 1×28×281 \times 28 \times 281×28×28 的数据变成了 32×24×2432 \times 24 \times 2432×24×24 的。在画神经网络结构图时,一般用图 12-3 中的长方体来表示上述卷积运算,水平方向长度示意卷积核的数量。
图12-3 卷积层图示
再来算一下代码 12-1 示例中该卷积层的训练参数量。因为输入是单通道的,因此每个卷积核只有一层,它的参数为 5×5+1=265 \times 5 + 1 = 265×5+1=26,共 323232 个卷积核,因此训练参数为 26×32=83226 \times 32 = 83226×32=832 个。
如果待处理张量规模很大,可以将卷积核由依次移动改为跳跃移动,即一次移动两个或多个数据单元,称之为加大步长(strides)。加大步长可以减少计算量、加快训练速度。
为了提取到边缘的特征,可以在待处理张量的边缘填充 0 再进行卷积运算,称为零填充(zero-padding),如图 12-4 所示。填充也可以根据就近的值进行填充。
图12-4 边缘填充示例
边缘填充的另一个用途是在张量与卷积核不匹配时,通过填充使之匹配,从而卷积核能扫描到所有数据。
如采用图12-4所示的填充,在步长为1时,输出张量的长度和宽度都要加2。
来观察一下代码 12-1中二维卷积层的详细情况。该卷积层的输入通道数为1,输出通道数为32,因此设置了32个卷积核,每个卷积核大小为(5, 5)。
PyTorch的Conv2d操作的定义原型如代码12-2所示,其中,stride参数是设置步长,padding参数是设置填充方式。
代码12-2 PyTorch中Conv2d操作的原型
pythonCLASStorch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)
3 池化层和Flatten层
池化(pooling)层一般跟在卷积层之后,用于压缩数据和参数的数量。
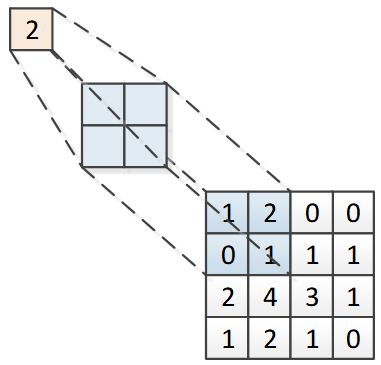
池化操作也叫下采样(sub-sampling),具体过程与卷积层基本相同,只不过池化层的卷积核只取对应位置的最大值或平均值,分别称为最大池化或平均池化。最大池化操作如图 12-5所示,将对应位置中的最大值输出,结果为2。如果是平均池化,则将对应位置中的所有值求平均值,得到输出1。池化层没有需要训练的参数。
代码12-5 最大池化操作示例
池化层的移动方式与卷积层不同,它是不重叠地移动,图12-5所示的池化操作,输出的张量的规模为 2×22 \times 22×2。代码12-1中features方法的池化层输出的张量为 32×12×1232 \times 12 \times 1232×12×12。
features方法中,在池化层后添加了抑止过拟合的dropout层。随后添加的是所谓的批标准化层,将在下一小节讨论。
用于分类的classifier方法中,第一行添加的是Flatten层。Flatten层很简单,只是将输入的多维数据拉成一维的,直观上可理解为将数据"压平"。随后添加了线性层、ReLU激活函数和另一个线性层。
PyTorch的线性层Linear需要显式设置输入参数个数,来看一下第一个Linear的输入参数个数是如何计算的。在卷积层中,每个卷积核将输入的 1×28×281 \times 28 \times 281×28×28 格式的数据转换成了 1×24×241 \times 24 \times 241×24×24格式的数据,因为有 323232 个卷积核,因此该卷积层的最终输出数据格式为 32×24×2432 \times 24 \times 2432×24×24。再经过一个核为 2×22 \times 22×2 的池化层,输出数据格式为 32×12×1232 \times 12 \times 1232×12×12。因此,它就是第一个Linear算子的输入参数。
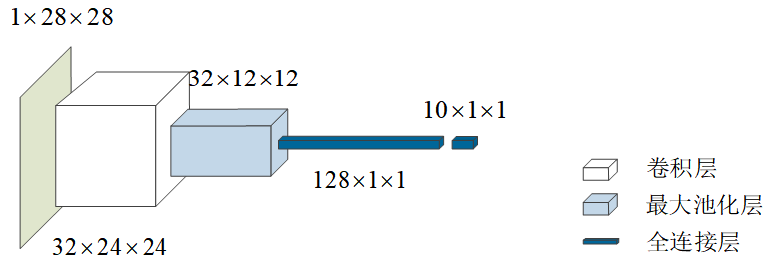
在画神经网络结构图时,可以用类似图12-3中的不同颜色的长方体来表示池化层和全连接层。除卷积层、池化层和全连接层(输入之前隐含Flatten层)之外,其他层不改变网络结构,因此,一般只用这三层来表示神经网络的结构。画出代码12-1所示示例的神经网络结构如图12-6所示。
图12-6 代码12-1示例的神经网络结构的画法
4 批标准化层
4.1 标准化
标准化(Z-Score)方法是针对对特征值概率分布敏感的算法而进行的调整特征值概率分布的方法。它是对某个特征进行的操作,先计算出该特征的均值和方差,然后对所有样本的该特征值减去均值并除以标准差。如样本的第 jjj 个特征 x(j)x^{(j)}x(j) 的均值估计为
meanx(j)=1m∑i=1mxi(j) \text{mean} x^{(j)} = \frac{1}{m} \sum_{i=1}^m x_i^{(j)} meanx(j)=m1i=1∑mxi(j)
方差估计为
varx(j)=1m∑i=1m(xi(j)−meanx(j))2 \text{var} x^{(j)} = \frac{1}{m} \sum_{i=1}^m \left( x_i^{(j)} - \text{mean} x^{(j)} \right)^2 varx(j)=m1i=1∑m(xi(j)−meanx(j))2
则 xi(j)x_i^{(j)}xi(j) 的标准化操作为:
Z−Score(xi(j))=xi(j)−meanx(j)varx(j) Z - \text{Score} \left( x_i^{(j)} \right) = \frac{x_i^{(j)} - \text{mean} x^{(j)}}{\sqrt{\text{var} x^{(j)}}} Z−Score(xi(j))=varx(j) xi(j)−meanx(j)
标准化操作的实质是将取值分布聚集在0附近,方差为1。实现标准化操作的有 sklearn.preprocessing 包的 scale() 函数和 StandardScaler 类。
4.2 批标准化
批标准化(Batch Normalization)可以抑制梯度消散,加速神经网络训练。
批标准化的提出者认为深度神经网络的训练之所以复杂,是因为在训练时每层的输入都随着前一层的参数的变化而变化。因此,在训练时,需要仔细调整步长和初始化参数来取得好的效果。
针对上述问题,在训练阶段,批标准化对每一层的批量输入数据 x\boldsymbol{x}x 进行标准化操作,使之尽量避免落入非线性激活函数的饱和区。具体来说就是使之均值为 000,方差为 111。记输入的某批某层的数据为向量 B={x1,x2,...,xm}\boldsymbol{B} = \{ \boldsymbol{x}_1, \boldsymbol{x}_2, ..., \boldsymbol{x}_m \}B={x1,x2,...,xm},其中 mmm 为每批输入训练样本的数量(代码12-1所示示例中为 200200200),对向量 B\boldsymbol{B}B 进行如下操作:
μB=1m∑i=1mxi \mu_B = \frac{1}{m} \sum_{i=1}^m \boldsymbol{x}_i μB=m1i=1∑mxi
σB2=1m∑i=1m(xi−μB)2 \sigma_B^2 = \frac{1}{m} \sum_{i=1}^m (\boldsymbol{x}_i - \mu_B)^2 σB2=m1i=1∑m(xi−μB)2
x^i=xi−μBσB2+ϵ \hat{\boldsymbol{x}}_i = \frac{\boldsymbol{x}_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} x^i=σB2+ϵ xi−μB
yi=γix^i+βi \boldsymbol{y}_i = \gamma_i \hat{\boldsymbol{x}}_i + \beta_i yi=γix^i+βi
其中,ϵ\epsilonϵ 为防止除 000 的很小的常数。前两步是计算所有数据的均值和方差,后两步是对每一项数据进行标准化和对标准化后的结果进行缩放和平移,其中的 γi\gamma_iγi 和 βi\beta_iβi 是要学习的参数。前两步中的 μB\mu_BμB 和 σB2\sigma_B^2σB2 是从输入数据中计算得到,是不需要训练的参数。
代码12-1所示示例中批标准化层的输入张量维度为 32×12×1232 \times 12 \times 1232×12×12,即输入张量的层数为 323232,即有 323232 个 γi\gamma_iγi、βi\beta_iβi、μB\mu_BμB 和 σB2\sigma_B^2σB2,因此,该层有 646464 个可训练参数和 646464 个不可训练参数。
2d批标准化层的实现函数为:torch.nn.BatchNorm2d(num_features=64),输入参数是通道数量。
5 典型卷积神经网络
在深度学习的发展过程中,出现了很多经典的卷积神经网络,它们对深度学习的学术研究和工业生产都起到了巨大的促进作用,如VGG、ResNet、Inception和DenseNet等,很多投入实用的卷积神经都是在它们的基础上进行改进的。初学者应从试验开始,通过阅读论文和实现代码(在PyTorch安装文件夹的torchvision的models文件夹中包含了很多经典的神经网络模型的源代码)来全面了解它们。下文简要讨论两个有代表性的卷积神经网络,它们都是卷积层、池化层、全连接层等的不同组合。
1.VGG-16,VGG-19
VGG-16是牛津大学的Visual Geometry Group在2015年发布的共16层的卷积神经网络,有约1.38亿个网络参数。该网络常被初学者用来学习和体验卷积神经网络。
VGG-16模型是针对ImageNet挑战赛设计的,该挑战赛的数据集为ILSVRC-2012图像分类数据集。ILSVRC-2012图像分类数据集的训练集有总共有1281167张图片,分为1000个类别,它的验证集有50000张图片样本,每个类别50个样本。
ILSVRC-2012图像分类数据集是2009年开始创建的ImageNet图像数据集的一部分。基于该图像数据集举办了具有很大影响力的ImageNet挑战赛,很多新模型就是在该挑战赛上发布的。
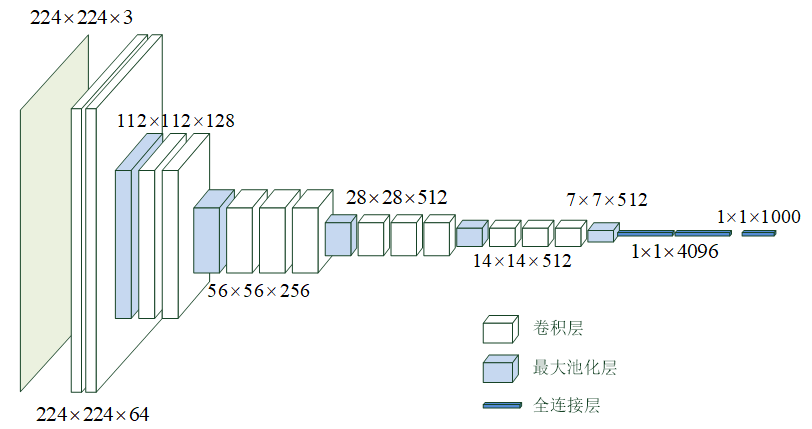
图12-7 VGG-16模型的网络结构
VGG-16 模型的网络结构如图 12-7 所示,从左侧输入大小为 224×224×3224 \times 224 \times 3224×224×3 的彩色图片,在右侧输出该图片的分类。
输入层之后,先是 2 个大小为 3×33 \times 33×3、卷积核数为 64、步长为 1、零填充的卷积层,此时的数据维度大小为 224×224×64224 \times 224 \times 64224×224×64,在水平方向被拉长了。
然后是 1 个大小为 2×22 \times 22×2 的最大池化层,将数据的维度降为 112×112×64112 \times 112 \times 64112×112×64,再经过 2 个大小为 3×33 \times 33×3、卷积核数为 128、步长为 1、零填充的卷积层,再一次在水平方向上被拉长,变为 112×112×128112 \times 112 \times 128112×112×128。
然后是 1 个大小为 2×22 \times 22×2 的最大池化层,和 3 个大小为 3×33 \times 33×3、卷积核数为 256、步长为 1、零填充的卷积层,数据维度变为 56×56×25656 \times 56 \times 25656×56×256。
然后是 1 个大小为 2×22 \times 22×2 的最大池化层,和 3 个大小为 3×33 \times 33×3、卷积核数为 512、步长为 1、零填充的卷积层,数据维度变为 28×28×51228 \times 28 \times 51228×28×512。
然后是 1 个大小为 2×22 \times 22×2 的最大池化层,和 3 个大小为 3×33 \times 33×3、卷积核数为 512、步长为 1、零填充的卷积层,数据维度变为 14×14×51214 \times 14 \times 51214×14×512。
然后是 1 个大小为 2×22 \times 22×2 的最大池化层,数据维度变为 7×7×5127 \times 7 \times 5127×7×512。
然后是 1 个 Flatten 层将数据拉平。
最后是 3 个全连接层,节点数分别为 4096、4096 和 1000。
除最后一层全连接层采用Softmax激活函数外,所有卷积层和全连接层都采用relu激活函数。
从上面网络结构可见,经过卷积层,通道数量不断增加,而经过池化层,数据的高度和宽度不断减少。
Visual Geometry Group后又发布了19层的VGG-19模型。
TensorFlow实现了VGG-16模型[ https://github.com/tensorflow/tensorflow/blob/master/tensorflow/python/keras/applications/vgg16.py\]和VGG-19模型,建议读者仔细阅读并分析。TensorFlow还提供了用ILSVRC-2012-CLS图像分类数据集预先训练好的VGG-16和VGG-19[ https://github.com/fchollet/deep-learning-models/releases/tag/v0.1\]模型,下面给出一个用预先训练好的模型来识别一幅图片(图 12-8)的例子。
图12-8 小狗图片
示例代码见代码12-3。示例中,提前将预训练模型下载放到相同目录中。文件imagenet_classes.txt是类别标签的英文注释。
代码12-3 VGG-19预训练模型应用
pythonimport torch import torchvision.models as models import torchvision.transforms as transforms from PIL import Image import matplotlib.pyplot as plt # 加载预训练模型 model = models.vgg19(pretrained=False) # 不自动下载模型 # 加载预先下载的模型,下载地址:https://download.pytorch.org/models/vgg19-dcbb9e9d.pth model.load_state_dict(torch.load('vgg19-dcbb9e9d.pth'), strict=False) # strict=False 允许部分权重不匹配 model.eval() # 设置为推理模式 # 图像预处理 preprocess = transforms.Compose([ transforms.Resize(256), transforms.CenterCrop(224), transforms.ToTensor(), transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]) ]) # 加载并预处理图像 image = Image.open('116.jpg') plt.figure(figsize=(8, 6)) plt.imshow(image) plt.axis('off') plt.title('Original Image') plt.show() input_tensor = preprocess(image) input_batch = input_tensor.unsqueeze(0) # 添加batch维度 # 使用GPU加速(如果可用) if torch.cuda.is_available(): input_batch = input_batch.to('cuda') model.to('cuda') # 执行推理 with torch.no_grad(): output = model(input_batch) # 获取预测结果 probabilities = torch.nn.functional.softmax(output[0], dim=0) # 加载ImageNet类别标签 with open('imagenet_classes.txt') as f: classes = [line.strip() for line in f.readlines()] # 输出top3预测结果 top3_prob, top3_catid = torch.topk(probabilities, 3) for i in range(top3_prob.size(0)): print(f"{classes[top3_catid[i]]}: {top3_prob[i].item()*100:.2f}%")输出:
toy poodle: 72.70%
miniature poodle: 25.55%
Lhasa: 0.37%
2.残差网络
随着网络层次的加深,训练集的损失函数可能会呈现出先下降再上升的现象,称为网络退化(degradation)现象。残差网络(ResNet)提出了抑制梯度消散、网络退化来加速训练收敛的方法,克服了层数多导致的收敛慢、甚至无法收敛的问题,使网络的层数得以增加。
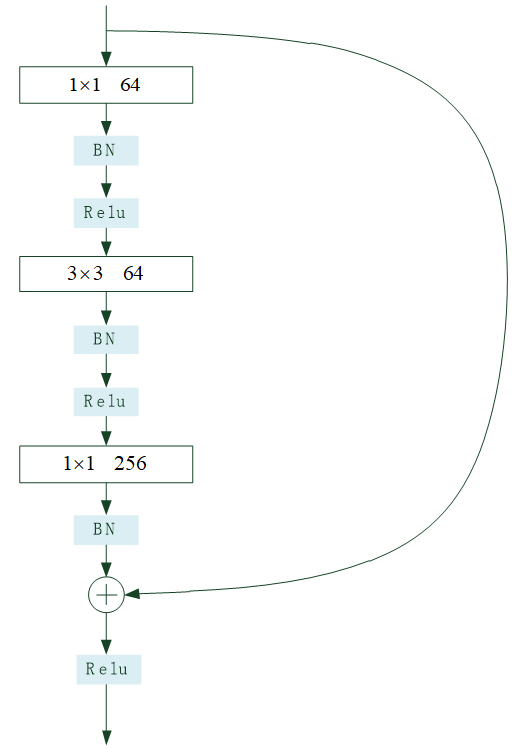
残差单元是残差网络的基本组成部分,它的特点是有一条跨层的短接。图12-9示例了一个残差单元。该单元有两条传递路径,除了常规的卷积、批标准化、激活处理路径外,还有一条跨层的直接传递路径。
图12-9 残差单元结构
残差网络一般要由很多残差单元首尾连接而成。残差网络的思想是通过跨层的短接,在误差反向传播时,去掉不变的主体部分,从而突出微小的变化,使得网络对误差更加敏感。通过短接还使得误差消散问题得到了较好的解决。试验结果证明残差网络具有良好的学习效果。
PyTorch中,实现残差单元的代码如代码12-4所示,该代码来自PyTorch安装目录下的torchvision目录下的models目录下的resnet.py文件,该目录有许多经典模型的实现代码,值得读者借鉴。代码12-4的倒数第3行实现了跨层短接。
代码12-4 残差单元的实现代码
pythonclass Bottleneck(nn.Module): # Bottleneck in torchvision places the stride for downsampling at 3x3 convolution(self.conv2) # while original implementation places the stride at the first 1x1 convolution(self.conv1) # according to "Deep residual learning for image recognition" https://arxiv.org/abs/1512.03385. # This variant is also known as ResNet V1.5 and improves accuracy according to # https://ngc.nvidia.com/catalog/model-scripts/nvidia:resnet_50_v1_5_for_pytorch. expansion: int = 4 def __init__( self, inplanes: int, planes: int, stride: int = 1, downsample: Optional[nn.Module] = None, groups: int = 1, base_width: int = 64, dilation: int = 1, norm_layer: Optional[Callable[..., nn.Module]] = None, ) -> None: super().__init__() if norm_layer is None: norm_layer = nn.BatchNorm2d width = int(planes * (base_width / 64.0)) * groups # Both self.conv2 and self.downsample layers downsample the input when stride != 1 self.conv1 = conv1x1(inplanes, width) self.bn1 = norm_layer(width) self.conv2 = conv3x3(width, width, stride, groups, dilation) self.bn2 = norm_layer(width) self.conv3 = conv1x1(width, planes * self.expansion) self.bn3 = norm_layer(planes * self.expansion) self.relu = nn.ReLU(inplace=True) self.downsample = downsample self.stride = stride def forward(self, x: Tensor) -> Tensor: identity = x out = self.conv1(x) out = self.bn1(out) out = self.relu(out) out = self.conv2(out) out = self.bn2(out) out = self.relu(out) out = self.conv3(out) out = self.bn3(out) if self.downsample is not None: identity = self.downsample(x) out += identity out = self.relu(out) return out