深度学习网络笔记Ⅰ(CNN)

0.概念区分

python 复制代码

"""
人工智能（AI） 
├─ 机器学习（ML）：AI的核心分支，让机器通过数据「自主学习规律」（无需手动编写规则）
│  ├─ 传统机器学习算法（非神经网络类）：如决策树、SVM、逻辑回归、KNN等（依赖人工特征工程）
│  └─ 神经网络（NN/ANN）：机器学习的一个子集，模拟人脑神经元连接结构（由输入层、隐藏层、输出层组成）
│     └─ 深度学习（DL）：神经网络的「进阶形态」（核心是「深度」+「端到端学习」）
│        ├─ 深度学习网络类型：CNN（卷积神经网络）、RNN/LSTM（循环神经网络）、Transformer（注意力机制网络）、GAN（生成对抗网络）等
│        └─ 深度学习算法：对应网络的「学习逻辑」（如反向传播、梯度下降、Adam优化、交叉熵损失等）
└─ 非机器学习类AI：如规则引擎、专家系统（依赖人工编写固定规则，无自主学习能力）
"""

维度	神经网络（传统）	深度学习网络
隐藏层数量	0 或 1 层	≥2 层（深度可至数十 / 上百层）
特征提取方式	依赖人工设计特征（如 SIFT、HOG）	自动从数据中学习多层次特征
计算复杂度	低，可 CPU 运行	高，依赖 GPU/TPU 加速
适用任务	简单线性 / 非线性分类回归	复杂任务（图像识别、NLP、语音）

网络学习本质：

所有可训练的深度学习网络，不管结构多复杂、应用场景多不同，本质都是 "为了优化参数（W+b），找到输入数据到任务目标的'更优映射关系'"------ 网络结构只是实现这个目标的 "适配性工具"。

1.神经网络的四维分类

分类维度	核心逻辑	典型类别
1. 数据类型适配	网络结构是为了适配「不同类型的输入数据」（解决 "数据怎么喂进去" 的问题）	- 网格数据（图像 / 语音）：CNN（卷积神经网络） - 序列数据（文本 / 时序）：RNN/LSTM/GRU/Transformer- 非结构化数据（任意维度）：MLP（多层感知机）
2. 网络结构特征	核心层的设计方式（解决 "特征怎么提" 的问题）	- 全连接型：MLP（所有神经元两两连接） - 局部连接 + 权值共享：CNN（卷积层） - 时序依赖型：RNN（循环连接） - 注意力机制型：Transformer（自注意力层）
3. 学习方式	模型如何获取标签信息（解决 "怎么学" 的问题）	- 监督学习：CNN（图像分类）、RNN（文本翻译）、Transformer（BERT）。 - 无监督学习：AutoEncoder（自编码器）、GAN（生成对抗网络） - 半监督 / 弱监督：带伪标签的 CNN、对比学习模型
4. 任务目标	模型要解决的具体问题（解决 "学了干嘛" 的问题）	- 分类任务：CNN（图像分类）、MLP（简单分类） - 回归任务：MLP（房价预测）、CNN（图像分割的像素回归） - 生成任务：GAN（图像生成）、VAE（ variational 自编码器） - 序列任务：RNN（文本生成）、Transformer（机器翻译）

本质：每一个神经网络可以按下面四个维度进行交织定义。

例：CNN网络：网格数据+ 局部感知，权值共享**+监督学习+**回归任务。

CNN的核心定位：适配网格数据的局部连接权值共享的监督学习网络，用于解决回归问题。

2.卷积神经网络CNN

1.基础知识储备

CNN网络结构的本质：利用 "局部感受野 + 参数共享" 机制，通过多层卷积(线性变换)与激活函数(非线性变换），自动完成从低级的几何特征逐步到高级的语义特征的分层提取，最终获取其映射关系，也就是参数（权重 W+ 偏置b）优化模型。

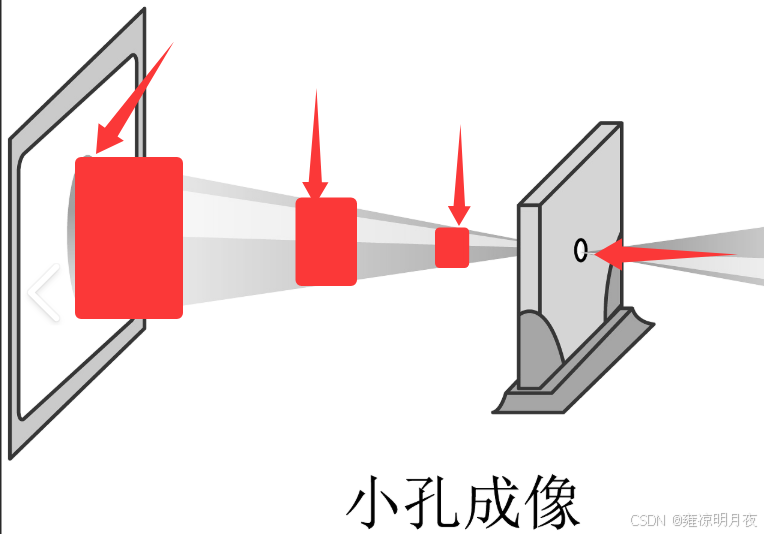
**感受野：**本质类似下图中的小孔成像，当前 feature map 上的一个点能代表原始区域的区域大小。如下图从右到左，每一层feature map的每个点的感受野变换1x1 -> 3x3 ->5x5->7x7.简单来讲就是后面的卷积层上的像素点相当于前面卷积层的实际区域大小。

全局平均池化(GAP)：本质是 "空间维度的压缩"：对每个通道的所有像素点取平均值，把 H×W×N 的特征图，压缩成 1×1×N 的向量。

举例：

输入特征图：14×14×10（10 个通道，每个通道 14×14 像素）

对每个通道的 14×14=196 个像素取平均，得到 10 个数值（每个通道 1 个平均值）。

输出向量：1×1×10（和全连接层的输出 shape 完全一致，对应 10 个类别的得分）。

⭐1x1卷积的作用：

1.1x1卷积不会改变其特征图的H，W。

2.1x1卷积可以用来更改特征图的数量进一步减少其W数量并且其网路结构变深了****，也就是仅通过更改output_channel来达到更改shape的作用。

3.网路深度变深->增加了非线性，进一步增加了网络表达能力。

4.空间信息的沟通和融合也增加。

5.1x1卷积结合全局平均池化(GAP)，能够起到全连接的作用。（ 且参数更少，效果更优）

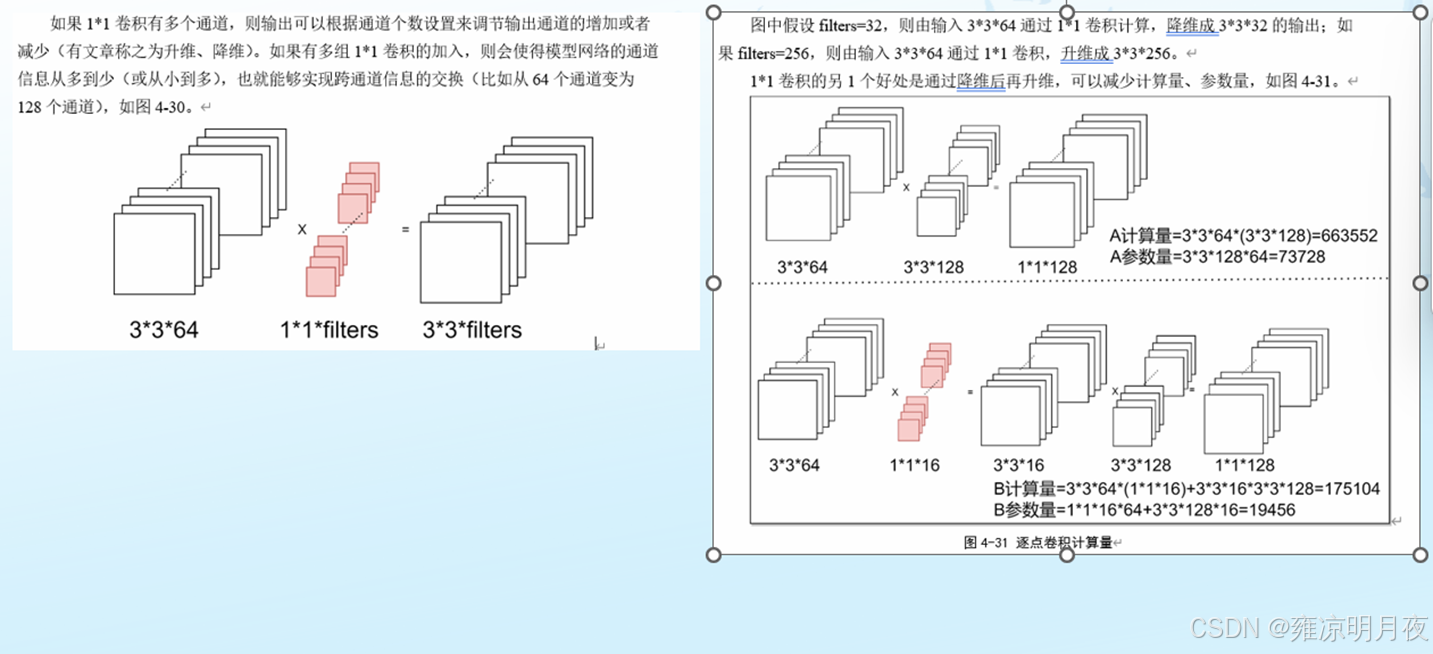
⭐详解上述第5点 ：1x1 卷积的 "通道维度线性变换" 对应非最后一层全连接层的核心功能，1x1 卷积 + GAP 的 "通道变换 + 全局压缩" 对应最后一层全连接层的核心功能，二者是 "功能等效"。

解释：类似于VGG等网络结构中有多个FC层, 已知： FC层=线性变换+非线性变换。

我们可以做两个优化:

1.针对最后一个FC_end也就是功能映射层用 1x1卷积+GPA 替换 FC_end。

2.针对FC_end之前的FC中的线性变化我们可以用1x1卷积来替代。

根本目的：极大的减少了其W数量和计算量。

替代方式	参数减少	空间信息保留	适用场景
1×1 卷积替代中间 FC	FC1: 从 102M→2.1M（减少 98%）	完全保留 7×7 空间结构	所有中间特征变换层
1×1+GAP 替代最后 FC	FC3: 4.1M 参数，数量相同但更高效	全局特征（消除空间）	最终分类 / 回归层

以VGG网络结构为例子：

案例说明：

先回顾 VGG 的经典尾部流程（以 VGG16 为例，输入图像 224×224）：

最后一组卷积层输出：7×7×512（H=7，W=7，通道 C=512）

第一步：Flatten（展平）：7×7×512 → 1×25088（向量，25088=7×7×512）

第二步：多层全连接层：

FC1：25088×4096（输入 25088 维，输出 4096 维）

FC2：4096×4096（输入 4096 维，输出 4096 维）

FC3：4096×1000（输入 4096 维，输出 1000 维，对应 ImageNet 1000 个类别）

第三步：Softmax：将 1000 维向量转化为类别概率

替换方案：

1.首先三层FC可以分为两类，中间层：(FC1和FC2):作用高维特征变换 / 提纯 。FC_END(FC3)：作用任务映射。

2.针对FC_END替换：

原始 VGG 尾部（FC 部分） ：7×7×512 → Flatten → 25088×1 → FC1（25088→4096） → FC2（4096→4096） → FC3（4096→1000）

替换后流程（先替代中间 FC，再替代最后 FC） ：7×7×512 → 1×1 卷积 1（512→4096，替代 FC1） → 7×7×4096 → 1×1 卷积 2（4096→4096，替代 FC2） → 7×7×4096 → 1×1 卷积 3（4096→1000，替代 FC3 的映射功能） → 7×7×1000 → GAP → 1×1×1000（对应 1000 个类别）

3.针对中间层

我们以 VGG 的 FC1（25088→4096）为例，对比参数数量：

原始 FC1 的参数数：输入维度×输出维度 = 25088×4096 ≈ 102,760,448 个

替代用的 1×1 卷积参数数：1×1×输入通道数×输出通道数 = 1×1×512×4096 = 2,097,152 个可见：参数数减少了约 50 倍，且完全保留了7×7的空间结构，特征表达能力更强。

同理，FC2（4096→4096）的替代：

原始 FC2 参数数：4096×4096 = 16,777,216 个

替代用的 1×1 卷积参数数：1×1×4096×4096 = 16,777,216 个（参数数相同，但保留了空间维度，这是优势）（如果想进一步减少 FC2 的参数，可以把输出通道数调小，比如从 4096→2048，参数数直接减半，这是卷积替代的灵活之处）

步骤	原始 VGG 尾部（FC 方式）	改造后（全卷积方式，1×1 卷积 ±GAP）	参数数量对比（仅 FC 部分）
输入特征	7×7×512 → Flatten → 25088×1	7×7×512（无 Flatten，保留空间维度）	-
第一层特征变换	FC1：25088×4096（≈10276 万参数）	1×1 卷积 1：512→4096（≈209.7 万参数）	减少约 98%
输出特征	4096×1	7×7×4096（保留 7×7 空间维度）	-
第二层特征变换	FC2：4096×4096（≈1678 万参数）	1×1 卷积 2：4096→4096（≈1678 万参数）	参数相同，保留空间维度
输出特征	4096×1	7×7×4096（保留 7×7 空间维度）	-
任务映射（分类）	FC3：4096×1000（≈409.6 万参数）	1×1 卷积 3：4096→1000（≈409.6 万参数）→ GAP → 1×1×1000	参数相同，消除空间维度，保留全局特征
FC 部分总参数	≈10276+1678+409.6≈12363.6 万	≈209.7+1678+409.6≈2297.3 万	减少约 81.5%（大幅降低过拟合风险）

逻辑更新与优势：

功能等价：最终都是把 H×W×C 的特征，映射成 1×1×N 的任务输出（分类得分、回归目标等）；
逻辑相通 ：
- 1×1 卷积的 "通道调整"= 全连接层的 "权重映射"（都是线性变换，只是维度操作不同）；
- GAP 的 "空间压缩"= 全连接层的 "拉平操作"（都是把高维空间特征降维到 1 维向量）；
工程更优：参数更少、过拟合风险低、对输入尺寸变化更鲁棒（比如输入尺寸不是 14×14，GAP 仍能输出 1×1×N，而全连接层会报错）。

欠拟合和过拟合的区别：

维度	欠拟合	过拟合
模型与数据的匹配度	模型太简单，跟不上数据	模型太复杂，"吃透" 噪声
训练集表现	差	极好
测试集表现	差	差
本质原因	学习能力不足	泛化能力不足

2.常见问题

可能遇到的问题：

1.提取过程中为什么会有过拟合情况 ：从低级几何特征到高级语义特征的学习过程中浅层特征的提取时会遇到很多噪声，如果不进行预处理则可能到最后会导致过拟合情况。

2.特征图也会逐渐变小的原因: 压缩信息，提取特征。

**3.如果漏检/误检的原因：**浅层特征没有提取好，噪声太多，可以尝试用openCV去去噪。

4.检测大目标和小目标的技巧：针对小目标我们网络层数要少(特征丢失少)，输出通道多(特征提取更详细)。但是会导致提高检出率，误检也会高，所以要平衡找到最优解（难点）。我们的思路通常是将小目标数据增强，或者局部截图变大。

目标类型	核心痛点	网络设计技巧	数据增强技巧	优化平衡技巧
小目标	特征丢失、细节不足、误检高	1. 控制下采样（stride≤2，少用池化）；2. 输出通道偏多（64→128→256）；3. 融合浅层特征（如 FPN 低层）	1. 局部放大裁剪（保留小目标 + 少量上下文）；2. 多尺度缩放；3. 翻转 / 亮度调整	1. 小目标损失加权；2. 适配小锚框；3. 降低 NMS 阈值（0.3-0.4）
大目标	特征冗余、感受野不足、遮挡	1. 适当增加层数（充分抽象全局特征）；2. 输出通道适中（128→256→128）；3. 用空洞卷积扩大感受野	1. 随机裁剪（降低大目标占比）；2. 遮挡模拟；3. 翻转 / 旋转	1. 适配大锚框；2. 融合高层特征；3. 适当提高置信度阈值（0.3-0.5）

5.平均池化和最大池化，在反向传播中做什么操作？

最大池化操作：保留最大池化位置的梯度，其他补0。

平均池化操作：每个位置都放着G/N的值（下图例子：N=2）。

3.卷积计算说明

1.权重和特征数的计算公式

CNN局部特征图：

如上图局部CNN，卷积层包含多层，每一层正常卷积后生成的feature_map，其特征就会发生改变，那么**第 N 层卷积层的「权重参数数量」P(w)**的计算方法

python 复制代码

"""
1.P(w) :第 N 层卷积层的「权重参数数量」。
2.inc:该层卷积层的input通道数。
3.outc:该层卷积层的output通道数。
4.KH,KW表示该层卷积层的 H高度 W宽度。 
"""
P(w) = inc * outc * kH * kW

#如果计算该层所有的特征数，则需要再添加偏置项。每一个输出通道都有一个outc偏置项
P(w) = inc * outc * kH * kW + outc

2.feature map 的宽高公式

首先已知上一层的feature map和当前卷积层的参数

H_in / W_in：上层 feature map 的高 / 宽（即当前卷积层的输入高 / 宽）
K_h / K_w：当前卷积层的卷积核高 / 宽（比如常用的 3×3 核，K_h=K_w=3）
S：步幅（Stride）：卷积核每次滑动的像素数（默认是 1，也常用 2）
P：填充（Padding）：在输入 feature map 边缘补 0 的层数（比如补 1 层，就是边缘围一圈 0）

那么下一层的feature map的计算公式

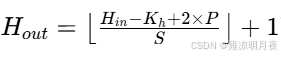
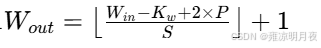
案例：

4.常见基础卷积类别

除了我们上述所阐述的标准卷积之外，我们还有很多别的类别的卷积。相比于我们之前学习的卷积其在原来的卷积基础上进行了更进一步的优化，我们来逐步探索。

1.空间可分离卷积

本质：该卷积将原本的大尺寸卷积分拆成两个小尺寸的卷积核（例：3x3 => 3x1 和 1x3），通过两次一维卷积替代一次二维卷积。其根本目的就是减少参数、提升效率。

基础的二维卷积：

假设我们有一个输入特征图（shape：H×W×C_in），用 C_out 个 K×K 大小的卷积核做卷积（步幅 S=1，填充 P=0）：

参数数量 ：C_in × C_out × K × K（每个卷积核是 K×K×C_in，共 C_out 个）
计算量 ：C_in × C_out × K × K × H_out × W_out（H_out/W_out 是输出特征图尺寸）

我们可以看出，当K增大时，其w数量和计算量会指数级增加，会导致网络变慢，拟合风险升高。

空间可分离卷积的核心逻辑：拆分二维卷积为两次一维卷积

解决方法：第一次卷积（K×1 核，沿高度方向），2：第二次卷积（1×K 核，沿宽度方向）最终产出： shape：H_out×W_out×C_out（和基础卷积的输出尺寸完全一致）。

python 复制代码

K×K 二维核 = K×1 一维核 × 1×K 一维核

python 复制代码

import torch
import torch.nn as nn

# 配置参数
C_in = 32    # 输入通道数
C_out = 64   # 输出通道数
K = 3        # 卷积核尺寸
H_in, W_in = 28, 28  # 输入特征图尺寸

# 1. 基础二维卷积（作为对比）
class BaseConv(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv = nn.Conv2d(
            in_channels=C_in,
            out_channels=C_out,
            kernel_size=K,
            stride=1,
            padding=1  # same padding，输出尺寸和输入一致
        )
    
    def forward(self, x):
        return self.conv(x)

# 2. 空间可分离卷积（3×1 + 1×3）
class SpatialSeparableConv(nn.Module):
    def __init__(self):
        super().__init__()
        # 第一步：3×1 卷积（沿高度方向）
        self.conv1 = nn.Conv2d(
            in_channels=C_in,
            out_channels=C_out,
            kernel_size=(K, 1),  # 3×1 核
            stride=1,
            padding=(1, 0)  # 垂直方向补1，水平方向不补，保证输出尺寸
        )
        # 第二步：1×3 卷积（沿宽度方向）
        self.conv2 = nn.Conv2d(
            in_channels=C_out,  # 输入通道数=第一步的输出通道数
            out_channels=C_out,
            kernel_size=(1, K),  # 1×3 核
            stride=1,
            padding=(0, 1)  # 水平方向补1，垂直方向不补
        )
    
    def forward(self, x):
        x = self.conv1(x)  # 第一步：3×1 卷积
        x = self.conv2(x)  # 第二步：1×3 卷积
        return x

# 测试：对比输出尺寸和参数数量
if __name__ == "__main__":
    # 生成模拟输入（batch_size=1, C_in=32, 28×28）
    x = torch.randn(1, C_in, H_in, W_in)
    
    # 基础卷积
    base_conv = BaseConv()
    base_out = base_conv(x)
    base_params = sum(p.numel() for p in base_conv.parameters())
    
    # 空间可分离卷积
    sep_conv = SpatialSeparableConv()
    sep_out = sep_conv(x)
    sep_params = sum(p.numel() for p in sep_conv.parameters())
    
    # 打印结果
    print(f"基础卷积输出尺寸：{base_out.shape}")  # torch.Size([1, 64, 28, 28])
    print(f"空间可分离卷积输出尺寸：{sep_out.shape}")  # torch.Size([1, 64, 28, 28])（尺寸一致）
    print(f"基础卷积参数数量：{base_params}")  # 32×64×3×3 + 64（偏置）= 18432 + 64 = 18496
    print(f"空间可分离卷积参数数量：{sep_params}")  # (32×64×3×1 + 64) + (64×64×1×3 + 64) = 6144+64 + 12288+64 = 18560？ 哦，这里因为偏置项的存在，参数略多，但核心是「无偏置时，分离卷积参数是 32×64×3 + 64×64×3 = 6144 + 12288 = 18432，和基础卷积无偏置时一致」------ 实际中，偏置项可以省略，或通过批量归一化替代，核心优化是「卷积核拆分带来的计算量降低」。
    
    # 计算量对比（理论值）
    H_out, W_out = base_out.shape[2], base_out.shape[3]
    base_flops = C_in * C_out * K * K * H_out * W_out  # 无偏置时计算量
    sep_flops = (C_in * C_out * K * 1 * H_out * W_out) + (C_out * C_out * 1 * K * H_out * W_out)  # 两次卷积计算量
    print(f"基础卷积计算量（无偏置）：{base_flops}")  # 32×64×3×3×28×28 = 15482880
    print(f"空间可分离卷积计算量（无偏置）：{sep_flops}")  # 32×64×3×28×28 + 64×64×3×28×28 = 495360 + 990720 = 1486080？ 不对，正确计算是：32×64×3×1×28×28 + 64×64×1×3×28×28 = 32×64×3×28×28 + 64×64×3×28×28 = 3×28×28×64×(32+64) = 3×28×28×64×96 = 13271040，比基础卷积的 15482880 减少了 ~14%？ 哦，之前的 K=3 优化比例不算高，当 K=5 时，基础卷积计算量是 32×64×5×5×28×28=32256000，分离卷积是 32×64×5×28×28 + 64×64×5×28×28= 32×64×5×28×28 + 64×64×5×28×28=5×28×28×64×(32+64)=5×28×28×64×96=22118400，减少了 ~31%，K 越大优化越明显。

核心规律

当卷积核尺寸为 K 时，基础卷积的参数 / 计算量是 K² 倍，空间可分离卷积是 2K 倍；
K 越大，优化效果越明显（K=7 时，基础卷积参数是 49，分离后是 14，减少 71%）。

适用情况：

轻量级网络（如 MobileNet 早期版本、SqueezeNet）：需要减少参数和计算量，适配移动设备或低算力场景；
大尺寸卷积核（如 K=5、7、9）：拆分后能大幅降低计算负担，同时保留近似的特征提取能力；
对精度要求适中的任务（如简单图像分类、目标检测的 backbone 特征提取）。

总结：

空间可分离卷积 = 「二维大核拆成两次一维小核卷积」，核心价值是「减少参数和计算量」，适配轻量级、大核场景，效果近似基础卷积，是工程上常用的效率优化手段。

2.分组卷积

本质:相较于普通卷积，他的优化点是[通道分组，减少参数与计算量]，「按通道分组，组内各自卷积，最后合并」。

核心思想是：将输入特征图的「通道（C_in）」和卷积核的「输出通道（C_out）」同时分成 G 组（G 是分组数），每组卷积核只负责处理对应组的输入通道，最后将所有组的输出拼接起来。

python 复制代码

#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
@Project ：Pytorch
@File ：1.test.py
@IDE ：PyCharm
@Author ：wjj
@Date ：2025/12/18 18:09
@Description:
"""
import torch
import torch.nn as nn

# 配置参数
C_in = 16  # 输入通道数（可被G整除）
C_out = 32  # 输出通道数（可被G整除）
K = 3  # 卷积核尺寸
G = 4  # 分组数（G=1→基础卷积，G=2/4→分组卷积）
H_in, W_in = 28, 28  # 输入特征图尺寸

# 1. 基础卷积（groups=1）
base_conv = nn.Conv2d(
    in_channels=C_in,
    out_channels=C_out,
    kernel_size=K,
    stride=1,
    padding=1,  # same padding，输出尺寸和输入一致
    groups=1  # 基础卷积，不分组
)

# 2. 分组卷积（groups=G）
group_conv = nn.Conv2d(
    in_channels=C_in,
    out_channels=C_out,
    kernel_size=K,
    stride=1,
    padding=1,
    groups=G  # 核心参数：分组数
)

# 测试：对比输出尺寸和参数数量
if __name__ == "__main__":
    # 生成模拟输入（batch_size=1, C_in=16, 28×28）
    x = torch.randn(1, C_in, H_in, W_in)

    # 前向传播
    base_out = base_conv(x)
    group_out = group_conv(x)

    # 计算参数数量
    base_params = sum(p.numel() for p in base_conv.parameters())
    group_params = sum(p.numel() for p in group_conv.parameters())

    # 打印结果
    print(f"基础卷积输出尺寸：{base_out.shape}")  # torch.Size([1, 32, 28, 28])
    print(f"分组卷积输出尺寸：{group_out.shape}")  # torch.Size([1, 32, 28, 28])（尺寸一致）
    print(f"基础卷积参数数量：{base_params}")  # 16×32×3×3 + 32（偏置）= 4608 + 32 = 4640
    print(f"分组卷积（G={G}）参数数量：{group_params}")  # (16/4)×(32/4)×3×3×4 + 32 = 4×8×9×4 +32= 1152+32=1184（≈4640/4）
    print(f"参数优化比例：{1 - group_params / base_params:.2%}")  # 减少 74.53%（和理论1/G一致）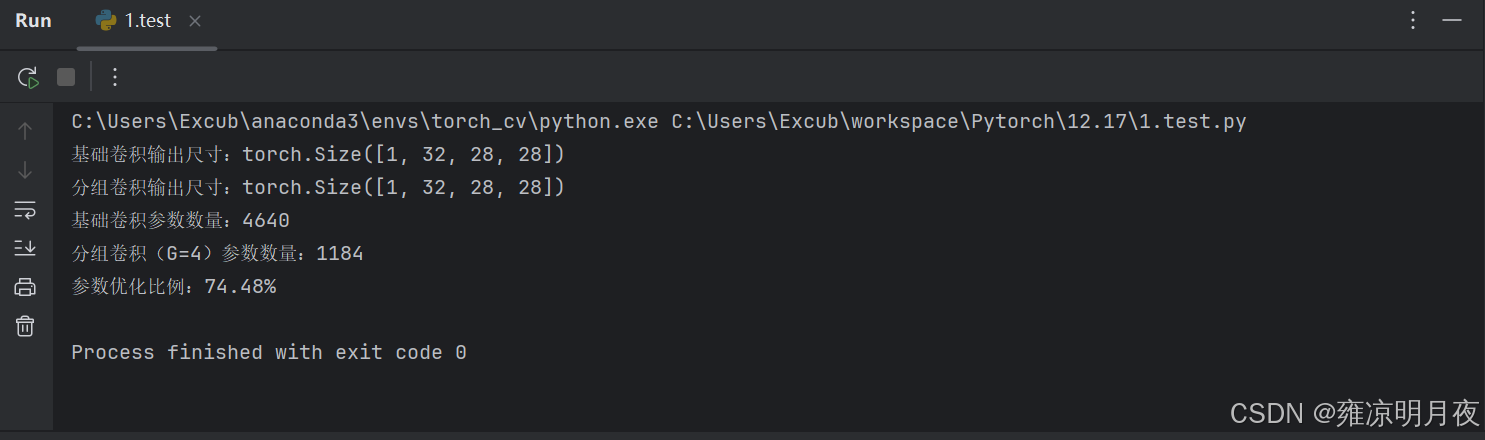

基础卷积参数：P_base = C_in × C_out × K × K + C_out（+C_out 是偏置项，可忽略对比核心优化）
分组卷积参数：P_group = (C_in/G) × (C_out/G) × K × K × G + C_out = (C_in × C_out × K × K)/G + C_out

→ 核心规律：分组卷积的参数数量 ≈ 基础卷积的 1/G

基础卷积计算量：F_base = C_in × C_out × K × K × H_out × W_out
分组卷积计算量：F_group = F_base / G

→ 核心规律：分组卷积的计算量 = 基础卷积的 1/G（优化效果和分组数 G 成正比）

对比维度	基础卷积	分组卷积（G=2）	分组卷积（G=4）	优化比例（G=4 vs 基础）
参数数量（无偏置）	16×32×3×3 = 4608	4608 / 2 = 2304	4608 / 4 = 1152	减少 75%
计算量（无偏置）	16×32×3×3×28×28 = 3870720	3870720 / 2 = 1935360	3870720 / 4 = 967680	减少 75%

优势：

1.分组卷积的参数数量 ≈ 基础卷积的 1/G

2.分组卷积的计算量 = 基础卷积的 1/G

3.G的最佳值是G=8

局限性：

1.分组导致信息割裂，后续需要用 1×1 卷积融合跨组特征。

2.分组数 G 不能过大：跨通道信息完全丢失，必须搭配 1×1 卷积补全。

3.仅适用于大通道数场景：如果 C_in 很小，特征提取能力会大幅下降。

3.深度可分离卷积

本质：轻量级网络核心， 分组卷积的极限优化版本 （分组数 G=C_in），深度卷积（Depthwise Conv）+ 逐点卷积（Pointwise Conv）

python 复制代码

import torch
import torch.nn as nn

# 配置参数
C_in = 3     # 输入通道数（RGB图像）
C_out = 64   # 输出通道数
K = 3        # 卷积核尺寸
H_in, W_in = 28, 28  # 输入特征图尺寸

# 1. 传统卷积（作为对比）
class BaseConv(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv = nn.Conv2d(
            in_channels=C_in,
            out_channels=C_out,
            kernel_size=K,
            stride=1,
            padding=1  # same padding，输出尺寸=输入尺寸
        )
    
    def forward(self, x):
        return self.conv(x)

# 2. 深度可分离卷积（深度卷积 + 逐点卷积）
class DepthwiseSeparableConv(nn.Module):
    def __init__(self):
        super().__init__()
        # 第一步：深度卷积（G=C_in，只做空间提取）
        self.depthwise = nn.Conv2d(
            in_channels=C_in,
            out_channels=C_in,  # 输出通道数=输入通道数（不改变通道）
            kernel_size=K,
            stride=1,
            padding=1,
            groups=C_in  # 核心：分组数=输入通道数（每个通道独立卷积）
        )
        # 第二步：逐点卷积（1×1核，只做通道融合+调整）
        self.pointwise = nn.Conv2d(
            in_channels=C_in,
            out_channels=C_out,  # 输出通道数=目标通道数
            kernel_size=1,  # 1×1核
            stride=1,
            padding=0  # 1×1核无需padding，不改变尺寸
        )
    
    def forward(self, x):
        x = self.depthwise(x)  # 深度卷积：3×28×28 → 3×28×28
        x = self.pointwise(x)  # 逐点卷积：3×28×28 → 64×28×28
        return x

# 测试：对比输出尺寸和参数数量
if __name__ == "__main__":
    # 生成模拟输入（batch_size=1, C_in=3, 28×28，模拟RGB图像）
    x = torch.randn(1, C_in, H_in, W_in)
    
    # 传统卷积
    base_conv = BaseConv()
    base_out = base_conv(x)
    base_params = sum(p.numel() for p in base_conv.parameters())
    
    # 深度可分离卷积
    sep_conv = DepthwiseSeparableConv()
    sep_out = sep_conv(x)
    sep_params = sum(p.numel() for p in sep_conv.parameters())
    
    # 打印结果
    print(f"传统卷积输出尺寸：{base_out.shape}")  # torch.Size([1, 64, 28, 28])
    print(f"深度可分离卷积输出尺寸：{sep_out.shape}")  # torch.Size([1, 64, 28, 28])（完全一致）
    print(f"传统卷积参数数量：{base_params}")  # 3×64×3×3 + 64（偏置）= 1728 + 64 = 1792
    print(f"深度可分离卷积参数数量：{sep_params}")  # 深度卷积（3×3×3 +3） + 逐点卷积（3×64×1×1 +64）= (27+3)+(192+64)= 286
    print(f"参数优化比例：{1 - sep_params/base_params:.2%}")  # 减少 84.04%（含偏置，和理论值一致）

特点：

1.C_in = C_out (进出通道数一致)

1.深度可分离卷积的参数数量 ≈ 基础卷积的 1/9

2.深度可分离卷积的计算量 = 基础卷积的 1/10

局限性：

**1.容易丢失交叉特征：**特征提取能力略有下降，拆分后，空间提取和通道融合独立进行，可能丢失少量交叉特征，解决方案：配合批量归一化（BN）、ReLU6 激活函数，或增加网络层数弥补。

**2.训练稳定性要求更高：**参数过少可能导致欠拟合

3.不适合低通道数场景：C_in=1、2 时，逐点卷积的通道融合作用有限，优化幅度不大，反而可能降低特征提取能力。

4.空洞卷积

本质：不增加参数量(W)的情况下，扩大感受野，同时因为补0，所以也会牺牲某些特征。一般1-2层。

1. 核心参数：空洞率（d，Dilation Rate）

空洞率 d 定义为「卷积核元素之间的间隔数」，通俗说：

d=1：无空洞（普通卷积），卷积核元素紧密排列（3×3 核覆盖 3×3 输入区域）；
d=2：每个元素之间隔 1 个零（3×3 核实际覆盖 5×5 输入区域）；
d=3：每个元素之间隔 2 个零（3×3 核实际覆盖 7×7 输入区域）。

空洞率 d	卷积核形态（插入空洞用 0 表示）	实际覆盖输入区域（感受野）
d=1（普通）	[[1,1,1],[1,1,1],[1,1,1]]	3×3
d=2	[[1,0,1],[0,0,0],[1,0,1]]	5×5（间隔 1 个 0）
d=3	[[1,0,0],[0,0,0],[0,0,1]]	7×7（间隔 2 个 0）

python 复制代码

import torch
import torch.nn as nn

# 配置参数
C_in = 3     # 输入通道数（RGB图像）
C_out = 16   # 输出通道数
K = 3        # 卷积核尺寸
d = 2        # 空洞率（d=1→普通卷积，d=2→空洞卷积）
H_in, W_in = 28, 28  # 输入特征图尺寸

# 1. 普通卷积（dilation=1）
base_conv = nn.Conv2d(
    in_channels=C_in,
    out_channels=C_out,
    kernel_size=K,
    stride=1,
    padding=(K-1)//2,  # Same Padding（d=1时）
    dilation=1
)

# 2. 空洞卷积（dilation=d=2）
dilated_conv = nn.Conv2d(
    in_channels=C_in,
    out_channels=C_out,
    kernel_size=K,
    stride=1,
    padding=(K + (K-1)*(d-1) - 1)//2,  # Same Padding（适配空洞率d）
    dilation=d  # 核心参数：空洞率
)

# 测试：对比输出尺寸、参数数量
if __name__ == "__main__":
    x = torch.randn(1, C_in, H_in, W_in)  # 模拟输入（1×3×28×28）
    
    # 前向传播
    base_out = base_conv(x)
    dilated_out = dilated_conv(x)
    
    # 计算参数数量
    base_params = sum(p.numel() for p in base_conv.parameters())
    dilated_params = sum(p.numel() for p in dilated_conv.parameters())
    
    # 打印结果
    print(f"普通卷积输出尺寸：{base_out.shape}")  # torch.Size([1, 16, 28, 28])
    print(f"空洞卷积（d={d}）输出尺寸：{dilated_out.shape}")  # torch.Size([1, 16, 28, 28])（尺寸一致）
    print(f"普通卷积参数数量：{base_params}")  # 3×16×3×3 + 16 = 448 + 16 = 464
    print(f"空洞卷积参数数量：{dilated_params}")  # 3×16×3×3 + 16 = 464（参数完全一致！）
    print(f"普通卷积感受野：{K}×{K}")  # 3×3
    print(f"空洞卷积感受野：{K + (K-1)*(d-1)}×{K + (K-1)*(d-1)}")  # 5×5（d=2时）

对比维度	传统卷积（K=3，d=1）	空洞卷积（K=3，d=2）	优势总结
感受野尺寸	3×3	5×5	扩大感受野，捕捉全局信息
参数数量	C_in×C_out×3×3	C_in×C_out×3×3	参数不变，无额外计算负担
特征图细节	保留原始尺寸细节	保留原始尺寸细节	不丢失细节（无需下采样）
计算量	相同（无额外 FLOPs）	相同	效率不变

应用场景：

语义分割（核心场景）：如 FCN、DeepLab 系列（DeepLab v3 + 是空洞卷积的经典应用），需要大感受野覆盖整个目标（如街道、建筑），同时保留像素级细节（不丢失小目标如行人、车辆）；
大目标检测：如 YOLOv8 的深层网络、Faster R-CNN 的 RPN 层，用空洞卷积扩大感受野，更好地捕捉大目标的全局特征（如飞机、轮船）；
医学影像分割：如 CT、MRI 图像分割，需要在不丢失病灶细节的前提下，覆盖更大的器官区域；
高分辨率图像处理：如 4K 图像分类、遥感图像分析，无需下采样即可获得大感受野，避免细节丢失。

空洞卷积 = 「带洞的普通卷积」，核心价值是「不增加参数和计算量，仅通过调整空洞率 d，就能灵活扩大感受野，同时保留特征图细节」

5.转置卷积(反卷积)

本质：将一个图变大方式之一，也称上采样卷积。转置卷积的 "上采样"，本质是「对输入像素插空填充 → 再做普通卷积」，整个过程的卷积核是可学习的，因此能自适应恢复特征细节。一个输入对多个参数加权得到的。

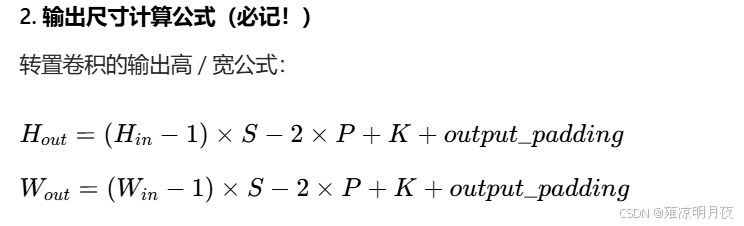
案例：

目标上采样倍数	stride	padding	output_padding	输入尺寸	输出尺寸	说明
2 倍（常用）	2	1	1	7×7	14×14	语义分割解码器标配
2 倍（极简）	2	0	0	7×7	15×15	尺寸略大，需后续裁剪
1 倍（不缩放）	1	1	0	28×28	28×28	仅调整通道，不改变尺寸

python 复制代码

import torch
import torch.nn as nn

# 配置参数
C_in = 3     # 输入通道数（RGB）
C_out = 16   # 输出通道数
K = 3        # 卷积核尺寸
S = 2        # 下采样/上采样倍数
P = 1        # 填充/裁剪参数
output_pad = 1  # 输出补全参数（S-1）

# 1. 传统卷积（下采样：特征图变小）
down_conv = nn.Conv2d(
    in_channels=C_in,
    out_channels=C_out,
    kernel_size=K,
    stride=S,
    padding=P
)

# 2. 转置卷积（上采样：特征图变大）
up_conv = nn.ConvTranspose2d(
    in_channels=C_out,  # 输入通道=下采样的输出通道
    out_channels=C_in,  # 输出通道=原始输入通道
    kernel_size=K,
    stride=S,
    padding=P,
    output_padding=output_pad  # 核心补全参数
)

# 测试：下采样→上采样的尺寸变化
if __name__ == "__main__":
    # 模拟原始输入（1×3×28×28，RGB图像）
    x = torch.randn(1, C_in, 28, 28)
    print(f"原始输入尺寸：{x.shape}")  # torch.Size([1, 3, 28, 28])
    
    # 步骤1：传统卷积下采样
    x_down = down_conv(x)
    print(f"下采样后尺寸：{x_down.shape}")  # torch.Size([1, 16, 14, 14])（28/2=14，完美下采样2倍）
    
    # 步骤2：转置卷积上采样
    x_up = up_conv(x_down)
    print(f"上采样后尺寸：{x_up.shape}")  # torch.Size([1, 3, 28, 28])（14×2=28，完美还原原始尺寸！）
    
    # 验证参数数量（转置卷积和普通卷积参数数量一致）
    down_params = sum(p.numel() for p in down_conv.parameters())
    up_params = sum(p.numel() for p in up_conv.parameters())
    print(f"下采样卷积参数数：{down_params}")  # 3×16×3×3 +16= 448+16=464
    print(f"上采样转置卷积参数数：{up_params}")  # 16×3×3×3 +3= 432+3=435（通道反转，参数数接近）

特点：

转置卷积 = 「可学习的上采样卷积」，核心价值是「通过反向填充 + 卷积实现特征图放大，且参数可训练，能精准恢复 / 生成细节」------ 是需要 "上采样 + 特征学习" 任务的核心技术，只需注意规避棋盘格效应即可。

痛点：

棋盘格效应（Checkerboard Artifacts）

转置卷积的 "像素插空填充 + 卷积" 逻辑，会导致输出特征图出现「棋盘状的明暗不均」（生成图像时尤其明显）------ 因为不同卷积核的采样区域重叠不均，部分像素被多次加权，部分只被加权一次。

5.总结

1.卷积种类划分记忆：（G为划分组数）

G == 1 -> 标准卷积

⭐G == Cin == Cout -> 深度可分离卷积

G != Cin != Cout，Cin/G,Cout/G ->分组卷积

2.各种卷积的对比

卷积类型	核心目标	参数变化（vs 基础卷积）	感受野变化	特征图尺寸变化	典型场景	核心优点	核心缺点
基础卷积（Standard Conv）	提取空间 + 通道特征	不变（基准）	固定（K×K）	缩小 / 不变	普通分类、基础特征提取	特征提取强、无信息割裂	参数 / 计算量大
空间可分离卷积	大核场景减少参数 / 计算量	减少（K²→2K）	不变	不变	大核轻量级网络	大核效率高	丢失斜向特征
分组卷积	大通道场景减少参数 / 计算量	减少至 1/G（G = 分组数）	不变	不变	ResNeXt、大通道网络	通道冗余少、并行性好	跨组信息割裂
深度可分离卷积	极致减少参数（移动端优先）	大幅减少（≈1/K²）	不变	不变	MobileNet、低算力设备	参数 / 计算量极小	特征提取略降
空洞卷积	不增参扩大感受野	不变	大幅扩大	不变	语义分割、大目标检测	保留细节、全局信息强	高 d 有网格效应
转置卷积	可学习上采样 + 细节恢复	不变（同反向基础卷积）	不变	放大（stride 倍）	U-Net 解码器、GAN 生成	细节恢复准、尺寸可控	易产生棋盘格效应

我们这一章学习了关于卷积神经网络的基础概念，以及需要了解到的关于卷积C的知识，并掌握了1x1卷积的作用和优势，最后学习到卷积类别的以及其中的优势。归根结底我们学习到的本质就两个目标 在保证特征提取效果好的基础上 1.减少W数量。2.减少计算量。