【VLMs篇】11：用于端到端目标检测的可变形Transformers(Deformable DETR)

1. 论文摘要介绍表

维度	内容总结
痛点问题	1. 收敛慢：DETR 需要 500 个 epoch 才能收敛，比 Faster R-CNN 慢 10-20 倍。 2. 小目标差：DETR 难以处理高分辨率特征图（复杂度 O(N2)O(N^2)O(N2)），导致小物体检测性能低。
核心创新	1. 可变形注意力 (Deformable Attention) ：不再关注所有像素，只对参考点周围的一小部分关键点进行稀疏采样。 2. 多尺度注意力 (Multi-scale Attention) ：无需 FPN，在注意力模块内部直接融合多尺度特征。 3. 迭代边界框细化：解码器层层递进优化预测框。
主要成果	1. 训练加速：仅需 50 个 epoch 即可达到甚至超过 DETR 500 个 epoch 的性能（10倍加速）。 2. 性能提升：在小物体检测上提升显著（APS_SS 提升 2.9%）。 3. 复杂度降低：计算复杂度从随空间大小二次方增长降低为线性增长。
关键技术	稀疏采样、参考点 (Reference Points)、双线性插值、多尺度特征融合。

2. 论文具体实现流程

A. 输入 (Input):

原始图像 III。

B. 数据流转与逻辑 (Pipeline):

特征提取 (Backbone):
- 图像经过 ResNet-50 提取特征。
- 多尺度构建 : 提取 C3, C4, C5 层特征，并通过卷积生成 C6 层，构建 4 层多尺度特征图 {xl}\{x^l\}{xl}。
编码器 (Deformable Encoder):
- 输入：多尺度特征图 + 位置编码 + 尺度层级编码 (Scale-level embedding)。
- 逻辑：每个像素作为 Query，参考点为自身位置。
- 操作：应用 多尺度可变形自注意力 (MSDeformAttn)，在不同尺度层级上采样关键点并聚合特征。
- 输出：增强后的多尺度特征图。
解码器 (Deformable Decoder):
- 输入：对象查询 (Object Queries) + 编码器输出的特征图。
- 逻辑：
  - 交叉注意力 (Cross-Attention) ：被替换为 多尺度可变形注意力 。Query 是对象查询，Key 是编码器特征。参考点 p^q\hat{p}_qp^q 由对象查询通过线性层预测。
  - 自注意力 (Self-Attention)：保持标准 Transformer 自注意力，处理对象查询之间的关系。
- 迭代细化：每一层解码器都预测相对于参考点的边界框偏移，并更新下一层的参考点。
预测头 (Detection Head):
- 分类分支：预测物体类别。
- 回归分支：预测边界框的相对偏移（相对于参考点）。

C. 输出 (Output):

NNN 个预测结果，每个包含：类别置信度 + 归一化边界框 (x,y,w,h)(x, y, w, h)(x,y,w,h)。

3. 有趣的白话版详细解说

Deformable DETR：近视眼变身火眼金睛神探

背景：

以前有个叫 DETR 的神探（目标检测模型），他很厉害，不需要像老前辈（Faster R-CNN）那样还要先画一堆框框（Anchor）再去挑。DETR 也就是"看一眼"就能告诉你图里有啥。
但是，DETR 有两个大毛病：

反应慢（收敛慢）： 训练他太费劲了，得教他看图看几百遍（500 epochs）他才能学会，这比教老前辈慢了十几倍。
眼神不好（小物体看不清）： 如果图里有很小的东西（比如远处的一只鸟），他往往看不见。因为他为了省脑子，不敢看太高清晰度的大图，不然脑子（显存/计算量）会炸掉。

为什么 DETR 这么"轴"？

因为 DETR 用的是标准的"注意力机制"。这就像让他找图里的猫，他会死板地盯着图里的每一个像素点看，不管这个点是在猫身上还是在无聊的天空上。这种"地毯式搜索"极其浪费时间，而且图越大，计算量是爆炸式增长的（平方级复杂度）。

Deformable DETR 怎么解决的？

作者给 DETR 配了一副"智能眼镜"，把他升级成了 Deformable DETR 。

这个新眼镜有两个黑科技：

只看重点（稀疏采样）：

现在，通过"可变形注意力"，神探不再傻乎乎看全图了。对于每一个查询点，他只看周围几个关键点。这就好比找猫时，直接盯着"耳朵尖"、"尾巴"、"眼睛"这几个关键位置看，忽略背景。无论图多大，他看的点数是固定的，所以速度飞快，脑子也不炸了。
变焦观察（多尺度融合）：

以前 DETR 只能在一个固定的放大倍数下看图。现在他能同时看"远景"、"中景"、"近景"（多尺度特征）。找大象就看远景，找蚂蚁就看近景。这让他在抓小物体时特别准。

主要流程是啥样？

照片进来，先通过普通眼镜（ResNet）提取出不同大小的特征图（多尺度）。
编码器（大脑整理）：用新学会的"只看重点"技能，在这些特征图上扫视，把有用的信息聚合起来。
解码器（最终判断）：这时候派出一堆"探员"（Object Queries）。每个探员先猜一个位置（参考点），然后用"新眼镜"去那个位置周围瞄一眼，看看有没有物体。如果有，就根据看到的微调一下框的位置。
反复确认（迭代细化）：这个过程会重复几次（层），像福尔摩斯一样："初步判断在左边 -> 放大看 -> 修正位置 -> 确定是只猫"。

结果怎么样？

学得快： 以前教 500 遍，现在教 50 遍就出师了，而且成绩更好。
眼神好： 小东西看得清清楚楚。

个人观点：

这篇论文非常重要，属于填坑之作。DETR 刚出来时虽然惊艳，但那个训练时长和计算开销劝退了很多人。Deformable DETR 借用了 CV 领域经典的"可变形卷积（DCN）"思想，成功解决了 Transformer 在视觉任务上"太关注全局从而忽略局部效率"的痛点。它让端到端的 Transformer 检测器真正变得"好用"且"可落地"了，是后续一系列改进模型（如 DINO 等）的鼻祖级基石。它告诉我们：在计算机视觉里，完全的全局注意力太奢侈了，带有先验知识的"稀疏关注"才是王道。

4. 论文完整翻译

摘要 (ABSTRACT)

DETR 最近被提出用于消除目标检测中许多手工设计的组件，并展示了良好的性能。然而，由于 Transformer 注意力模块在处理图像特征图时的局限性，它存在收敛速度慢和特征空间分辨率有限的问题。为了缓解这些问题，我们提出了 Deformable DETR，其注意力模块仅关注参考点周围的一小组关键采样点。Deformable DETR 可以通过减少 10 倍的训练轮次（epochs）实现比 DETR 更好的性能（特别是在小物体上）。在 COCO 基准测试上的大量实验证明了我们方法的有效性。代码发布于：https://github.com/fundamentalvision/Deformable-DETR。

1 引言 (INTRODUCTION)

现代目标检测器采用许多手工设计的组件（Liu et al., 2020），例如锚框生成（anchor generation）、基于规则的训练目标分配、非极大值抑制（NMS）后处理。它们并非完全端到端的。最近，Carion 等人（2020）提出了 DETR 来消除对这些手工设计组件的需求，并构建了第一个完全端到端的目标检测器，取得了非常有竞争力的性能。DETR 利用了一种简单的架构，结合了卷积神经网络（CNN）和 Transformer（Vaswani et al., 2017）编码器-解码器。它们利用 Transformer 通用且强大的关系建模能力来替代手工设计的规则，并在适当设计的训练信号下进行工作。

尽管设计有趣且性能良好，但 DETR 也有其自身的问题：（1）与现有的目标检测器相比，它需要更长的训练轮次才能收敛。例如，在 COCO（Lin et al., 2014）基准上，DETR 需要 500 个 epoch 才能收敛，这比 Faster R-CNN（Ren et al., 2015）慢约 10 到 20 倍。（2）DETR 在检测小物体方面表现相对较低。现代目标检测器通常利用多尺度特征，其中小物体是从高分辨率特征图中检测出来的。同时，高分辨率特征图会导致 DETR 的复杂度变得不可接受。上述问题主要归因于 Transformer 组件在处理图像特征图时的缺陷。在初始化时，注意力模块将几乎均匀的注意力权重投射到特征图中的所有像素上。需要长时间的训练轮次才能学习将注意力权重集中在稀疏的有意义位置上。另一方面，Transformer 编码器中的注意力权重计算相对于像素数量具有二次方计算复杂度。因此，处理高分辨率特征图具有非常高的计算和内存复杂度。

在图像领域，可变形卷积（Deformable convolution, Dai et al., 2017）是一种强大且高效的机制，用于关注稀疏的空间位置。它自然地避免了上述问题。虽然它缺乏元素关系建模机制，但这正是 DETR 成功的关键。

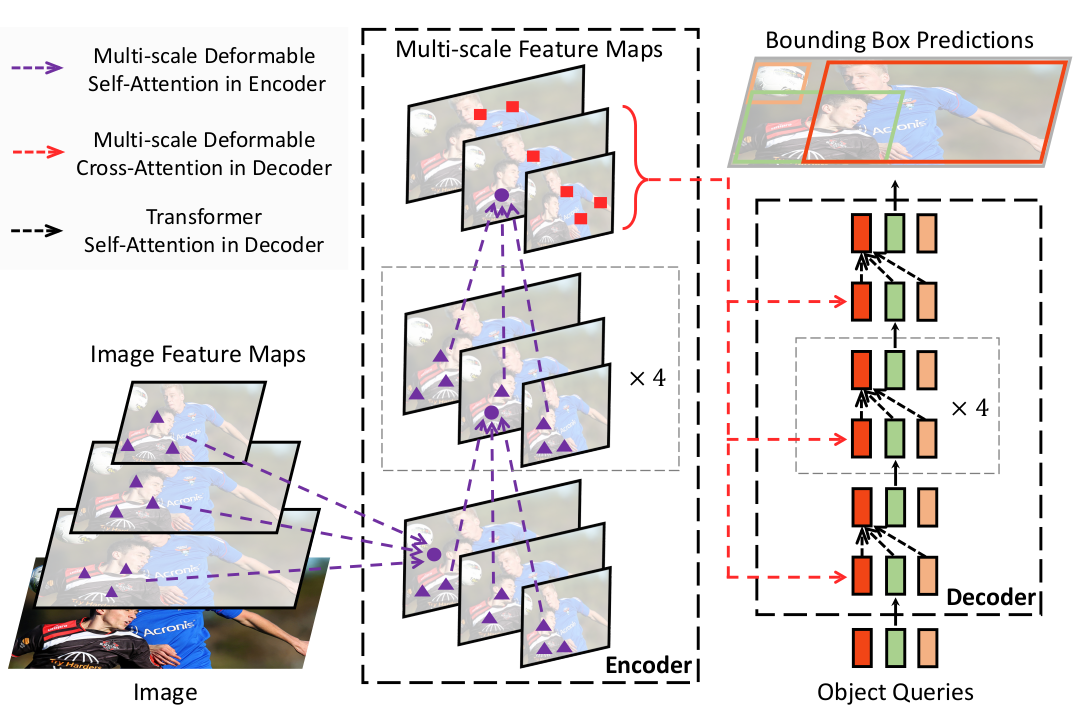
图 1：提出的 Deformable DETR 目标检测器示意图。

在本文中，我们提出了 Deformable DETR ，它缓解了 DETR 收敛慢和复杂度高的问题。它结合了可变形卷积的稀疏空间采样优势和 Transformer 的关系建模能力。我们提出了 可变形注意力模块 (deformable attention module)，它作为预过滤器，从所有特征图像素中关注一小部分采样位置作为突出的关键元素。该模块可以自然地扩展到聚合多尺度特征，而无需 FPN（Lin et al., 2017a）的帮助。在 Deformable DETR 中，我们利用（多尺度）可变形注意力模块来替换处理特征图的 Transformer 注意力模块，如图 1 所示。

Deformable DETR 为我们要开发端到端目标检测器的变体提供了可能性，这得益于其快速收敛以及计算和内存效率。我们探索了一种简单有效的 迭代边界框细化 (iterative bounding box refinement) 机制来提高检测性能。我们还尝试了一种 两阶段 (two-stage) Deformable DETR，其中区域建议（region proposals）也是由 Deformable DETR 的变体生成的，这些建议进一步输入到解码器中进行迭代边界框细化。

在 COCO（Lin et al., 2014）基准上的大量实验证明了我们方法的有效性。与 DETR 相比，Deformable DETR 可以通过减少 10 倍的训练轮次实现更好的性能（特别是在小物体上）。所提出的两阶段 Deformable DETR 变体可以进一步提高性能。代码发布于 https://github.com/fundamentalvision/Deformable-DETR。

高效注意力机制 (Efficient Attention Mechanism)。 Transformers（Vaswani et al., 2017）涉及自注意力和交叉注意力机制。Transformer 最广为人知的担忧之一是在大量关键元素数量下具有高的时间和内存复杂度，这阻碍了模型在许多情况下的可扩展性。最近，许多努力致力于解决这个问题（Tay et al., 2020b），这些大致可以分为三类实践。

第一类是在键（keys）上使用预定义的稀疏注意力模式。最直接的范式是将注意力模式限制在固定的局部窗口中。大多数工作（Liu et al., 2018a; Parmar et al., 2018; Child et al., 2019; Huang et al., 2019; Ho et al., 2019; Wang et al., 2020a; Hu et al., 2019; Ramachandran et al., 2019; Qiu et al., 2019; Beltagy et al., 2020; Ainslie et al., 2020; Zaheer et al., 2020）都遵循这种范式。虽然将注意力模式限制在局部邻域可以降低复杂度，但会丢失全局信息。为了补偿，Child et al. (2019); Huang et al. (2019); Ho et al. (2019); Wang et al. (2020a) 关注固定间隔的关键元素以显著增加键的感受野。Beltagy et al. (2020); Ainslie et al. (2020); Zaheer et al. (2020) 允许少量特殊标记访问所有关键元素。Zaheer et al. (2020); Qiu et al. (2019) 还添加了一些预固定的稀疏注意力模式以直接关注远处的关键元素。

第二类是学习数据依赖的稀疏注意力。Kitaev et al. (2020) 提出了一种基于局部敏感哈希（LSH）的注意力，它将查询（query）和关键（key）元素哈希到不同的桶中。Roy et al. (2020) 提出了类似的想法，其中 k-means 找出最相关的键。Tay et al. (2020a) 学习块排列以实现块状稀疏注意力。

第三类是探索自注意力中的低秩属性。Wang et al. (2020b) 通过在尺寸维度而不是通道维度上的线性投影来减少关键元素的数量。Katharopoulos et al. (2020); Choromanski et al. (2020) 通过核化近似重写了自注意力的计算。

在图像领域，高效注意力机制的设计（例如，Parmar et al. (2018); Child et al. (2019); Huang et al. (2019); Ho et al. (2019); Wang et al. (2020a); Hu et al. (2019); Ramachandran et al. (2019)）仍然仅限于第一类。尽管这在理论上降低了复杂度，但 Ramachandran et al. (2019); Hu et al. (2019) 承认，由于内存访问模式的内在限制，这些方法在实现上比具有相同 FLOPs 的传统卷积慢得多（至少慢 3 倍）。

另一方面，正如 Zhu et al. (2019a) 中讨论的那样，卷积的变体，如可变形卷积（Dai et al., 2017; Zhu et al., 2019b）和动态卷积（Wu et al., 2019），也可以被视为自注意力机制。特别是，可变形卷积在图像识别上的运行比 Transformer 自注意力更有效和高效。同时，它缺乏元素关系建模机制。

我们提出的可变形注意力模块受到可变形卷积的启发，属于第二类。它只关注从查询元素的特征预测出的一小组固定采样点。与 Ramachandran et al. (2019); Hu et al. (2019) 不同，在相同的 FLOPs 下，可变形注意力仅比传统卷积稍慢。

目标检测的多尺度特征表示 (Multi-scale Feature Representation for Object Detection)。 目标检测的主要困难之一是有效地表示巨大不同尺度的物体。现代目标检测器通常利用多尺度特征来适应这一点。作为开创性工作之一，FPN（Lin et al., 2017a）提出了一条自顶向下的路径来结合多尺度特征。PANet（Liu et al., 2018b）进一步在 FPN 之上添加了一条自底向上的路径。Kong et al. (2018) 通过全局注意力操作结合了所有尺度的特征。Zhao et al. (2019) 提出了一个 U 形模块来融合多尺度特征。最近，NAS-FPN（Ghiasi et al., 2019）和 Auto-FPN（Xu et al., 2019）被提出来通过神经架构搜索自动设计跨尺度连接。Tan et al. (2020) 提出了 BiFPN，这是 PANet 的重复简化版本。我们提出的多尺度可变形注意力模块可以自然地通过注意力机制聚合多尺度特征图，而无需这些特征金字塔网络的帮助。

3 重温 TRANSFORMERS 和 DETR (REVISITING TRANSFORMERS AND DETR)

Transformers 中的多头注意力 (Multi-Head Attention in Transformers)。 Transformers (Vaswani et al., 2017) 是一种基于注意力机制的机器翻译网络架构。给定一个查询元素（例如，输出句子中的目标词）和一组关键元素（例如，输入句子中的源词），多头注意力模块 根据测量查询-键对兼容性的注意力权重自适应地聚合关键内容。为了允许模型关注来自不同表示子空间和不同位置的内容，不同注意力头的输出通过可学习的权重线性聚合。设 q∈Ωqq \in \Omega_qq∈Ωq 索引具有表示特征 zq∈RCz_q \in \mathbb{R}^Czq∈RC 的查询元素，并且 k∈Ωkk \in \Omega_kk∈Ωk 索引具有表示特征 xk∈RCx_k \in \mathbb{R}^Cxk∈RC 的关键元素，其中 CCC 是特征维度，Ωq\Omega_qΩq 和 Ωk\Omega_kΩk 分别指定查询和关键元素的集合。那么多头注意力特征计算如下：

MultiHeadAttn(zq,x)=∑m=1MWm[∑k∈ΩkAmqk⋅Wm′xk],(1) \text{MultiHeadAttn}(z_q, x) = \sum_{m=1}^{M} W_m \Big[ \sum_{k \in \Omega_k} A_{mqk} \cdot W'_m x_k \Big], \quad (1) MultiHeadAttn(zq,x)=m=1∑MWm[k∈Ωk∑Amqk⋅Wm′xk],(1)

其中 mmm 索引注意力头，Wm′∈RCv×CW'm \in \mathbb{R}^{C_v \times C}Wm′∈RCv×C 和 Wm∈RC×CvW_m \in \mathbb{R}^{C \times C_v}Wm∈RC×Cv 是可学习的权重（默认 Cv=C/MC_v = C/MCv=C/M）。注意力权重 Amqk∝exp⁡{zqTUmTVmxkCv}A{mqk} \propto \exp \{ \frac{z_q^T U_m^T V_m x_k}{\sqrt{C_v}} \}Amqk∝exp{Cv zqTUmTVmxk} 被归一化为 ∑k∈ΩkAmqk=1\sum_{k \in \Omega_k} A_{mqk} = 1∑k∈ΩkAmqk=1，其中 Um,Vm∈RCv×CU_m, V_m \in \mathbb{R}^{C_v \times C}Um,Vm∈RCv×C 也是可学习的权重。为了消除不同空间位置的歧义，表示特征 zqz_qzq 和 xkx_kxk 通常是元素内容和位置嵌入的串联/求和。

Transformers 存在两个已知问题。一是 Transformers 需要很长的训练计划才能收敛。假设查询和关键元素的数量分别为 NqN_qNq 和 NkN_kNk。通常，通过适当的参数初始化，UmzqU_m z_qUmzq 和 VmxkV_m x_kVmxk 服从均值为 0 方差为 1 的分布，这使得当 NkN_kNk 很大时，注意力权重 Amqk≈1NkA_{mqk} \approx \frac{1}{N_k}Amqk≈Nk1。这将导致输入特征的梯度模糊。因此，需要长时间的训练计划，以便注意力权重可以集中在特定的键上。在图像领域，关键元素通常是图像像素，NkN_kNk 可能非常大，收敛非常缓慢。

另一方面，对于大量的查询和关键元素，多头注意力的计算和内存复杂度可能非常高。公式 1 的计算复杂度为 O(NqC2+NkC2+NqNkC)O(N_q C^2 + N_k C^2 + N_q N_k C)O(NqC2+NkC2+NqNkC)。在图像领域，当查询和关键元素都是像素时，Nq=Nk≫CN_q = N_k \gg CNq=Nk≫C，复杂度由第三项主导，即 O(NqNkC)O(N_q N_k C)O(NqNkC)。因此，多头注意力模块随特征图大小呈二次方复杂度增长。

DETR. DETR (Carion et al., 2020) 建立在 Transformer 编码器-解码器架构之上，结合了基于集合的匈牙利损失（Hungarian loss），通过二分匹配强制每个真实边界框有唯一的预测。我们简要回顾其网络架构如下。

给定由 CNN 主干（例如 ResNet (He et al., 2016)）提取的输入特征图 x∈RC×H×Wx \in \mathbb{R}^{C \times H \times W}x∈RC×H×W，DETR 利用标准的 Transformer 编码器-解码器架构将输入特征图转换为一组对象查询的特征。一个 3 层前馈神经网络（FFN）和一个线性投影被添加到对象查询特征（由解码器产生）之上作为检测头。FFN 充当回归分支以预测边界框坐标 b∈[0,1]4b \in [0, 1]^4b∈[0,1]4，其中 b={bx,by,bw,bh}b = \{b_x, b_y, b_w, b_h\}b={bx,by,bw,bh} 编码归一化的框中心坐标、框高度和宽度（相对于图像大小）。线性投影充当分类分支以产生分类结果。

对于 DETR 中的 Transformer 编码器，查询和关键元素都是特征图中的像素。输入是 ResNet 特征图（带有编码的位置嵌入）。设 HHH 和 WWW 分别表示特征图的高度和宽度。自注意力的计算复杂度为 O(H2W2C)O(H^2 W^2 C)O(H2W2C)，随空间大小呈二次方增长。

对于 DETR 中的 Transformer 解码器，输入包括来自编码器的特征图和由可学习位置嵌入表示的 NNN 个对象查询（例如，N=100N = 100N=100）。解码器中有两种类型的注意力模块，即交叉注意力和自注意力模块。在交叉注意力模块中，对象查询从特征图中提取特征。查询元素是对象查询，关键元素是来自编码器的输出特征图。其中，Nq=N,Nk=H×WN_q = N, N_k = H \times WNq=N,Nk=H×W，交叉注意力的复杂度为 O(HWC2+NHWC)O(HW C^2 + NHW C)O(HWC2+NHWC)。复杂度随特征图的空间大小线性增长。在自注意力模块中，对象查询相互交互以捕获它们的关系。查询和关键元素都是对象查询。其中，Nq=Nk=NN_q = N_k = NNq=Nk=N，自注意力模块的复杂度为 O(2NC2+N2C)O(2NC^2 + N^2C)O(2NC2+N2C)。对于适量的对象查询，复杂度是可以接受的。

DETR 是目标检测的一种有吸引力的设计，它消除了对许多手工设计组件的需求。然而，它也有自己的问题。这些问题主要归因于 Transformer 注意力在处理图像特征图作为关键元素时的缺陷：（1）DETR 在检测小物体方面性能相对较低。现代目标检测器使用高分辨率特征图来更好地检测小物体。然而，高分辨率特征图会导致 DETR 转换器编码器中的自注意力模块产生不可接受的复杂度，其具有随输入特征图空间大小的二次方复杂度。（2）与现代目标检测器相比，DETR 需要更多的训练轮次才能收敛。这主要是因为处理图像特征的注意力模块很难训练。例如，在初始化时，交叉注意力模块几乎是对整个特征图的平均关注。而在训练结束时，注意力图被学习为非常稀疏，仅关注对象的极端部分。DETR 似乎需要很长的训练计划来学习注意力图中的这种显著变化。

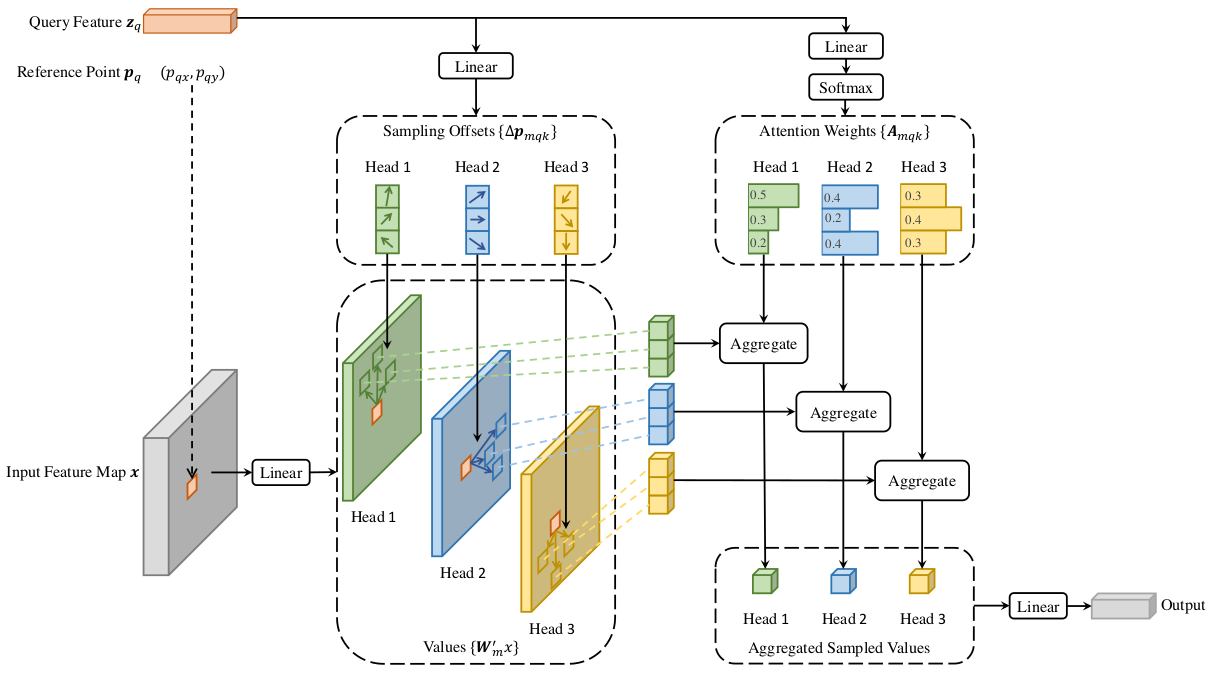
图 2：提出的可变形注意力模块图解

4 方法 (METHOD)

4.1 用于端到端目标检测的可变形 TRANSFORMERS

可变形注意力模块 (Deformable Attention Module)。 将 Transformer 注意力应用于图像特征图的核心问题是它会查看所有可能的空间位置。为了解决这个问题，我们提出了一个 可变形注意力模块。受可变形卷积（Dai et al., 2017; Zhu et al., 2019b）的启发，可变形注意力模块仅关注参考点周围的一小组关键采样点，无论特征图的空间大小如何，如图 2 所示。通过为每个查询仅分配少量固定数量的键，可以缓解收敛和特征空间分辨率的问题。

给定输入特征图 x∈RC×H×Wx \in \mathbb{R}^{C \times H \times W}x∈RC×H×W，设 qqq 索引具有内容特征 zqz_qzq 和二维参考点 pqp_qpq 的查询元素，可变形注意力特征计算如下：

DeformAttn(zq,pq,x)=∑m=1MWm[∑k=1KAmqk⋅Wm′x(pq+Δpmqk)],(2) \text{DeformAttn}(z_q, p_q, x) = \sum_{m=1}^{M} W_m \Big[ \sum_{k=1}^{K} A_{mqk} \cdot W'm x(p_q + \Delta p{mqk}) \Big], \quad (2) DeformAttn(zq,pq,x)=m=1∑MWm[k=1∑KAmqk⋅Wm′x(pq+Δpmqk)],(2)

其中 mmm 索引注意力头，kkk 索引采样键，KKK 是总采样键数（K≪HWK \ll HWK≪HW）。Δpmqk\Delta p_{mqk}Δpmqk 和 AmqkA_{mqk}Amqk 分别表示第 mmm 个注意力头中第 kkk 个采样点的采样偏移和注意力权重。标量注意力权重 AmqkA_{mqk}Amqk 位于 [0,1][0, 1][0,1] 范围内，归一化为 ∑k=1KAmqk=1\sum_{k=1}^{K} A_{mqk} = 1∑k=1KAmqk=1。Δpmqk∈R2\Delta p_{mqk} \in \mathbb{R}^2Δpmqk∈R2 是具有无约束范围的二维实数。由于 pq+Δpmqkp_q + \Delta p_{mqk}pq+Δpmqk 是分数，因此如 Dai et al. (2017) 中那样应用双线性插值来计算 x(pq+Δpmqk)x(p_q + \Delta p_{mqk})x(pq+Δpmqk)。Δpmqk\Delta p_{mqk}Δpmqk 和 AmqkA_{mqk}Amqk 都是通过对查询特征 zqz_qzq 进行线性投影获得的。在实现中，查询特征 zqz_qzq 被送入一个 3MK3MK3MK 通道的线性投影算子，其中前 2MK2MK2MK 个通道编码采样偏移 Δpmqk\Delta p_{mqk}Δpmqk，剩余的 MKMKMK 个通道被送入 softmax 算子以获得注意力权重 AmqkA_{mqk}Amqk。

可变形注意力模块旨在处理卷积特征图作为关键元素。设 NqN_qNq 为查询元素的数量，当 MKMKMK 相对较小时，可变形注意力模块的复杂度为 O(2NqC2+min⁡(HWC2,NqKC2))O(2N_q C^2 + \min(HWC^2, N_q K C^2))O(2NqC2+min(HWC2,NqKC2))（详见附录 A.1）。当应用于 DETR 编码器时，其中 Nq=HWN_q = HWNq=HW，复杂度变为 O(HWC2)O(HWC^2)O(HWC2)，与空间大小呈线性复杂度。当用作交叉注意力模块在 DETR 解码器中，其中 Nq=NN_q = NNq=N（NNN 是对象查询的数量），复杂度变为 O(NKC2)O(NKC^2)O(NKC2)，与空间大小 HWHWHW 无关。

多尺度可变形注意力模块 (Multi-scale Deformable Attention Module)。 大多数现代目标检测框架受益于多尺度特征图（Liu et al., 2020）。我们提出的可变形注意力模块可以自然地扩展到多尺度特征图。

设 {xl}l=1L\{x^l\}_{l=1}^{L}{xl}l=1L 为输入的多尺度特征图，其中 xl∈RC×Hl×Wlx^l \in \mathbb{R}^{C \times H_l \times W_l}xl∈RC×Hl×Wl。设 p^q∈[0,1]2\hat{p}_q \in [0, 1]^2p^q∈[0,1]2 为每个查询元素 qqq 的参考点的归一化坐标，则多尺度可变形注意力模块应用如下：

MSDeformAttn(zq,p^q,{xl}l=1L)=∑m=1MWm[∑l=1L∑k=1KAmlqk⋅Wm′xl(ϕl(p^q)+Δpmlqk)],(3) \text{MSDeformAttn}(z_q, \hat{p}q, \{x^l\}{l=1}^{L}) = \sum_{m=1}^{M} W_m \Big[ \sum_{l=1}^{L} \sum_{k=1}^{K} A_{mlqk} \cdot W'_m x^l(\phi_l(\hat{p}q) + \Delta p{mlqk}) \Big], \quad (3) MSDeformAttn(zq,p^q,{xl}l=1L)=m=1∑MWm[l=1∑Lk=1∑KAmlqk⋅Wm′xl(ϕl(p^q)+Δpmlqk)],(3)

其中 mmm 索引注意力头，lll 索引输入特征层级，kkk 索引采样点。Δpmlqk\Delta p_{mlqk}Δpmlqk 和 AmlqkA_{mlqk}Amlqk 分别表示第 mmm 个注意力头在第 lll 个特征层级中的第 kkk 个采样点的采样偏移和注意力权重。标量注意力权重 AmlqkA_{mlqk}Amlqk 归一化为 ∑l=1L∑k=1KAmlqk=1\sum_{l=1}^{L} \sum_{k=1}^{K} A_{mlqk} = 1∑l=1L∑k=1KAmlqk=1。这里，为了尺度公式的清晰性，我们使用归一化坐标 p^q∈[0,1]2\hat{p}_q \in [0, 1]^2p^q∈[0,1]2，其中归一化坐标 (0,0)(0, 0)(0,0) 和 (1,1)(1, 1)(1,1) 分别表示左上角和右下角图像角点。公式 3 中的函数 ϕl(p^q)\phi_l(\hat{p}_q)ϕl(p^q) 将归一化坐标 p^q\hat{p}_qp^q 重新缩放到第 lll 层级的输入特征图。多尺度可变形注意力与之前的单尺度版本非常相似，只是它从多尺度特征图中采样 LKLKLK 个点，而不是从单尺度特征图中采样 KKK 个点。

当 L=1,K=1L=1, K=1L=1,K=1 且 Wm′∈RCv×CW'_m \in \mathbb{R}^{C_v \times C}Wm′∈RCv×C 固定为单位矩阵时，所提出的注意力模块将退化为可变形卷积（Dai et al., 2017）。可变形卷积专为单尺度输入设计，每个注意力头仅关注一个采样点。然而，我们的多尺度可变形注意力在多尺度输入中查看多个采样点。提出的（多尺度）可变形注意力模块也可以被视为 Transformer 注意力的一种高效变体，其中由可变形采样位置引入了预过滤机制。当采样点遍历所有可能位置时，提出的注意力模块等同于 Transformer 注意力。

可变形 Transformer 编码器 (Deformable Transformer Encoder)。 我们用提出的多尺度可变形注意力模块替换 DETR 中处理特征图的 Transformer 注意力模块。编码器的输入和输出都是具有相同分辨率的多尺度特征图。在编码器中，我们从 ResNet（He et al., 2016）的阶段 C3C_3C3 到 C5C_5C5 的输出特征图中提取多尺度特征图 {xl}l=1L−1\{x^l\}_{l=1}^{L-1}{xl}l=1L−1 (L=4L=4L=4)（通过 1×11 \times 11×1 卷积转换），其中 ClC_lCl 的分辨率比输入图像低 2l2^l2l。最低分辨率特征图 xLx^LxL 是通过在最终 C5C_5C5 阶段上的 3×33 \times 33×3 步幅 2 卷积获得的，表示为 C6C_6C6。所有多尺度特征图都具有 C=256C=256C=256 个通道。注意，不使用 FPN（Lin et al., 2017a）中的自顶向下结构，因为我们提出的多尺度可变形注意力本身可以在多尺度特征图之间交换信息。附录 A.2 中也说明了多尺度特征图的构建。第 5.2 节的实验表明添加 FPN 不会提高性能。

在编码器中应用多尺度可变形注意力模块时，输出是与输入分辨率相同的多尺度特征图。键和查询元素都是来自多尺度特征图的像素。对于每个查询像素，参考点是其自身。为了识别每个查询像素位于哪个特征层级，除了位置嵌入外，我们还在特征表示中添加了一个尺度层级嵌入，表示为 ele_lel。与具有固定编码的位置嵌入不同，尺度层级嵌入 {el}l=1L\{e_l\}_{l=1}^{L}{el}l=1L 是随机初始化并与网络联合训练的。

可变形 Transformer 解码器 (Deformable Transformer Decoder)。 解码器中有交叉注意力和自注意力模块。两种类型注意力模块的查询元素都是对象查询。在交叉注意力模块中，对象查询从特征图中提取特征，其中关键元素是来自编码器的输出特征图。在自注意力模块中，对象查询相互交互，其中关键元素是对象查询。由于我们提出的可变形注意力模块设计用于处理卷积特征图作为关键元素，我们仅将每个交叉注意力模块替换为多尺度可变形注意力模块，而保持自注意力模块不变。对于每个对象查询，参考点的二维归一化坐标参考点 p^q\hat{p}_qp^q 是通过可学习的线性投影和 sigmoid 函数从其对象查询嵌入中预测出来的。

由于多尺度可变形注意力模块提取参考点周围的图像特征，我们让检测头预测边界框为相对于参考点的相对偏移，以进一步降低优化难度。参考点用作框中心的初始猜测。检测头预测相对于参考点的相对偏移。详情请查看附录 A.3。这样，学习到的解码器注意力将与预测的边界框有很强的相关性，这也加速了训练收敛。

通过在 DETR 中用可变形注意力模块替换 Transformer 注意力模块，我们建立了一个高效且快速收敛的检测系统，称为 Deformable DETR（见图 1）。

4.2 Deformable DETR 的额外改进和变体

Deformable DETR 为我们利用端到端目标检测器的各种变体提供了可能性，这得益于其快速收敛以及计算和内存效率。由于篇幅有限，我们仅在此介绍这些改进和变体的核心思想。实施细节见附录 A.4。

迭代边界框细化 (Iterative Bounding Box Refinement)。 这受到光流估计中开发的迭代细化的启发（Teed & Deng, 2020）。我们建立了一种简单有效的迭代边界框细化机制来提高检测性能。在这里，每个解码器层根据前一层的预测来细化边界框。

两阶段 Deformable DETR (Two-Stage Deformable DETR)。 在原始 DETR 中，解码器中的对象查询与当前图像无关。受两阶段目标检测器的启发，我们探索了 Deformable DETR 的一种变体，用于生成区域建议（region proposals）作为第一阶段。生成的区域建议将被送入解码器作为对象查询以进行进一步细化，形成两阶段 Deformable DETR。

在第一阶段，为了实现高召回率的建议，多尺度特征图中的每个像素都将作为一个对象查询。然而，直接将对象查询设置为像素会给解码器中的自注意力模块带来不可接受的计算和内存成本，其复杂度随查询数量呈二次方增长。为了避免这个问题，我们移除了解码器，并形成了一个仅包含编码器的 Deformable DETR 用于区域建议生成。在其中，每个像素被分配为一个对象查询，直接预测一个边界框。选取得分最高的边界框作为区域建议。在将区域建议送入第二阶段之前不应用 NMS。

5 实验 (EXPERIMENT)

数据集。 我们在 COCO 2017 数据集（Lin et al., 2014）上进行实验。我们的模型在 train 集合上训练，并在 val 集合和 test-dev 集合上评估。

实施细节。 ImageNet（Deng et al., 2009）预训练的 ResNet-50（He et al., 2016）被用作消融实验的主干。提取多尺度特征图时不使用 FPN（Lin et al., 2017a）。默认情况下，M=8M=8M=8 和 K=4K=4K=4 设置用于可变形注意力。可变形 Transformer 编码器的参数在不同特征层级之间共享。其他超参数设置和训练策略主要遵循 DETR（Carion et al., 2020），除了使用 Focal Loss（Lin et al., 2017b）（损失权重为 2）用于边界框分类，并且对象查询的数量从 100 增加到 300。我们也报告了经过这些修改的 DETR-DC5 的性能以便公平比较，记为 DETR-DC5+^++。默认情况下，模型训练 50 个 epoch，学习率在第 40 个 epoch 衰减 0.1 倍。遵循 DETR（Carion et al., 2020），我们使用 Adam 优化器（Kingma & Ba, 2015）训练我们的模型，基础学习率为 2×10−4,β1=0.9,β2=0.9992 \times 10^{-4}, \beta_1=0.9, \beta_2=0.9992×10−4,β1=0.9,β2=0.999，权重衰减为 10−410^{-4}10−4。用于预测对象查询参考点和采样偏移的线性投影的学习率乘以 0.1 倍。运行时间在 NVIDIA Tesla V100 GPU 上评估。

5.1 与 DETR 的比较

如表 1 所示，与 Faster R-CNN + FPN 相比，DETR 需要更多的训练轮次才能收敛，并且在检测小物体方面性能较低。与DETR相比，Deformable DETR 仅用 10 倍少的训练轮次就实现了更好的性能（特别是在小物体上）。详细的收敛曲线如图 3 所示。借助迭代边界框细化和两阶段范式，我们的方法可以进一步提高检测精度。

我们提出的 Deformable DETR 在 FLOPs 上与 Faster R-CNN + FPN 和 DETR-DC5 相当。但运行速度比 DETR-DC5 快得多（1.6 倍），仅比 Faster R-CNN + FPN 慢 25%。DETR-DC5 的速度问题主要是由于 Transformer 注意力中有大量的内存访问。我们提出的可变形注意力可以缓解这个问题，代价是无序的内存访问。因此，它仍然比传统卷积慢一点。

表 1：Deformable DETR 与 DETR 在 COCO 2017 val 集上的比较。 DETR-DC5+^++ 表示具有 Focal Loss 和 300 个对象查询的 DETR-DC5。

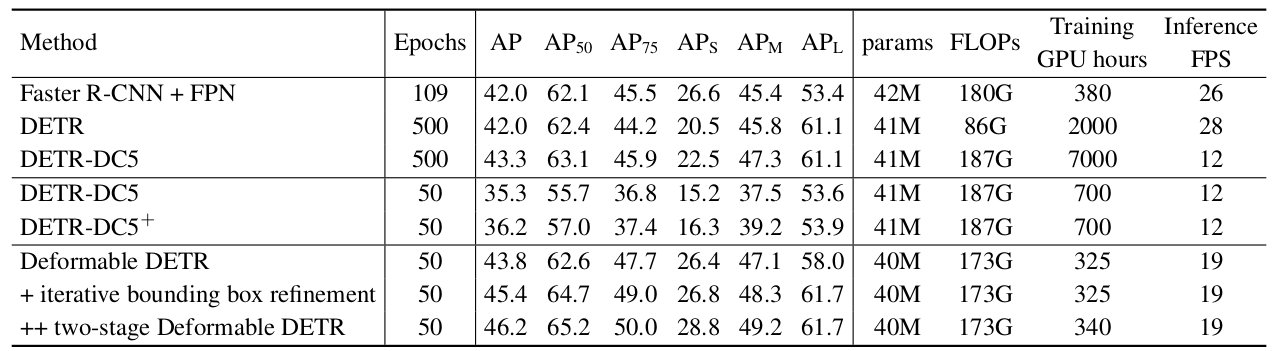
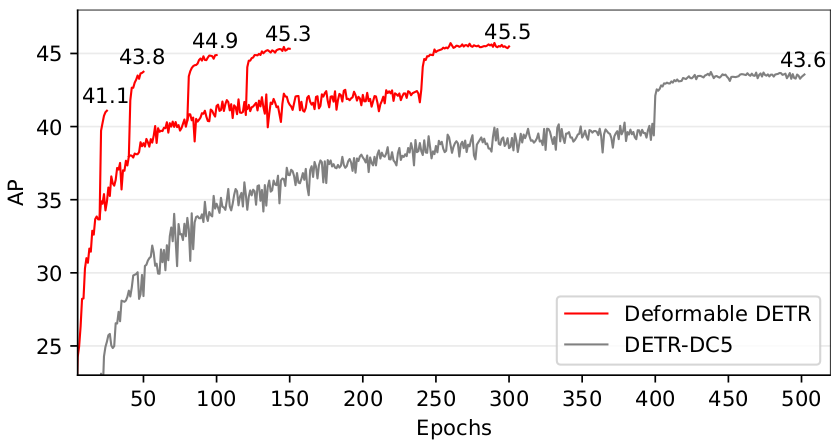
图 3：Deformable DETR 和 DETR-DC5 在 COCO 2017 val 集上的收敛曲线。 对于 Deformable DETR，我们通过改变降低学习率的 epoch（AP 分数跃升处）来探索不同的训练计划。

5.2 可变形注意力的消融研究

表 2 展示了所提出的可变形注意力模块的各种设计选择的消融实验。使用多尺度输入代替单尺度输入可以有效提高检测精度，AP 提高 1.7%，特别是在小物体上提高 2.9% APS_SS。增加采样点数量 KKK 可以进一步提高 0.9% AP。使用多尺度可变形注意力（允许不同尺度层级之间的信息交换）可以带来额外的 1.5% AP 提升。由于已经采用了跨层级特征交换，添加 FPN 不会提高性能。当不应用多尺度注意力且 K=1K=1K=1 时，我们的（多尺度）可变形注意力模块退化为可变形卷积，其精度明显较低。

5.3 与最先进方法的比较

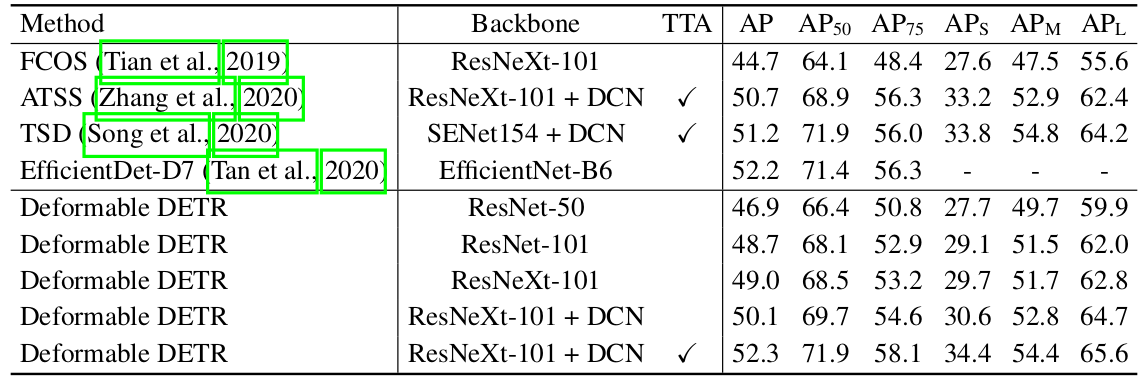
表 3 将所提出的方法与其他最先进的方法进行了比较。我们的模型在表 3 中同时利用了迭代边界框细化和两阶段机制。使用 ResNet-101 和 ResNeXt-101 (Xie et al., 2017)，我们的方法在没有任何额外技巧的情况下分别达到了 48.7 AP 和 49.0 AP。通过使用 ResNeXt-101 和 DCN (Zhu et al., 2019b)，精度上升到 50.1 AP。通过额外的测试时间增强（TTA），所提出的方法达到了 52.3 AP。

表 2：COCO 2017 val 集上可变形注意力的消融实验。 "MS inputs" 表示使用多尺度输入。"MS attention" 表示使用多尺度可变形注意力。KKK 是每个特征层级上每个注意力头的采样点数量。

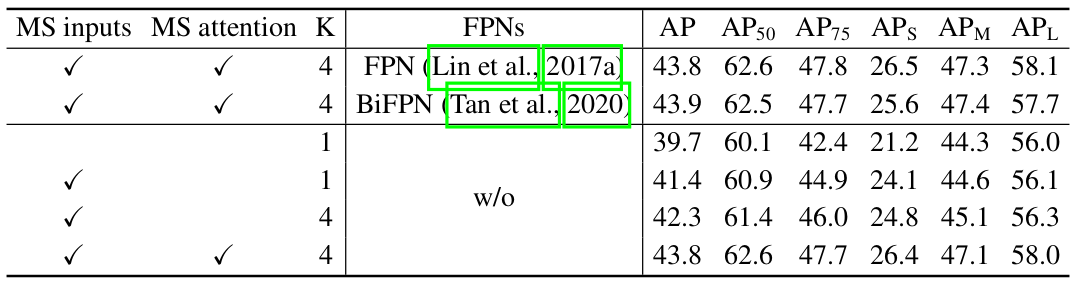
表 3：Deformable DETR 与最先进方法在 COCO 2017 test-dev 集上的比较。 "TTA" 表示包括水平翻转和多尺度测试在内的测试时间增强。

6 结论 (CONCLUSION)

Deformable DETR 是一种端到端的目标检测器，高效且收敛速度快。它使我们能够探索更多有趣和实用的端到端目标检测器变体。Deformable DETR 的核心是（多尺度）可变形注意力模块，这是一种处理图像特征图的高效注意力机制。我们希望我们的工作能为探索端到端目标检测开辟新的可能性。