线代第二章矩阵第八节逆矩阵、解矩阵方程

一、逆矩阵

逆矩阵是针对方阵定义的核心概念。

1. 定义

对于 n 阶方阵 A，若存在一个 n 阶方阵 B，满足

其中 E 是 n 阶单位矩阵，则称 A 可逆 （或非奇异矩阵），并称 B 是 A 的逆矩阵，记作 。

注：可逆矩阵的逆矩阵是唯一的。

2. 可逆的充要条件

n 阶方阵 A 可逆 ⟺ （行列式不为 0） ⟺ r(A)=n（满秩）。

3. 逆矩阵的计算方法

方法 1：伴随矩阵法（理论核心，适合低阶方阵）

由伴随矩阵的核心恒等式 ，推导得逆矩阵公式：

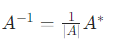
二、解矩阵方程

矩阵方程的基本形式为 AX=B、XA=B、AXB=C，核心解法是利用逆矩阵的消去性，前提是对应矩阵可逆。

1. 基本形式及解法

方程形式	可逆条件	求解公式	核心思路
AX=B	A 可逆	X=B	两边左乘 ：AX=B⟹EX=B
XA=B	A 可逆	X=B	两边右乘 ：XA=B⟹XE=B
AXB=C	A,B 均可逆	X=C	左乘 、右乘 ：AXB=C

关键注意 ：矩阵乘法不满足交换律，左乘和右乘不能混淆！

2. 求解步骤（以 AX=B 为例）

1. 判断 A 是否可逆：计算 ∣A∣，若 ∣A∣0，则可逆；
2. 计算 （伴随矩阵法或初等行变换法）；
3. 计算乘积 B，得到 X。

3. 初等行变换法直接求解 AX=B（更高效）

无需单独计算 ，直接构造增广矩阵 A∣B，对其进行初等行变换 ，当左边 A 化为 E 时，右边 B 同步化为 B，即A∣B初等行变换​E∣B=E∣X

4. 特殊情况：A 不可逆时

若 A 不可逆（∣A∣=0），则不能用逆矩阵法，需将矩阵方程转化为线性方程组，通过高斯消元法判断是否有解、求解通解。

内容来源-B站宋浩老师