SLAM文献之-Embedding Manifold Structures into Kalman Filters（3)

VII. 实验

在本节中，我们将把所开发的 Kalman 滤波框架与工具包实现应用于来自文献 [15] 的 紧耦合激光雷达--惯性导航系统 。整体系统如图 9 所示，包括：

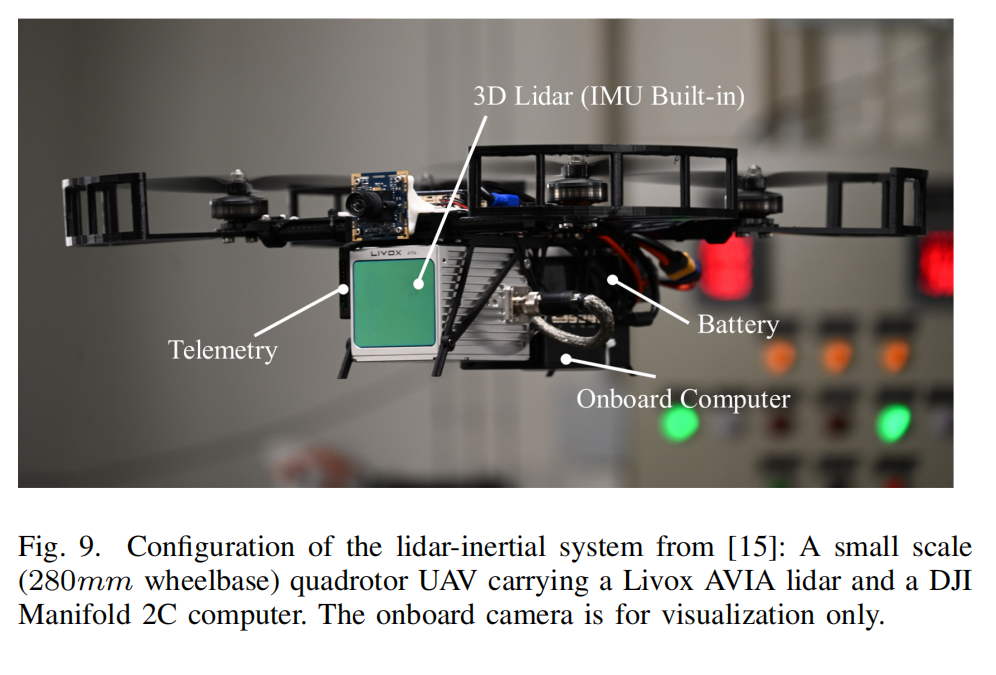
一台固态激光雷达（Livox AVIA，内置 IMU）
一个机载计算机

该激光雷达提供 10 Hz 的扫描频率 和 200 Hz 的陀螺仪与加速度计测量 。与常规旋转式激光雷达（如 Velodyne 系列）不同，Livox AVIA 的视场（FoV）仅为 70° ，这使得激光雷达--惯性里程计任务更具挑战性。

机载计算机配置为：1.8 GHz 四核 Intel i7-8550U CPU + 8GB RAM 。

除了 [15] 中原始的状态估计问题外，我们进一步加入 激光雷达与 IMU 之间外参的在线估计。

A. 系统建模

设：

全局坐标系为 G（即 IMU 的初始坐标）
IMU 坐标系为 I（即机体系）
激光雷达坐标系为 L

假设激光雷达刚性安装在 IMU 上，其外参为：

I T L = ( I R L , I p L ) {}^{I}T_{L} = \left({}^{I}R_{L}, {}^{I}p_{L}\right) ITL=(IRL,IpL)

系统的目标是估计：

IMU 的位置 , G p I , ,{}^{G}p_I , ,GpI,、速度 , G v I , ,{}^{G}v_I , ,GvI,、姿态 , G R I ∈ S O ( 3 ) , {}^{G}R_I \in SO(3) ,GRI∈SO(3)
IMU 的零偏 b a , b ω b_a, b_\omega ba,bω
全局坐标系中的重力向量 , G g ,{}^{G}g ,Gg
激光雷达--IMU 外参 , I T L = ( I R L , I p L ) ,{}^{I}T_L = \left({}^{I}R_L, {}^{I}p_L\right) ,ITL=(IRL,IpL) 的在线估计
构建全局点云地图

在文献 [15] 的状态表达基础上加入激光雷达--IMU 外参，我们得到如下系统模型：

状态方程

G p ˙ I = G v I , G v ˙ I = G R I ( a m − b a − n a ) + G g G R ˙ I = G R I ( ω m − b ω − n ω ) ∧ b ˙ ω = n b ω , b ˙ a = n b a G g ˙ = 0 , I R ˙ L = 0 , I p ˙ L = 0 (52) \begin{aligned} {}^{G}\dot{p}I &= {}^{G}v_I , \ {}^{G}\dot{v}I &= {}^{G}R_I (a_m - b_a - n_a) + {}^{G}g\ \\ {}^{G}\dot{R}I &= {}^{G}R_I(\omega_m - b\omega - n\omega)^\wedge \ \dot{b}\omega &= n_{b_\omega}, \ \dot{b}a &= n{b_a}\\ {}^{G}\dot{g} &= 0, \ {}^{I}\dot{R}_L &= 0, \ {}^{I}\dot{p}_L &= 0 \end{aligned} \tag{52} Gp˙IGR˙IGg˙=GvI, Gv˙I=GRI(ωm−bω−nω)∧ b˙ω=0, IR˙L=GRI(am−ba−na)+Gg =nbω, b˙a=0, Ip˙L=nba=0(52)

其中：

a m , ω m a_m,\ \omega_m am, ωm 为 IMU 的加速度计与陀螺仪测量
n a , n ω n_a,\ n_\omega na, nω 为 IMU 噪声
n b ω , n b a n_{b_\omega},\ n_{b_a} nbω, nba 为驱动零偏的高斯白噪声
重力向量 , G g , ,{}^{G}g, ,Gg, 长度固定为 9.81 , m/s 2 9.81,\text{m/s}^2 9.81,m/s2

测量模型

测量模型与文献 [15] 完全一致：对新的激光雷达扫描，首先基于局部曲率 [36] 提取 平面点 和 边缘点（即特征点）。

对于测得的每个特征点 , L ! p i f , i = 1 , ... , m ,{}^{L}!p^f_i,\ i=1,\dots,m ,L!pif, i=1,...,m，其在全局坐标系中的真实位置应落在地图中对应的平面（或边缘）上。

地图中对应的特征由：

平面的法向量（或边缘方向） u i u_i ui
平面（或边缘）上一点 , G q i ,{}^{G}q_i ,Gqi

表示。

由于特征点是在激光雷达坐标系中测得，并带有测量噪声 n i n_i ni，其在全局坐标系中的真实位置应为：

G T I I T L ( L p i f − n i ) {}^{G}T_I {}^{I}T_L \left({}^{L}p^f_i - n_i\right) GTIITL(Lpif−ni)

因为该真实点位于由 u i , G q i u_i,{}^{G}q_i ui,Gqi 所定义的平面（或边缘）上，其到该平面的距离应为零：

G i ( G T I I T L ( p i f − n i ) − G q i ) = 0 , i = 1 , ... , m (53) G_i\left( {}^{G}T_I {}^{I}T_L\left(p^f_i - n_i\right) - {}^{G}q_i \right) = 0, \qquad i = 1,\dots,m \tag{53} Gi(GTIITL(pif−ni)−Gqi)=0,i=1,...,m(53)

其中：

若为平面特征， G i = u i ⊤ G_i = u_i^\top Gi=ui⊤
若为边缘特征， G i G_i Gi = ⌊ {\lfloor} ⌊ u i ⌋ u_i{\rfloor} ui⌋

此方程定义了隐式测量模型，关联测量 , L p i f ,{}^{L}p^f_i ,Lpif、噪声 n i n_i ni、以及真实状态 , G T I ,{}^{G}T_I ,GTI 与 , I T L ,{}^{I}T_L ,ITL。

特征关联与地图更新

为了从地图中获得对应的 u i u_i ui 与 , G q i ,{}^{G}q_i ,Gqi：

使用 当前迭代的状态估计 将特征点 , L p i f ,{}^{L}p^f_i ,Lpif 投影到全局坐标系；
在当前地图中寻找 距离最近的 5 个同类特征点；
在迭代 Kalman 滤波收敛后，使用更新后的最优状态将特征点投影到全局坐标系；
将该点加入地图；
下一次扫描时，使用更新后的地图进行配准。

B. 规范表达（Canonical representation）

利用第 IV 节中描述的零阶保持（Zero-order Hold, ZOH）离散化方法，可以将具有状态模型（52）和测量模型（53）的系统离散化，并写成如下的规范形式（canonical form）：

状态空间与测量空间

S = R 3 × R 3 × S O ( 3 ) × R 3 × R 3 × S 2 × S O ( 3 ) × R 3 , S = \mathbb{R}^3 \times \mathbb{R}^3 \times SO(3) \times \mathbb{R}^3 \times \mathbb{R}^3 \times S^2 \times SO(3) \times \mathbb{R}^3, S=R3×R3×SO(3)×R3×R3×S2×SO(3)×R3,

M = R 1 × ⋯ × R 1 ⏟ m , M = \underbrace{ \mathbb{R}^1 \times \cdots \times \mathbb{R}^1 }_{m\ \text{}}, M=m R1×⋯×R1,

系统变量表示

x T = [ G p I G v I G R I b a b ω G g I R L I p L ] , x^T = \begin{bmatrix} {}^{G}p_I & {}^{G}v_I & {}^{G}R_I & b_a & b_\omega & {}^{G}g & {}^{I}R_L & {}^{I}p_L \end{bmatrix}, xT=[GpIGvIGRIbabωGgIRLIpL],

u T = [ a m ω m ] u^T = \begin{bmatrix} a_m & \omega_m \end{bmatrix} uT=[amωm]

系统状态方程（离散化后的系统函数）

f ( x , u , w ) T = [ G v I G R I ( a m − b a − n a ) + G g ω m − b ω − n ω n b a n b ω 0 0 0 ] , f(x, u, w)^T = \begin{bmatrix} {}^{G}v_I \ {}^{G}R_I (a_m - b_a - n_a) + {}^{G}g \ \omega_m - b_\omega - n_\omega \ n_{b_a} \ n_{b_\omega} \ 0 \ 0 \ 0 \end{bmatrix}, f(x,u,w)T=[GvI GRI(am−ba−na)+Gg ωm−bω−nω nba nbω 0 0 0],

测量模型（第 i 个特征点）

h i ( x , v ) T = G i ( G T I I T L ( L p i f − n i ) − G q i ) , (54) h_i(x, v)^T = G_i\left( {}^{G}T_I{}^{I}T_L ( {}^{L}p^f_i - n_i ) - {}^{G}q_i \right), \tag{54} hi(x,v)T=Gi(GTIITL(Lpif−ni)−Gqi),(54)

w T = [ n a n ω n b a n b ω ] , v T = [ ⋯ n i ⋯ ] , i = 1 , ... , m . w^T = \begin{bmatrix} n_a & n_\omega & n_{b_a} & n_{b_\omega} \end{bmatrix},\\ \qquad v^T = \begin{bmatrix} \cdots\ n_i\ \cdots \end{bmatrix},\quad i=1,\dots,m. wT=[nanωnbanbω],vT=[⋯ ni ⋯],i=1,...,m.

由于测量模型输出恒为零，因此可认为等效测量 z z z 恒为 0。

系统特定的偏导数（System-specific partial differentiations）

1. 对状态的偏导

∂ f ( x ⊞ δ x , u , 0 ) ∂ δ x ∣ δ x = 0 [ 0 I 0 0 0 0 0 0 0 0 U 23 F − G R I 0 U 26 F 0 0 0 0 0 0 − I 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] (55a) \frac{\partial f(x \boxplus \delta x, u, 0)}{\partial \delta x}\bigg|{\delta x=0} \begin{bmatrix} 0 & I & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & U^{F}{23} & - {}^{G}R_I & 0 & U^{F}_{26} & 0 & 0 \\ 0 & 0 & 0 & 0 & -I & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \tag{55a} ∂δx∂f(x⊞δx,u,0) δx=0 00000000I00000000U23F0000000−GRI00000000−I000000U26F0000000000000000000000 (55a)

其中：

U 23 F = − G R I ⌊ a m − b a ⌋ U^{F}_{23} = - {}^{G}R_I \lfloor a_m - b_a \rfloor U23F=−GRI⌊am−ba⌋
U 26 F = − ⌊ G g ⌋ B ( G g ) U^{F}_{26} = - \lfloor {}^{G}g \rfloor B({}^{G}g) U26F=−⌊Gg⌋B(Gg)
B ( ⋅ ) B(\cdot) B(⋅) 定义于公式 (13)

2. 对噪声的偏导

∂ f ( x , u , w ) ∂ w ∣ w = 0 [ − G R I 0 0 0 0 − G R I 0 0 0 0 I 0 0 0 0 I − I 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] (55b) \frac{\partial f(x, u, w)}{\partial w}\bigg|_{w=0} \begin{bmatrix} -{}^{G}R_I & 0 & 0 & 0 \\ 0 & -{}^{G}R_I & 0 & 0 \\ 0 & 0 & I & 0 \\ 0 & 0 & 0 & I \\ -I & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}\tag{55b} ∂w∂f(x,u,w) w=0 −GRI000−I0000−GRI00000000I00000000I0000 (55b)

对测量模型的偏导数

1. 对状态的偏导

∂ ( h ( x ⊞ δ x , 0 ) − h ( x , 0 ) ) ∂ δ x ∣ δ x = 0 = [ ⋮ G i 0 U i 3 H 0 0 0 U i 7 H G i , G R I ⋮ ] (56a) \frac{\partial \big( h(x \boxplus \delta x, 0) - h(x, 0) \big)}{\partial \delta x}\bigg|{\delta x=0}=\\ \begin{bmatrix} \vdots \\ G_i & 0 & U^{H}{i3} & 0 & 0 & 0 & U^{H}_{i7} & G_i, {}^{G}R_I \\ \vdots \end{bmatrix}\tag{56a} ∂δx∂(h(x⊞δx,0)−h(x,0)) δx=0= ⋮Gi⋮0Ui3H000Ui7HGi,GRI (56a)

其中：

U i 3 H = − G i G R I ⌊ I T L , L p i f ⌋ U^{H}_{i3} = - G_i{}^{G}R_I \lfloor {}^{I}T_L, {}^{L}p^f_i \rfloor Ui3H=−GiGRI⌊ITL,Lpif⌋
U i 7 H = − G i G R I I R L ⌊ L p i f ⌋ U^{H}_{i7} = - G_i {}^{G}R_I {}^{I}R_L \lfloor {}^{L}p^f_i \rfloor Ui7H=−GiGRIIRL⌊Lpif⌋

2. 对测量噪声的偏导

∂ ( h ( x , v ) − h ( x , 0 ) ) ∂ v ∣ v = 0 = diag ⁡ ( ⋯ , − G i G R I I R L , ⋯ ) (56b) \frac{\partial (h(x, v) - h(x, 0))}{\partial v}\bigg|_{v=0}= \operatorname{diag}(\cdots,\ - G_i {}^{G}R_I {}^{I}R_L,\ \cdots)\tag{56b} ∂v∂(h(x,v)−h(x,0)) v=0=diag(⋯, −GiGRIIRL, ⋯)(56b)

总结

将规范系统表示式（公式 54）以及偏导数（公式 55、56）提供给 IKFoM 工具包，即可构建一个紧耦合的激光雷达--惯性导航系统。

C. 实验结果

我们在三种不同场景下验证了由我们工具包实现的紧耦合激光雷达--惯导导航系统，即室内 UAV 飞行、室内快速摇动实验以及室外随机行走实验。它们分别记为 V1、V2 和 V3 。对于每个场景，我们在两组数据上进行测试，一组是我们自行采集的数据，另一组来自原论文 [15]。六个数据集分别记为 V1-01、V1-02、V2-01、V2-02、V3-01 和 V3-02 。在所有实验中，迭代卡尔曼滤波器（见 Algorithm 1）的最大迭代次数设置为 N max ⁡ = 4 N_{\max}=4 Nmax=4。

1) 室内 UAV 飞行

对于 UAV 飞行实验，我们只展示本工作采集的数据（即 V1-01 ）。实验在室内环境中进行（见 Fig. 10 (A)），UAV 从地面起飞后沿着圆形路径飞行。在路径跟随过程中，UAV 始终朝向安全网后的杂乱办公室区域（Fig. 10 (B)）。路径飞行完成后，人工接管 UAV 进行降落，使降落位置尽量与起飞点重合。

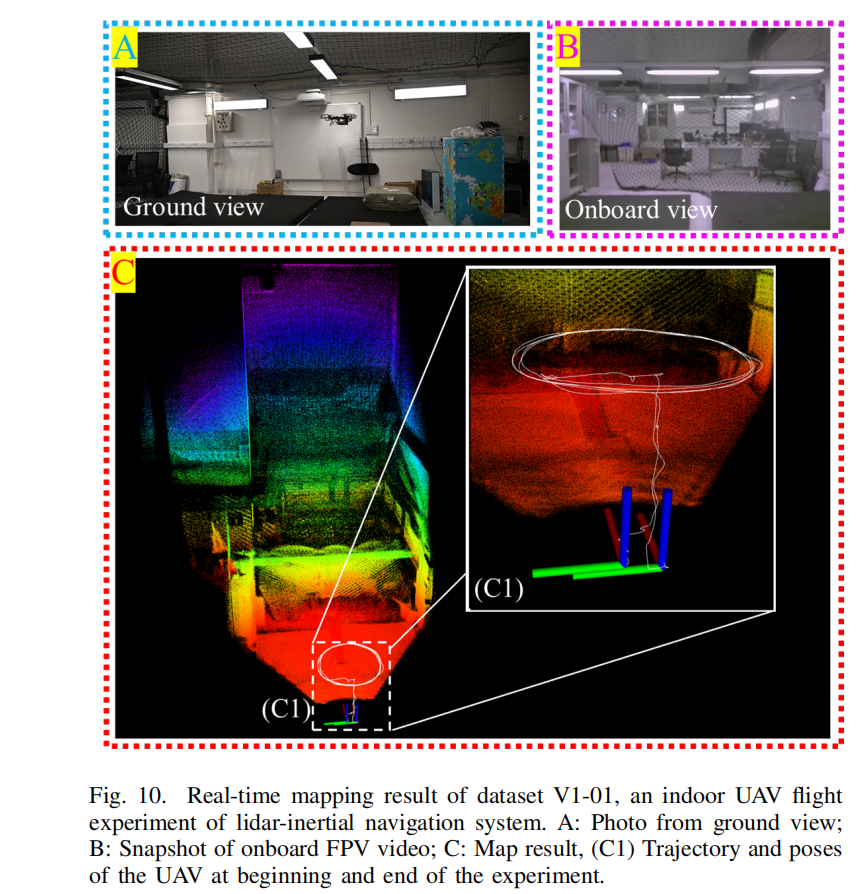
Fig. 10 © 展示了实时建图结果叠加系统估计的 3D 轨迹。可见本系统在杂乱室内环境中仍然能够实现一致的建图。位置漂移小于 0.9692% （即 22.81m 路径上的 0.2211m 漂移，见 Fig. 10 (C1)）。该漂移部分来自里程计误差的累积（SLAM 系统中常见），部分来自不准确的手动降落。

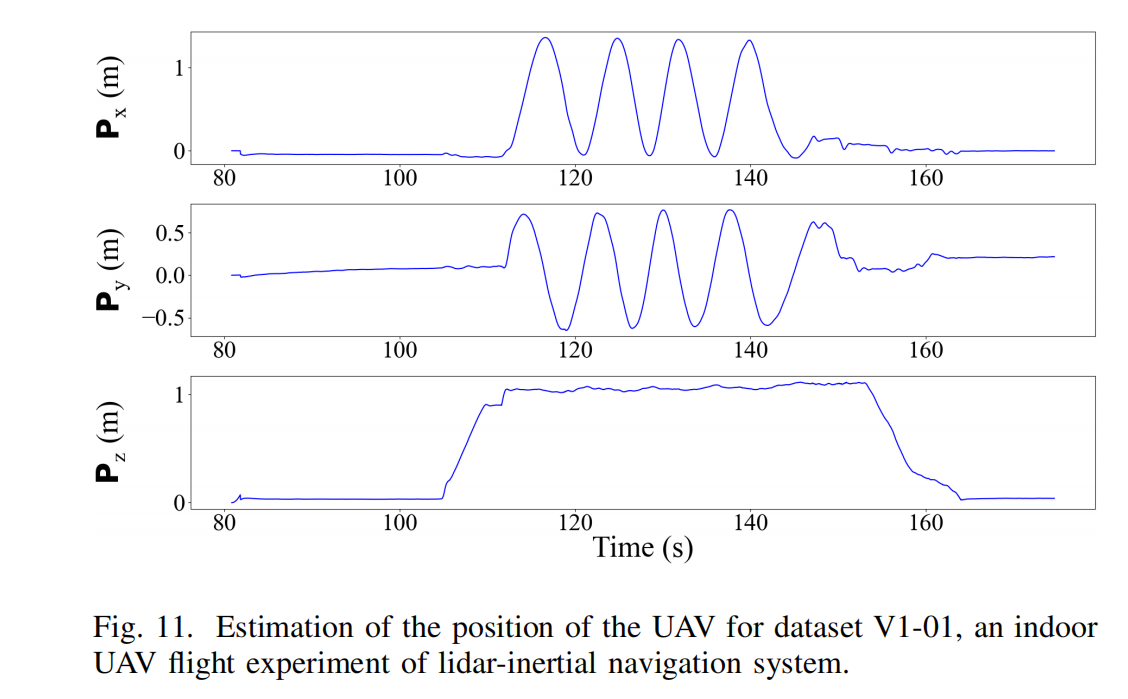
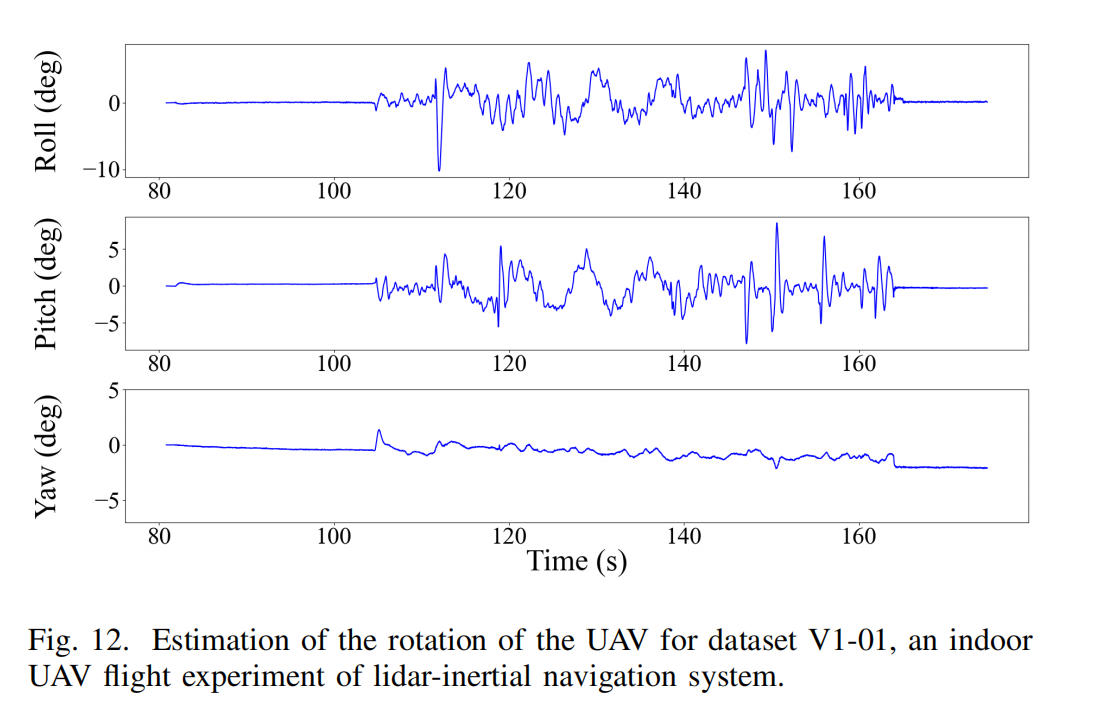
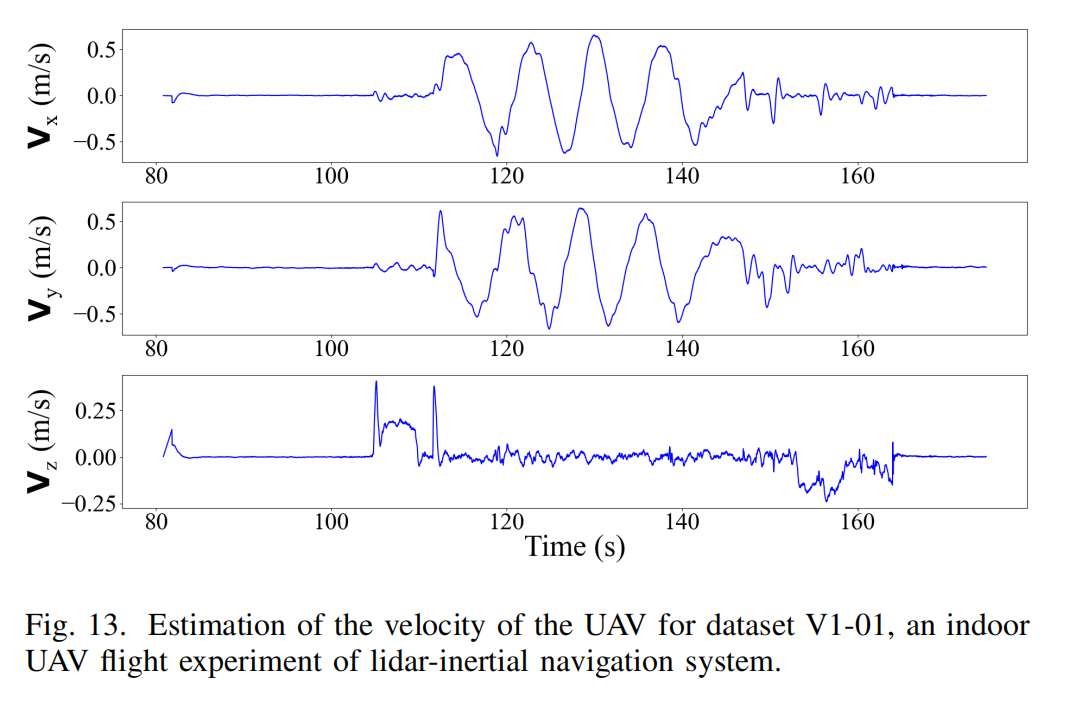
Fig. 11、Fig. 12 和 Fig. 13 分别展示了位置 G p I Gp_I GpI、旋转 G R I GR_I GRI 和速度 G v I Gv_I GvI 的估计轨迹，实验时间范围为 80.8393s 至 174.6590s。本系统实现了平滑的状态估计，适用于机载反馈控制，所有估计的状态变量都与实际运动良好一致。

数据集 V1-02 的表现相似（位置漂移为 0.6872%），由于篇幅限制未展示。更多实验演示可参考视频：
https://youtu.be/sz_ZlDkl6fA

2) 室内快速摇动

第二组实验在杂乱办公室环境中进行（Fig. 14 (A)）。实验中，搭载激光雷达与机载电脑的 UAV 由手持方式快速摇动（Fig. 14 (B)），最大旋转速度达到 356.85 deg/s （见 Fig. 14 (A) 的 FPV 图像与 Fig. 15 的 IMU 原始测量）。UAV 最终返回起始位置，使得可以计算里程计漂移。

Fig. 14 © 展示了数据集 V2-01 的实时建图结果。可见本系统即使在快速旋转情况下也能实现一致建图，这种场景往往会导致视觉--惯性里程计因图像失焦或运动模糊而表现不佳（见 Fig. 14 (A4)、(A5)）。如 Fig. 14 (C3) 所示，UAV 的最终估计位置与起点重合，位置漂移小于 0.1113% （110.64m 路径上的 0.1232m 漂移）。

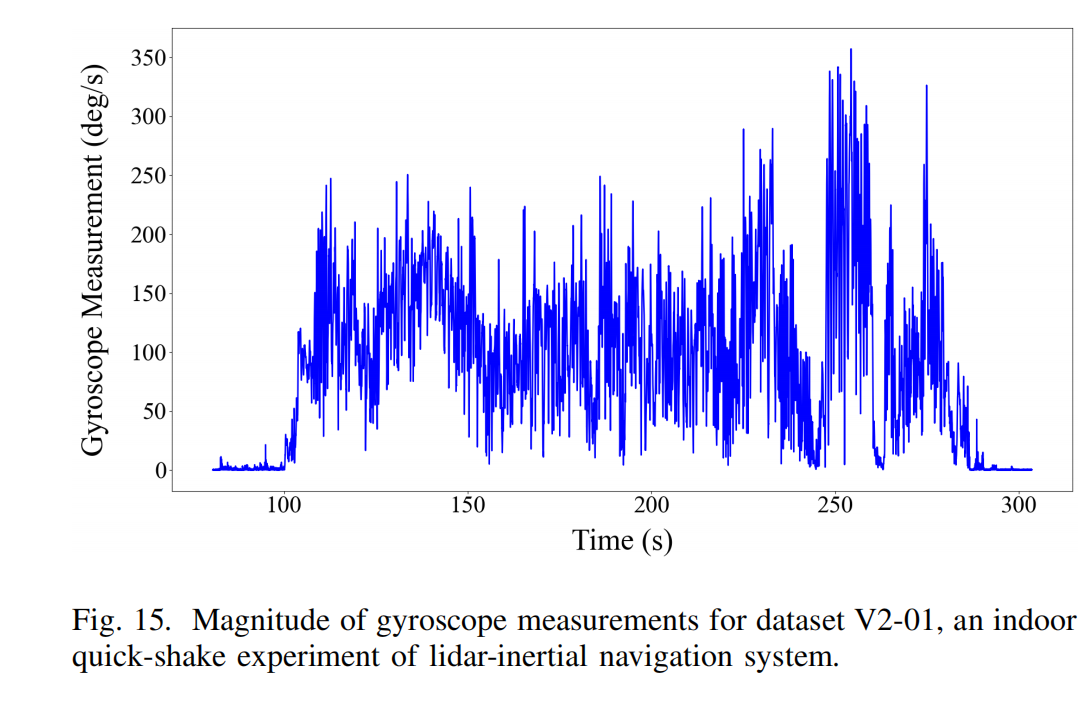
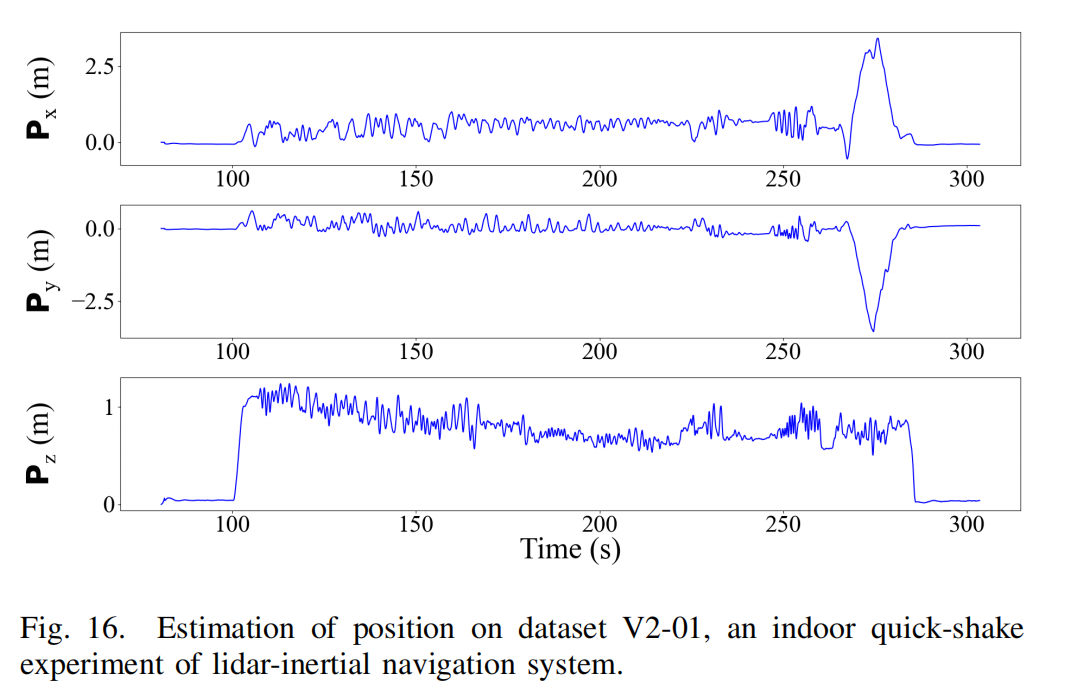
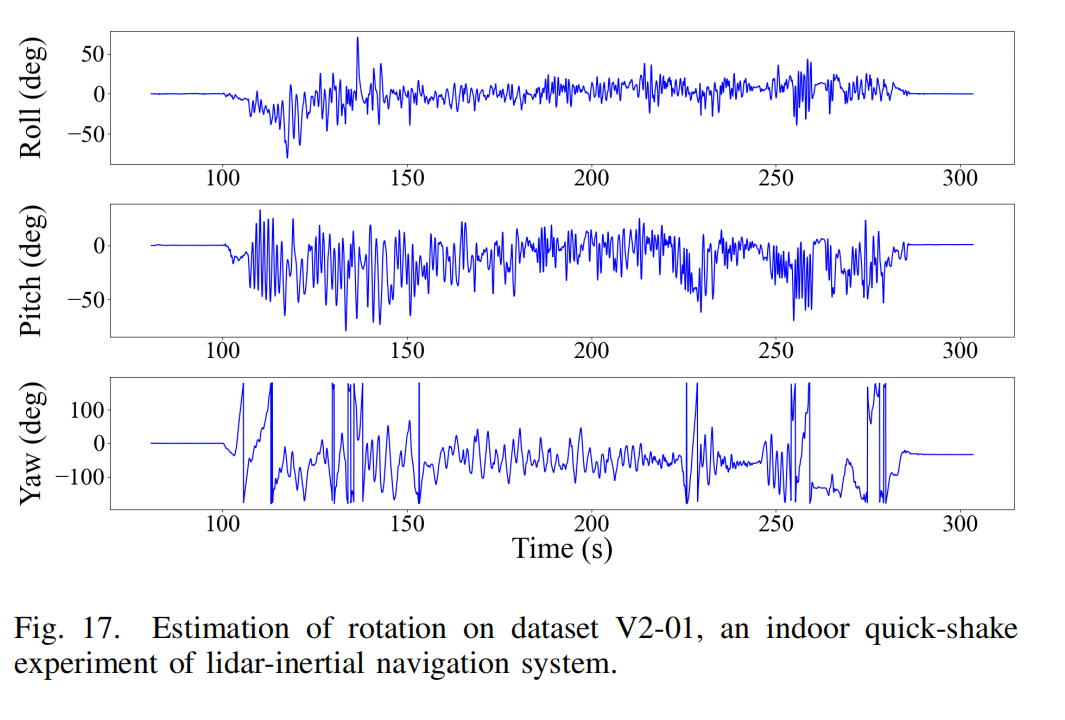
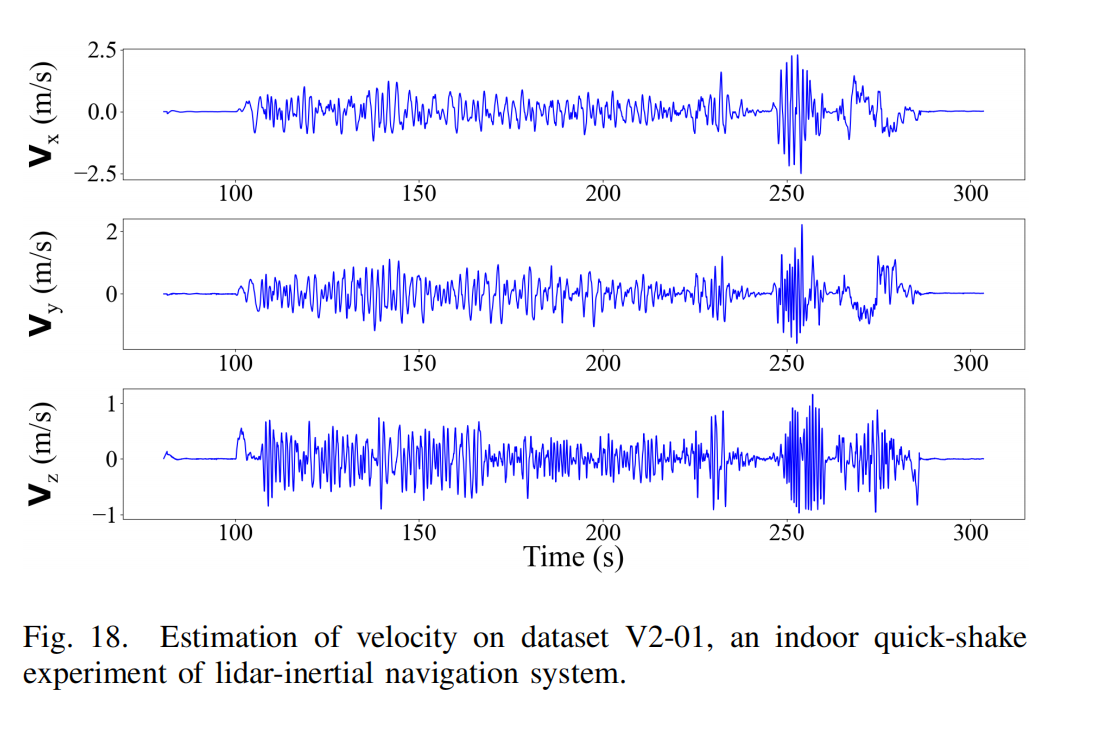
Fig. 16、Fig. 17 和 Fig. 18 展示了位置 G p I Gp_I GpI、旋转欧拉角 G R I GR_I GRI 与速度 G v I Gv_I GvI 的估计，实验时间为 80.5993s 至 303.499s。估计值呈现高频变化，与 UAV 的实际快速运动一致。约在 275s 的明显平移来自 UAV 的实际运动。更多视频演示参见：
https://youtu.be/sz_ZlDkl6fA

3) 室外随机行走

第三组实验在结构化的室外环境中进行，该环境是位于坡道与香港大学 Hawking Wong 大楼之间的走廊。在实验中，UAV 被手持沿道路移动并返回起点（Fig. 19 (A)）。

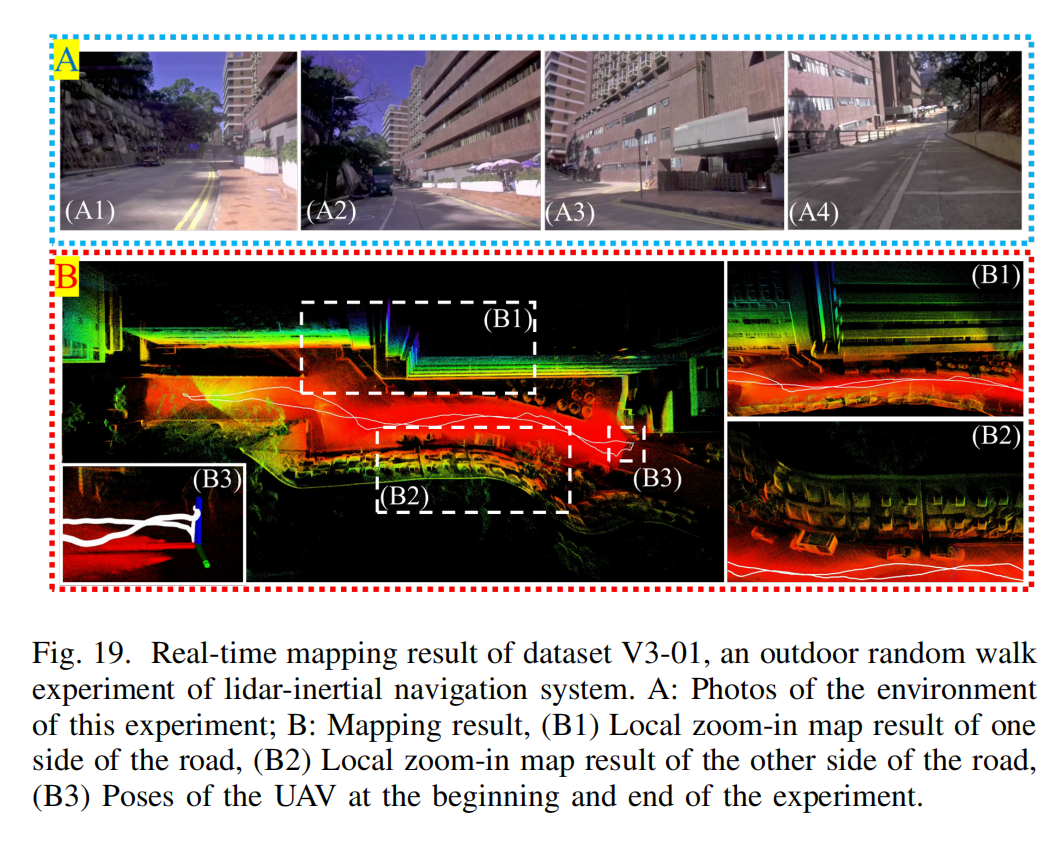
数据集 V3-01 的实时建图结果见 Fig. 19 (B)，清晰展示了建筑物、坡道上的车辆与砖体。位置漂移小于 0.0003538% （205.22m 路径上的 0.0007260m 漂移，见 Fig. 19 (B3)）。尽管该漂移极小，看似展示了系统的高精度，但不能直接视为真实误差，因为实际的手工落点无法如此精确。

更具参考价值的数据集 V3-02 得到 0.1575% 的位置漂移。其他结果与 V3-01 相似，因此未展示。

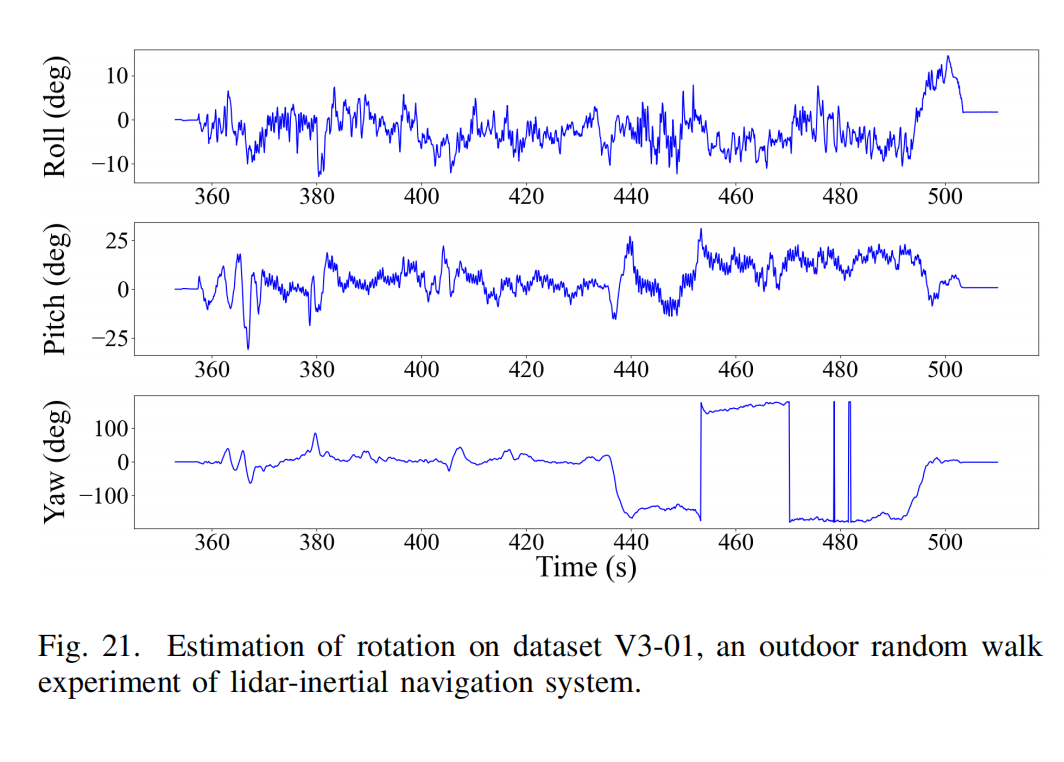
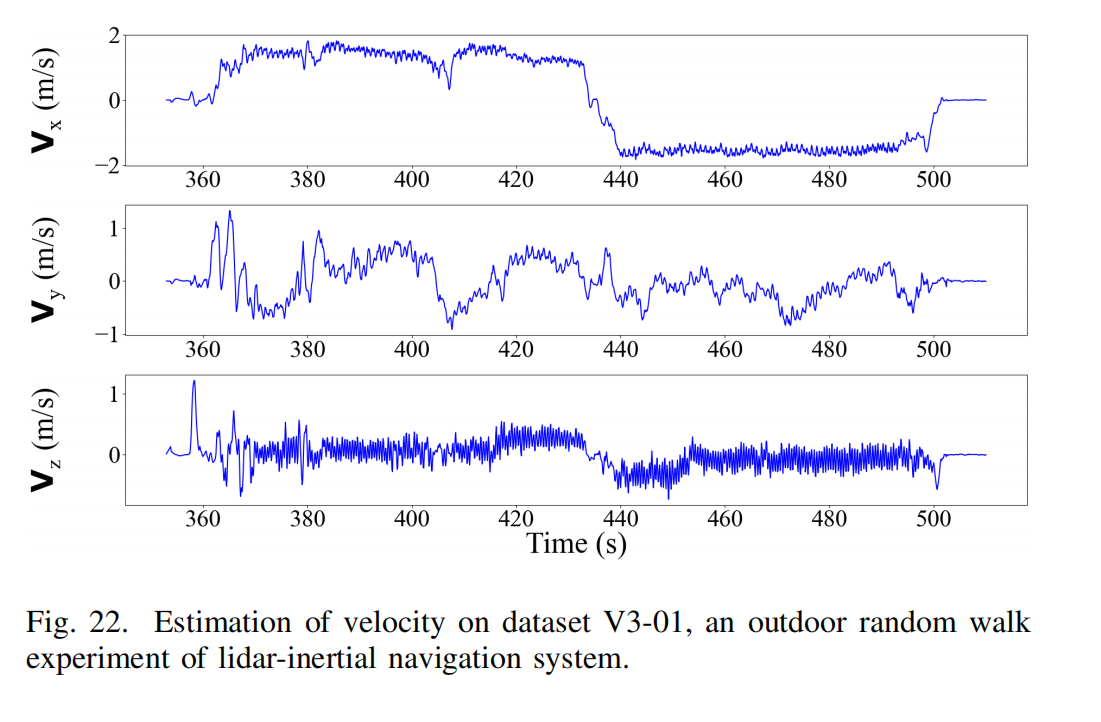
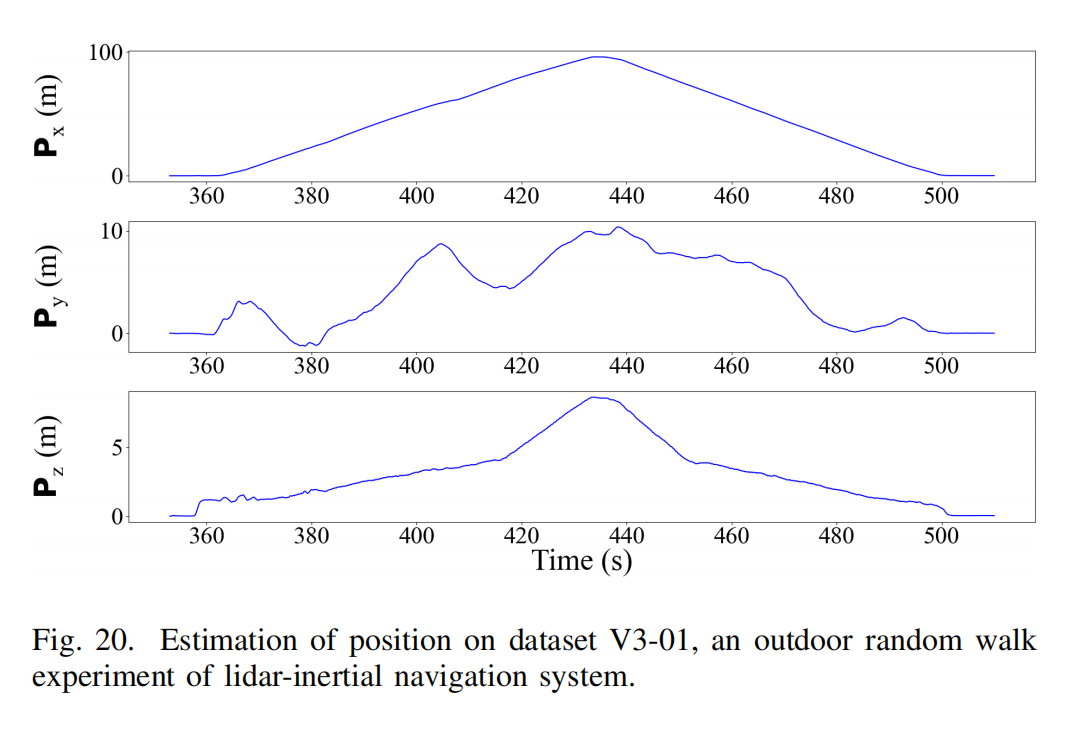
Fig. 20、Fig. 21 与 Fig. 22 展示了运动学参数估计，时间范围为 353.000s 至 509.999s。轨迹在 X 与 Z 方向上近似以中点时间对称，符合传感器沿同一路径前后移动的实际运动。

更多视频讨论参见：
https://youtu.be/sz_ZlDkl6fA

4) 在线估计外参、重力与 IMU 偏置

为了验证开发方法是一个正确工作的滤波器，在线标定参数（包括全球框架下的重力、IMU 偏置以及激光雷达--IMU 外参）必须收敛。此外，相同传感器配置下的外参估计应该在不同数据集间保持一致。因此，我们在多个数据集上评估外参的收敛值。

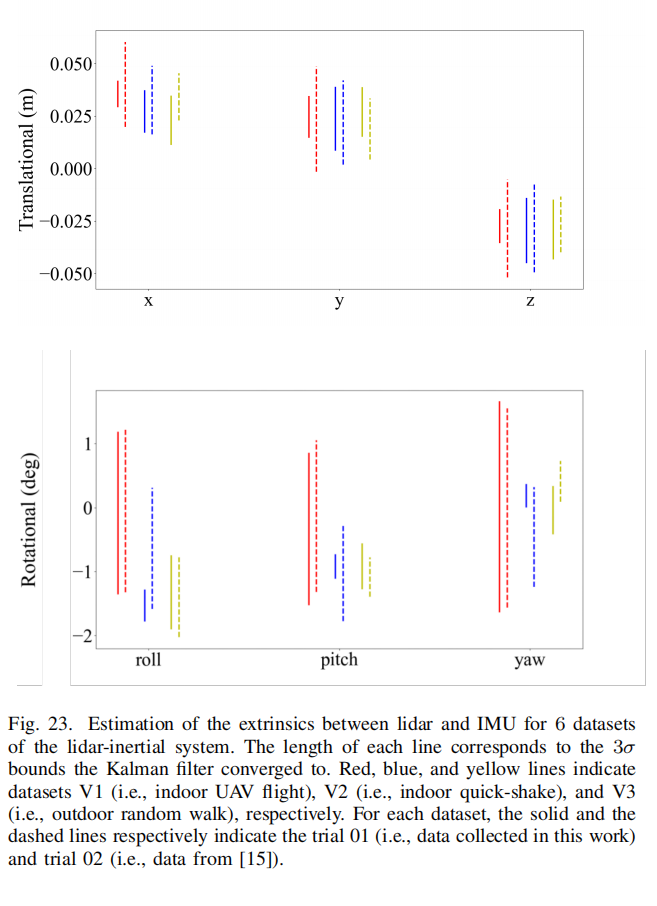
Fig. 23 展示了运行本工具包在全部六个数据集上的外参最终估计（旋转与平移）。外参初值来自制造商说明书。图中可见，不同数据集间的外参估计高度一致。平移的不确定性为 1--2 cm ，旋转的不确定性小于 1 ∘ 1^\circ 1∘。

其中，数据集 V1 的旋转外参方差明显大于其他数据集。这是因为飞行实验中 UAV 运动缓慢平滑，对参数估计的激励不足。手持实验 V2 与 V3 具有更大的激励，因此方差更小。此外，UAV飞行中电机旋转导致 IMU 噪声增大，也是可能原因。

此外，V2-02 的方差大于 V2-01（Fig. 23 的蓝线所示），这是因为 V2-01 具有 222.85s 的持续激励，而 V2-02 仅运行了 48.001s，滤波器尚未完全收敛（见 Fig. 24）。

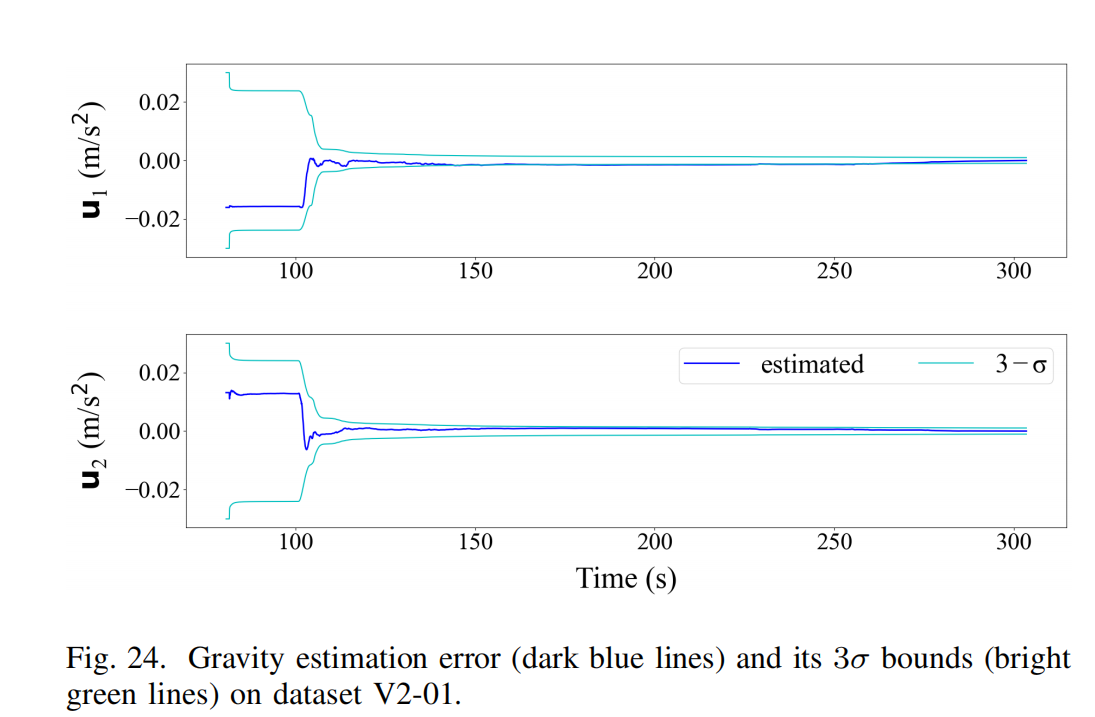
我们进一步检查重力估计的收敛情况。由于篇幅限制，仅展示数据集 V2-01 的结果。Fig. 24 展示了重力估计误差
u = G g ˉ ⊟ G g b k ∈ R 2 u = {}^G\bar{g} \boxminus {}^Gg_b^k \in \mathbb{R}^2 u=Ggˉ⊟Ggbk∈R2

其中 G g ˉ {}^G\bar{g} Ggˉ 为真实重力向量（使用最终收敛的估计代替）， G g b k {}^Gg_b^k Ggbk 为第 k k k 步估计。Fig. 24 同时展示了 Kalman 滤波器估计的 3 σ 3\sigma 3σ 区间。可以看到误差始终位于 3 σ 3\sigma 3σ 范围内，表明滤波器具有一致性。

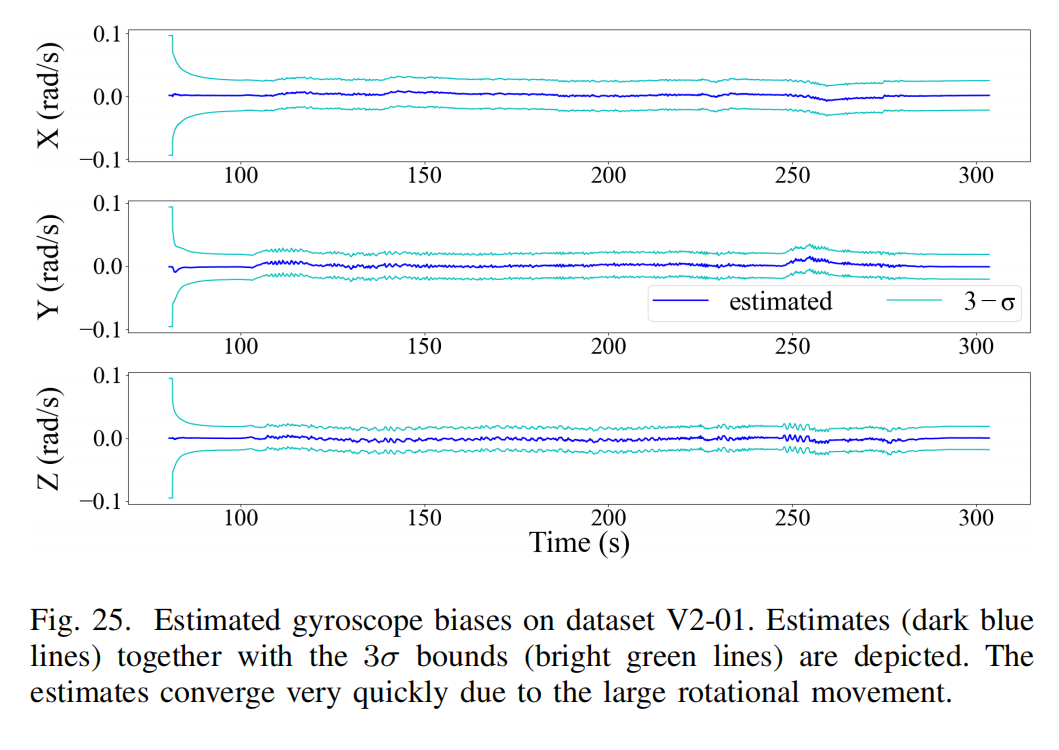
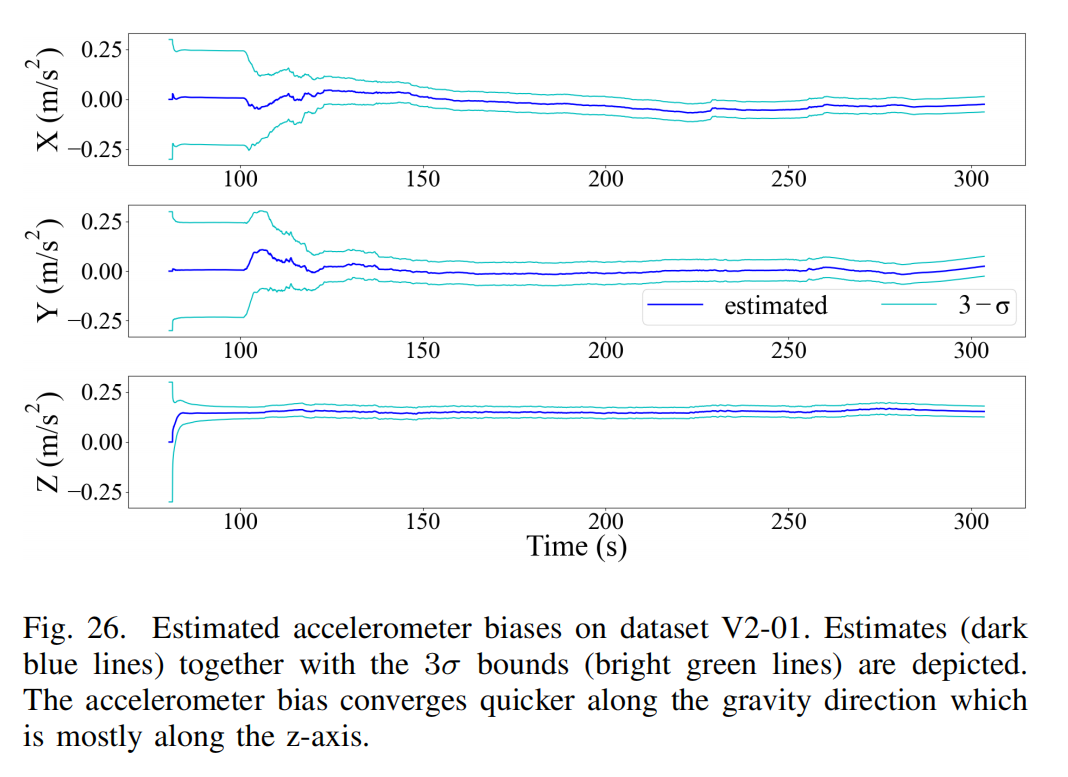
最后，我们检查 IMU 偏置估计的收敛情况（数据集 V2-01）。Fig. 25 与 Fig. 26 分别展示了偏置的估计过程与其 3 σ 3\sigma 3σ 区间。特别地，由于存在大幅旋转运动，陀螺仪偏置收敛很快；加速度计偏置在具有充分激励的条件下也能收敛，并且通常在重力方向（因实验开始时有大幅垂直运动）收敛更快（见 Fig. 14）。

5) 运行时间

为了进一步评估工具包的实用性，我们测量了其在三组数据集 V1-02、V2-02 与 V3-02 上的运行时间，并与 [15] 的实现进行比较。需要注意，[15] 也采用了迭代卡尔曼滤波器，但具有两点不同：

$15\] 中的迭代卡尔曼滤波器是 **人工推导** 的，其所需矩阵（如式 (35) 的 F x τ F_x\^\\tau Fxτ、 F w τ F_w\^\\tau Fwτ）直接编码，并精心利用了矩阵稀疏性以提高效率；而我们的实现直接使用工具包，将流形相关部分和系统相关部分分离。$

除此之外，其他实现均相同。两种实现均在 UAV 机载电脑（Fig. 9）上测试。

运行时间比较见 表 III ，该表展示了完成一步 Kalman 滤波（传播 + 更新）的平均时间。如预期，基于工具包的实现由于状态维度更高以及工具包开销更大而耗时更久。但该额外时间仍然可接受，两种实现均能实时运行。

VIII. 结论（CONCLUSION）

本文提出了一种机器人系统的规范化表示方法，并在此基础上构建了符号化的误差状态迭代卡尔曼滤波器（error-state iterated Kalman filter）。该规范化表示利用**流形（manifolds）**来表达系统状态，并通过运算符 ⊟ \boxminus ⊟ （差分）与 ⊞ \boxplus ⊞（加法更新）来描述系统模型。

基于机器人系统的这一规范化表示，我们在卡尔曼滤波框架下展示了 流形特定描述（manifold-specific descriptions） 与 系统特定描述（system-specific descriptions） 之间的分离原则（separation principle）。这种分离使得我们可以将流形结构模块化地封装进卡尔曼滤波器中，并进一步通过开发 C++ 工具包，使卡尔曼滤波器能够快速部署到任意运行在流形上的机器人系统中。

我们提出的方法及所开发的工具包已在三个不同场景下的紧耦合激光雷达--惯性导航系统中进行了验证。

附录

A. SO(3) 的偏微分

引理 1. 若 x , y ∈ S O ( 3 ) x, y \in \mathrm{SO}(3) x,y∈SO(3)， u , v ∈ R 3 u, v \in \mathbb{R}^3 u,v∈R3，则
∂ ( ( x ⊞ u ) ⊕ v ⊟ y ) ∂ u = A ( ( x ⊞ u ) ⊕ v ⊟ y ) − T E x p ( − v ) A ( u ) T \frac{\partial \big((x \boxplus u)\oplus v \mathbin{\boxminus} y\big)}{\partial u} = A\left((x \boxplus u)\oplus v \mathbin{\boxminus}y\right)^{-T} \mathrm{Exp}(-v) A(u)^T ∂u∂((x⊞u)⊕v⊟y)=A((x⊞u)⊕v⊟y)−TExp(−v)A(u)T

其中运算符 ⊞ \boxplus ⊞、 ⊟ \boxminus ⊟ 与 ⊕ \oplus ⊕ 的定义见式 (6)， A ( ⋅ ) A(\cdot) A(⋅) 的定义见式 (7)。

证明.

令
w = ( x ⊞ u ) ⊕ v ⊟ y w = (x \boxplus u)\oplus v \mathbin{\boxminus} y w=(x⊞u)⊕v⊟y

则有
E x p ( w ) = y − 1 x E x p ( u ) E x p ( v ) \mathrm{Exp}(w) = y^{-1} x \mathrm{Exp}(u)\mathrm{Exp}(v) Exp(w)=y−1xExp(u)Exp(v)

因此，当 u u u 发生一个小扰动 Δ u \Delta u Δu 时， w w w 将产生对应的小扰动 Δ w \Delta w Δw，满足：

E x p ( w + Δ w ) = y − 1 . x . E x p ( u + Δ u ) E x p ( v ) (57) \mathrm{Exp}(w+\Delta w) = y^{-1}.x .\mathrm{Exp}(u+\Delta u) \mathrm{Exp}(v) \tag{57} Exp(w+Δw)=y−1.x.Exp(u+Δu)Exp(v)(57)

利用文献 [33] 中的结论：

E x p ( u + Δ u ) = E x p ( u ) ( I + ⌊ A ( u ) T Δ u ⌉ ) \mathrm{Exp}(u+\Delta u) = \mathrm{Exp}(u)\Big(I + \big\lfloor A(u)^T \Delta u \big\rceil\Big) Exp(u+Δu)=Exp(u)(I+⌊A(u)TΔu⌉)

式 (57) 左侧可写为：

E x p ( w + Δ w ) = E x p ( w ) ( I + ⌊ A ( w ) T Δ w ⌉ ) \mathrm{Exp}(w+\Delta w) = \mathrm{Exp}(w)\Big(I + \big\lfloor A(w)^T \Delta w \big\rceil\Big) Exp(w+Δw)=Exp(w)(I+⌊A(w)TΔw⌉)

式 (57) 右侧可写为：

y − 1 . x . E x p ( u + Δ u ) E x p ( v ) = y − 1 x . E x p ( u ) ( I + ⌊ A ( u ) T Δ u ⌉ ) E x p ( v ) = E x p ( w ) E x p ( − v ) ( I + ⌊ A ( u ) T Δ u ⌉ ) E x p ( v ) \begin{aligned} y^{-1}. x .\mathrm{Exp}(u+\Delta u)\mathrm{Exp}(v) &\\= y^{-1} x.\mathrm{Exp}(u) \Big(I + \big\lfloor A(u)^T \Delta u \big\rceil\Big) \mathrm{Exp}(v) \ &\\= \mathrm{Exp}(w) \mathrm{Exp}(-v) \Big(I + \big\lfloor A(u)^T \Delta u \big\rceil\Big) \mathrm{Exp}(v) \end{aligned} y−1.x.Exp(u+Δu)Exp(v)=y−1x.Exp(u)(I+⌊A(u)TΔu⌉)Exp(v) =Exp(w)Exp(−v)(I+⌊A(u)TΔu⌉)Exp(v)

将式 (57) 两侧相等关系对比可得：

A ( w ) T Δ w = E x p ( − v ) A ( u ) T Δ u A(w)^T \Delta w = \mathrm{Exp}(-v) A(u)^T \Delta u A(w)TΔw=Exp(−v)A(u)TΔu

因此：

∂ ( ( x ⊞ u ) ⊕ v ⊟ y ) ∂ u = Δ w Δ u = A ( w ) − T E x p ( − v ) A ( u ) T \frac{\partial \big((x \boxplus u)\oplus v \mathbin{\boxminus} y\big)}{\partial u}= \frac{\Delta w}{\Delta u} = A(w)^{-T} \mathrm{Exp}(-v) A(u)^T ∂u∂((x⊞u)⊕v⊟y)=ΔuΔw=A(w)−TExp(−v)A(u)T

B. 复合流形（compound manifolds）的偏微分

引理 2. 若 x 1 , y 1 ∈ S 1 x_1, y_1 \in S_1 x1,y1∈S1； x 2 , y 2 ∈ S 2 x_2, y_2 \in S_2 x2,y2∈S2； u 1 , v 1 ∈ R n 1 u_1, v_1 \in \mathbb{R}^{n_1} u1,v1∈Rn1 且 u 2 , v 2 ∈ R n 2 u_2, v_2 \in \mathbb{R}^{n_2} u2,v2∈Rn2；其中 n 1 , n 2 n_1, n_2 n1,n2 分别是 S 1 , S 2 S_1, S_2 S1,S2 的维度。

定义复合流形 S = S 1 × S 2 S = S_1 \times S_2 S=S1×S2，其元素为
x = [ x 1 x 2 ] ∈ S , y = [ y 1 y 2 ] ∈ S , x = \begin{bmatrix} x_1 \ x_2 \end{bmatrix} \in S,\qquad y = \begin{bmatrix} y_1 \ y_2 \end{bmatrix} \in S, x=[x1 x2]∈S,y=[y1 y2]∈S,

向量
u = [ u 1 u 2 ] ∈ R n 1 + n 2 , v = [ v 1 v 2 ] ∈ R l 1 + l 2 , u = \begin{bmatrix} u_1 \ u_2 \end{bmatrix} \in \mathbb{R}^{n_1+n_2}, \qquad v = \begin{bmatrix} v_1 \ v_2 \end{bmatrix} \in \mathbb{R}^{l_1 + l_2}, u=[u1 u2]∈Rn1+n2,v=[v1 v2]∈Rl1+l2,

其中当 S 1 S_1 S1 是李群时 l 1 = n 1 l_1=n_1 l1=n1，当 S 2 S_2 S2 是李群时 l 2 = n 2 l_2=n_2 l2=n2。则有：

∂ ( ( ( x ⊞ s u ) ⊕ s v ) ⊟ s y ) ∂ u = [ ∂ ( ( ( x 1 ⊞ S 1 u 1 ) ⊕ s 1 v 1 ) ⊟ s 1 y 1 ) ∂ u 1 0 0 ∂ ( ( ( x 2 ⊞ S 2 u 2 ) ⊕ S 2 v 2 ) ⊟ s 2 y 2 ) ∂ u 2 ] \frac{\partial\big(((x \boxplus _su)\oplus _s v )\mathbin{\boxminus _s}y\big)}{\partial u}=\\ \begin{bmatrix} \displaystyle \frac{\partial\big(((x_1 \mathbin{\boxplus _{S_1}}u_1)\oplus{s_1 v_1) }\mathbin{\boxminus{s_1}} y_1\big)}{\partial u_1} & 0 \\ 0 & \displaystyle \frac{\partial\big(((x_2 \mathbin{\boxplus {S_2}}u_2)\oplus{S_2 v_2 })\mathbin{\boxminus{s_2}} y_2\big)}{\partial u_2} \end{bmatrix} ∂u∂(((x⊞su)⊕sv)⊟sy)= ∂u1∂(((x1⊞S1u1)⊕s1v1)⊟s1y1)00∂u2∂(((x2⊞S2u2)⊕S2v2)⊟s2y2)

证明

定义：

w = ( ( x ⊞ S u ) ⊕ S v ) ⊟ s y w = ((x \mathbin{\boxplus _S} u)\oplus_S v) \mathbin{\boxminus s}y w=((x⊞Su)⊕Sv)⊟sy

根据式 (14) 中 , ⊞ , ⊕ , ⊟ , ,\boxplus, \oplus, \boxminus, ,⊞,⊕,⊟, 的复合运算规则，

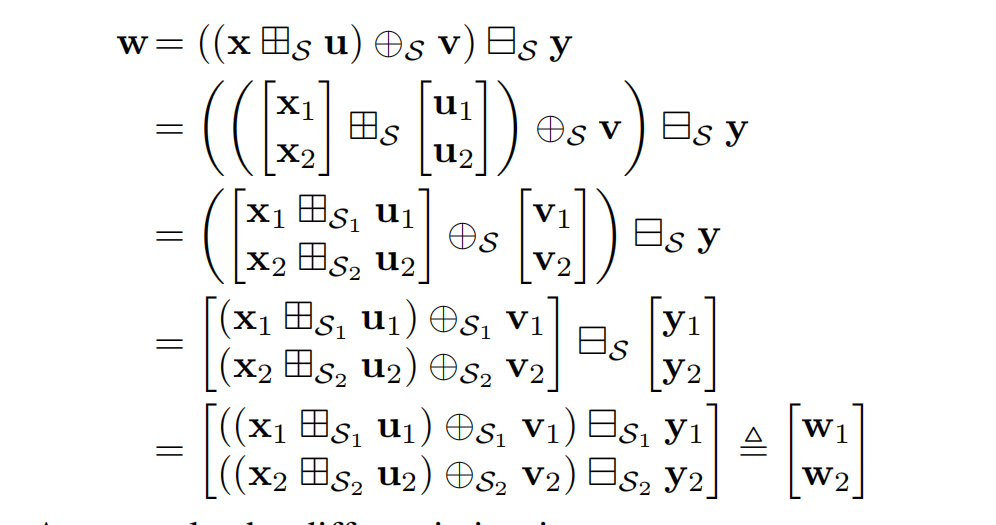
因此，其导数矩阵为：

∂ w ∂ u = [ ∂ w 1 ∂ u 1 ∂ w 1 ∂ u 2 ∂ w 2 ∂ u 1 ∂ w 2 ∂ u 2 ] = [ ∂ w 1 ∂ u 1 0 0 ∂ w 2 ∂ u 2 ] \frac{\partial w}{\partial u}= \begin{bmatrix} \displaystyle \frac{\partial w_1}{\partial u_1} & \displaystyle \frac{\partial w_1}{\partial u_2} \\ \displaystyle \frac{\partial w_2}{\partial u_1} & \displaystyle \frac{\partial w_2}{\partial u_2} \end{bmatrix}= \begin{bmatrix} \displaystyle \frac{\partial w_1}{\partial u_1} & 0 \\ 0 & \displaystyle \frac{\partial w_2}{\partial u_2} \end{bmatrix} ∂u∂w= ∂u1∂w1∂u1∂w2∂u2∂w1∂u2∂w2 = ∂u1∂w100∂u2∂w2

考虑 w 1 w_1 w1 与 w 2 w_2 w2 的结构，可得：

∂ ( ( ( x 1 ⊞ S 1 u 1 ) ⊕ s 1 v 1 ) ⊟ s 1 y 1 ) ∂ u 1 0 0 ∂ ( ( ( x 2 ⊞ S 2 u 2 ) ⊕ S 2 v 2 ) ⊟ s 2 y 2 ) ∂ u 2 \] \\begin{bmatrix} \\displaystyle \\frac{\\partial\\big(((x_1 \\mathbin{\\boxplus _{S_1}}u_1)\\oplus{s_1 v_1) }\\mathbin{\\boxminus{s_1}} y_1\\big)}{\\partial u_1} \& 0 \\\\ 0 \& \\displaystyle \\frac{\\partial\\big(((x_2 \\mathbin{\\boxplus _{S_2}}u_2)\\oplus_{S_2 v_2 })\\mathbin{\\boxminus{s_2}} y_2\\big)}{\\partial u_2} \\end{bmatrix} ∂u1∂(((x1⊞S1u1)⊕s1v1)⊟s1y1)00∂u2∂(((x2⊞S2u2)⊕S2v2)⊟s2y2) 证毕。 *** ** * ** *** 下节相关内容：[A Quick Guide for the Iterated Extended Kalman Filter on Manifolds]()