链式存储范式下的二叉树：基础操作实现解析

前言
二叉树是数据结构中的基础核心结构，其操作覆盖创建、遍历、属性统计、结构判断等关键场景。本文围绕二叉树的手动创建、四种遍历方式（前 / 中 / 后序 + 层序）、节点数 / 高度等属性接口、完全二叉树判断等核心操作展开解析，结合代码实现拆解每类操作的逻辑思路，帮助快速掌握二叉树的基础操作体系。

📚 初阶数据结构

【时间复杂度+空间复杂度】

【顺序表】

[☆ 前序遍历](#☆ 前序遍历)

[☆ 中序遍历](#☆ 中序遍历)

[☆ 后序遍历](#☆ 后序遍历)

[☆ 层序遍历](#☆ 层序遍历)

[▷ 二叉树遍历选择题](#▷ 二叉树遍历选择题)

1、二叉树的简易创建（手动方式）

首先定义二叉树节点的结构：

cpp 复制代码

typedef int BTDataType;
typedef struct BinaryTreeNode
{
    BTDataType _data;                  // 节点存储的数据
    struct BinaryTreeNode* _left;      // 指向左孩子的指针
    struct BinaryTreeNode* _right;     // 指向右孩子的指针
}BTNode;

接着通过手动方式快速创建二叉树（需配合BuyNode函数来创建单个节点）：

cpp 复制代码

BTNode* BuyNode(BTDataType data)
{
    // 1. 申请节点内存
    BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
    // 2. 校验内存申请是否成功（避免空指针访问）
    assert(newNode != NULL);  // 也可根据需求改为返回NULL，搭配上层判断
    
    // 3. 初始化节点
    newNode->_data = data;    // 赋值节点数据
    newNode->_left = NULL;    // 左孩子初始化为空
    newNode->_right = NULL;   // 右孩子初始化为空

    // 4. 返回新节点
    return newNode;
}

// 二叉树的手动创建
BTNode* CreatBinaryTree()
{
    // 先创建6个独立节点，分别存入数据1~6
    BTNode* node1 = BuyNode(1);
    BTNode* node2 = BuyNode(2);
    BTNode* node3 = BuyNode(3);
    BTNode* node4 = BuyNode(4);
    BTNode* node5 = BuyNode(5);
    BTNode* node6 = BuyNode(6);

    // 手动建立节点间的父子关系
    node1->_left = node2;   // 节点1的左孩子是节点2
    node1->_right = node4;  // 节点1的右孩子是节点4
    node2->_left = node3;   // 节点2的左孩子是节点3
    node4->_left = node5;   // 节点4的左孩子是节点5
    node4->_right = node6;  // 节点4的右孩子是节点6

    return node1;  // 返回根节点（节点1）
}

手动创建的树的形状：

cpp 复制代码

注意：以上代码只是为了快速进入二叉树操作学习的 "临时手动创建方式"，并非实际开发中创建二叉树的标准方法，真正的二叉树创建逻辑会在后续详细讲解。

2、二叉树的遍历

所谓二叉树遍历（Traversal），是指按照某种预设规则，依次对二叉树中的每个节点执行对应操作，且每个节点仅被操作一次。其中，"访问节点时具体做什么操作"，需根据实际应用场景来确定。

遍历不仅是二叉树中最重要的运算之一，更是实现二叉树其他操作的基础。

按照规则，二叉树的遍历包含前序、中序、后序三种递归结构遍历，核心区别是 "访问根节点的时机"：

1、前序遍历（Preorder Traversal，又称先序遍历）：访问根节点的操作，发生在遍历其左、右子树之前（对应 NLR：根→左子树→右子树）。

2、中序遍历（Inorder Traversal）：访问根节点的操作，发生在遍历其左、右子树的中间（对应 LNR：左子树→根→右子树）。

3、后序遍历（Postorder Traversal）：访问根节点的操作，发生在遍历其左、右子树之后（对应 LRN：左子树→右子树→根）。

由于遍历中被访问的节点一定是某棵子树的根，因此可以用N（根节点）、L（左子树）、R（右子树） 来简化描述：

前序遍历 = 先根遍历（NLR）
中序遍历 = 中根遍历（LNR）
后序遍历 = 后根遍历（LRN）

除上述三种递归结构遍历外，二叉树还支持层序遍历：设二叉树的根节点所在层数为 1，层序遍历的规则是：从根节点出发，先访问第 1 层的根节点，再从左到右访问第 2 层的所有节点，接着按同样方式访问第 3 层、第 4 层...... 以此类推，自上而下、自左至右逐层访问树中所有节点。

前中后序遍历演示：
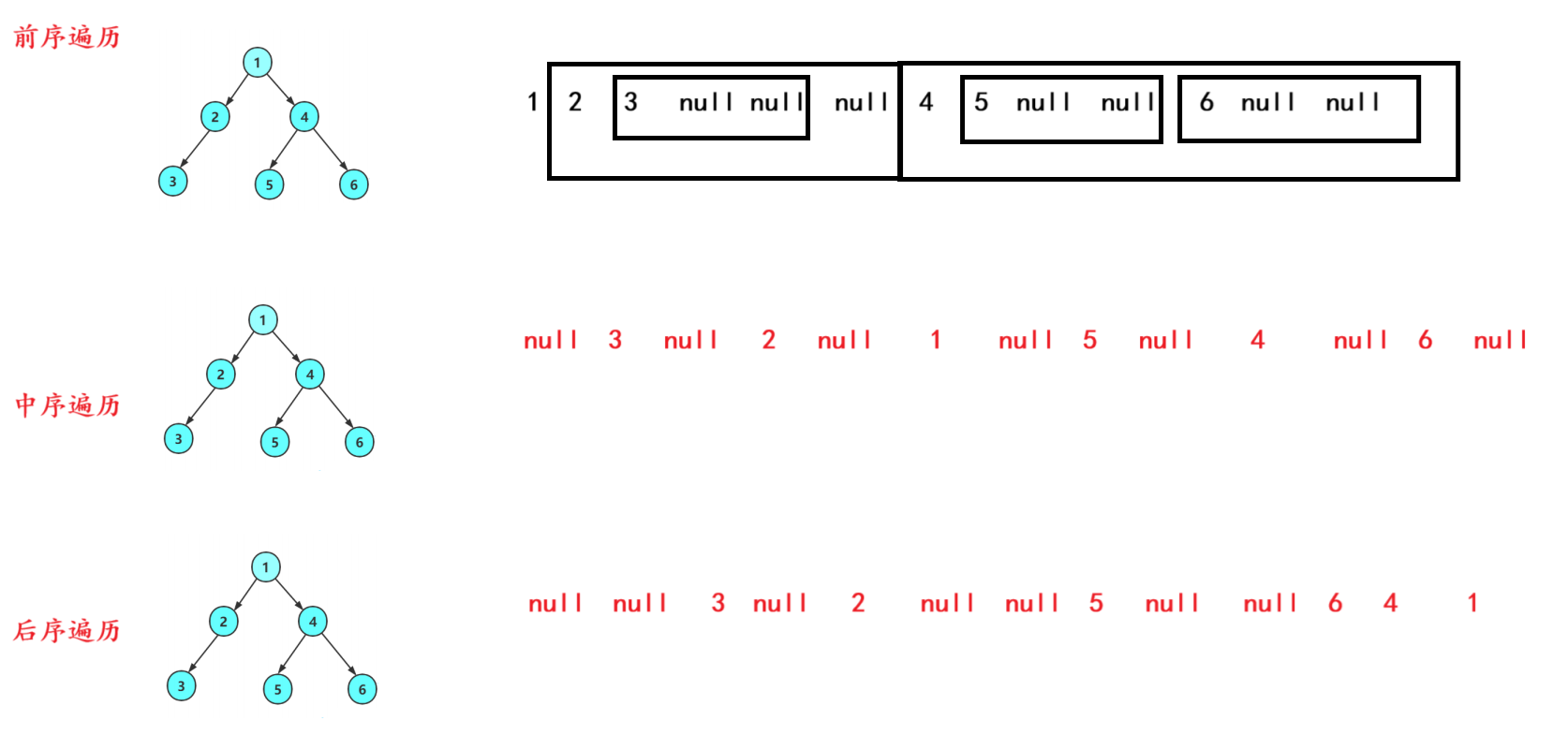前中后序遍历演示

1. 前序遍历（NLR：根→左子树→右子树）

结果： 1 2 3 null null null 4 5 null null 6 null null

2. 中序遍历（LNR：左子树→根→右子树）

结果： null 3 null 2 null 1 null 5 null 4 null 6 null

3. 后序遍历（LRN：左子树→右子树→根）

结果： null null 3 null 2 null null 5 null null 6 4 1

总结：

遍历结果的差异，本质是 "访问根节点的时机" 不同：

前序：见根就记，再处理左右；

中序：先挖到底找最左，记完左再记根，最后记右；

后序：把左右都处理完，最后才记根。而null的补充，是为了明确 "当前节点的左 / 右孩子不存在"，保证遍历序列能唯一还原二叉树结构。

☆ 前序遍历

cpp 复制代码

//前序遍历
void PreOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
    printf("%d ",root->val );
    PreOrder(root->left ); 
    PreOrder(root->right);
}

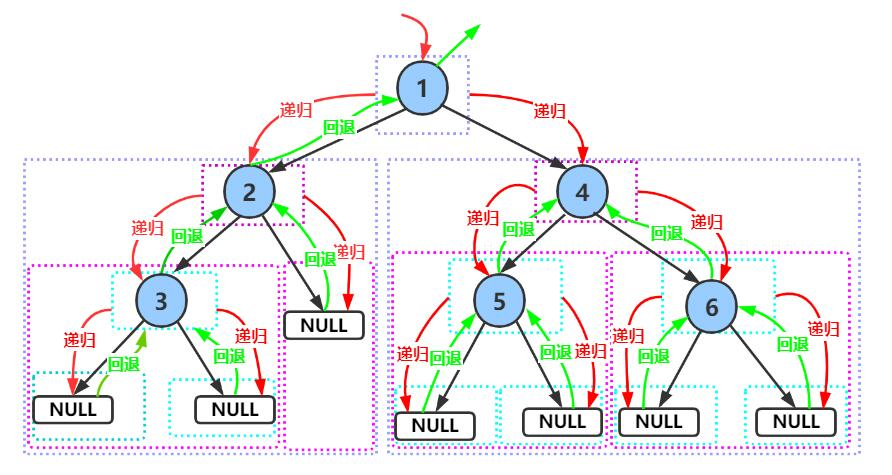前序遍历递归示意图

前序遍历递归流程示意说明

这个示意图直观展示了代码的递归执行过程（红色箭头代表 "递归进入"，绿色箭头代表 "递归返回"）：

1、从根节点1开始，先打印1，再递归进入左子树（节点2）；

2、到节点2后，先打印2，再递归进入左子树（节点3）；

3、到节点3后，先打印3，再递归进入其左孩子（空，打印NULL后返回），再递归进入其右孩子（空，打印NULL后返回）；

4、节点3处理完后返回节点2，递归进入其右孩子（空，打印NULL后返回）；

5、节点2处理完后返回节点1，递归进入右子树（节点4）；

6、后续对节点4、5、6的处理逻辑与上述一致，最终按 "根→左→右" 的顺序输出完整序列。

整个流程完全贴合代码中 "先打印根、再递归左、最后递归右" 的前序规则，递归的 "进入 - 返回" 过程也清晰体现了遍历的深度优先特性。

☆ 中序遍历

这段代码实现了二叉树的中序遍历（左→根→右），核心逻辑与前序遍历一致，仅调整了 "访问根节点的时机"：

cpp 复制代码

//中序遍历
//左 根 右
void InOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }

    InOrder(root->left);
    printf("%d ", root->val);
    InOrder(root->right);

}

递归示意图我就不画了，和前序差不多，只不过访问根节点的时机发生了变化

其递归流程与前序遍历的 "进入 - 返回" 逻辑一致，区别仅在于：前序是 "先打根、再递归左右"，而中序是 "先递归左、再打根、最后递归右"。

以之前的二叉树（根 1，左 2 右 4；2 左 3；4 左 5 右 6）为例，中序遍历会先递归到最左的节点 3，打印3后返回节点 2，再打印2，之后继续按 "左→根→右" 的顺序输出，最终得到序列：NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL。

☆ 后序遍历

这段代码实现了二叉树的后序遍历（左→右→根），逻辑框架与前序、中序一致，核心差异是 "访问根节点的时机最晚"：

cpp 复制代码

// 二叉树后序遍历
//左 右 根
void PostOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }

    PostOrder(root->left );
    PostOrder(root->right );
    printf("%d ", root->val);

}

其递归的 "进入 - 返回" 流程和前序、中序一致，区别在于：必须等左、右子树都遍历完成后，才会访问当前根节点。

以之前的二叉树（根 1，左 2 右 4；2 左 3；4 左 5 右 6）为例，后序遍历会先递归到最左的节点 3，等其左、右子树（均为空）处理完后，才打印3；再返回节点 2，处理完其右子树（空）后打印2；后续按 "左→右→根" 的顺序，最终得到序列：NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1。

☆ 层序遍历

这段代码实现了二叉树的层序遍历（自上而下、自左至右逐层访问） ，核心是借助队列实现 "先入先出" 的访问顺序：

cpp 复制代码

void LevelOrder(BTNode* root)
{
    Queue q;
    QueueInit(&q);  // 初始化队列

    if (root)       // 若根节点非空，先入队
        QueuePush(&q, root);

    while (!QueueEmpty(&q))  // 队列非空时循环
    {
        BTNode* front = QueueFront(&q);  // 取队头节点
        QueuePop(&q);                    // 队头节点出队
        printf("%d ", front->val);       // 访问（打印）当前节点

        // 若左孩子非空，入队
        if (front->left)
            QueuePush(&q, front->left);
        // 若右孩子非空，入队
        if (front->right)
            QueuePush(&q, front->right);
    }

    QueueDestroy(&q);  // 销毁队列，释放资源
}

逻辑流程（以之前的二叉树为例）：

1、初始化队列，将根节点1入队；

2、队头1出队，打印1 → 把1的左孩子2、右孩子4入队；

3、队头2出队，打印2 → 把2的左孩子3入队；

4、队头4出队，打印4 → 把4的左孩子5、右孩子6入队；

5、队头3出队，打印3 → 无孩子，不处理；

6、队头5出队，打印5 → 无孩子，不处理；

7、队头6出队，打印6 → 无孩子，不处理；

8、队列空，循环结束。

最终输出序列为1 2 4 3 5 6，完美对应 "逐层、从左到右" 的层序遍历规则。

▷ 二叉树遍历选择题

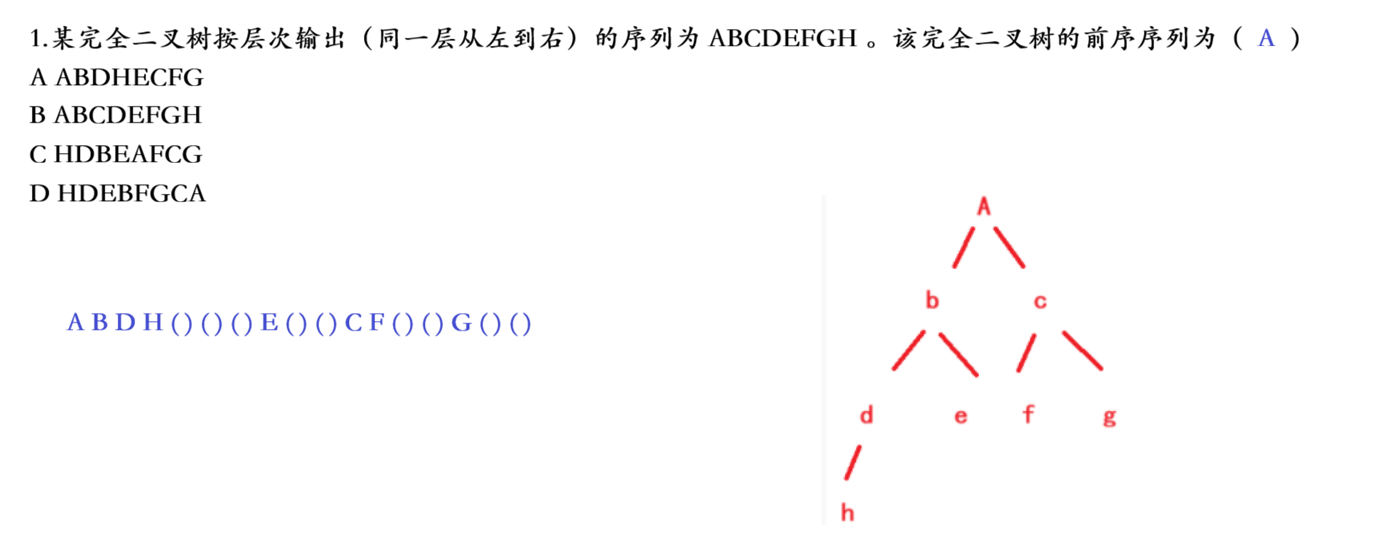
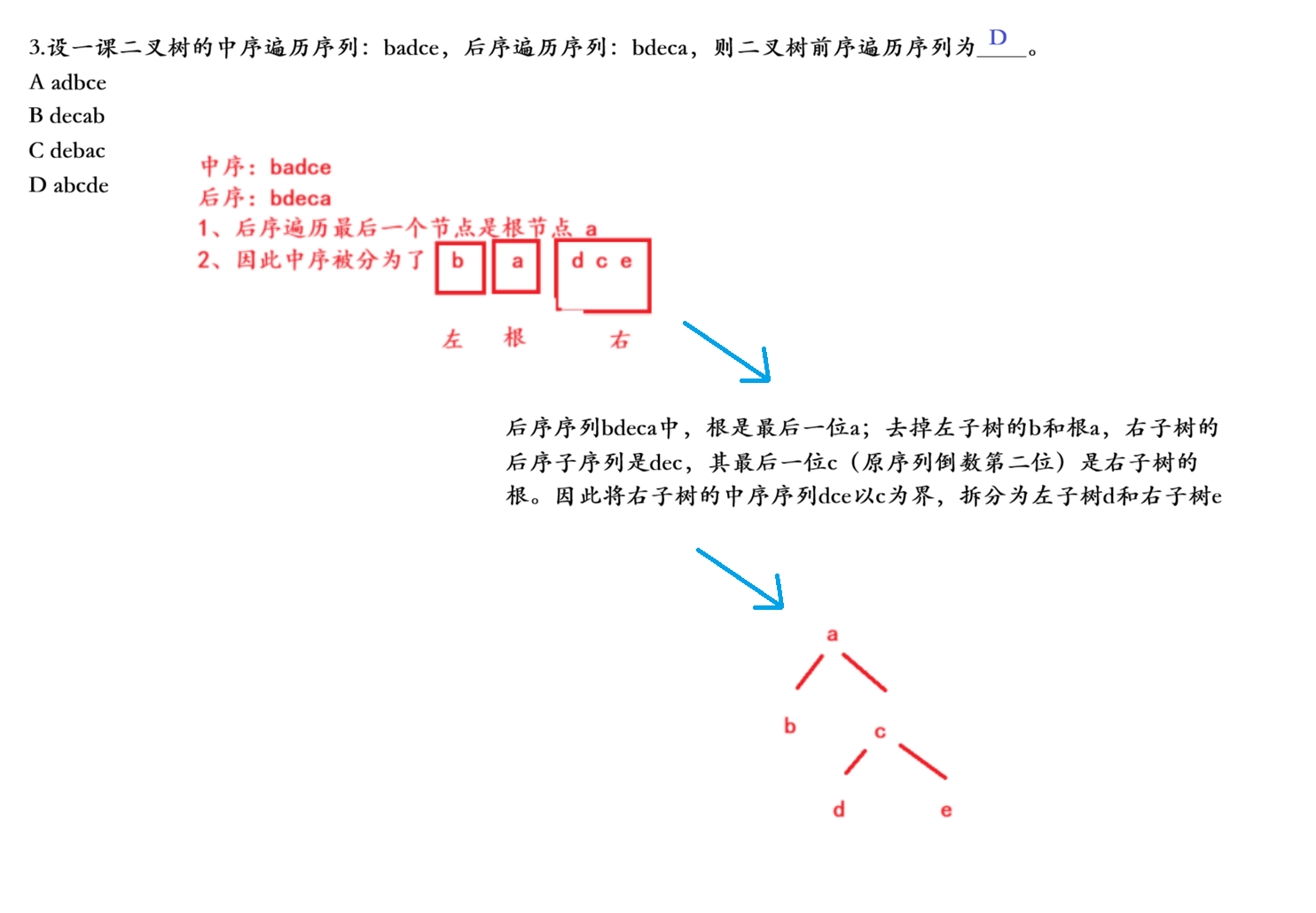
3、节点个数以及高度等接口

© 二叉树节点个数

方式 1：递归返回值法

cpp 复制代码

// 求二叉树节点个数，即"当前节点 + 左子树节点数 + 右子树节点数"
int BinaryTreeSize(BTNode* root)
{
    if (root == NULL)  // 空节点贡献0个节点
    {
        return 0;
    }
    // 1（当前节点） + 左子树节点数 + 右子树节点数
    return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

逻辑说明：通过递归 "分治"，把问题拆分为 "当前节点 + 左子树 + 右子树" 的节点数之和；空节点返回 0，非空节点返回 1 加左右子树的结果，最终得到总节点数

优点：无全局变量，调用后直接获取结果，逻辑简洁

方式 2：全局变量累加法

cpp 复制代码

int size = 0;  // 全局变量，用于累计节点数

// 通过"非空节点则size+1"的方式，遍历所有节点；遇到空节点直接返回
void TreeSize(BTNode* root)
{
    if (root == NULL)
    {
        return ;
    }
    size++;  // 访问到非空节点，计数+1
    TreeSize(root->left);  // 遍历左子树
    TreeSize(root->right); // 遍历右子树
}

逻辑说明 ：借助全局变量size，遍历二叉树的每个节点：遇到非空节点则size+1，最终size的值就是总节点数。

缺点：多次调用前需要手动重置size为 0，否则会累计之前的结果

© 二叉树叶子节点个数

cpp 复制代码

// 求左右子树叶节点的和
// 结束条件：节点为空，或左右子树均为空（即叶子节点）
int BinaryTreeLeafSize(BTNode* root)
{
    if (root == NULL)  // 空节点，无叶子节点
    {
        return 0;
    }
    // 左右子树都为空 → 当前是叶子节点，贡献1个
    if (root->left == NULL && root->right == NULL)
    {
        return 1;
    }
    // 总叶子数 = 左子树叶节点数 + 右子树叶节点数
    return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

逻辑说明：

空节点返回 0；

左右子树都空的节点是叶子，返回 1；

非叶子节点的叶子数，等于其左右子树的叶子数之和

© 二叉树第k层节点个数

cpp 复制代码

// 求第k层节点数 = 左子树第k-1层节点数 + 右子树第k-1层节点数
// 当k==1时，当前节点就是第k层节点；遇到空节点返回0
int BinaryTreeLevelKSize(BTNode* root, int k)
{
    if (root == NULL)  // 空节点，第k层无节点
    {
        return 0;
    }
    if (k == 1)  // k=1时，当前节点就是第1层节点，贡献1个
    {
        return 1;
    }
    // 第k层节点数 = 左子树第k-1层节点数 + 右子树第k-1层节点数
    return BinaryTreeLevelKSize(root->left, k - 1) 
         + BinaryTreeLevelKSize(root->right, k - 1);
}

逻辑说明：

空节点返回 0；

k=1时，当前节点就是目标层，返回 1；

非k=1时，递归求左右子树的第k-1层节点数之和，即当前树的第k层节点数

© 二叉树查找值为x的节点

cpp 复制代码

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
    if (root == NULL)  // 空节点，无匹配值
    {
        return NULL;
    }


    if (root->val == x)  // 当前节点值等于x，返回该节点
    {
        return root;
    }


    // 先在左子树查找，找到则直接返回结果
    BTNode* leftFind = BinaryTreeFind(root->left, x);
    if (leftFind)
    {
        return leftFind;
    }


    // 左子树没找到，再在右子树查找
    BTNode* rightFind = BinaryTreeFind(root->right, x);
    if (rightFind)
    {
        return rightFind;
    }

    // 不推荐写法
    // if (BinaryTreeFind(root->left, x))
    // {
    //     return BinaryTreeFind(root->left, x);
    // }
    // if (BinaryTreeFind(root->right, x))
    // {
    //     return BinaryTreeFind(root->right, x);
    // }
    // 问题：判断和返回时会重复递归查找同一子树，时间效率从O(n)降至O(2ⁿ)


    // 左右子树都没找到，返回NULL
    return NULL;
}

逻辑说明：

空节点返回NULL；

当前节点值匹配x，直接返回该节点；

先递归查左子树，找到则返回；左子树没找到，再递归查右子树；

左右子树都无匹配，最终返回NULL

© 二叉树的高度

cpp 复制代码

// 树的高度 = 左右子树中更深的高度 + 1（当前节点的高度）
int BinaryTreeDepth(BTNode* root)
{
    if (NULL == root)  // 空节点高度为0
    {
        return 0;
    }
    // 递归求左、右子树的高度
    int LeftHight = BinaryTreeDepth(root->left);
    int RightHight = BinaryTreeDepth(root->right);
    // 返回"更深子树的高度 + 1"（+1是当前节点的贡献）
    return LeftHight > RightHight ? LeftHight + 1 : RightHight + 1;

    // 不推荐写法
    // return BinaryTreeDepth(root->left) > BinaryTreeDepth(root->right) ? BinaryTreeDepth(root->left) + 1 : BinaryTreeDepth(root->right) + 1;
    // 问题：同一子树的高度会被重复计算（判断和返回时各算一次），时间效率极低
}

逻辑说明：

空节点的高度为 0；

先递归计算左、右子树的高度；

树的高度是 "左右子树中较高的那个高度 + 1"（+1对应当前节点所在的）

cpp 复制代码

//判断二叉树是否为完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);


	//找队列第一个空
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//判断是不是空节点，不是的话就继续入左右子树的节点
		if (front == NULL)
		{
			break;
		}
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}

	//剩下的都是空的话就代表是完全二叉树
	//否则就不是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//有一个不为空就代表不是完全二叉树
		if (front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}

核心逻辑：

完全二叉树的特性是 "层序遍历到第一个空节点后，后续必须全为空节点"。这段代码通过层序遍历 + 队列检测实现判断：

先层序遍历所有节点，把每个节点的左右孩子（包括空节点）都入队；

遇到第一个空节点时停止入队；

检查队列剩余节点：若全为空 → 是完全二叉树；若有非空节点 → 不是完全二叉树。

4、二叉树的创建和销毁

☺二叉树的销毁

cpp 复制代码

// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{
	if (*root == NULL)
	{
		return;
	}
	BinaryTreeDestory(&((*root)->left));
	BinaryTreeDestory(&((*root)->right));

	free(*root);
	*root = NULL;
}

后序销毁原因：

✅ 先销毁左 / 右子树，再释放当前节点 → 避免先释放父节点导致子节点成野指针、内存泄漏；❌ 若先序 / 中序销毁，会丢失子节点访问路径，无法完整释放。

代码关键：

① 二级指针：修改外部根节点指针，最终置空；

② 递归终止：空节点直接返回，防崩溃；

③ 置空操作：释放内存后指针置 NULL，避免野指针访问。

☺二叉树的创建

cpp 复制代码

// 通过前序遍历的数组"ABD##E##H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(char* a, int* pi)
{
    // 1. 遇到'#'表示空节点，下标后移并返回NULL
    if (a[*pi] == '#')
    {
        (*pi)++;  // 下标推进，跳过当前'#'
        return NULL;
    }

    // 2. 创建当前节点，赋值并推进下标
    BTNode* root = (BTNode*)malloc(sizeof(BTNode));  // 为当前节点分配内存
    root->val = a[*pi];  // 取当前下标对应的字符作为节点值
    (*pi)++;  // 下标推进，准备处理下一个元素

    // 3. 递归创建左、右子树（前序遍历：根→左→右）
    root->left = BinaryTreeCreate(a, pi);  // 递归创建左子树
    root->right = BinaryTreeCreate(a, pi); // 递归创建右子树

    return root;  // 返回当前节点，作为父节点的左/右孩子
}

int main()
{
    char a[] = {"ABD##E##H##CF##G##"};  // 前序遍历序列（'#'表示空节点）
    int i = 0;  // 数组下标，记录当前读取到的位置
    BTNode* root = BinaryTreeCreate(a, &i);  // 传下标地址，保证递归中同步更新
    PreOrder(root);  // 前序遍历验证创建结果
    BinaryTreeDestory(&root);  // 销毁二叉树，避免内存泄漏
    return 0;
}

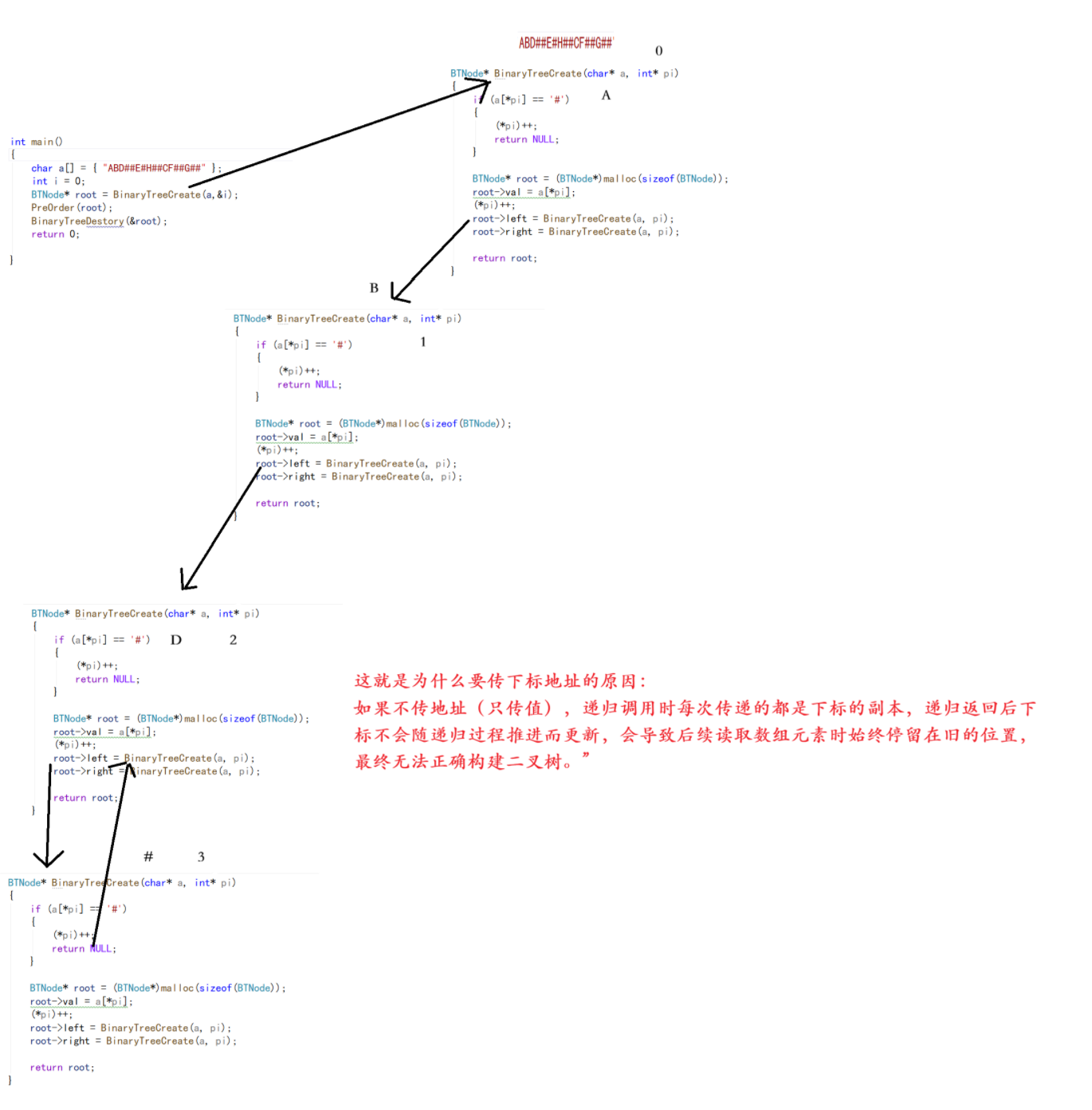
代码逻辑:

核心规则：按「根→左→右」前序遍历顺序构建二叉树；

空节点处理 ：遇到#返回 NULL，下标后移跳过#；

下标传地址 ：pi是地址，(*pi)++能让所有递归分支共享下标进度，避免重复读数组；

节点创建：先给当前节点分配内存、赋值，再递归建左 / 右子树；

收尾操作：遍历验证构建结果，销毁二叉树避免内存泄漏。

链式存储范式下的二叉树：基础操作实现解析

1、二叉树的简易创建（手动方式）

2、二叉树的遍历

☆ 前序遍历

☆ 中序遍历

☆ 后序遍历

☆ 层序遍历

▷ 二叉树遍历选择题

3、节点个数以及高度等接口

© 二叉树节点个数

© 二叉树叶子节点个数

© 二叉树第k层节点个数

© 二叉树查找值为x的节点

© 二叉树的高度

© 判断二叉树是否为完全二叉树

4、二叉树的创建和销毁

☺二叉树的销毁

☺二叉树的创建