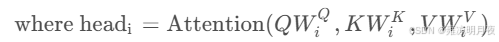深度学习网络笔记Ⅲ(注意力机制)

1.起源：

常见的网络结构包括FC/CNN/RNN，本章主要学习经RNN(循环神经网络)，Transformer架构，和其重点是完全基于注意力机制，完全摒弃了循环和卷积。究竟是什么样的原因和时代背景让工程师们选择完全摒弃循环和卷积，是为了解决什么样的问题？接下来就来进一步学习。

RNN结构

文献引入：Google团队发布的经典论文

Attention is All you Need

1.问题产生：Transformer的由来

基于2017年的时代背景下：

问题产生：

处理序列数据的主流方法是循环神经网络（RNN）及其变种。RNN的基本思想是按时间步骤逐个处理序列中的元素，每个时间步的输出不仅依赖于当前输入，还依赖于之前所有时间步的信息。但是普通的RNN存在梯度消失问题，难以学习长距离依赖关系。

应对方式：

研究者们开发了LSTM（长短期记忆网络）和GRU（门控循环单元）等改进版本。

LSTM：通过引入门控机制（输入门、遗忘门、输出门）来控制信息的流动，能够更好地保持长期记忆。

GRU：则是LSTM的简化版本，用更少的参数实现类似的效果。

编码器-解码器架构是处理序列到序列任务的标准框架，编码器将输入序列编码成固定长度的向量表示，解码器根据这个表示生成输出序列。

---

注意力机制的核心思想⭐

注意力机制的核心思想是让模型在生成每个输出时，都能够"回头看"整个输入序列，并根据相关性给不同位置的输入分配不同的权重。

传统的序列到序列模型主要依赖两种架构：循环神经网络（RNN）和卷积神经网络（CNN）。这些模型通常采用编码器-解码器框架，编码器负责理解输入序列，解码器负责生成输出序列。为了让编码器和解码器更好地协作，研究者们引入了注意力机制作为桥梁。发现注意力机制效果十分的好。作者们在这里提出了一个大胆的想法：既然注意力机制如此有效，为什么不完全基于注意力机制构建模型呢？

->

Transformer的核心思想------抛弃传统的循环和卷积结构，纯粹依靠注意力机制来处理序列数据。

优点：

1.并行化能力的大幅提升，因为不再需要按时间步骤顺序处理，可以同时处理序列中的所有位置。

2.训练效率的显著改善，大大减少了训练时间。

->

作者们还证明了Transformer的通用性，它不仅在机器翻译任务上表现出色，在其他自然语言处理任务如句法分析上也展现了强大的能力，这表明Transformer可能成为一个通用的序列建模架构。

Transformer的革命性：

无论两个位置相距多远，都只需要恒定数量的操作（实际上是一次矩阵乘法）就能建立直接联系。这种设计确实会带来一个副作用：由于注意力机制会对所有位置进行加权平均，可能会稀释重要信息的表示。 但作者们通过多头注意力机制巧妙地解决了这个问题，让模型能够同时关注不同类型的信息。

---

2.自注意力机制

**传统注意力机制：**通常用在编码器-解码器架构中，解码器在生成每个输出时会"注意"编码器的不同位置，这是跨序列的注意力。

自注意力机制：序列内部的注意力机制，它让序列中的每个位置都能够与同一序列中的所有其他位置建立直接联系。这种机制特别适合处理需要理解长距离依赖关系的任务。

小案例：

比如在处理句子"The cat sat on the mat"时，自注意力让"cat"这个词不仅能看到自己，还能直接看到"The"、"sat"、"on"、"the"、"mat"等所有其他词，并根据语义相关性给它们分配不同的权重。

特点：自注意力的强大之处在于它能够让模型自动学会关注最相关的信息，而不需要人工设计特征。

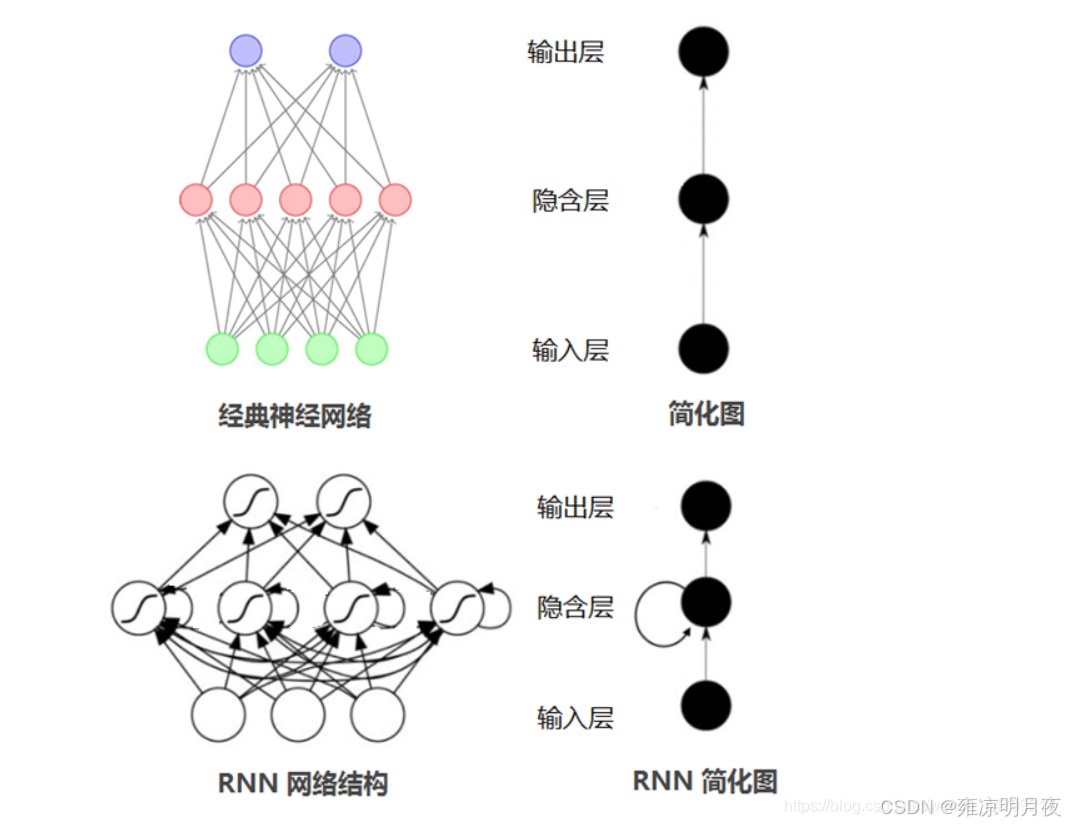
Transformer的模型架构（左：编码器，右：解码器）

---

2.注意力函数概述和理解

我们已经了解到Transformer模型基本构造和由来，接下来我们继续整理明白这个重点：注意力机制中的注意力函数究竟是什么？关于Attention的由来原论文中是这样表述的：

An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.

译文：

注意力函数可以描述为将查询和一组键值对映射到输出的过程，其中查询、键、值和输出都是向量。输出被计算为值的加权和，其中分配给每个值的权重由查询与相应键的兼容性函数计算得出。

注意力机制的本质是：

通俗理解：(与我query需求越相关的东西其权重越大，我将越可能做选择)

我想吃一种食物**（查询query），我们去餐厅吃饭，首先根据菜单上的食物类别（keys）,通过对比我的需求(query)和菜单的类别(keys)相关程度取决我要不要往下细看食物列表(values),最终会根据我的需求query与菜单上的类别keys的相关性程度进行加权组合->得到我最终的选择(output)。**

1.通过这种机制，模型能够动态地从大量候选信息中选择最相关的部分，并将它们有机地组合起来。

2.这种设计的优雅之处在于它完全是可微分的，可以通过反向传播进行端到端的训练，让模型自动学会如何进行有效的信息检索和聚合。

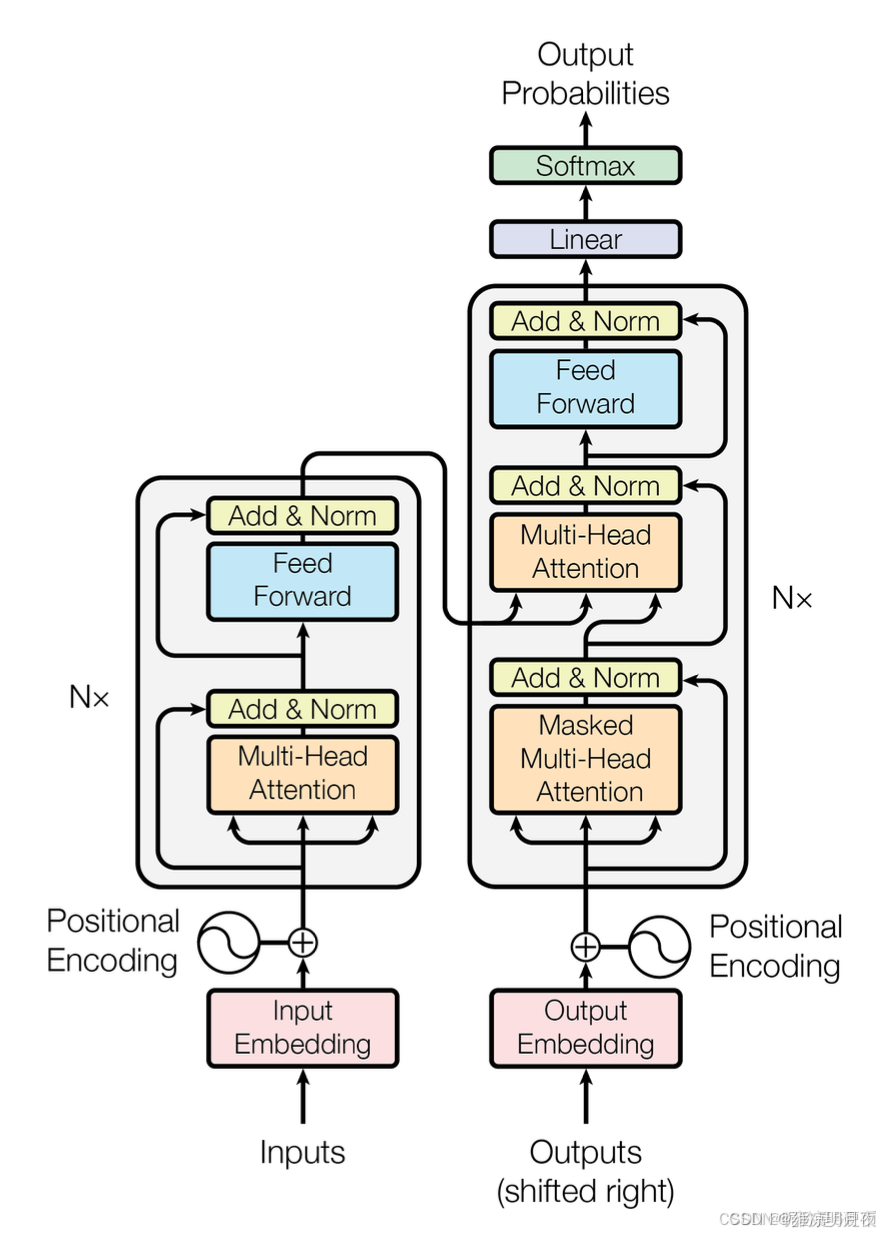
⭐我们将注意力机制数学公式化就将得到其公式为：

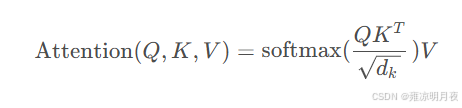
Q/K/V 都是同一组输入经过不同线性变换得到的向量 / 张量

• Q："查询" 向量（代表当前要计算注意力的对象）
• K："键" 向量（代表所有输入的特征标识）
• V："值" 向量（代表所有输入的实际内容）

• 比如在翻译任务中，输入句子的每个词会生成对应的 Q/K/V，Q 是当前词的查询，K/V 是所有词的键和值。
• Q是观察者产生的，K和V是被观察者产生的

⭐步骤理解

分子上的点集：计算 "查询 Q" 与 "所有键 K" 的相似度。

分母上的根号d：作用是缩放操作,避免梯度消失 。

用 softmax 得到的注意力权重，对所有 V 做加权求和，得到的是融合了 "关注重点" 的输出。

意义：

矩阵Q的每一行代表一个查询向量，K的每一行代表一个键向量，V的每一行代表一个值向量，Q*K的转置计算的是所有查询与所有键之间的相似度矩阵，其中第( i , j ) 个元素表示第i 个查询与第j个键的相似度。再进行缩放，对每一行应用softmax函数，得到是每个查询对所有键的注意力权重分布。最后乘以值矩阵V ，实现了加权求和的过程。

⭐⭐⭐

计算得到的是score，例如score = [16,4096,4096] = [N,Q,V]：

0轴上的16代表 批次*多头数量num_size。

1轴上的4096代表4096个观察者query。

2轴上的4096代表4096个观察者每个人观察4096个对象key。

接着就要进一步计算attention = score*V**(批次矩阵乘法)** ,此处的V代表的 N个Key 对应的 Value 特征。计算的前提是score 矩阵的最后一维K_num=4096必须等于 V 张量的倒数第二维V_num=4096。所以V必须是[16,4096,XXX],这个XXX代表的是「实体特征向量」。

当每个value实体有768个【实体特征向量】，则其计算为attention = score*V**=****[16,4096,4096]***[16,4096,768] = [16,4096,768]。

最终得到 4096 个 768 维的注意力增强特征

2.多头注意力

核心思想：

观察一个物体，我们应该让多个人分多个角度分析同一个物体。每个"头"都通过不同的线性变换矩阵将原始的查询、键、值投影到更低的维度空间中。每个头都能捕捉到数据中不同类型的模式和关系。学习到的特征提取过程。最后的线性投影将这个拼接后的表示转换回原始的模型维度，确保输出能够与网络的其他部分兼容。这种设计既保持了计算效率，又大大增强了模型的表达能力。

⭐多头注意力的一个关键优势：避免信息的平均化损失。

案例：

单头注意力：所有的信息都被融合到同一个表达空间， 这就像把所有颜色的颜料混合在一起

多头注意力：通过将表示空间分割成多个子空间，让每个子空间专门处理特定类型的信息。这样，不同类型的依赖关系和模式可以在各自的子空间中得到清晰的表达，而不会被其他类型的信息所干扰

通过学习不同的投影矩阵，每个头能够自动专门化处理不同类型的信息，这种自动的任务分工是多头注意力强大表达能力的根源。

---

3.注意力机制的代码实现

1.自注意力

核心思路：实现数学模型中的步骤

实现过程：

1.QKV的全连接初始化

2.softmax(Q*(K的转置)/缩放系数) = score的实现

3.score*V 加权求和得到结果

#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
@Project ：deep_learning
@File ：test.py
@IDE ：PyCharm
@Author ：wjj
@Date ：2025/12/28 21:45
@Description:
"""
import torch
from torch import nn
from torch.nn import functional as F

class SelfAttention(nn.Module):
    def __init__(self, in_dim=1024, qkv_dim=768):
        super(SelfAttention, self).__init__()
        self.w_q = nn.Linear(in_features=in_dim, out_features=qkv_dim)
        self.w_k = nn.Linear(in_features=in_dim, out_features=qkv_dim)
        self.w_v = nn.Linear(in_features=in_dim, out_features=qkv_dim)
        self.qkv_dim = qkv_dim

    def forward(self, x):
        # 自注意力核心：Q=K=V，均来自同一序列
        q = self.w_q(x)  # [batch, in_dim] -> [batch, qkv_dim]
        k = self.w_k(x)  # [batch, in_dim] -> [batch, qkv_dim]
        v = self.w_v(x)  # [batch, in_dim] -> [batch, qkv_dim]

        # 1. 计算注意力权重
        attention_weights = torch.matmul(q, k.transpose(-1, -2))  # [batch, batch]
        attention_weights = attention_weights / torch.sqrt(torch.tensor(self.qkv_dim, dtype=torch.float32))
        attention_weights = F.softmax(attention_weights, dim=-1)  # 对自身序列维度归一化

        # 2. 加权求和得到输出
        output = torch.matmul(attention_weights, v)  # [batch, qkv_dim]
        return output

if __name__ == '__main__':
    print("\n=== 自注意力测试 ===")
    # 自注意力：输入为同一序列（2个样本，1024维特征）
    x = torch.randn(2, 1024)
    self_attn = SelfAttention()
    self_output = self_attn(x)
    print(f"自注意力输入形状：{x.shape}")
    print(f"自注意力输出形状：{self_output.shape}")  # [2, 768]

---

2.交叉注意力

核心思路：实现数学模型中的步骤

实现过程：

1.QKV的全连接初始化**（交叉注意力的Q来自观察者，K/V来自被观察者）**

2.softmax(Q*(K的转置)/缩放系数) = score的实现

3.score*V 加权求和得到结果

代码实现：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
@Project ：deep_learning
@File ：test.py
@IDE ：PyCharm
@Author ：wjj
@Date ：2025/12/28 21:45
@Description:
"""
import torch
from torch import nn
from torch.nn import functional as F

class CrossAttention(nn.Module):
    def __init__(self, in_dim=1024, qk_dim=768, v_dim=128):
        super(CrossAttention, self).__init__()
        # 线性层输入维度改为可配置，提升灵活性
        self.w_q = nn.Linear(in_features=in_dim, out_features=qk_dim)
        self.w_k = nn.Linear(in_features=in_dim, out_features=qk_dim)
        self.w_v = nn.Linear(in_features=in_dim, out_features=v_dim)
        # 缩放因子改为普通整数，避免GPU/CPU设备不匹配问题
        self.qk_dim = qk_dim

    def forward(self, Q, K, V):
        # Q：查询序列（如观察者特征）
        # K/V：键值序列（如被观察者特征，来自另一组序列）
        q = self.w_q(Q)  # [batch_q, in_dim] -> [batch_q, qk_dim]
        k = self.w_k(K)  # [batch_k, in_dim] -> [batch_k, qk_dim]
        v = self.w_v(V)  # [batch_k, in_dim] -> [batch_k, v_dim]

        # 1. 计算注意力权重（点积注意力 + 缩放 + softmax）
        attention_weights = torch.matmul(q, k.transpose(-1, -2))  # [batch_q, batch_k]
        attention_weights = attention_weights / torch.sqrt(torch.tensor(self.qk_dim, dtype=torch.float32))
        attention_weights = F.softmax(attention_weights, dim=-1)  # 对k维度归一化

        # 2. 加权求和得到输出
        output = torch.matmul(attention_weights, v)  # [batch_q, v_dim]
        return output

if __name__ == '__main__':
    ############################### 交叉注意力测试 #####################
    print("=== 交叉注意力测试 ===")
    # Q：观察者（2个样本，每个样本1024维特征）
    observer = torch.randn(2, 1024)
    # K/V：被观察者（3个样本，每个样本1024维特征，与Q来自不同序列）
    subject = torch.randn(3, 1024)

    cross_attn = CrossAttention()
    cross_output = cross_attn(observer, subject, subject)
    print(f"交叉注意力输入Q形状：{observer.shape}")
    print(f"交叉注意力输入K/V形状：{subject.shape}")
    print(f"交叉注意力输出形状：{cross_output.shape}")  # [2, 128]

---

3.多头注意力的实现(详解)

核心思路：

「线性映射→拆分多头→计算注意力→加权求和→拼接多头」

import torch
from torch import nn
from torch.nn import functional as F

class MultiCrossAttention(nn.Module):
    """
    多头交叉注意力模块（Q来自observer，K/V来自subject）
    核心流程：线性映射→拆分多头→计算注意力→加权求和→拼接多头
    """

    def __init__(self, in_feat_dim=1024, qk_dim=768, v_dim=128, num_head=4):
        """
        初始化多头交叉注意力层
        参数说明：
            in_feat_dim: 输入特征的维度（observer和subject的特征维度，需保持一致）
                        即输入张量的最后一维大小，默认1024
            qk_dim: 单个注意力头中，查询（Q）和键（K）的特征维度（d_k）
                    所有头的Q/K总维度 = num_head * qk_dim
            v_dim: 单个注意力头中，值（V）的特征维度（d_v）
                   所有头的V总维度 = num_head * v_dim
            num_head: 注意力头的数量，即拆分的并行注意力计算路径数，默认4
        """
        super(MultiCrossAttention, self).__init__()
        # 保存模块核心参数（后续前向传播需使用）
        self.in_feat_dim = in_feat_dim  # 输入特征维度
        self.num_head = num_head        # 注意力头数量
        self.qk_dim = qk_dim            # 单个头的Q/K维度
        self.v_dim = v_dim              # 单个头的V维度

        # 定义Q/K/V对应的线性映射层（将输入特征映射到对应多头维度）
        # 线性层输出维度：单个头维度 * 头数（实现多头的并行映射）
        self.w_q = nn.Linear(in_feat_dim, qk_dim * num_head)  # Q的线性映射层
        self.w_k = nn.Linear(in_feat_dim, qk_dim * num_head)  # K的线性映射层
        self.w_v = nn.Linear(in_feat_dim, v_dim * num_head)   # V的线性映射层

        # 保存Q/K的维度标量（用于注意力分数缩放，避免数值爆炸）
        self.d_k = qk_dim

    def forward(self, observer, subject):
        """
        前向传播计算多头交叉注意力
        参数说明：
        :param observer:查询（Q）的输入张量，形状为 (seq_len_q, in_feat_dim)
            seq_len_q: 查询序列长度（即查询样本的数量，如2个观察者）
            in_feat_dim: 输入特征维度（与初始化参数一致）
        :param subject:

        :return:键（K）和值（V）的输入张量，形状为 (seq_len_kv, in_feat_dim)
        seq_len_kv: 键/值序列长度（即被查询样本的数量，如3个被观察者）
        in_feat_dim: 输入特征维度（与observer、初始化参数一致）

        返回值：
            context_vector: 多头注意力拼接后的输出张量，形状为 (seq_len_q, num_head * v_dim)
            即每个查询样本对应一个拼接后的完整特征向量
        """
        # 1. 提取输入序列长度（后续维度重塑需使用）
        # seq_len_q：查询序列长度（observer中的样本数/序列步数）
        # seq_len_kv：键/值序列长度（subject中的样本数/序列步数）
        seq_len_q, _ = observer.shape  # 从observer中提取seq_len_q，忽略第二维特征维度
        seq_len_kv, _ = subject.shape  # 从subject中提取seq_len_kv，忽略第二维特征维度

        # 2. 线性映射：将输入特征转换为Q/K/V张量（映射到多头总维度）
        q = self.w_q(observer)  # 输出形状：(seq_len_q, num_head * qk_dim)
        k = self.w_k(subject)   # 输出形状：(seq_len_kv, num_head * qk_dim)
        v = self.w_v(subject)   # 输出形状：(seq_len_kv, num_head * v_dim)

        # 3. 拆分多头：将多头总维度的张量拆分为单个头的并行张量
        # 重塑维度：(seq_len, num_head, single_head_dim)
        # 含义：[序列长度，注意力头数，单个头的特征维度]
        q = q.reshape(seq_len_q, self.num_head, self.qk_dim)  # Q拆分后形状：(seq_len_q, num_head, qk_dim)
        k = k.reshape(seq_len_kv, self.num_head, self.qk_dim)  # K拆分后形状：(seq_len_kv, num_head, qk_dim)
        v = v.reshape(seq_len_kv, self.num_head, self.v_dim)  # V拆分后形状：(seq_len_kv, num_head, v_dim)

        # 4. 调整维度顺序：便于多头并行计算注意力（将头数维度提前）
        # 调整后形状：(num_head, seq_len, single_head_dim)
        # 含义：[注意力头数，序列长度，单个头的特征维度]
        # 优势：每个头可以独立进行矩阵运算，无需额外循环，提升计算效率
        q = q.permute(1, 0, 2)  # Q调整后形状：(num_head, seq_len_q, qk_dim)
        k = k.permute(1, 0, 2)  # K调整后形状：(num_head, seq_len_kv, qk_dim)
        v = v.permute(1, 0, 2)  # V调整后形状：(num_head, seq_len_kv, v_dim)

        # 5. 计算注意力权重softmax（Q @ K^T / sqrt(d_k)）
        # 形状不变：(num_head, seq_len_q, seq_len_kv)
        attention_scores = torch.matmul(q, k.transpose(-1, -2))
        attention_scores = attention_scores / torch.sqrt(torch.tensor(self.d_k, dtype=torch.float32))
        attention_weights = F.softmax(attention_scores, dim=-1)

        # 6. 加权求和：用注意力权重对V进行加权，得到每个查询的上下文向量
        #attention_weights:(num_head, seq_len_q, seq_len_kv),V:(num_head, seq_len_kv, v_dim)
        # 矩阵乘法后形状：(num_head, seq_len_q, v_dim)
        # 含义：[注意力头数，查询序列长度，单个头的V维度]，每个头独立得到查询的上下文特征
        context_vector = torch.matmul(attention_weights, v)

        # 7. 拼接多头：将多个头的上下文向量拼接为单路完整特征（恢复为常规张量格式）
        # 7.1 调整维度顺序：将头数维度放回中间，形状从(num_head, seq_len_q, v_dim) → (seq_len_q, num_head, v_dim)
        context_vector = context_vector.permute(1, 0, 2)

        # 最终输出形状：(seq_len_q, num_head * v_dim)
        context_vector = context_vector.reshape(seq_len_q, self.num_head * self.v_dim)

        return context_vector


if __name__ == '__main__':
    # 构造测试输入
    # observer：查询输入，形状(seq_len_q, in_feat_dim)
    # 其中：seq_len_q=2（2个查询样本/观察者），in_feat_dim=1024（输入特征维度）
    observer = torch.randn((2, 1024))

    # subject：键/值输入，形状(seq_len_kv, in_feat_dim)
    # 其中：seq_len_kv=3（3个键/值样本/被观察者），in_feat_dim=1024（输入特征维度，与observer一致）
    subject = torch.randn((3, 1024))

    # 初始化多头交叉注意力模块（使用默认参数）
    attention_module = MultiCrossAttention()

    # 前向传播计算
    output = attention_module(observer, subject)

    # 打印输出形状及参数说明
    print("输出张量形状：", output.shape)
    print("形状说明：(seq_len_q, num_head * v_dim) = (2, 4 * 128) = (2, 512)")

---

总结：

本章主要讲解的是注意力机制中，其起源和注意力函数以及自注意力，交叉注意力以及多头注意力及其具体的实现过程，在之后的章节我们将继续学习运用注意力模块在实践中的运用。