
⚡ CYBER_PROFILE ⚡
/// SYSTEM READY ///
WARNING \]: DETECTING HIGH ENERGY
**🌊 🌉 🌊 心手合一 · 水到渠成**

|------------------------------------------------------------------------------------|--------------------------------------------------------------------------------------------------------------|
| **\>\>\> ACCESS TERMINAL \<\<\<** ||
| [**\[ 🦾 作者主页 \]**](https://blog.csdn.net/fengtinghuqu520?spm=1000.2115.3001.5343) | [**\[ 🔥 C语言核心 \]**](https://blog.csdn.net/fengtinghuqu520/category_12955956.html) |
| [**\[ 💾 编程百度 \]**](https://blog.csdn.net/fengtinghuqu520/category_13083835.html) | [**\[ 📡 代码仓库 \]**](https://blog.csdn.net/fengtinghuqu520/article/details/147275999?spm=1001.2014.3001.5502) |
---------------------------------------
Running Process: 100% \| Latency: 0ms
*** ** * ** ***
🚩在之前的`树`的章节中我们讲解了**树这个数据结构的一些基本概念** ,本章我们将重点介绍树结构中最常见的**二叉树**
> 🔗[Lucy的空间骇客裂缝:树](https://blog.csdn.net/fengtinghuqu520/article/details/156150995?spm=1011.2415.3001.10575&sharefrom=mp_manage_link)
#### 索引与导读
* [🤔一、什么是二叉树?](#🤔一、什么是二叉树?)
* [🤔二、二叉树的情况分布](#🤔二、二叉树的情况分布)
* [🤔三、特殊二叉树](#🤔三、特殊二叉树)
*
* [满二叉树](#满二叉树)
* [完全二叉树](#完全二叉树)
* [🤔四、二叉树的性质](#🤔四、二叉树的性质)
*
* [二叉树的普通性质(所有二叉树适用)](#二叉树的普通性质(所有二叉树适用))
*
* [性质 1:第 i i i 层上的结点数](#性质 1:第 i i i 层上的结点数)
* [证明(数学归纳法):](#证明(数学归纳法):)
* [性质 2:深度为 k k k 的最大结点总数](#性质 2:深度为 k k k 的最大结点总数)
* [性质 3:叶子结点与度为2结点的关系 【考研/面试高频】](#性质 3:叶子结点与度为2结点的关系 【考研/面试高频】)
* [完全二叉树的特有性质](#完全二叉树的特有性质)
*
* [性质 4:完全二叉树的深度](#性质 4:完全二叉树的深度)
* [性质5:完全二叉树的数组存储特性](#性质5:完全二叉树的数组存储特性)
* [经典例题](#经典例题)
*
* [1. 叶子结点与度为2结点的关系](#1. 叶子结点与度为2结点的关系)
* [2. 顺序存储结构的适用性](#2. 顺序存储结构的适用性)
* [3. 完全二叉树的叶子结点推导](#3. 完全二叉树的叶子结点推导)
* [4. 完全二叉树的高度计算](#4. 完全二叉树的高度计算)
* [5. 大规模完全二叉树的叶子计算](#5. 大规模完全二叉树的叶子计算)
* [总结技巧](#总结技巧)
* [🤔五、二叉树的存储结构](#🤔五、二叉树的存储结构)
*
*
* [5.1)顺序存储](#5.1)顺序存储)
* [5.2)链式存储](#5.2)链式存储)
*
* [5.2.1)二叉树的遍历方式](#5.2.1)二叉树的遍历方式)
*
* [1)前序遍历](#1)前序遍历)
* [2)中序遍历](#2)中序遍历)
* [3)后序遍历](#3)后序遍历)
* [4)层序遍历](#4)层序遍历)
* [5.2.2)🔨二叉树遍历的经典例题](#5.2.2)🔨二叉树遍历的经典例题)
*
*
* [🎯 第一题:完全二叉树的序列转化](#🎯 第一题:完全二叉树的序列转化)
* [🎯 第二题:秒杀根节点(送分题)](#🎯 第二题:秒杀根节点(送分题))
* [🎯 第三题:由中序与后序还原前序(经典难点)](#🎯 第三题:由中序与后序还原前序(经典难点))
* [🤔六、二叉树的分文件编写](#🤔六、二叉树的分文件编写)
*
* [BinaryTree.h](#BinaryTree.h)
* [BinaryTree.c](#BinaryTree.c)
*
* [简易队列的创建(用于 LevelOrder 和 BinaryTreeComplete)](#简易队列的创建(用于 LevelOrder 和 BinaryTreeComplete))
*
* [1)结构体的创建](#1)结构体的创建)
* [2)初始化队列](#2)初始化队列)
* [3)入队](#3)入队)
* [4)出队](#4)出队)
* [5)获取队头元素](#5)获取队头元素)
* [6)判断队列是否为空](#6)判断队列是否为空)
* [7)销毁队列](#7)销毁队列)
* [🌠创建新节点](#🌠创建新节点)
* [🌠通过前序数组构建二叉树](#🌠通过前序数组构建二叉树)
* [🌠二叉树销毁 (后序遍历销毁)](#🌠二叉树销毁 (后序遍历销毁))
* [🌠节点个数](#🌠节点个数)
* [🌠叶子节点个数(递归实现)](#🌠叶子节点个数(递归实现))
* [🌠第k层节点个数](#🌠第k层节点个数)
* [🌠查找值为x的节点](#🌠查找值为x的节点)
* [🌠前序遍历: 根 -\> 左 -\> 右](#🌠前序遍历: 根 -> 左 -> 右)
* [🌠中序遍历: 左 -\> 根 -\> 右](#🌠中序遍历: 左 -> 根 -> 右)
* [🌠后序遍历: 左 -\> 右 -\> 根](#🌠后序遍历: 左 -> 右 -> 根)
* [🌠层序遍历 (使用队列)](#🌠层序遍历 (使用队列))
* [🌠判断是否为完全二叉树](#🌠判断是否为完全二叉树)
* [🌠二叉树的高度](#🌠二叉树的高度)
* [🖊完整代码](#🖊完整代码)
* [test.c](#test.c)
* [🤔关于二叉树的在线OJ题](#🤔关于二叉树的在线OJ题)
* [💻结尾--- 核心连接协议](#💻结尾— 核心连接协议)
## 🤔一、什么是二叉树?
🚩二叉树(Binary Tree)是 n n n 个节点的有限集合。在 C 语言中,我们通常通过**结构体(struct)**和**指针**来模拟这种非线性的逻辑结构
* 一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 由一个根结点加上两棵别称为左子树和右子树的二叉树组成
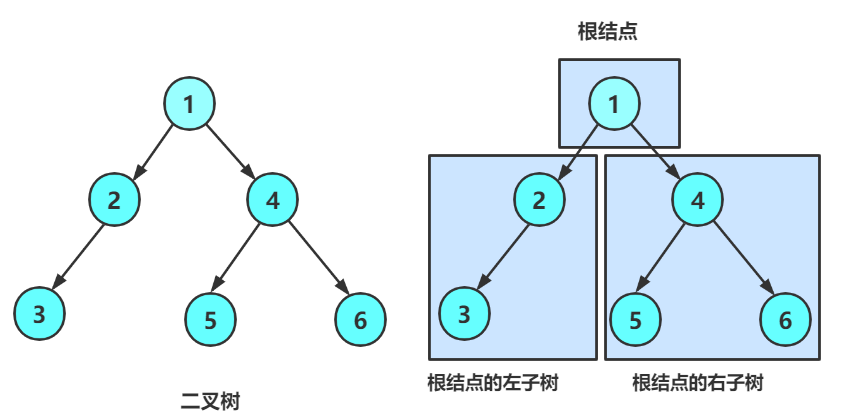
**从上图我们可以看出:**
🚩二叉树不存在度大于2的结点
🚩二叉树的子树有左右之分,次序不能颠倒
> **因此二叉树是有序树**
*** ** * ** ***
## 🤔二、二叉树的情况分布
🚩对于任意二叉树,**都是由以下几种情况复合而成的** :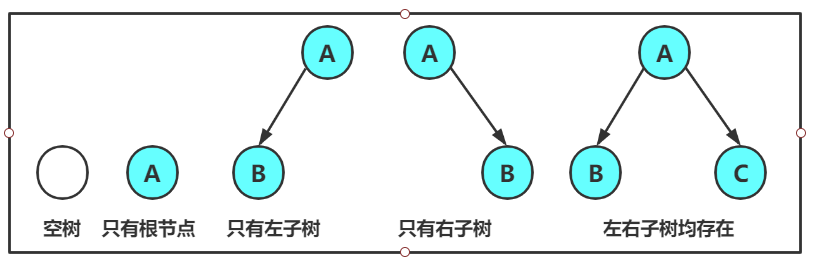
*** ** * ** ***
## 🤔三、特殊二叉树
在普通二叉树中,节点的位置比较随意
但在**满二叉树** 和**完全二叉树** 中,节点的分布遵循严格的规律
这种规律使得我们可以**用数组来高效存储二叉树** ,而不需要总是依赖**链表**
### 满二叉树
**定义**:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树
* **核心公式**
假设树的高度为 h h h(从1开始计数):
* 第 i i i 层的节点数: 2 i − 1 2\^{i-1} 2i−1
* 总节点数 N N N: 2 h − 1 2\^h - 1 2h−1
* **💡 面试考点:**
**如果已知节点总数 N N N 是偶数,它一定不是满二叉树**
* **图解示例**
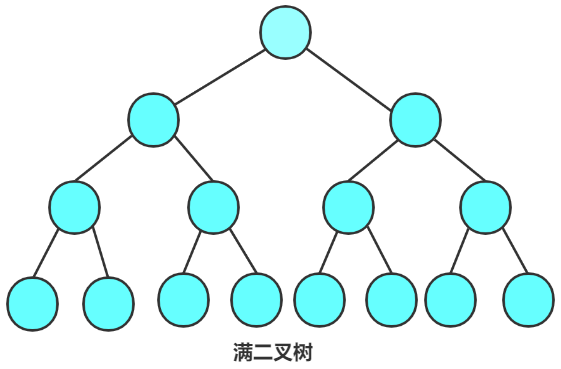
### 完全二叉树
* **定义:**
完全二叉树是效率很高的数据结构,对于深度为 h h h 的二叉树,前 h − 1 h-1 h−1 层必须是满的
第 h h h 层(最后一层)的节点必须从左到右连续排列,中间不能留空
> 满二叉树一定是完全二叉树,但反之不成立
> 完全二叉树允许最后一层没填满,但必须紧凑地靠在左边
* **图解示例**
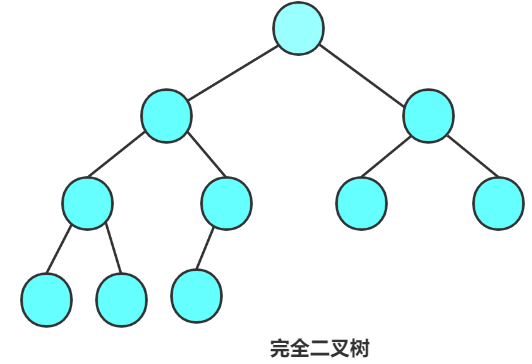
*** ** * ** ***
## 🤔四、二叉树的性质
### 二叉树的普通性质(所有二叉树适用)
这是二叉树通用的三大性质,无论是满二叉树、完全二叉树还是普通二叉树,都必须遵循。
#### 性质 1:第 i i i 层上的结点数
> **结论** :二叉树的第 i i i 层上至多有 2 i − 1 2\^{i-1} 2i−1 个结点 ( i ≥ 1 i \\ge 1 i≥1)。
#### 证明(数学归纳法):
1. **基础步骤** :当 i = 1 i=1 i=1 时,第1层只有根结点,结点数为 1 = 2 1 − 1 = 2 0 1 = 2\^{1-1} = 2\^0 1=21−1=20,命题成立。
2. **归纳假设** :假设第 i − 1 i-1 i−1 层至多有 2 i − 2 2\^{i-2} 2i−2 个结点。
3. **推导** :根据二叉树定义,每个结点最多有两个孩子。因此,第 i i i 层的结点数最多是第 i − 1 i-1 i−1 层结点数的 2 倍。
M a x ( N i ) = 2 × M a x ( N i − 1 ) = 2 × 2 i − 2 = 2 i − 1 Max(N_i) = 2 \\times Max(N_{i-1}) = 2 \\times 2\^{i-2} = 2\^{i-1} Max(Ni)=2×Max(Ni−1)=2×2i−2=2i−1
**证毕。**
*** ** * ** ***
#### 性质 2:深度为 k k k 的最大结点总数
> **结论** :深度为 k k k 的二叉树至多有 2 k − 1 2\^k - 1 2k−1 个结点 ( k ≥ 1 k \\ge 1 k≥1)。
* **证明(等比数列求和):**
深度为 k k k 的二叉树,要想结点最多,那么每一层都必须达到最大值(即满二叉树)。
根据性质1,各层最大结点数分别为: 2 0 , 2 1 , 2 2 , . . . , 2 k − 1 2\^0, 2\^1, 2\^2, ..., 2\^{k-1} 20,21,22,...,2k−1。
总数 S k S_k Sk 为:
S k = ∑ i = 1 k 2 i − 1 = 2 0 + 2 1 + ⋯ + 2 k − 1 S_k = \\sum_{i=1}\^{k} 2\^{i-1} = 2\^0 + 2\^1 + \\dots + 2\^{k-1} Sk=i=1∑k2i−1=20+21+⋯+2k−1
根据等比数列求和公式:
S k = a 1 ( 1 − q k ) 1 − q = 1 ( 1 − 2 k ) 1 − 2 = 2 k − 1 S_k = \\frac{a_1(1-q\^k)}{1-q} = \\frac{1(1-2\^k)}{1-2} = 2\^k - 1 Sk=1−qa1(1−qk)=1−21(1−2k)=2k−1
**证毕。**
*** ** * ** ***
#### 性质 3:叶子结点与度为2结点的关系 【考研/面试高频】
> **结论** :对任何一棵二叉树 T T T,如果其叶子结点(度为0)数为 n 0 n_0 n0,度为2的结点数为 n 2 n_2 n2,则 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1。
* **详细推导:**
这是一个非常精妙的推导,利用了"结点数"和"分支数(边数)"的两个等式。
**设:**
* n n n 为二叉树结点总数。
* n 0 n_0 n0 为度为0的结点数(叶子)。
* n 1 n_1 n1 为度为1的结点数。
* n 2 n_2 n2 为度为2的结点数。
* B B B 为分支总数(即树枝/边的数量)。
**步骤 1:从结点组成看总数**
二叉树只有三种类型的结点(度为0, 1, 2),所以:
n = n 0 + n 1 + n 2 ------ (式1) n = n_0 + n_1 + n_2 \\quad \\text{------ (式1)} n=n0+n1+n2------ (式1)
**步骤 2:从分支(边)看总数**
* 除了根结点外,每个结点都有且仅有一条边从上面连下来。
* 所以,结点总数 = 分支总数 + 1(根结点)。
n = B + 1 ------ (式2) n = B + 1 \\quad \\text{------ (式2)} n=B+1------ (式2)
**步骤 3:计算分支总数 B B B**
* 度为0的结点发出 0 条边。
* 度为1的结点发出 1 条边。
* 度为2的结点发出 2 条边。
B = 0 × n 0 + 1 × n 1 + 2 × n 2 = n 1 + 2 n 2 B = 0 \\times n_0 + 1 \\times n_1 + 2 \\times n_2 = n_1 + 2n_2 B=0×n0+1×n1+2×n2=n1+2n2
**步骤 4:联立求解**
将 B B B 代入 (式2):
n = n 1 + 2 n 2 + 1 ------ (式3) n = n_1 + 2n_2 + 1 \\quad \\text{------ (式3)} n=n1+2n2+1------ (式3)
联立 (式1) 和 (式3):
n 0 + n 1 + n 2 = n 1 + 2 n 2 + 1 n_0 + n_1 + n_2 = n_1 + 2n_2 + 1 n0+n1+n2=n1+2n2+1
消去 n 1 n_1 n1:
n 0 + n 2 = 2 n 2 + 1 n_0 + n_2 = 2n_2 + 1 n0+n2=2n2+1
移项得:
n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1
**证毕。**
> **注意** :这个性质告诉我们,**二叉树的叶子结点数只和度为2的结点数有关**,与度为1的结点数无关。
*** ** * ** ***
### 完全二叉树的特有性质
**完全二叉树 (Complete Binary Tree)** 是效率极高的一种特殊二叉树(堆就是完全二叉树),它有两个额外的核心性质。
#### 性质 4:完全二叉树的深度
> **结论** :具有 n n n 个结点的完全二叉树的深度 k k k 为 ⌊ log 2 n ⌋ + 1 \\lfloor \\log_2 n \\rfloor + 1 ⌊log2n⌋+1 或 ⌈ log 2 ( n + 1 ) ⌉ \\lceil \\log_2(n+1) \\rceil ⌈log2(n+1)⌉。
> *(注: ⌊ x ⌋ \\lfloor x \\rfloor ⌊x⌋ 表示向下取整)*
* **证明:**
假设完全二叉树深度为 k k k。
1. 根据性质2,深度为 k k k 的满二叉树有 2 k − 1 2\^k - 1 2k−1 个结点。
2. 深度为 k − 1 k-1 k−1 的满二叉树有 2 k − 1 − 1 2\^{k-1} - 1 2k−1−1 个结点。
3. 完全二叉树的结点数 n n n 介于两者之间(第 k k k 层至少有1个结点,至多排满):
2 k − 1 − 1 \< n ≤ 2 k − 1 2\^{k-1} - 1 \< n \\le 2\^k - 1 2k−1−1\ 0 i \> 0 i\>0,则 i i i 位置结点的双亲(父结点)序号为: ⌊ ( i − 1 ) / 2 ⌋ \\lfloor (i-1)/2 \\rfloor ⌊(i−1)/2⌋;
* 若 i = 0 i = 0 i=0, i i i 为根结点编号,无双亲结点。
2. **左孩子序号**:
* 若 2 i + 1 \< n 2i + 1 \< n 2i+1\ **正确答案:B**
**【详细解析】**
这是一道考察二叉树通用性质的题目。
根据二叉树的性质 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1(即:叶子结点数 = 度为2的结点数 + 1):
* 已知 n 2 = 199 n_2 = 199 n2=199
* 则 n 0 = 199 + 1 = 200 n_0 = 199 + 1 = 200 n0=199+1=200
**验证合法性(排除A):**
总结点数 n = n 0 + n 1 + n 2 n = n_0 + n_1 + n_2 n=n0+n1+n2。
399 = 200 + n 1 + 199 399 = 200 + n_1 + 199 399=200+n1+199
399 = 399 + n 1 ⇒ n 1 = 0 399 = 399 + n_1 \\Rightarrow n_1 = 0 399=399+n1⇒n1=0
度为1的结点数为0,这是一个合法的二叉树(实际上这是一棵满二叉树或正则二叉树)。
故选 **B**。
*** ** * ** ***
#### 2. 顺序存储结构的适用性
**题目描述:**
下列数据结构中,不适合采用顺序存储结构的是( )
A. 非完全二叉树
B. 堆
C. 队列
D. 栈
> **正确答案:A**
**【详细解析】**
* **A. 非完全二叉树** :如果在数组(顺序存储)中存储非完全二叉树,为了保持节点间的父子下标关系(即父节点 i i i 的左孩子为 2 i 2i 2i,右孩子为 2 i + 1 2i+1 2i+1),必须在数组中留出空位来代表"缺失"的节点。这会导致大量的空间浪费(稀疏),因此通常采用**链式存储**。
* **B. 堆**:堆在逻辑上是一棵完全二叉树,在数组中存储时紧凑且无空间浪费,非常适合顺序存储。
* **C. 队列 \& D. 栈**:作为线性表,顺序存储(数组)是它们的标准实现方式之一。
故选 **A**。
*** ** * ** ***
#### 3. 完全二叉树的叶子结点推导
**题目描述:**
在具有 2 n 2n 2n 个结点的完全二叉树中,叶子结点个数为( )
A. n n n
B. n + 1 n+1 n+1
C. n − 1 n-1 n−1
D. n / 2 n/2 n/2
> **正确答案:A**
**【详细解析】**
**方法一:利用奇偶性分析**
1. 设总结点数为 N = 2 n N = 2n N=2n,这是一个**偶数**。
2. 我们知道 N = n 0 + n 1 + n 2 N = n_0 + n_1 + n_2 N=n0+n1+n2。
3. 代入性质 n 2 = n 0 − 1 n_2 = n_0 - 1 n2=n0−1,得:
N = n 0 + n 1 + ( n 0 − 1 ) = 2 n 0 + n 1 − 1 N = n_0 + n_1 + (n_0 - 1) = 2n_0 + n_1 - 1 N=n0+n1+(n0−1)=2n0+n1−1
4. 在完全二叉树中,度为1的结点数 n 1 n_1 n1 只能是 **0** 或 **1** 。
* 若 n 1 = 0 n_1 = 0 n1=0,则 N = 2 n 0 − 1 N = 2n_0 - 1 N=2n0−1(结果为奇数)。
* 若 n 1 = 1 n_1 = 1 n1=1,则 N = 2 n 0 N = 2n_0 N=2n0(结果为偶数)。
5. 因为题目给出总结点数 2 n 2n 2n 是**偶数** ,所以必然满足 n 1 = 1 n_1 = 1 n1=1 的情况。
6. 方程变为: 2 n = 2 n 0 ⇒ n 0 = n 2n = 2n_0 \\Rightarrow n_0 = n 2n=2n0⇒n0=n。
**方法二:公式法**
对于完全二叉树,叶子结点数 n 0 = ⌈ N / 2 ⌉ n_0 = \\lceil N/2 \\rceil n0=⌈N/2⌉ (向上取整)。
n 0 = ⌈ 2 n / 2 ⌉ = n n_0 = \\lceil 2n / 2 \\rceil = n n0=⌈2n/2⌉=n。
故选 **A**。
*** ** * ** ***
#### 4. 完全二叉树的高度计算
**题目描述:**
一棵完全二叉树的结点数位为 531 个,那么这棵树的高度为( )
A. 11
B. 10
C. 8
D. 12
> **正确答案:B**
**【详细解析】**
根据完全二叉树高度公式: h = ⌊ log 2 N ⌋ + 1 h = \\lfloor \\log_2 N \\rfloor + 1 h=⌊log2N⌋+1。
1. 我们需要找到 531 介于 2 的哪两个幂次方之间。
2. 2 9 = 512 2\^9 = 512 29=512
3. 2 10 = 1024 2\^{10} = 1024 210=1024
4. 因为 512 \< 531 \< 1024 512 \< 531 \< 1024 512\<531\<1024,即 2 9 \< 531 \< 2 10 2\^9 \< 531 \< 2\^{10} 29\<531\<210。
5. 所以 ⌊ log 2 531 ⌋ = 9 \\lfloor \\log_2 531 \\rfloor = 9 ⌊log2531⌋=9。
6. 高度 h = 9 + 1 = 10 h = 9 + 1 = 10 h=9+1=10。
故选 **B**。
*** ** * ** ***
#### 5. 大规模完全二叉树的叶子计算
**题目描述:**
一个具有 767 个结点的完全二叉树,其叶子结点个数为( )
> **正确答案:384**
**【详细解析】**
**方法一:奇偶判断法**
1. 总结点数 N = 767 N = 767 N=767 是**奇数**。
2. 根据 N = 2 n 0 + n 1 − 1 N = 2n_0 + n_1 - 1 N=2n0+n1−1,要使 N N N 为奇数,则 n 1 n_1 n1 必须为 0(若 n 1 = 1 n_1=1 n1=1 则 N N N 为偶数)。
3. 所以: 767 = 2 n 0 − 1 767 = 2n_0 - 1 767=2n0−1
4. 2 n 0 = 768 2n_0 = 768 2n0=768
5. n 0 = 384 n_0 = 384 n0=384
**方法二:临界点法**
在完全二叉树中,最后一个非叶子结点的编号为 ⌊ N / 2 ⌋ \\lfloor N/2 \\rfloor ⌊N/2⌋。
* 最后一个非叶子结点索引 = ⌊ 767 / 2 ⌋ = 383 \\lfloor 767 / 2 \\rfloor = 383 ⌊767/2⌋=383。
* 叶子结点就是编号大于 383 的所有结点。
* 叶子数 = 总数 - 非叶子数 = 767 − 383 = 384 767 - 383 = 384 767−383=384。
*** ** * ** ***
#### 总结技巧
做二叉树选择题时,牢记以下三个核心工具:
* 🚩1. **通用公式** : n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1 (适用所有二叉树)
* 🚩2. **完全二叉树判定** : n 1 ∈ { 0 , 1 } n_1 \\in \\{0, 1\\} n1∈{0,1},且 N N N 为偶数时 n 1 = 1 n_1=1 n1=1,N为奇数时 n 1 = 0 n_1=0 n1=0。
* 🚩3. **高度估算** :熟记 2 10 = 1024 2\^{10}=1024 210=1024, 2 8 = 256 2\^8=256 28=256 等关键数值。
*** ** * ** ***
## 🤔五、二叉树的存储结构
二叉树一般可以使用两种结构存储,一种`顺序结构`,一种`链式结构`
> 普通的二叉树是不适合用**数组** 来存储的,因为可能会存在大量的空间浪费
>
> 而完全二叉树更适合使用**顺序结构** 存储
> 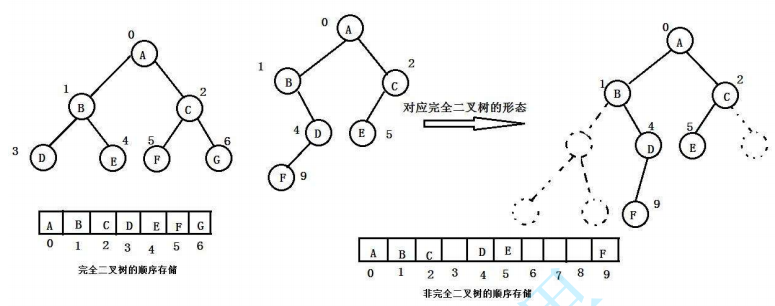
>
> **现实中我们通常把`堆(一种二叉树)`使用`顺序结构的数组`来存储**
* 对于**完全二叉树**,我们可以直接将其节点按层序编号,存储在数组中
* 对于**一般二叉树** ,为了保持节点间的逻辑关系,我们需要**在数组中将其"补"成完全二叉树,不存在的节点在数组中用"空"(如 0 或特殊符号)表示**
*** ** * ** ***
#### 5.1)顺序存储
🚩二叉树的顺序存储结构是指利用**一组地址连续的存储单元** (通常是**数组** )依次`自上而下`、`自左至右`存储完全二叉树上的结点元素
> 现实中我们通常把 **堆(一种二叉树)** 使用`顺序结构的数组`来存储
>
> 🔗[Lucy的空间骇客裂缝:堆](https://blog.csdn.net/fengtinghuqu520/article/details/156204209)
非完全二叉树不适合用`顺序存储`,因为会**造成大量的空间浪费**
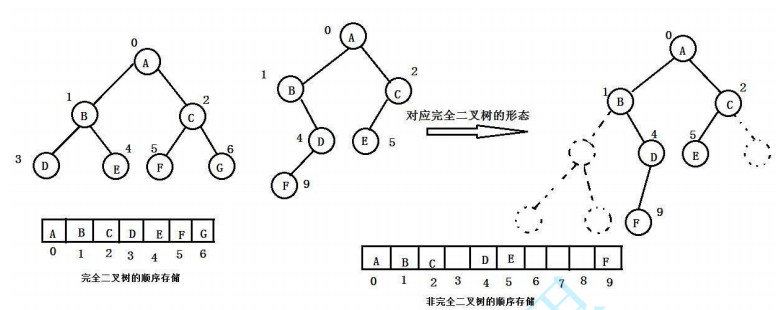
*** ** * ** ***
#### 5.2)链式存储
* **链式结构节点的定义**
```c
typedef int BTDataType;
typedef struct BinaryTreeNode {
BTDataType data;
struct BinaryTreeNode* right;
struct BinaryTreeNode* left;
}BTNode;
```
🚩`data`------*当前节点的值域*
🚩`left`------*左孩子节点*
🚩`right`------*右孩子节点*
*** ** * ** ***
##### 5.2.1)二叉树的遍历方式
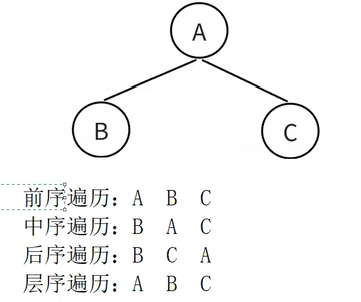
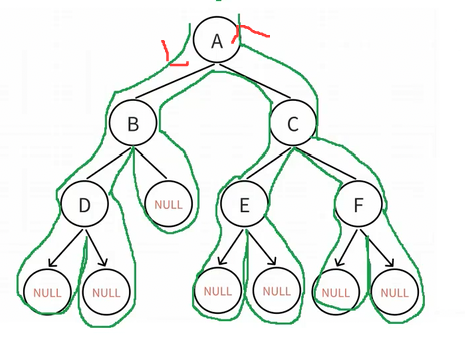
###### 1)前序遍历
先遍历根节点,再遍历左子树,最后遍历右子树---**根左右**
A
B
D
NULL
NULL
NULL
C
E
NULL
NULL
F
NULL
NULL
*** ** * ** ***
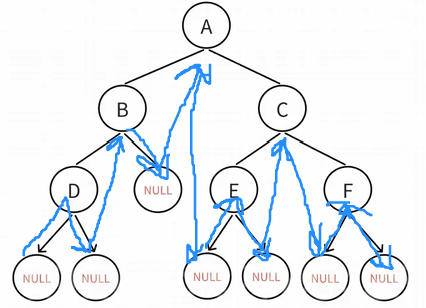
###### 2)中序遍历
先遍历左子树,再遍历根节点,最后遍历右子树---**左根右**
NULL
D
NULL
B
NULL
A
NULL
E
NULL
C
NULL
F
NULL
*** ** * ** ***
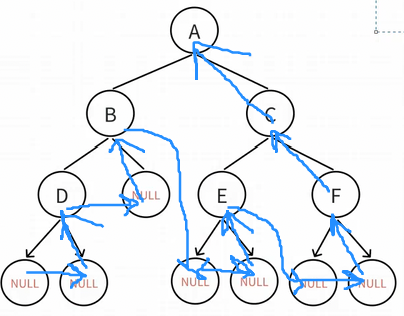
###### 3)后序遍历
先遍历左子树,再遍历右子树,最后遍历根节点---**左右根**
NULL
NULL
D
NULL
B
NULL
NULL
E
NULL
NULL
F
C
A
*** ** * ** ***
###### 4)层序遍历
按照层次依次遍历 **(从上到下,从左到右)**
除了**先序遍历、中序遍历、后序遍历** 外,还可以对二叉树进行**层序遍历**
> 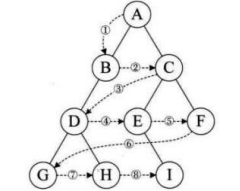
> **设二叉树的根结点所在层数为1**
>
> * 层序遍历就是**从所在二叉树的根结点出发**
> * **首先**访问第一层的树根结点
> * **然后**从左到右访问第2层上的结点
> * **接着**是第三层的结点
> * 以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历
*** ** * ** ***
##### 5.2.2)🔨二叉树遍历的经典例题
###### 🎯 第一题:完全二叉树的序列转化
* **📝 题目描述**
> **某完全二叉树按层次输出(同一层从左到右)的序列为 `ABCDEFGH`
> 该完全二叉树的前序序列为( )**
>
> A. ABDHECFG
>
> B. ABCDEFGH
>
> C. HDBEAFCG
>
> D. HDEBFGCA
*** ** * ** ***
💡 深度解析
**解题核心:完全二叉树的数组下标性质**
完全二叉树最强大的性质在于它可以用数组完美存储。我们可以给层次序列中的每个节点打上编号(从 1 开始):
**Step 1:建立索引映射**
序列 `A B C D E F G H` 对应下标 `1 2 3 4 5 6 7 8`。
**Step 2:利用公式找孩子**
对于完全二叉树中任意节点 i i i:
* **左孩子索引** : 2 i 2i 2i
* **右孩子索引** : 2 i + 1 2i + 1 2i+1
具体推导如下:
* **A (index 1)** → \\rightarrow → 左: 2 2 2 (B), 右: 3 3 3 ©
* **B (index 2)** → \\rightarrow → 左: 4 4 4 (D), 右: 5 5 5 (E)
* **C (index 3)** → \\rightarrow → 左: 6 6 6 (F), 右: 7 7 7 (G)
* **D (index 4)** → \\rightarrow → 左: 8 8 8 (H), 右: 9 9 9 (越界,无右孩子)
* **E, F, G, H** → \\rightarrow → 均为叶子节点
**Step 3:构建逻辑树(Mermaid图解)**
A
B
C
D
E
F
G
H
*** ** * ** ***
###### 🎯 第二题:秒杀根节点(送分题)
* **📝 题目描述**
> **二叉树的先序遍历和中序遍历如下:先序遍历 `EFHIGJK`,中序遍历 `HFIEJKG`。则二叉树根结点为()**
>
> A. E
>
> B. F
>
> C. G
>
> D. H
*** ** * ** ***
**💡 深度解析**
**解题核心:先序遍历的"排头兵"定律**
这道题考察的是对遍历定义的最基本理解,属于"眼疾手快"的送分题。
1. **先序遍历(Pre-order)定义** :
Root → Left → Right \\text{Root} \\rightarrow \\text{Left} \\rightarrow \\text{Right} Root→Left→Right
这行公式告诉我们一个铁律:**先序序列的第一个元素,永远是整棵树的根节点**。
2. **解题步骤**:
* 👀 **看先序序列** :`E F H I G J K`
* 👉 **锁定首位** :第一个字母是 **E**。
* ✅ **得出结论**:整棵树的根节点就是 E。
3. **验算(确保万无一失)** :
在中序序列 `H F I E J K G` 中,我们找到 `E`。
* `E` 左边是 `HFI`(左子树节点)
* `E` 右边是 `JKG`(右子树节点)
* 逻辑完全通畅,答案无误。
✅ 正确答案:A
*** ** * ** ***
###### 🎯 第三题:由中序与后序还原前序(经典难点)
* **📝 题目描述**
**设一棵二叉树的中序遍历序列:`badce`,后序遍历序列:`bdeca`,则二叉树前序遍历序列为____。**
> A. adbce
>
> B. decab
>
> C. debac
>
> D. abcde
*** ** * ** ***
💡 深度解析
**解题核心:后序定根,中序分左右**
这是二叉树考题中的"重头戏",需要利用递归思想进行还原。
**Step 1:确定全局根节点**
* **后序序列** (Left → \\rightarrow → Right → \\rightarrow → Root):`b d e c` **`a`**
* 🎯 序列最后一个元素是 **a** ,所以 **Root = a**。
**Step 2:第一轮切分(中序序列)**
* 在**中序序列** (Left → \\rightarrow → Root → \\rightarrow → Right)中找到 `a`:`b` **`a`** `d c e`
* 👈 **左子树** :`b`(只有一个节点,搞定)
* 👉 **右子树** :`d c e`(这就需要进行下一轮分析)
**Step 3:深入分析右子树**
我们需要确定右子树 `{d, c, e}` 的内部结构:
1. **找右子树的根** :看后序序列中对应这三个节点的部分 → \\rightarrow → `d e c`。
2. **锁定** :后序 `d e` **`c`** 的最后一个是 **c** 。所以,**右子树的根是 c**。
3. **切分右子树** :回到中序序列的右边部分 `d c e`,以 `c` 为中心切分:
* `c` 左边是 `d` → \\rightarrow → **c 的左孩子是 d**
* `c` 右边是 `e` → \\rightarrow → **c 的右孩子是 e**
**Step 4:构建完整的逻辑结构图**
a
b
c
d
e
*** ** * ** ***
## 🤔六、二叉树的分文件编写
> 🔗[Lucy的gitee码云传送门:链式二叉树](https://gitee.com/maple-lake-district/coding/commit/891746b332dc76f50b539d89e89aed3eb0536fc5)
### BinaryTree.h
```c
#pragma once
#include
#include
#include
#include
// 假设树中存储的数据是 int 类型
typedef int BTDataType;
typedef struct BinaryTreeNode {
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
} BTNode;
// --- 核心功能接口 ---
// 创建一个新节点
BTNode* BinaryTreeCreateNode(BTDataType x);
// 通过前序遍历的数组构建二叉树 (假设 '#' 或特定值代表空)
// 注意:这里为了通用性,我们在.c中定义 -1 代表空节点
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树的销毁
void BinaryTreeDestory(BTNode** root);
// 二叉树的节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树的叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树的前序遍历
void PreOrder(BTNode* root);
// 二叉树的中序遍历
void InOrder(BTNode* root);
// 二叉树的后序遍历
void PostOrder(BTNode* root);
// 二叉树的层序遍历
void LevelOrder(BTNode* root);
// 判断二叉树是否为完全二叉树
int BinaryTreeComplete(BTNode* root);
// 获取二叉树的高度/深度
int BinaryTreeHeight(BTNode* root);
```
*** ** * ** ***
### BinaryTree.c
**这里实现了所有逻辑,并包含了一个简易队列用于辅助层序遍历**
*** ** * ** ***
#### 简易队列的创建(用于 LevelOrder 和 BinaryTreeComplete)
> 涉及一些**队列数据结构** 的知识👇
>
> 🔗[Lucy的空间骇客裂缝:栈与队列](https://blog.csdn.net/fengtinghuqu520/article/details/155920754)
*** ** * ** ***
##### 1)结构体的创建
**注意队列里面存储的是树节点的指针**
```c
typedef BTNode* QDataType; // 队列里存的是树节点的指针
```
*** ** * ** ***
```c
typedef struct QueueNode {
QDataType data;
struct QueueNode* next;
} QNode;
typedef struct Queue {
QNode* head;
QNode* tail;
} Queue;
```
*** ** * ** ***
##### 2)初始化队列
```c
void QueueInit(Queue* pq) {
assert(pq);
pq->head = pq->tail = NULL;
}
```
*** ** * ** ***
##### 3)入队
```c
void QueuePush(Queue* pq, QDataType x) {
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL) {
perror("malloc fail");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
if (pq->tail == NULL) {
pq->head = pq->tail = newnode;
} else {
pq->tail->next = newnode;
pq->tail = newnode;
}
}
```
*** ** * ** ***
##### 4)出队
```c
void QueuePop(Queue* pq) {
assert(pq);
assert(pq->head); // 确保队列不为空
QNode* next = pq->head->next;
free(pq->head);
pq->head = next;
if (pq->head == NULL) {
pq->tail = NULL;
}
}
```
*** ** * ** ***
##### 5)获取队头元素
```c
QDataType QueueFront(Queue* pq) {
assert(pq);
assert(pq->head);
return pq->head->data;
}
```
*** ** * ** ***
##### 6)判断队列是否为空
```c
bool QueueEmpty(Queue* pq) {
assert(pq);
return pq->head == NULL;
}
```
*** ** * ** ***
##### 7)销毁队列
```c
void QueueDestroy(Queue* pq) {
assert(pq);
QNode* cur = pq->head;
while (cur) {
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
}
```
*** ** * ** ***
#### 🌠创建新节点
```c
BTNode* BinaryTreeCreateNode(BTDataType x) {
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL) {
perror("malloc fail");
exit(-1);
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
```
**内存分配**
**`BTNode* node = (BTNode*)malloc(sizeof(BTNode));`**
*** ** * ** ***
#### 🌠通过前序数组构建二叉树
```c
//约定:数组中-1代表NULL
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi) {
if (*pi >= n) return NULL;
if (a[*pi] == -1) {
(*pi)++;
return NULL;
}
BTNode* root = BinaryTreeCreateNode(a[*pi]);
(*pi)++;
root->left = BinaryTreeCreate(a, n, pi);
root->right = BinaryTreeCreate(a, n, pi);
return root;
}
```
* **`int* pi`** :指向**当前数组索引的指针** (必须用**指针** ,**保证递归中索引同步递增**)
* **`return NULL;`** :返回`NULL`,告诉父节点这个子节点为空
* **`BTNode* root = BinaryTreeCreateNode(a[*pi]);`** :用当前数组元素`a[*pi]`的值创建节点
**递归创建左右子树**
`root->left = BinaryTreeCreate(a, n, pi);`
`root->right = BinaryTreeCreate(a, n, pi);`
*** ** * ** ***
#### 🌠二叉树销毁 (后序遍历销毁)
```c
void BinaryTreeDestory(BTNode** root) {
assert(root);
if (*root == NULL) return;
BinaryTreeDestory(&((*root)->left));
BinaryTreeDestory(&((*root)->right));
free(*root);
*root = NULL; // 这是一个好习惯,防止野指针
}
```
**二级指针**
**`BTNode** root`** :传入**根节点的地址(指针的地址)** ,遍历整棵树并释放所有节点的内存,最后将根指针设置为 `NULL`
*** ** * ** ***
#### 🌠节点个数
```c
int BinaryTreeSize(BTNode* root) {
return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
```
**`int`和`BTDataType`的区别**
* `int`表示真实数据个数
* `BTDataType`表示二叉树内部的数据
*** ** * ** ***
#### 🌠叶子节点个数(递归实现)
```c
int BinaryTreeLeafSize(BTNode* root) {
if (root == NULL) return 0;
if (root->left == NULL && root->right == NULL) return 1;
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
```
Pass
Yes
No
Yes
No
Start: BinaryTreeLevelKSize
Assert: k \>= 1
root == NULL ?
k == 1 ?
Return 0
Return 1
Return Sum
int left = BinaryTreeLevelKSize(root-\>left, k - 1)
int right = BinaryTreeLevelKSize(root-\>right, k - 1)
Result = left + right
*** ** * ** ***
#### 🌠第k层节点个数
```c
int BinaryTreeLevelKSize(BTNode* root, int k) {
assert(k >= 1);
if (root == NULL) return 0;
if (k == 1) return 1;
return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
```
**递归运算**
`return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);`
时间复杂度:O(k)
*** ** * ** ***
#### 🌠查找值为x的节点
```c
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {
if (root == NULL) return NULL;
if (root->data == x) return root;
BTNode* ret1 = BinaryTreeFind(root->left, x);
if (ret1) return ret1; // 左边找到了就返回,不用找右边了
BTNode* ret2 = BinaryTreeFind(root->right, x);
if (ret2) return ret2;
return NULL;
}
```
*** ** * ** ***
#### 🌠前序遍历: 根 -\> 左 -\> 右
```c
void PreOrder(BTNode* root) {
if (root == NULL) {
printf("NULL ");
return;
}
printf("%d ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}
```
*** ** * ** ***
#### 🌠中序遍历: 左 -\> 根 -\> 右
```c
void InOrder(BTNode* root) {
if (root == NULL) {
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
```
*** ** * ** ***
#### 🌠后序遍历: 左 -\> 右 -\> 根
```c
void PostOrder(BTNode* root) {
if (root == NULL) {
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
```
*** ** * ** ***
#### 🌠层序遍历 (使用队列)
```c
void LevelOrder(BTNode* root) {
if (root == NULL) return;
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q)) {
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
if (front->left) QueuePush(&q, front->left);
if (front->right) QueuePush(&q, front->right);
}
printf("\n");
QueueDestroy(&q);
}
```
*** ** * ** ***
#### 🌠判断是否为完全二叉树
**核心逻辑:** 层序遍历,一旦遇到空节点,后续队列中不能再出现非空节点
```c
int BinaryTreeComplete(BTNode* root) {
if (root == NULL) return 1;
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q)) {
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL) {
break; // 遇到了空节点,跳出这一层循环去检查剩余队列
}
// 不管孩子是不是空,都入队(为了检测是否断层)
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
// 检查队列剩余元素,如果有非空,则不是完全二叉树
while (!QueueEmpty(&q)) {
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL) {
QueueDestroy(&q);
return 0; // 失败
}
}
QueueDestroy(&q);
return 1; // 成功
}
```
*** ** * ** ***
#### 🌠二叉树的高度
```c
int BinaryTreeHeight(BTNode* root) {
if (root == NULL) return 0;
int leftHeight = BinaryTreeHeight(root->left);
int rightHeight = BinaryTreeHeight(root->right);
return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
}
```
*** ** * ** ***
#### 🖊完整代码
```c
#include "BinaryTree.h"
// ==========================================
// 辅助模块:简易队列 (Queue) 实现
// 用于 LevelOrder 和 BinaryTreeComplete
// ==========================================
typedef BTNode* QDataType; // 队列里存的是树节点的指针
typedef struct QueueNode {
QDataType data;
struct QueueNode* next;
} QNode;
typedef struct Queue {
QNode* head;
QNode* tail;
} Queue;
// 初始化队列
void QueueInit(Queue* pq) {
assert(pq);
pq->head = pq->tail = NULL;
}
// 入队
void QueuePush(Queue* pq, QDataType x) {
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL) {
perror("malloc fail");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
if (pq->tail == NULL) {
pq->head = pq->tail = newnode;
} else {
pq->tail->next = newnode;
pq->tail = newnode;
}
}
// 出队
void QueuePop(Queue* pq) {
assert(pq);
assert(pq->head); // 确保队列不为空
QNode* next = pq->head->next;
free(pq->head);
pq->head = next;
if (pq->head == NULL) {
pq->tail = NULL;
}
}
// 获取队头元素
QDataType QueueFront(Queue* pq) {
assert(pq);
assert(pq->head);
return pq->head->data;
}
// 判断队列是否为空
bool QueueEmpty(Queue* pq) {
assert(pq);
return pq->head == NULL;
}
// 销毁队列
void QueueDestroy(Queue* pq) {
assert(pq);
QNode* cur = pq->head;
while (cur) {
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
}
// ==========================================
// 二叉树核心功能实现
// ==========================================
// 创建新节点
BTNode* BinaryTreeCreateNode(BTDataType x) {
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL) {
perror("malloc fail");
exit(-1);
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
// 通过前序数组构建二叉树
// 约定:数组中 -1 代表 NULL
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi) {
if (*pi >= n) return NULL;
// 这里的 -1 是我们约定的空节点值
if (a[*pi] == -1) {
(*pi)++;
return NULL;
}
BTNode* root = BinaryTreeCreateNode(a[*pi]);
(*pi)++;
root->left = BinaryTreeCreate(a, n, pi);
root->right = BinaryTreeCreate(a, n, pi);
return root;
}
// 二叉树销毁 (后序遍历销毁)
void BinaryTreeDestory(BTNode** root) {
assert(root);
if (*root == NULL) return;
BinaryTreeDestory(&((*root)->left));
BinaryTreeDestory(&((*root)->right));
free(*root);
*root = NULL; // 这是一个好习惯,防止野指针
}
// 节点个数
int BinaryTreeSize(BTNode* root) {
return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
// 叶子节点个数
int BinaryTreeLeafSize(BTNode* root) {
if (root == NULL) return 0;
if (root->left == NULL && root->right == NULL) return 1;
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
// 第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k) {
assert(k >= 1);
if (root == NULL) return 0;
if (k == 1) return 1;
// 子问题的思路:求左树的k-1层 + 右树的k-1层
return BinaryTreeLevelKSize(root->left, k - 1)
+ BinaryTreeLevelKSize(root->right, k - 1);
}
// 查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {
if (root == NULL) return NULL;
if (root->data == x) return root;
BTNode* ret1 = BinaryTreeFind(root->left, x);
if (ret1) return ret1; // 左边找到了就返回,不用找右边了
BTNode* ret2 = BinaryTreeFind(root->right, x);
if (ret2) return ret2;
return NULL;
}
// 前序遍历: 根 -> 左 -> 右
void PreOrder(BTNode* root) {
if (root == NULL) {
printf("NULL ");
return;
}
printf("%d ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}
// 中序遍历: 左 -> 根 -> 右
void InOrder(BTNode* root) {
if (root == NULL) {
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
// 后序遍历: 左 -> 右 -> 根
void PostOrder(BTNode* root) {
if (root == NULL) {
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
// 层序遍历 (使用队列)
void LevelOrder(BTNode* root) {
if (root == NULL) return;
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q)) {
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
if (front->left) QueuePush(&q, front->left);
if (front->right) QueuePush(&q, front->right);
}
printf("\n");
QueueDestroy(&q);
}
// 判断是否为完全二叉树
// 核心逻辑:层序遍历,一旦遇到空节点,后续队列中不能再出现非空节点
int BinaryTreeComplete(BTNode* root) {
if (root == NULL) return 1;
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q)) {
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL) {
break; // 遇到了空节点,跳出这一层循环去检查剩余队列
}
// 不管孩子是不是空,都入队(为了检测是否断层)
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
// 检查队列剩余元素,如果有非空,则不是完全二叉树
while (!QueueEmpty(&q)) {
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL) {
QueueDestroy(&q);
return 0; // 失败
}
}
QueueDestroy(&q);
return 1; // 成功
}
// 二叉树的高度
int BinaryTreeHeight(BTNode* root) {
if (root == NULL) return 0;
int leftHeight = BinaryTreeHeight(root->left);
int rightHeight = BinaryTreeHeight(root->right);
return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
}
```
*** ** * ** ***
### test.c
```c
#include "BinaryTree.h"
// 测试手动构建和基本遍历
void TestBinaryTree1() {
printf("====== Test 1: 手动构建树 ======\n");
// 手动构建一个简单的树:
// 1
// / \
// 2 3
// / \
// 4 5
BTNode* n1 = BinaryTreeCreateNode(1);
BTNode* n2 = BinaryTreeCreateNode(2);
BTNode* n3 = BinaryTreeCreateNode(3);
BTNode* n4 = BinaryTreeCreateNode(4);
BTNode* n5 = BinaryTreeCreateNode(5);
n1->left = n2;
n1->right = n3;
n2->left = n4;
n2->right = n5;
printf("前序遍历: ");
PreOrder(n1); // 1 2 4 NULL NULL 5 NULL NULL 3 NULL NULL
printf("\n");
printf("中序遍历: ");
InOrder(n1);
printf("\n");
printf("后序遍历: ");
PostOrder(n1);
printf("\n");
printf("层序遍历: ");
LevelOrder(n1); // 1 2 3 4 5
printf("节点个数: %d\n", BinaryTreeSize(n1)); // 5
printf("叶子节点: %d\n", BinaryTreeLeafSize(n1)); // 3 (4, 5, 3)
printf("高度: %d\n", BinaryTreeHeight(n1)); // 3
printf("第3层节点数: %d\n", BinaryTreeLevelKSize(n1, 3)); // 2 (4, 5)
BTNode* find = BinaryTreeFind(n1, 5);
printf("查找值为5的节点: %p, 值: %d\n", find, find ? find->data : -1);
printf("是否完全二叉树? %s\n", BinaryTreeComplete(n1) ? "YES" : "NO"); // YES
BinaryTreeDestory(&n1);
printf("销毁后根节点指针: %p\n", n1);
}
// 测试数组构建和完全二叉树判断
void TestBinaryTree2() {
printf("\n====== Test 2: 数组构建与完全二叉树判断 ======\n");
// 构建一棵树: 1 2 3 # # # 4 5 # # 6 # #
// 注意:这里的 # 用 -1 表示
// 1
// / \
// 2 4
// / / \
// 3 5 6
int arr[] = { 1, 2, 3, -1, -1, -1, 4, 5, -1, -1, 6, -1, -1 };
int i = 0;
BTNode* root = BinaryTreeCreate(arr, sizeof(arr) / sizeof(arr[0]), &i);
printf("前序遍历检查: ");
PreOrder(root);
printf("\n");
printf("层序遍历: ");
LevelOrder(root);
// 这个结构不是完全二叉树,因为2号节点的右孩子为空,但4号节点存在
printf("是否完全二叉树? %s\n", BinaryTreeComplete(root) ? "YES" : "NO"); // Should be NO
printf("树的高度: %d\n", BinaryTreeHeight(root)); // 3
BinaryTreeDestory(&root);
}
int main() {
TestBinaryTree1();
TestBinaryTree2();
return 0;
}
```
*** ** * ** ***
## 🤔关于二叉树的在线OJ题
> [单值二叉树](https://leetcode.cn/problems/univalued-binary-tree/description/)
> [相同的树](https://leetcode.cn/problems/same-tree/description/)
> [对称二叉树](https://leetcode.cn/problems/symmetric-tree/description/)
> [二叉树的前序遍历](https://leetcode.cn/problems/binary-tree-preorder-traversal/description/)
> [二叉树的中序遍历](https://leetcode.cn/problems/binary-tree-inorder-traversal/description/)
> [二叉树的后序遍历](https://leetcode.cn/problems/binary-tree-postorder-traversal/description/)
> [另一棵树的子树](https://leetcode.cn/problems/subtree-of-another-tree/description/)
*** ** * ** ***
## 💻结尾--- 核心连接协议
**警告:** 🌠🌠正在接入底层技术矩阵。如果你已成功破解学习中的逻辑断层,请执行以下指令序列以同步数据:🌠🌠
*** ** * ** ***
**【📡】 建立深度链接:** **关注**本终端。在赛博丛林中深耕底层架构,从原始代码到进阶协议,同步见证每一次系统升级。
**【⚡】 能量过载分发:** 执行**点赞**操作。通过高带宽分发,让优质模组在信息流中高亮显示,赋予知识跨维度的传播力。
**【💾】 离线缓存核心:** 将本页加入**收藏**。把这些高频实战逻辑存入你的离线存储器,在遭遇系统崩溃或需要离线检索时,实现瞬时读取。
**【💬】 协议加密解密:** 在**评论区**留下你的散列码。分享你曾遭遇的代码冲突或系统漏洞(那些年踩过的坑),通过交互式编译共同绕过技术陷阱。
**【🛰️】 信号频率投票:** 通过**投票**发射你的选择。你的每一次点击都在重新定义矩阵的进化方向,决定下一个被全量拆解的技术节点。
*** ** * ** ***


