基于捷联惯导与多普勒计程仪组合导航的MATLAB算法实现

基于捷联惯导（SINS）与多普勒计程仪（DVL）组合导航的MATLAB算法实现方案

一、系统架构设计

1. 硬件组成

捷联惯导模块：三轴MEMS陀螺仪（零偏稳定性<0.1°/h）和加速度计（偏置稳定性<50μg）
多普勒计程仪：四波束Janus配置（测量精度±0.5% V）
主控单元：STM32H7+FPGA架构（实时数据处理）

2. 软件架构

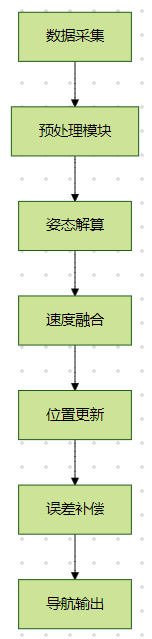
二、核心算法流程

1. 数据预处理

matlab 复制代码

% 多普勒测速数据预处理（MATLAB示例）
function [v_clean] = preprocess_dvl(raw_v, fs)
    % 巴特沃斯低通滤波（截止频率10Hz）
    [b,a] = butter(4, 10/(fs/2));
    v_filt = filter(b,a,raw_v);
    
    % 基线漂移补偿
    v_clean = v_filt - movmean(v_filt, 100);
end

2. 捷联惯导解算

matlab 复制代码

% 四元数姿态更新（四阶龙格-库塔法）
function q = update_attitude(gyro, dt)
    q = [1; 0; 0; 0]; % 初始四元数
    K1 = 0.5 * dt * gyro;
    K2 = 0.5 * dt * (gyro + 0.5 * K1);
    K3 = 0.5 * dt * (gyro + 0.5 * K2);
    K4 = 0.5 * dt * (gyro + K3);
    q = q + (K1 + 2*K2 + 2*K3 + K4)/6;
    q = q / norm(q); % 归一化
end

3. 组合导航滤波（UKF实现）

matlab 复制代码

% 无迹卡尔曼滤波核心代码
function [x_est, P] = unscented_kalman_filter(x, P, z, R, Q)
    % 状态维度
    n = length(x);
    % 生成Sigma点
    [X, W] = generate_sigma_points(x, P);
    
    % 传播过程
    X_pred = zeros(size(X));
    for i = 1:size(X,2)
        X_pred(:,i) = propagate_state(X(:,i), dt);
    end
    
    % 更新过程
    z_pred = measurement_model(X_pred);
    Pzz = cov(z_pred) + R;
    Pxz = cov(X_pred, z_pred);
    
    % 卡尔曼增益
    K = Pxz / Pzz;
    
    % 状态更新
    x_est = mean(X_pred) + K*(z - z_pred);
    P = P - K*Pzz*K';
end

function [X, W] = generate_sigma_points(x, P)
    n = length(x);
    lambda = 3 - n;
    X = zeros(n, 2*n+1);
    X(:,1) = x;
    P_sqrt = chol((n+lambda)*P);
    for i = 1:n
        X(:,i+1) = x + P_sqrt(:,i);
        X(:,i+2) = x - P_sqrt(:,i);
    end
    W = [lambda/(n+lambda), 0.5/(n+lambda)*ones(1,2n)];
end

三、关键算法实现

1. SINS/DVL数据融合

matlab 复制代码

function [state] = fuse_navigation(ins_data, dvl_data, dt)
    % 状态向量：[x, y, z, vx, vy, vz, wx, wy, wz]
    x = [ins_data.pos; ins_data.vel; ins_data.att];
    
    % 预测步骤
    F = compute_state_transition_matrix(x, dt);
    P = F * P_prior * F' + Q;
    
    % 更新步骤
    H = compute_measurement_matrix(x);
    K = P * H' / (H * P * H' + R_dvl);
    x = x + K * (dvl_data.vel - H * x);
    P = (eye(9) - K*H) * P;
    
    state = x;
end

function H = compute_measurement_matrix(x)
    % 观测矩阵（仅速度分量可观测）
    H = zeros(3,9);
    H(1,4) = 1; % x方向速度
    H(2,5) = 1; % y方向速度
    H(3,6) = 1; % z方向速度
end

2. DVL误差补偿模型

matlab 复制代码

% DVL误差补偿（基于文献的优化方法）
function v_comp = compensate_dvl_error(v_dvl, theta, dtheta, Ly, Lz)
    % 方程(9)的实现
    theta_avg = (theta + theta_delta)/2;
    delta_vx = (Ly * (dtheta) + Lz * (theta_avg)) / 2;
    delta_vy = (Lz * (dtheta) - Ly * (theta_avg)) / 2;
    v_comp = v_dvl - [delta_vx, delta_vy, 0];
end

四、完整仿真流程

初始化参数：

matlab 复制代码

fs = 100; % 采样频率(Hz)
dt = 1/fs; % 时间步长
T = 3600; % 仿真时长(秒)
N = T/dt; % 总步数

生成仿真数据：

matlab 复制代码

[true_traj, ins_data, dvl_data] = simulate_navigation(T, fs);

组合导航解算：

matlab 复制代码

state_est = zeros(9,N);
for k = 1:N
    [state_est(:,k)] = fuse_navigation(ins_data(:,k), dvl_data(:,k), dt);
end

误差分析：

matlab 复制代码

pos_error = sqrt(sum((true_traj - state_est(1:3,:)).^2,2));
plot(pos_error);
title('位置误差随时间变化');

五、实现建议

硬件加速 ：使用FPGA实现四元数运算加速（参考Xilinx FFT IP核） GPU并行计算（gpuArray加速矩阵运算）
实时性保障：采用双缓冲机制处理1kHz数据流任务调度优先级设置（高优先级：姿态解算）
容错设计： DVL失效时切换至纯INS模式（位置漂移补偿）冗余传感器交叉验证（如多DVL阵列）

六、扩展应用方向

深度学习辅助：

matlab 复制代码

% 基于LSTM的异常检测
layers = [ ...
    sequenceInputLayer(9)
    lstmLayer(20)
    fullyConnectedLayer(1)
    regressionLayer];
net = trainNetwork(XTrain,YTrain,layers);

多传感器融合：添加视觉SLAM（ORB-SLAM3算法）集成地磁传感器（姿态辅助）

七、参考

代码关于捷联惯导与多普勒计程仪组合导航的算法程序 www.youwenfan.com/contentcsp/98459.html
文献的DVL参数优化方法 www.ship-research.com/cn/article/pdf/preview/10.19693/j.issn.1673-3185.01934.pdf