【算法竞赛】链表和 list

🔭 个人主页：散峰而望

《C语言：从基础到进阶》《编程工具的下载和使用》《C语言刷题》《算法竞赛从入门到获奖》《人工智能》《AI Agent》
愿为出海月，不做归山云

🎬博主简介

【算法竞赛】链表和 list

前言
链表的概念
- [1.2 链表的分类](#1.2 链表的分类)
[2. 链表的模拟实现](#2. 链表的模拟实现)
- [2.1 单链表的模拟实现](#2.1 单链表的模拟实现)
- - [2.1.1 实现方式](#2.1.1 实现方式)
  - [2.1.2 定义 -- 创建 -- 初始化](#2.1.2 定义 -- 创建 -- 初始化)
  - [2.1.3 头插](#2.1.3 头插)
  - [2.1.4 任意位置后插入元素](#2.1.4 任意位置后插入元素)
  - [2.1.5 遍历链表](#2.1.5 遍历链表)
  - [2.1.6 按值查找](#2.1.6 按值查找)
  - [2.1.7 删除任意位置之后的元素](#2.1.7 删除任意位置之后的元素)
  - [2.1.8 遗留问题](#2.1.8 遗留问题)
- [2.2 双向链表的模拟实现](#2.2 双向链表的模拟实现)
- - [2.2.1 实现方式](#2.2.1 实现方式)
  - [2.2.3 头插](#2.2.3 头插)
  - [2.2.4 在任意位置之后插入元素](#2.2.4 在任意位置之后插入元素)
  - [2.2.5 在任意位置之前插入元素](#2.2.5 在任意位置之前插入元素)
  - [2.2.6 遍历链表](#2.2.6 遍历链表)
  - [2.2.7 按值查找](#2.2.7 按值查找)
  - [2.2.8 删除任意位置的元素](#2.2.8 删除任意位置的元素)
- [2.3 循环链表的模拟实现](#2.3 循环链表的模拟实现)
[3. 动态链表 -- list（了解）](#3. 动态链表 -- list（了解）)
- [3.1 创建 list](#3.1 创建 list)
- [3.2 push_front / push_back](#3.2 push_front / push_back)
- [pop_front / pop_back](#pop_front / pop_back)
结语

前言

链表是算法竞赛与数据结构中不可或缺的基础组件，其灵活的内存管理和高效的插入删除操作使其在特定场景下比数组更具优势。本文系统梳理了链表的核心概念、分类及实现方式，涵盖单链表、双向链表和循环链表的模拟实现细节，包括节点定义、初始化、插入删除操作及遍历查找等关键逻辑。同时对比动态链表（如 C++ STL中的 list 容器），分析其接口特性与实际应用场景。通过代码示例与问题思考，帮助读者深入理解链表的底层机制与性能权衡，为算法设计与优化奠定基础。

链表的概念

线性表的链式存储 就是链表。

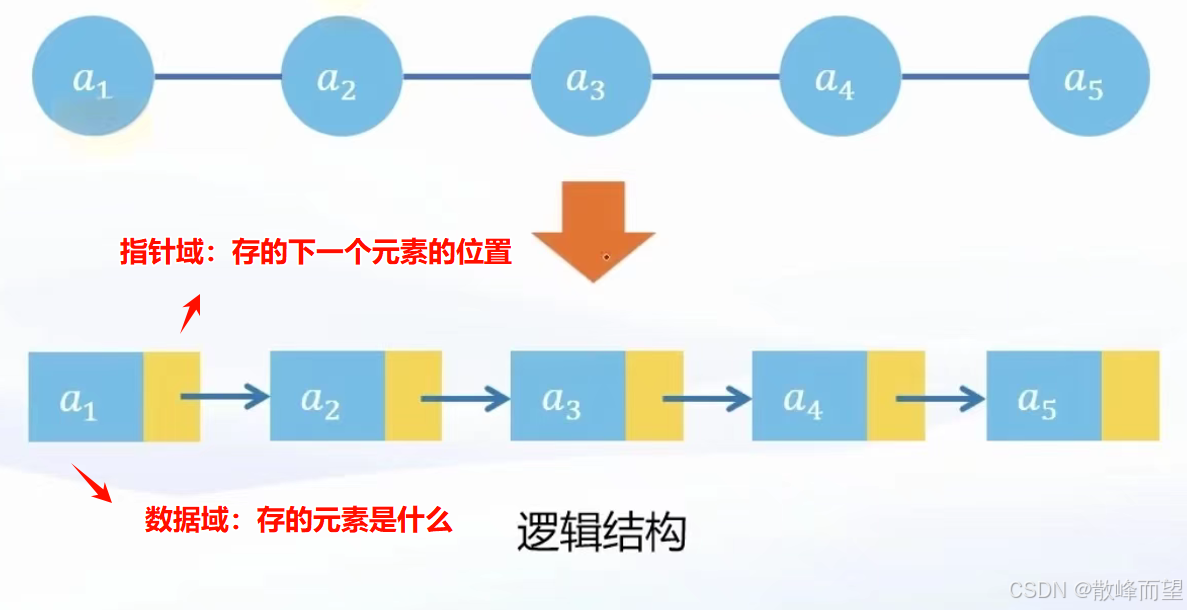
它是将元素存储在物理上任意的存储单元中，由于无法像顺序表一样通过下标保证数据元素之间的逻辑关系，链式存储除了要保存数据元素外，还需额外维护数据元素之间的逻辑关系，这两部分信息合称结点（node） 。即结点有两个域：保存数据元素的数据域 和存储逻辑关系的指针域。

结点： 即存储前继或后继的地址，通过地址实现元素与元素之间的关系。

1.2 链表的分类

将各种类型的链表排列组合，总共有 8 种不同的链表结构：

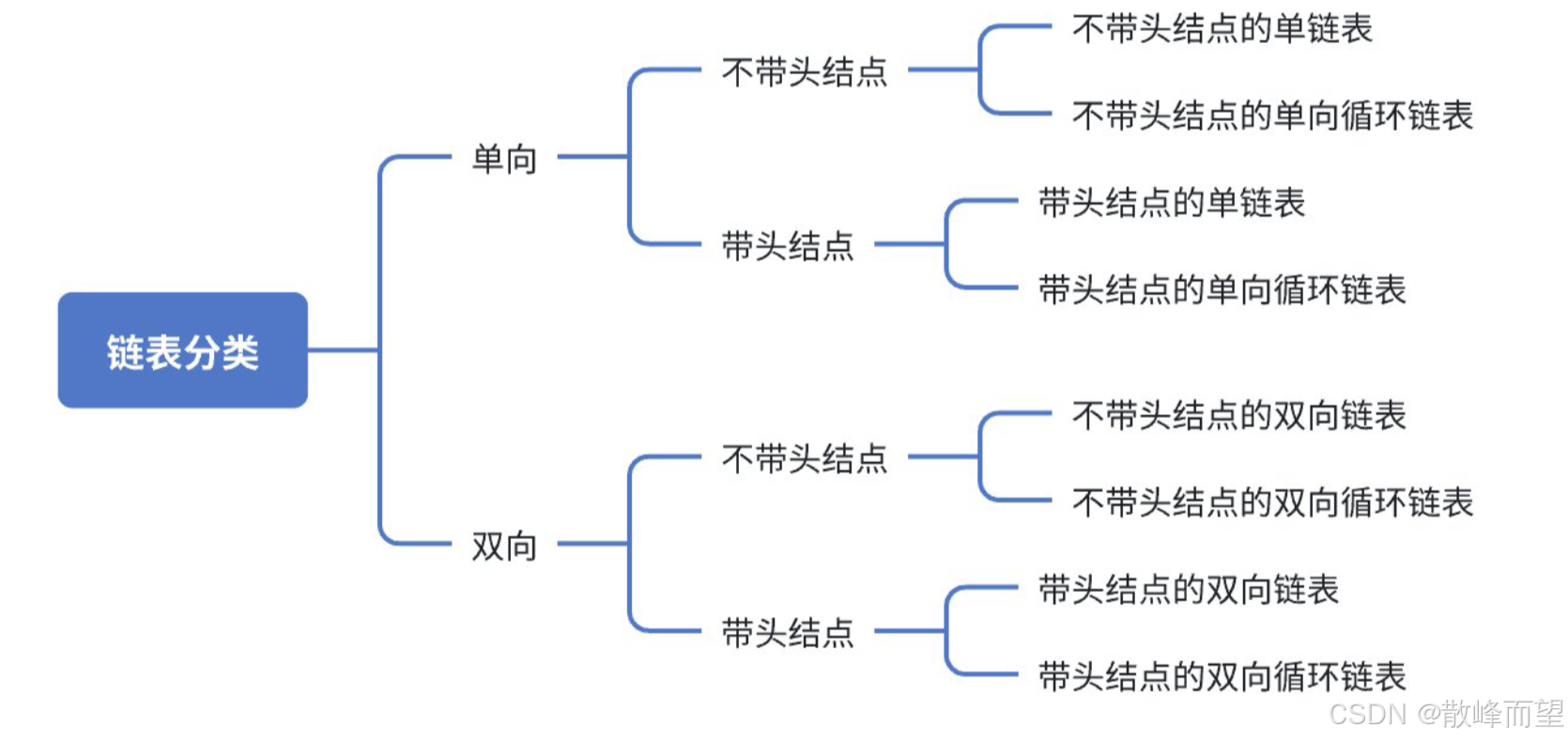
虽然链表种类较多，我们只需掌握单向链表 ，双向链表 和循环链表即可，熟悉之后其他链表便可自行实现。

2. 链表的模拟实现

2.1 单链表的模拟实现

2.1.1 实现方式

链表的实现方式分为动态实现 和静态实现两种。

动态实现是通过 new 申请结点，然后通过 delete 释放结点的形式构造链表。这种实现方式最能体现链表的特性，但频繁的调用 new 和 delete 会有很大的时间开销。
静态实现是利用两个数组配合来模拟链表。第一次接触可能比较抽象，但是它的运行速度很快，在算法竞赛中会经常会使用到。其中两个数组：一个存储数据，从当数据域 ；另一个存储下一个元素的下标，从当指针域 。同时还需要两个变量 ：一个标记头节点下标 ，另一个标记新来节点的存储位置。

2.1.2 定义 -- 创建 -- 初始化

两个足够大的数组，一个用来存数据，一个用来存下一个结点的位置

变量 h，充当头指针，表示头结点的位置

变量 id，为新来的结点分位置

逻辑结构：

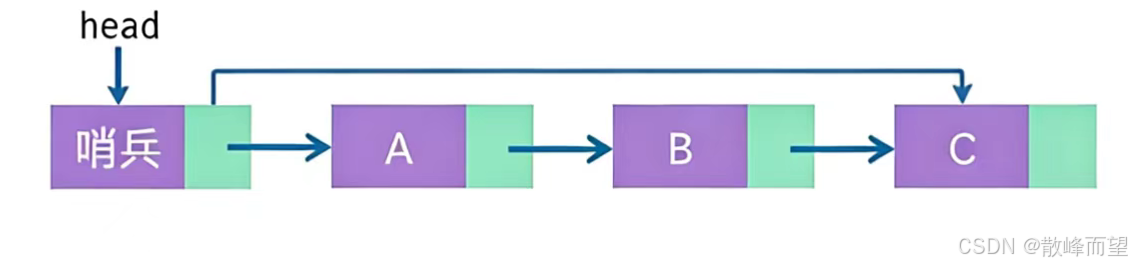
存储结构：

cpp 复制代码

#include <iostream>

const int N = 1e5 + 10;

int h; // 头指针 
int id; // 下一个元素分配的位置 
int e[N], ne[N]; // 数据域和指针域 
// 下标 0 位置作为哨兵位 
// 其中 ne 数组全部初始化为 0，其中 ne[i] = 0 就表示空指针，后续没有结点 
// 当然，也可以初始化为 -1 作为空指针，看个人爱好

e[i] 和 ne[i] 是绑定在一起使用的，也有一种写法是定义一个结构体，把这两个变量放在一起，比如：

cpp 复制代码

struct node
    {
        int e, ne;
    }list[N];

但是，定义成结构体之后，代码书写不方便。我们只要知道 e[i] 和 ne[i] 是绑定在一起使用的即可。

2.1.3 头插

这是链表中最常用也是使用最多的操作，后续树和图的存储中的邻接表以及链式前向星就会用到这个操作。
因此必须要掌握的操作。

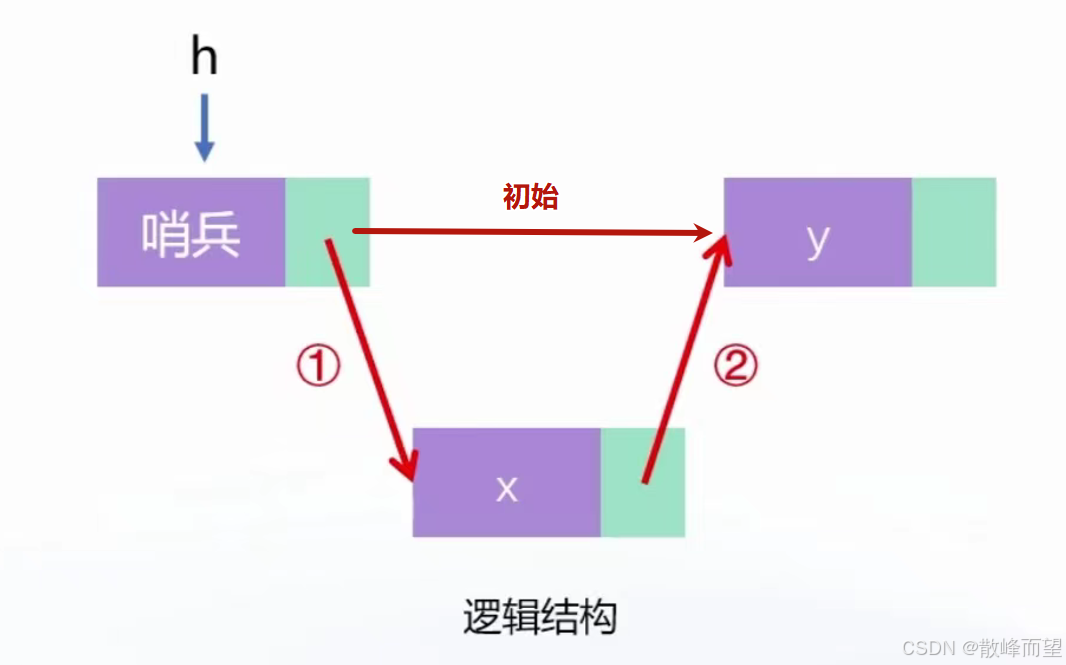
初始时，哨兵位的下一个位置指向 y 元素的下标位置，此时要插入一个 x 元素在头元素 y 前，现有两种修改指针的顺序，是先修改 ①→② 还是 ②→① 呢？

如果先修改 ①→②

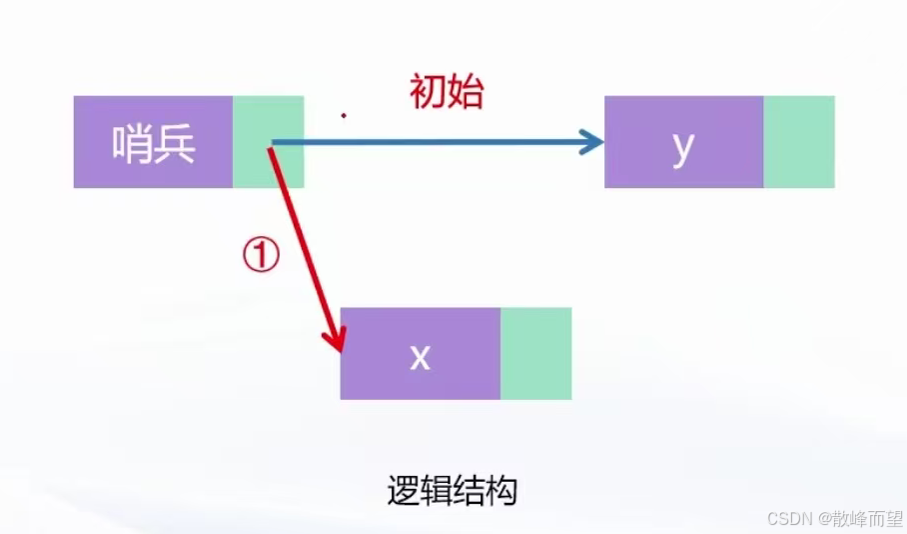
初始指针消失，以及所带后面的元素都找不到，再执行 ② 时，找不到下一个链表造成链表缺失。

如果先修改 ②→①

先 ② 的话可以找到下一个元素，并且 ② 对整个链表没有影响。

故先 ②→① 。

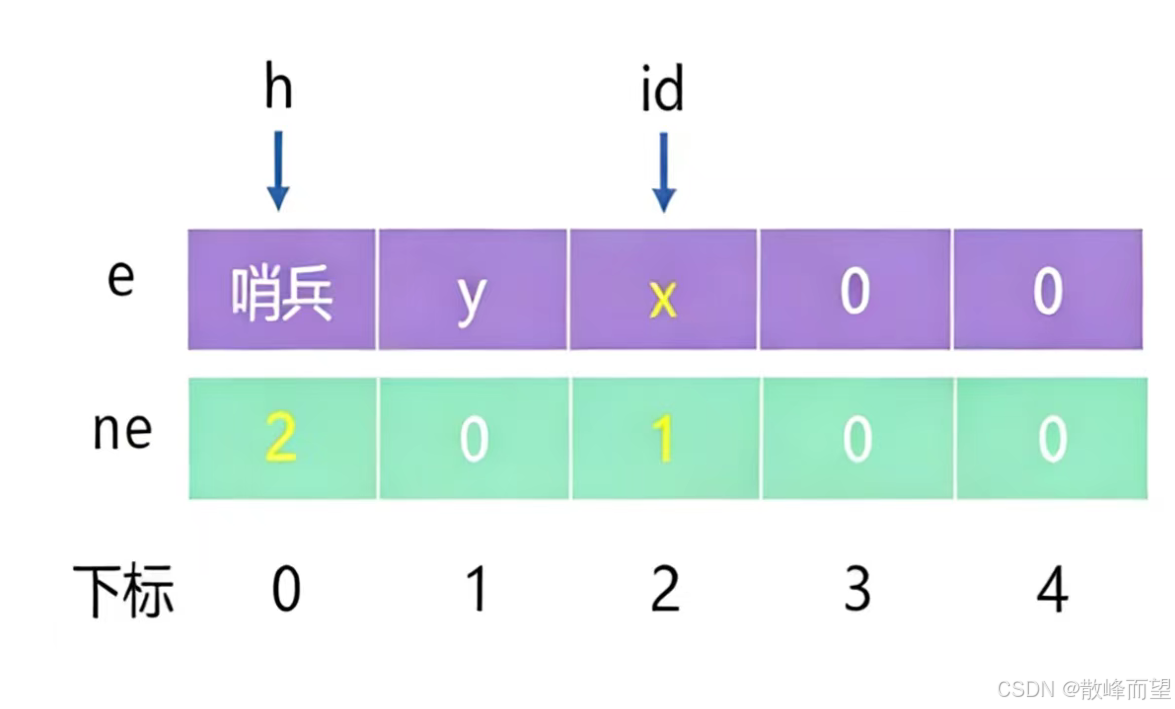
步骤：

先 id++; 使下标指向 y 后面的位置，标记新节点位置。同时存储新节点值：e[id] = x;
之后修改新节点指针域，让其指向哨兵位的下一个位置 ne[id] = ne[h]; 即指针 id 的 ne 数组里面存储的为 y 的下标
修改哨兵位的指针域，让其指向新节点 ne[h] = id;

cpp 复制代码

//头插
void push_front(int x)
{
	//先把x放在一个格子里面 
	id++;
	e[id] = x;
	
	//修改指针，顺序不能颠倒
	//1. x的右指针指向哨兵位的后继
	//2. 哨兵位的右指针指向x
	ne[id] = ne[h];
	ne[h] = id; 
 }

时间复杂度：

只涉及指针的修改，时间复杂度为 O(1)

2.1.4 任意位置后插入元素

任意位置后插会多传入存储位置 p ，这是因为传值也要找到其存储位置。

步骤：

先 id++; 使下标指向 y 后面的位置，标记新节点位置。同时存储新节点值：e[id] = x;
之后修改新节点指针域，让其指向哨兵位的下一个位置 ne[id] = ne[p]; 即指针 id 的 ne 数组里面存储的为 y 的下标
修改哨兵位的指针域，让其指向新节点 ne[p] = id;

和头插一样只是 ne[h] 改为 ne[p] 。

cpp 复制代码

//任意位置后插
void insert(int p, int x)//一定注意这里的p是位置，不是元素
{
	id++;
	e[id] = x;
	ne[id] = ne[p];
	ne[p] = id;
 }

时间复杂度：

只有常数级别的操作，时间复杂度为 O(1)

2.1.5 遍历链表

相当于指针从头结点开始，通过 ne 数组逐渐向后移动，直至遇到空指针。

cpp 复制代码

//遍历链表
void print()
{
	for(int i = ne[h]; i; i = ne[i])
	{
		cout << e[i] << " ";
	}
	cout << endl;
 }

时间复杂度：

遍历整个链表，时间复杂度为 O(N)

2.1.6 按值查找

查询链表中是否存在元素 x ，若存在，返回该元素下标。

法一：遍历整个链表即可

cpp 复制代码

//按值查找
int find(int x)
{
	for(int i = ne[h]; i; i = ne[i])
	{
		if(e[i] == x)
		{
			return i;
		}
	}
	//找不到就返回0
	return 0; 
 }

法二：如果存储的值数据范围不大，可以用哈希表优化（知道 mp 数组的作用就行，相当于一个标记数组，标记每个元素存储的下标）

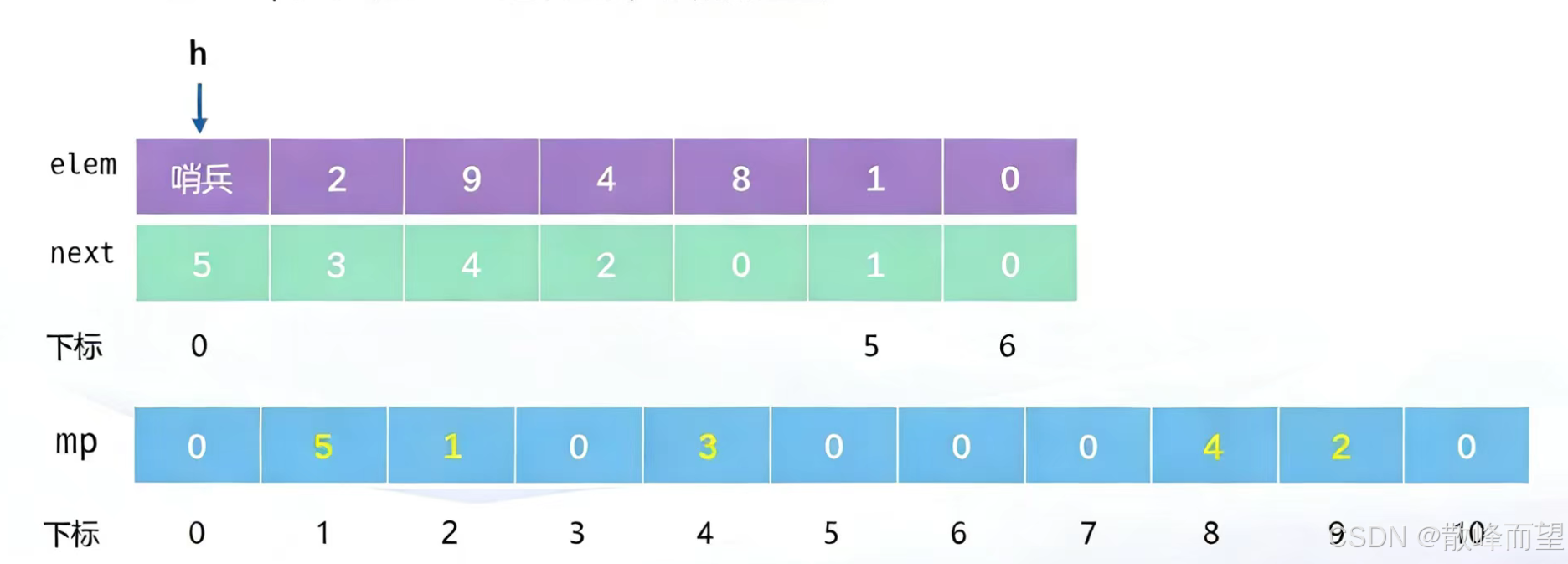
cpp 复制代码

//按值查找
int mp[i];// mp[i] 表示 i 在这个元素存放的位置 
/*
    push_front 和 insert 的时候，打上标记 
    mp[x] = id; // x 这个元素存放的位置是 id 
    
    erase 的时候，消除标记 
    mp[x] = 0;
*/
int find(int x)
{
	return mp[x];
 }

时间复杂度：

遍历整个链表查询：时间复杂度 O(N)

使用标记数组优化：时间复杂度 O(1)

2.1.7 删除任意位置之后的元素

删除 p 位置后面的元素

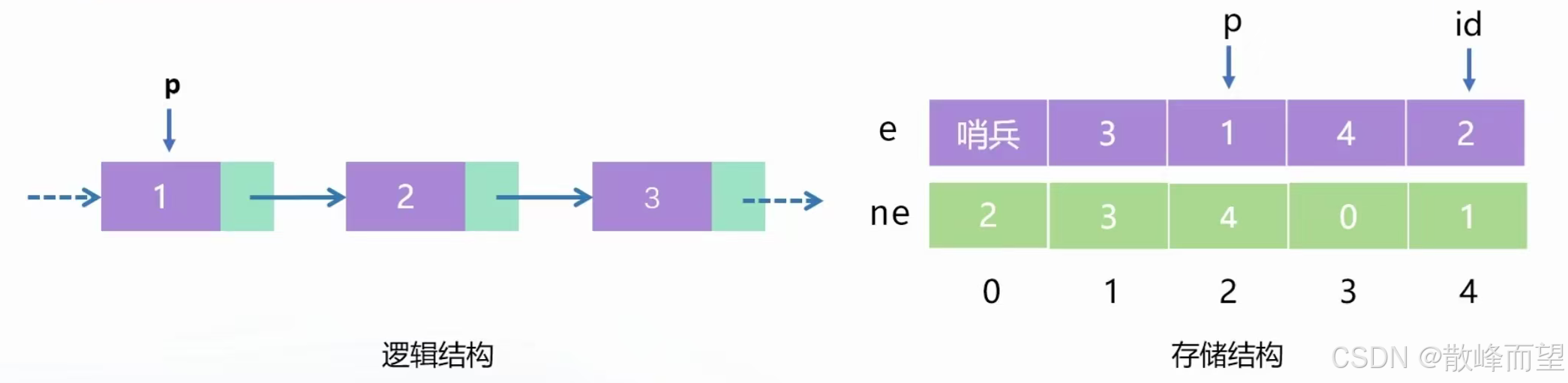
这里直接跳过 2 ，直接访问 3 即可：ne[p] = ne[ne[p]];，然后指向下一个元素的下一个元素。

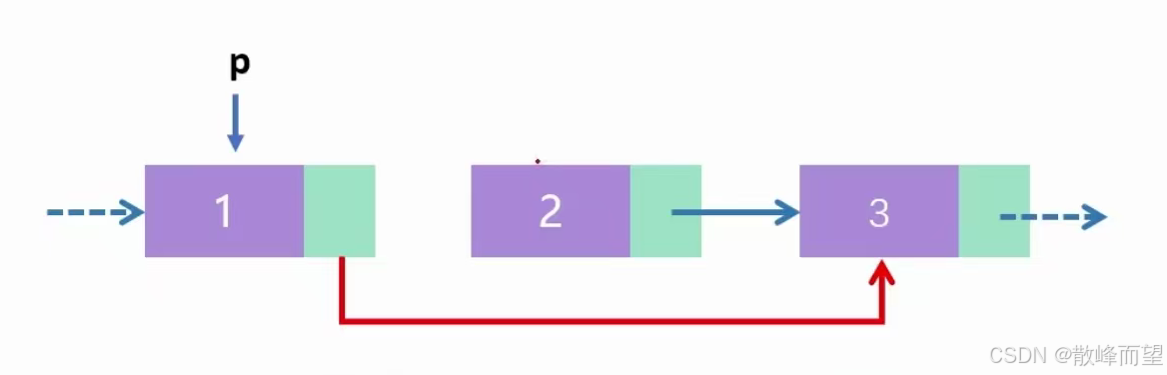
这里虽然没有删除 2 里面的元素，但是访问不到 2 ，相当于删除。

**注意：**这里有个 bug ，就是当删除的是最后一个元素时，会造成死循环，所以需要判断一下。

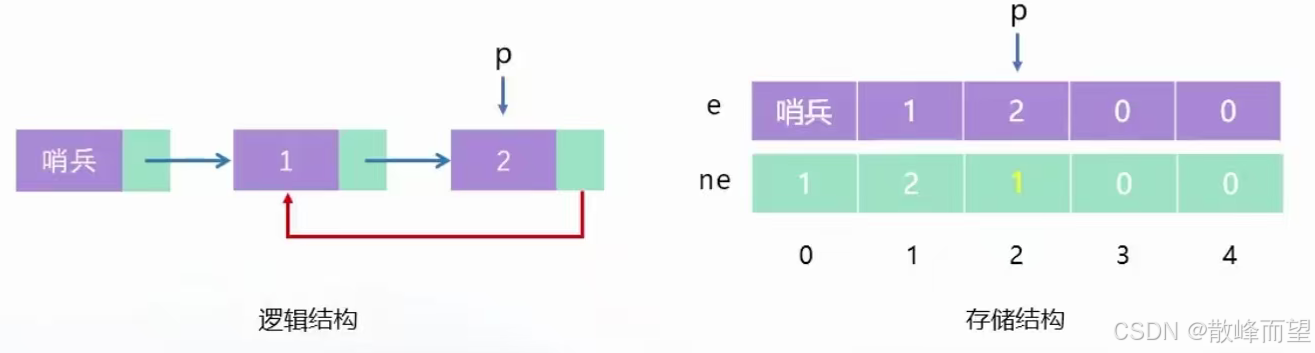
cpp 复制代码

// 删除存储位置为 p 后面的元素 
void erase(int p) // 注意 p 表示元素的位置 
{
    if(ne[p]) 
    {
        mp[e[ne[p]]] = 0; // 将 p 后面的元素从 mp 中删除 
        ne[p] = ne[ne[p]]; // 指向下一个元素的下一个元素 
    }
}

2.1.8 遗留问题

为什么不像顺序表一样，实现一个尾插、尾删、删除任意位置的元素等操作？

能实现，但是没必要。因为时间复杂度是 O(N) 。

尾插：有尾指针时 O(1) ，没有时需要遍历 O(N)
尾删：单向链表，尾指针不能往前，需遍历 O(N)
删除任意位置：删除后，需要修改前面 ne 指针，无法向前指，需遍历 O(N)

2.2 双向链表的模拟实现

2.2.1 实现方式

依旧采用静态实现的方式。

双向链表无非就是在单链表的基础上加上一个指向前驱的指针，那就再来一个数组，充当指向前驱的指针域即可。

cpp 复制代码

const int N = 1e5 + 10;
int h; // 头结点 
int id; // 下一个元素分配的位置 
int e[N]; // 数据域 
int pre[N], ne[N]; // 前后指针域 
// h 默认等于 0，指向的就是哨兵位 
// 此时链表为空，没有任何几点，因此 ne[h] = 0

2.2.3 头插

和单向链表一样，双向链表需要考虑其修改顺序

同时由单向链表可以推得只要 ① 指针最后修改即可。

则我们不妨这样操作：

先修改新节点 x 的左右指针 ② 和 ③
然后修改节点 y 的左指针 ④
最后修改哨兵位的右指针 ①

步骤：

先 id++; 使下标指向 y 后面的位置，标记新节点位置。同时存储新节点值：e[id] = x;
修改新节点的前驱指针，让其指向哨兵位 pre[id] = h;
修改新节点的后继指针，让其指向哨兵位下一个位置 ne[id] = ne[h];
修改 y 节点的前驱节点，让其指向新结点 pre[ne[h]] = id;
修改哨兵位的后继指针，让其指向新的节点 ne[h] =id;

cpp 复制代码

// 头插 
void push_front(int x)
{
    id++;
    e[id] = x;
    mp[x] = id; // 存一下 x 这个元素的位置 
    // 左指向哨兵位，右指向哨兵位的下一个位置，也就是头结点 
    pre[id] = h;
    ne[id] = ne[h];
     // 先修改头结点的指针，再修改哨兵位，顺序不能颠倒 
    pre[ne[h]] = id;
    ne[h] = id;
}

时间复杂度：

只涉及指针的修改，时间复杂度为 O(1)

2.2.4 在任意位置之后插入元素

基本步骤和头插类似，区别在于一个插入的是头节点 一个是元素 p 。

cpp 复制代码

// 在存储位置为 p 的元素后面，插入一个元素 x 
void insert_back(int p, int x)
{
    id++;
    e[id] = x;
    mp[x] = id; // 存一下 x 这个元素的位置 
    // 先左指向 p，右指向 p 的后继 
    pre[id] = p;
    ne[id] = ne[p];
    // 先让 p 的后继的左指针指向 id 
    // 再让 p 的右指针指向 id 
    pre[ne[p]] = id;
    ne[p] = id;
}

时间复杂度：

只涉及指针的修改，时间复杂度为 O(1)

2.2.5 在任意位置之前插入元素

与前两者插入不同在于：

之前插入把左指针 指向了 p 的前驱 ，右指针 指向 p

同时 p 的前驱的右指针 指向 id ，左指针 指向 id

cpp 复制代码

// 在存储位置为 p 的元素前面，插入一个元素 x
void insert_front(int p, int x)
{
    id++;
    e[id] = x;
    mp[x] = id; // 存一下 x 这个元素的位置 
    // 先左指针指向 p 的前驱，右指针指向 p 
    pre[id] = pre[p];
    ne[id] = p;
    // 先让 p 的前驱的右指针指向 id 
    // 再让 p 的左指针指向 id 
    ne[pre[p]] = id;
    pre[p] = id;
}

时间复杂度：

只涉及指针的修改，时间复杂度为 O(1)

2.2.6 遍历链表

和单链表的遍历方式一致。

cpp 复制代码

//遍历链表
void print()
{
	for(int i = ne[h]; i; i = ne[i])
	{
		cout << e[i] << " ";
	}
	cout << endl;
 }

时间复杂度：

遍历整个链表，时间复杂度为 O(N)

2.2.7 按值查找

直接使用 mp 数组。

cpp 复制代码

//按值查找
int mp[i];
int find(int x)
{
	return mp[x];
 }

时间复杂度：

使用标记数组优化：时间复杂度 O(1)

2.2.8 删除任意位置的元素

让 p 的前驱结点的后继指针指向 p 的后继结点
让 p 的后继节点的前驱指针指向 p 的前驱结点

cpp 复制代码

// 删除下标为 p 的元素 
void erase(int p)
{
    mp[e[p]] = 0; // 从标记中移除 
    ne[pre[p]] = ne[p];
    pre[ne[p]] = pre[p];
}

时间复杂度：

只涉及指针的修改，时间复杂度为 O(1)

2.3 循环链表的模拟实现

回看之前实现的带头单向链表。我们定义 0 表示空指针，但其实哨兵位就在 0 位置，所有的结构正好成环。

因此循环链表就是在原有的基础上，让最后一个元素指向表头即可，这里就不带着大家实现了。

3. 动态链表 -- list（了解）

new 和 delete 是非常耗时的操作，在算法比赛中，一般不会使用 new 和 delete 去模拟实现一个链表。

而 STL 里面的 list 的底层就是动态实现的双向循环链表，增删会涉及 new 和 delete，效率不高，竞赛中一般不会使用，这里了解一下即可。

3.1 创建 list

cpp 复制代码

#include <list>
using namespace std;
int main()
{
    list<int> lt; // 创建一个存储 int 类型的链表 
    return 0;
}

3.2 push_front / push_back

push_front：头插；
push_back：尾插。

时间复杂度：O(1)

cpp 复制代码

void testadd()
{
    list<int> lt;
    // 尾插 
    for(int i = 1; i <= 5; i++)
    {
        lt.push_back(i);
        print(lt);
    }
    
    
    // 头插 
    for(int i = 1; i <= 5; i++)
    {
        l.push_front(i);
        print(l);
    }
}

pop_front / pop_back

pop_front：头删
pop_back：尾删

时间复杂度：O(1)

cpp 复制代码

// 删 
void testdelete()
{
    list<int> lt;
     // 尾插 
    for(int i = 1; i <= 5; i++)
    {
        lt.push_back(i);
    }
    
    // 头插 
    for(int i = 5; i >= 1; i--)
    {
        lt.push_front(i);
    }
    // 头删 
    for(int i = 1; i <= 3; i++) lt.pop_front();
    // 尾删 
    for(int i = 1; i <= 3; i++) lt.pop_back();
    print(lt);
}

结语

链表作为数据结构的基础，在算法竞赛中具有重要地位。单链表、双向链表和循环链表的模拟实现展示了不同场景下的灵活性与效率差异，而动态链表（如 C++ 的 list）则提供了更便捷的容器化操作。

掌握链表的底层实现逻辑能够帮助优化代码性能，尤其在需要频繁插入、删除的场景中。同时，理解 list 的接口特性（如 push_front、pop_back）可以快速解决实际问题。

无论是手动实现链表还是使用标准库，核心在于根据需求选择合适的数据结构，平衡时间复杂度和空间复杂度。通过实践与总结，链表将成为算法工具箱中的利器。

愿诸君能一起共渡重重浪，终见缛彩遥分地，繁光远缀天。