pytorch深度学习笔记15

目录

摘要

1.Momentum

2.学习率衰减

​​​​​​​等间隔衰减

​​​​​​​指定间隔衰减

​​​​​​​指数衰减

---

摘要

本篇文章继续学习尚硅谷深度学习教程，学习内容是动量法和学习率衰减

1.Momentum

原始的梯度下降法直接使用当前梯度来更新参数：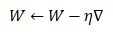

而Momentum（动量法）会保存历史梯度并给予一定的权重，使其也参与到参数更新中：

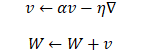
• ：历史（负）梯度的加权和
• ：历史梯度的权重
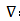• ：当前梯度，即
• ：学习率

动量法有时能够减缓优化过程中的震荡，加快优化的速度。因为其会累计历史梯度，也可以有效避免鞍点问题。

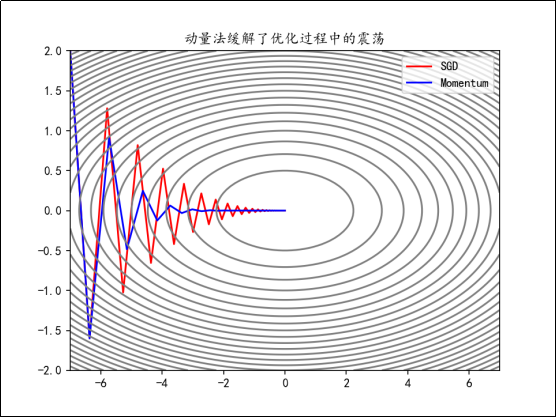
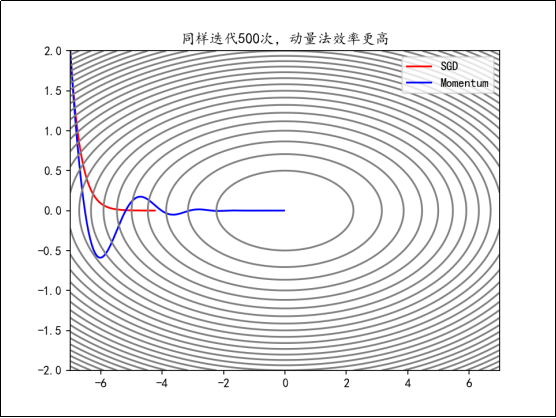
Momentum的代码实现如下：

class Momentum:

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():                                
                self.v[key] = np.zeros_like(val)
                
        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] 
            params[key] += self.v[key]

2.​​​​​​​学习率衰减

深度学习模型训练中调整最频繁的当属学习率，好的学习率可以使模型逐渐收敛并获得更好的精度。较大的学习率可以加快收敛速度，但可能在最优解附近震荡或不收敛；较小的学习率可以提高收敛的精度，但训练速度慢。学习率衰减是一种平衡策略，初期使用较大学习率快速接近最优解，后期逐渐减小学习率，使参数更稳定地收敛到最优解。

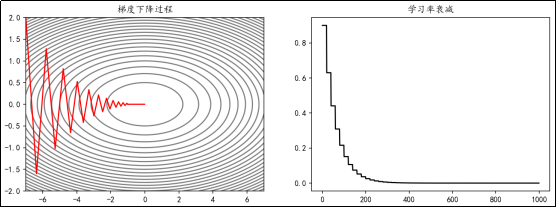
​​​​​​​等间隔衰减

每隔固定的训练周期（epoch），学习率按一定的比例下降，也称为"步长衰减"。例如，使学习率每隔20 epoch衰减为之前的0.7：

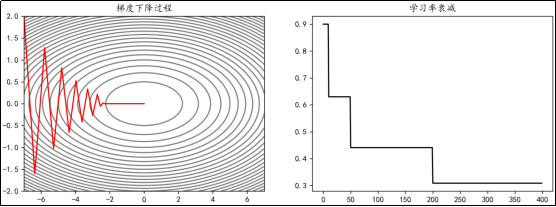
​​​​​​​指定间隔衰减

在指定的epoch，让学习率按照一定的系数衰减。例如，使学习率在epoch达到10,50,200时衰减为之前的0.7：

​​​​​​​指数衰减

学习率按照指数函数进行衰减。例如，使学习率以0.99为底数，epoch为指数衰减：