做线性回归的过程如图1所示。图中的实线框表示必不可少的步骤,虚线框表示可选的步骤。
首先要准备数据。通常准备数据先是要加载数据。数据的来源可以是文本文件、Excel文件、各种数据库。
要想打好机器学习的数学基础,请参见清华大学出版社的人人可懂系列,包括《人人可懂的微积分》(已上市)、《人人可懂的线性代数》(即将上市)、《人人可懂的概率统计》(即将上市)。
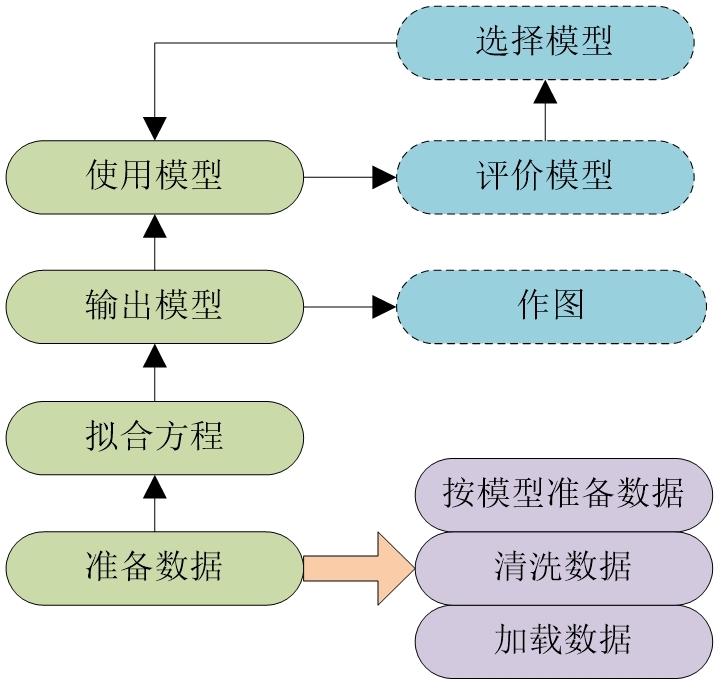
图1 做线性回归的过程
加载完数据后,通常会要对数据进行清洗。可以在加载之前就清洗好数据,也可以在加载之后用Python程序清洗。常见的清洗工作包括去掉有缺失项的数据或对有缺失的数据用一定的算法做填充、将文本置换成数字表示、将数据置换成特定的特征值等。
还要按模型建模的需要来准备数据。后续我们还会讲解这样的实例。
准备好数据后,就要拟合方程了。线性回归的做法是假定已知数据的关系会呈线性,给定一个特定的线性方程,再求解这个线性方程的系数、截距。
**提示:**提醒大家要特别注意的是:机器学习模型求解的不是x ,而是模型中的参数,线性回归里这些参数就是 θ 0 ... θ n \theta_{0}\ldots\theta_{n} θ0...θn。这一点一定要理解,由于数学中常用x 表示未知量,初学者很容易混淆。这里要把x 看成已知的量来求解未知参数 θ 0 ... θ n \theta_{0}\ldots\theta_{n} θ0...θn。
求解模型后可以将模型保存起来备用、也可以输出模型的效果图。最为直观的方法自然是作图。只是三维及三维以下的图形还可以图示,三维以上的图形就不能图示了。不过,还可以对数据作降维处理后降到三维就可以图示了。
要想打好机器学习的数学基础,请参见清华大学出版社的人人可懂系列,包括《人人可懂的微积分》(已上市)、《人人可懂的线性代数》(即将上市)、《人人可懂的概率统计》(即将上市)。
使用模型主要就是用模型来做预测,即根据新输入的特征数据项使用模型来预测目标数据项的值。如果有多个模型则可作模型的比较来从中选取最佳的模型来做预测。根据什么评价指标来比较呢?有很多种评价指标可以选用。