leetcode 174 地下城游戏

小欣加油2026-01-15 13:39

一、问题描述

二、解题思路

整体思路

本题属于路径相关问题的变形，可以采用动态规划的方法来解决这个问题。

具体思路

(1)dp $i$ $j$ 含义

由于本题是具有后滞性的动态规划问题，所以不同于一般路径问题dp $i$ $j$ 表示以(i，j)为终点，本题的dp $i$ $j$ 表示以(i，j)为起点的最小生命值。

(2)状态转移方程

设当前的生命值为x，则有x+d $i$ $j$ >= dp $i+1$ $j$ ，即x>=dp $i+1$ $j$ -d $i$ $j$ ，最小生命值为dp $i+1$ $j$ -d $i$ $j$ ，向下亦然，所以dp $i$ $j$ =min(dp $i+1$ $j$ ,dp $i$ $j+1$ )-d $i$ $j$ 。

注意：由于生命值<=0表示死亡，所以计算后需要执行dp $i$ $j$ =max(1,dp $i$ $j$ )。

(3)初始化

dp数组为(m+1)*(n+1)的数组，先将所有位置初始化为正无穷，(m-1,n)和(m,n-1)位置初始化为1，为了计算dp $m-1$ $n-1$ 的值，以示例一为例，初始化后的数组为：

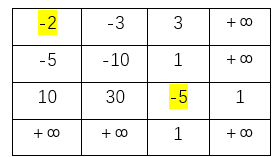
(4)填表顺序

从后往前，从右向左进行填写。

(5)返回值

dp $0$ $0$ 即为所求，返回即可。

三、代码实现

cpp 复制代码

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& d) {
        //有后效性的动态规划
        int m = d.size();
        int n = d[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));
        dp[m][n-1] = dp[m-1][n] = 1;

        //从后向前,从右向左，填写dp数组
        for(int row = m-1;row >=0;row--)
            for(int col = n-1;col >=0;col--){
                dp[row][col] = min(dp[row+1][col],dp[row][col+1])-d[row][col];
                dp[row][col] = max(1,dp[row][col]);
            }
        //返回值
        return dp[0][0];
    }
};