第 3 章 灰度变换与空间域滤波

啊阿狸不会拉杆2026-01-18 18:20

前言

大家好！今天给大家分享《数字图像处理》中最核心的章节之一 ------ 灰度变换与空间域滤波。这一章是图像增强的基础，不管是图像的对比度调整、去噪还是锐化，都离不开这些核心技术。本文会结合完整可运行的 Python 代码，对每个知识点进行通俗易懂的讲解，并通过效果对比图直观展示处理效果，方便大家动手实践。

3.1 背景知识

3.1.1 灰度变换与空间域滤波的基本原理

  • 灰度变换 ：直接对图像的每个像素灰度值进行数学变换，改变像素的灰度范围或分布，核心是s = T(r)（r 为原始灰度，s 为变换后灰度，T 为变换函数）。
  • 空间域滤波：基于像素的邻域（空间位置）进行操作，通过卷积 / 相关运算，用滤波模板（核）对像素邻域加权求和，实现去噪、锐化等效果。

3.1.2 本章示例说明

本文所有示例均基于 Python 实现，依赖库包括：numpy（数值计算）、cv2（图像读取 / 处理）、matplotlib（可视化）、skimage（直方图处理辅助）。环境准备：

复制代码 
pip install numpy opencv-python matplotlib scikit-image

3.2 常用灰度变换函数

3.2.1 图像求反

原理：对灰度值取反，公式：

完整代码：

复制代码 
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体，避免乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 读取图像（灰度模式）
img = cv2.imread('test_img.jpg', cv2.IMREAD_GRAYSCALE)
if img is None:
    raise ValueError("请确保test_img.jpg文件存在于当前目录！")

# 3.2.1 图像求反
def image_negation(img):
    """图像求反"""
    L = 256  # 8位图像灰度级
    neg_img = L - 1 - img
    return neg_img

# 计算求反图像
neg_img = image_negation(img)

# 可视化对比
plt.figure(figsize=(12, 6))
# 原始图像
plt.subplot(1, 2, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')
# 求反图像
plt.subplot(1, 2, 2)
plt.imshow(neg_img, cmap='gray')
plt.title('图像求反结果')
plt.axis('off')

plt.show()

3.2.2 对数变换

原理：压缩高灰度值范围，扩展低灰度值范围，公式：

完整代码：

python 复制代码 
import matplotlib.pyplot as plt
import cv2
import numpy as np

# 设置中文字体，避免乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 3.2.2 对数变换
def log_transform(img):
    """对数变换"""
    # 归一化到[0,1]，避免数值溢出
    img_normalized = img / 255.0
    # 计算对数变换，c=1（可调整）
    log_img = np.log(1 + img_normalized)
    # 归一化回[0,255]
    log_img = (log_img / np.max(log_img)) * 255
    log_img = log_img.astype(np.uint8)
    return log_img

# 读取图像
img = cv2.imread('../picture/Mei.png', cv2.IMREAD_GRAYSCALE)
if img is None:
    raise ValueError("请确保test_img.jpg文件存在于当前目录！")
# 计算对数变换图像
log_img = log_transform(img)

# 可视化对比
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

plt.subplot(1, 2, 2)
plt.imshow(log_img, cmap='gray')
plt.title('对数变换结果')
plt.axis('off')

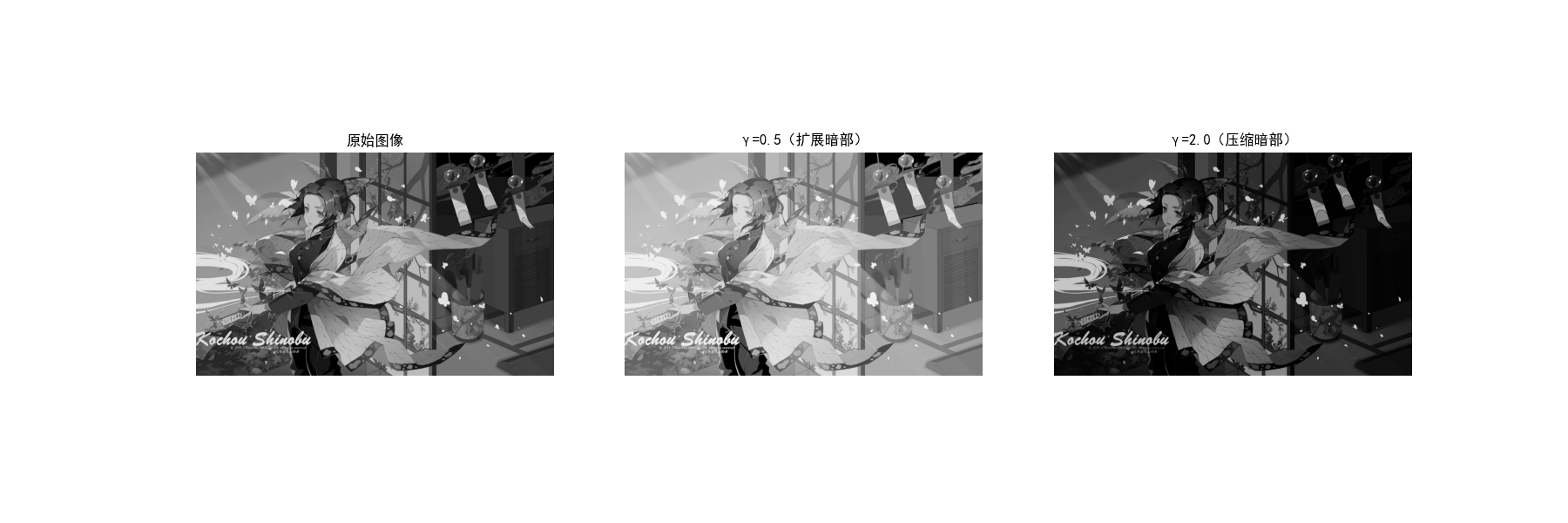
plt.show()

3.2.3 幂律（伽马）变换

原理：通过调整伽马值（γ）控制灰度变换趋势，公式：

  • γ>1：压缩低灰度，扩展高灰度；
  • γ<1：扩展低灰度，压缩高灰度；
  • γ=1：无变换。

完整代码：

python 复制代码 
import matplotlib.pyplot as plt
import cv2
import numpy as np

# 设置中文字体，避免乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 3.2.3 伽马变换
def gamma_transform(img, gamma=1.0):
    """伽马变换"""
    # 归一化到[0,1]
    img_normalized = img / 255.0
    # 伽马变换（避免0的幂次问题，加小epsilon）
    gamma_img = np.power(img_normalized + 1e-8, gamma)
    # 归一化回[0,255]
    gamma_img = (gamma_img / np.max(gamma_img)) * 255
    gamma_img = gamma_img.astype(np.uint8)
    return gamma_img
# 读取图像
img = cv2.imread('../picture/Ren.png', cv2.IMREAD_GRAYSCALE)
if img is None:
    raise ValueError("请确保test_img.jpg文件存在于当前目录！")
# 测试不同伽马值
gamma_0_5 = gamma_transform(img, gamma=0.5)  # 扩展暗部
gamma_2_0 = gamma_transform(img, gamma=2.0)  # 压缩暗部

# 可视化对比
plt.figure(figsize=(18, 6))
plt.subplot(1, 3, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

plt.subplot(1, 3, 2)
plt.imshow(gamma_0_5, cmap='gray')
plt.title('γ=0.5（扩展暗部）')
plt.axis('off')

plt.subplot(1, 3, 3)
plt.imshow(gamma_2_0, cmap='gray')
plt.title('γ=2.0（压缩暗部）')
plt.axis('off')

plt.show()

3.2.4 分段线性变换函数

原理：分区间定义线性变换，常用于增强特定灰度范围的对比度（如拉伸感兴趣的灰度区间）。

示例：拉伸灰度区间 [50, 150] 到 [0, 255]，其余区间压缩。

完整代码：

python 复制代码 
import matplotlib.pyplot as plt
import cv2
import numpy as np

# 设置中文字体，避免乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 3.2.4 分段线性变换
def piecewise_linear_transform(img):
    """分段线性变换：拉伸[50,150]区间"""
    # 创建变换后的图像
    piece_img = np.zeros_like(img, dtype=np.float32)
    # 分段函数
    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
            r = img[i, j]
            if r < 50:
                s = 0.5 * r  # 压缩低灰度
            elif 50 <= r <= 150:
                s = 2.55 * (r - 50)  # 拉伸中间灰度
            else:
                s = 200 + 0.55 * (r - 150)  # 压缩高灰度
            piece_img[i, j] = s
    # 裁剪到[0,255]并转换类型
    piece_img = np.clip(piece_img, 0, 255).astype(np.uint8)
    return piece_img

# 读取图像
img = cv2.imread('../picture/AALi.jpg', cv2.IMREAD_GRAYSCALE)
if img is None:
    raise ValueError("请确保test_img.jpg文件存在于当前目录！")
# 计算分段线性变换图像
piece_img = piecewise_linear_transform(img)

# 可视化对比
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

plt.subplot(1, 2, 2)
plt.imshow(piece_img, cmap='gray')
plt.title('分段线性变换结果')
plt.axis('off')

plt.show()

3.3 直方图处理

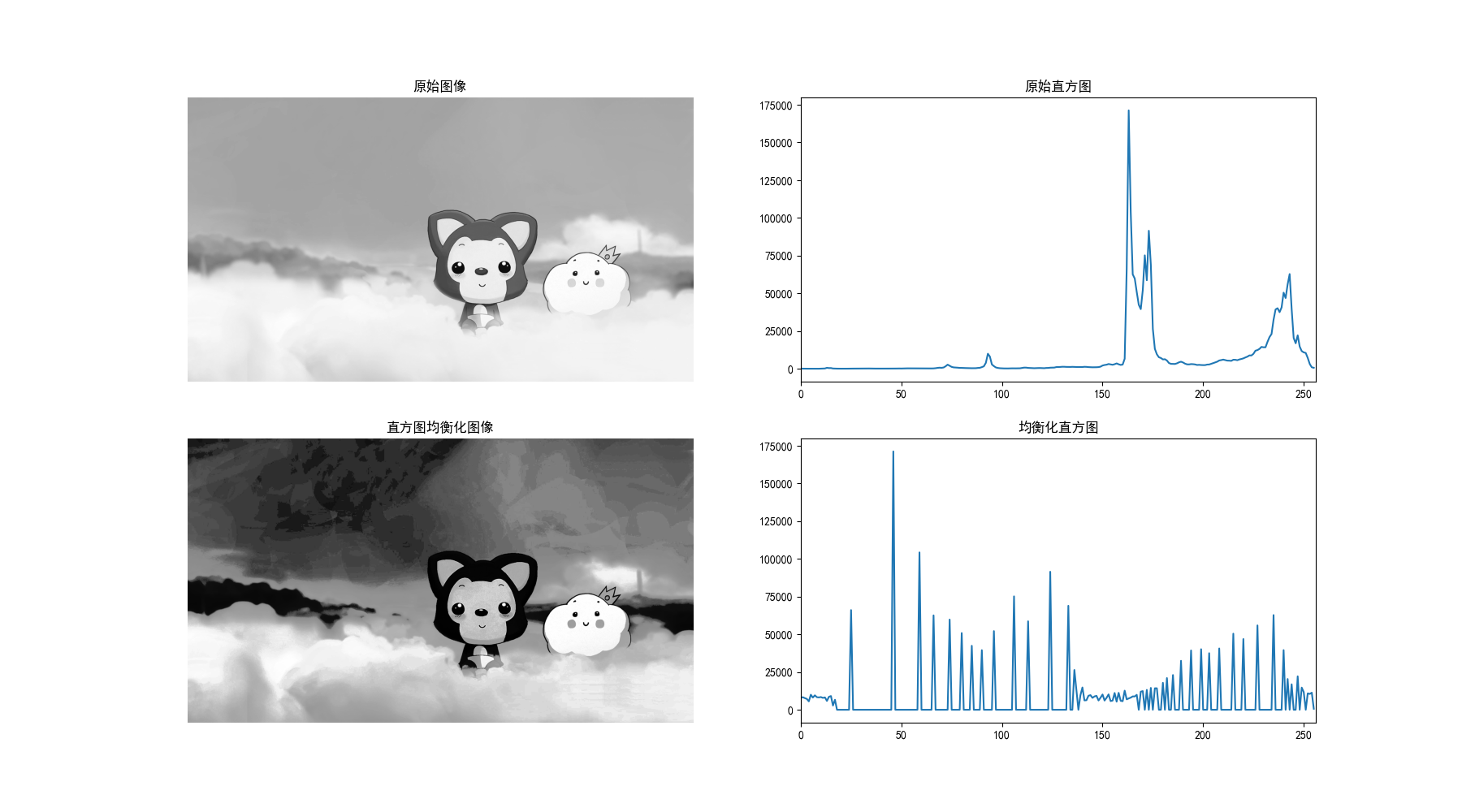
3.3.1 直方图均衡化

原理：将图像的直方图均匀分布，提升整体对比度，公式：

完整代码：

python 复制代码 
import matplotlib.pyplot as plt
import cv2
import numpy as np

# 设置中文字体，避免乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
from skimage import exposure

# 3.3.1 直方图均衡化
def histogram_equalization(img):
    """直方图均衡化"""
    # 手动实现（也可直接用cv2.equalizeHist）
    # 1. 计算直方图
    hist, bins = np.histogram(img.flatten(), 256, [0, 256])
    # 2. 计算累积分布函数(CDF)
    cdf = hist.cumsum()
    # 3. 归一化CDF
    cdf_normalized = cdf / cdf.max()
    # 4. 映射灰度值
    eq_img = np.interp(img.flatten(), bins[:-1], cdf_normalized * 255)
    eq_img = eq_img.reshape(img.shape).astype(np.uint8)
    return eq_img, hist, cdf
# 读取图像
img = cv2.imread('../picture/ALi.jpg', cv2.IMREAD_GRAYSCALE)
if img is None:
    raise ValueError("请确保test_img.jpg文件存在于当前目录！")
# 计算均衡化图像及直方图
eq_img, hist_original, cdf_original = histogram_equalization(img)
# 计算均衡化后的直方图
hist_eq, _ = np.histogram(eq_img.flatten(), 256, [0, 256])

# 可视化对比（图像+直方图）
plt.figure(figsize=(18, 10))
# 原始图像
plt.subplot(2, 2, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')
# 原始直方图
plt.subplot(2, 2, 2)
plt.plot(hist_original)
plt.title('原始直方图')
plt.xlim([0, 256])
# 均衡化图像
plt.subplot(2, 2, 3)
plt.imshow(eq_img, cmap='gray')
plt.title('直方图均衡化图像')
plt.axis('off')
# 均衡化直方图
plt.subplot(2, 2, 4)
plt.plot(hist_eq)
plt.title('均衡化直方图')
plt.xlim([0, 256])

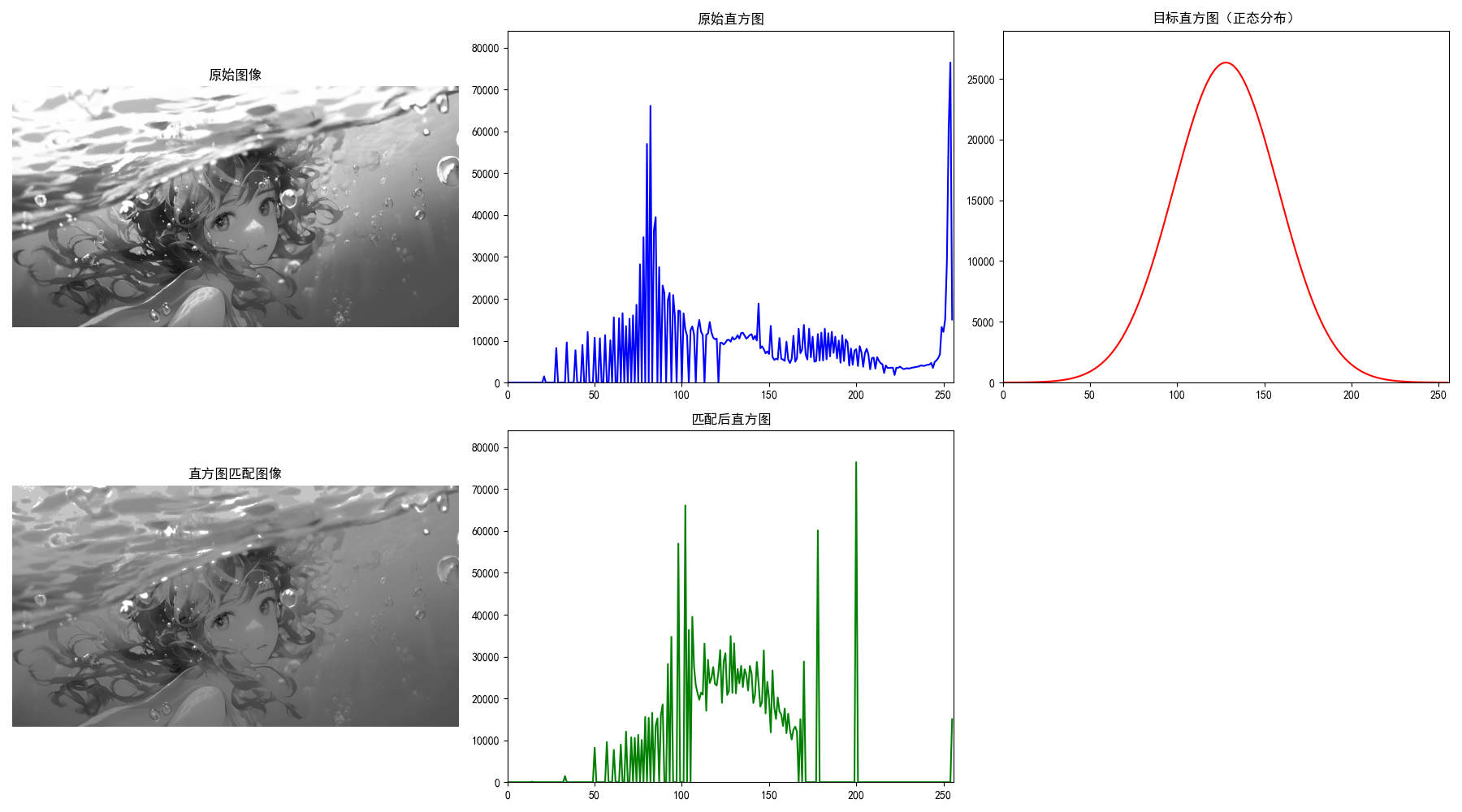
plt.show()

3.3.2 直方图匹配（规定化）

原理：将原始图像的直方图匹配到目标直方图（如正态分布、另一幅图像的直方图），实现可控的对比度调整。

完整代码：

python 复制代码 
import matplotlib.pyplot as plt
import cv2
import numpy as np

# 设置中文字体，避免乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 3.3.2 直方图匹配
def histogram_matching(img, target_hist):
    """
    直方图匹配
    img: 原始图像
    target_hist: 目标直方图（长度256）
    返回值:
        match_img: 匹配后的图像
        hist_original: 原始图像直方图
    """
    # 1. 原始图像的CDF
    hist_original, _ = np.histogram(img.flatten(), 256, [0, 256])
    cdf_original = hist_original.cumsum() / hist_original.sum()

    # 2. 目标直方图的CDF
    cdf_target = target_hist.cumsum() / target_hist.sum()

    # 3. 建立灰度映射表
    mapping = np.zeros(256, dtype=np.uint8)
    for i in range(256):
        # 找到最接近的CDF值
        diff = np.abs(cdf_original[i] - cdf_target)
        mapping[i] = np.argmin(diff)

    # 4. 应用映射
    match_img = mapping[img]
    return match_img, hist_original  # 新增返回原始直方图

# 读取图像（请确认路径正确）
img = cv2.imread('../picture/Water.png', cv2.IMREAD_GRAYSCALE)
if img is None:
    # 友好提示：检查路径和文件名，同时给出备选方案
    raise ValueError(
        "图像读取失败！请检查：\n"
        "1. 文件路径 '../picture/ALi.jpg' 是否正确\n"
        "2. 文件是否存在且为有效图像格式（jpg/png等）\n"
        "3. 替换为你的实际图像路径后重试"
    )

# 生成目标直方图（正态分布）
x = np.linspace(0, 255, 256)
target_hist = np.exp(-((x - 128) ** 2) / (2 * 30 ** 2))  # 均值128，方差30
target_hist = (target_hist / target_hist.sum()) * img.size  # 归一化到总像素数

# 计算匹配图像（同时接收返回的原始直方图）
match_img, hist_original = histogram_matching(img, target_hist)

# 计算匹配后的直方图
hist_match, _ = np.histogram(match_img.flatten(), 256, [0, 256])

# 可视化对比
plt.figure(figsize=(18, 10))
# 第一行：原始图像、原始直方图、目标直方图
plt.subplot(2, 3, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

plt.subplot(2, 3, 2)
plt.plot(hist_original, color='blue')
plt.title('原始直方图')
plt.xlim([0, 256])
plt.ylim([0, max(hist_original) * 1.1])  # 优化y轴范围，显示更美观

plt.subplot(2, 3, 3)
plt.plot(target_hist, color='red')
plt.title('目标直方图（正态分布）')
plt.xlim([0, 256])
plt.ylim([0, max(target_hist) * 1.1])

# 第二行：匹配后图像、匹配后直方图、空白（保持布局对称）
plt.subplot(2, 3, 4)
plt.imshow(match_img, cmap='gray')
plt.title('直方图匹配图像')
plt.axis('off')

plt.subplot(2, 3, 5)
plt.plot(hist_match, color='green')
plt.title('匹配后直方图')
plt.xlim([0, 256])
plt.ylim([0, max(hist_match) * 1.1])

# 隐藏第六个子图，保持布局整洁
plt.subplot(2, 3, 6)
plt.axis('off')

plt.tight_layout()  # 自动调整子图间距，避免标题重叠
plt.show()

3.3.3 局部直方图处理

原理：对图像的每个像素，基于其邻域（如 3x3、5x5）计算直方图均衡化，增强局部细节（如纹理、边缘）。

完整代码：

python 复制代码 
import matplotlib.pyplot as plt
import cv2
import numpy as np
from skimage import exposure

# 设置中文字体，避免乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


# 3.3.3 局部直方图均衡化
def local_histogram_equalization(img, block_size=15):
    """
    局部直方图均衡化（自适应直方图均衡化）
    参数:
        img: 输入灰度图像（numpy数组）
        block_size: 邻域大小（奇数，建议为3-31之间的奇数）
    返回:
        local_eq_img: 局部均衡化后的图像
    异常处理:
        校验block_size为奇数，避免skimage函数报错
    """
    # 校验block_size为奇数（equalize_adapthist要求kernel_size为奇数）
    if block_size % 2 == 0:
        block_size += 1  # 自动转为奇数
        print(f"提示：block_size需为奇数，已自动调整为 {block_size}")

    # 使用skimage的自适应直方图均衡化函数
    local_eq_img = exposure.equalize_adapthist(img, kernel_size=block_size)
    # 归一化到[0,255]并转换为8位无符号整数
    local_eq_img = (local_eq_img * 255).astype(np.uint8)
    return local_eq_img


# 读取图像（请确认路径正确）
img = cv2.imread('../picture/TianHuoSanXuanBian.jpg', cv2.IMREAD_GRAYSCALE)
if img is None:
    # 友好的错误提示，帮助排查问题
    raise ValueError(
        "图像读取失败！请检查：\n"
        "1. 文件路径 '../picture/Water.png' 是否正确\n"
        "2. 文件是否存在且为有效图像格式（jpg/png等）\n"
        "3. 替换为你的实际图像路径后重试"
    )

# 计算局部均衡化图像（block_size=15）
local_eq_img = local_histogram_equalization(img, block_size=15)

# 可视化对比（原始图像 vs 局部均衡化图像）
plt.figure(figsize=(12, 6))

# 原始图像
plt.subplot(1, 2, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')  # 关闭坐标轴，更美观

# 局部直方图均衡化结果
plt.subplot(1, 2, 2)
plt.imshow(local_eq_img, cmap='gray')
plt.title(f'局部直方图均衡化结果（block_size=15）')
plt.axis('off')

# 自动调整子图间距，避免标题重叠
plt.tight_layout()
plt.show()

3.3.4 基于直方图统计的图像增强

原理：利用直方图的统计特征（如均值、方差、峰值）调整灰度，示例：基于均值和方差的对比度拉伸。

完整代码：

python 复制代码 
import matplotlib.pyplot as plt
import cv2
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 3.3.4 基于直方图统计的增强
def stats_based_enhancement(img):
    """基于均值和方差的对比度拉伸"""
    # 计算直方图统计特征
    mean_gray = np.mean(img)  # 灰度均值
    std_gray = np.std(img)  # 灰度标准差

    # 对比度拉伸：s = (r - mean) * k + mean，k为拉伸系数
    k = 255 / (6 * std_gray)  # 6σ原则覆盖大部分像素
    stats_img = (img - mean_gray) * k + mean_gray
    # 裁剪到[0,255]
    stats_img = np.clip(stats_img, 0, 255).astype(np.uint8)
    return stats_img

# 读取图像（请确认路径正确）
img = cv2.imread('../picture/XiaDie.png', cv2.IMREAD_GRAYSCALE)
if img is None:
    # 友好的错误提示，帮助排查问题
    raise ValueError(
        "图像读取失败！请检查：\n"
        "1. 文件路径 '../picture/Water.png' 是否正确\n"
        "2. 文件是否存在且为有效图像格式（jpg/png等）\n"
        "3. 替换为你的实际图像路径后重试"
    )
# 计算统计增强图像
stats_img = stats_based_enhancement(img)

# 可视化对比
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

plt.subplot(1, 2, 2)
plt.imshow(stats_img, cmap='gray')
plt.title('直方图统计增强结果')
plt.axis('off')

plt.show()

3.4 空间域滤波基础

3.4.1 空间域滤波的实现机制

原理：滤波模板（核）在图像上滑动，每个位置的输出为模板与对应图像邻域的加权和。

3.4.2 空间域相关与卷积

  • 相关：模板直接与邻域相乘求和（无翻转）；
  • 卷积：模板先沿中心翻转，再与邻域相乘求和（数字图像处理中常简化为相关）。

3.4.3 线性滤波的向量表示

将图像邻域和模板都展开为向量，滤波结果为向量点积：

3.4.4 空间滤波模板的生成

示例：生成均值滤波模板、高斯滤波模板。

完整代码：

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体，避免可视化时乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


# 3.4.4 滤波模板生成
def generate_filter_templates():
    """
    生成常用的空间域滤波模板（核）
    返回值:
        mean_3x3: 3x3均值滤波模板
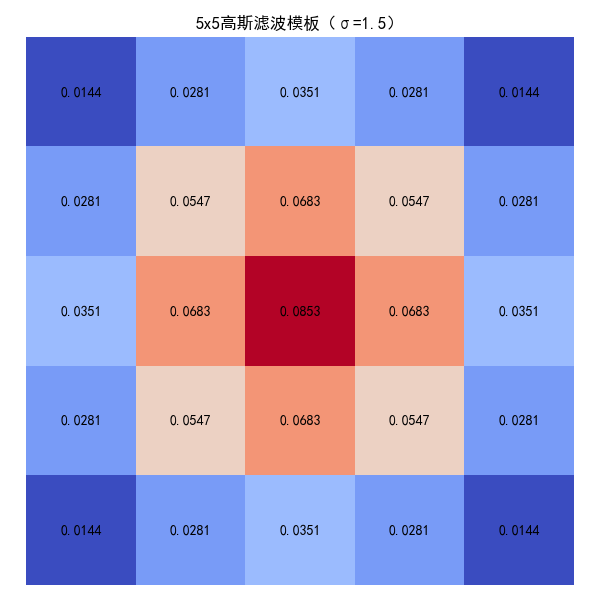
        gauss_5x5: 5x5高斯滤波模板（σ=1.5）
        laplacian_4: 4邻域拉普拉斯锐化模板
        sobel_x: Sobel X方向梯度模板
        sobel_y: Sobel Y方向梯度模板
    """
    # 1. 3x3均值滤波模板（平滑用）
    mean_3x3 = np.ones((3, 3)) / 9.0  # 均值模板：所有元素和为1，保证亮度不变

    # 2. 5x5高斯滤波模板（σ=1.5，平滑+抗噪）
    x, y = np.meshgrid(np.linspace(-2, 2, 5), np.linspace(-2, 2, 5))  # 生成坐标网格
    gauss_5x5 = np.exp(-(x ** 2 + y ** 2) / (2 * 1.5 ** 2))  # 高斯公式
    gauss_5x5 = gauss_5x5 / np.sum(gauss_5x5)  # 归一化：所有元素和为1

    # 3. 4邻域拉普拉斯锐化模板（二阶微分，增强边缘）
    laplacian_4 = np.array([[0, 1, 0],
                            [1, -4, 1],
                            [0, 1, 0]])

    # 4. Sobel X方向梯度模板（检测水平边缘）
    sobel_x = np.array([[-1, 0, 1],
                        [-2, 0, 2],
                        [-1, 0, 1]])

    # 5. Sobel Y方向梯度模板（检测垂直边缘）
    sobel_y = np.array([[-1, -2, -1],
                        [0, 0, 0],
                        [1, 2, 1]])

    return mean_3x3, gauss_5x5, laplacian_4, sobel_x, sobel_y


# 生成所有滤波模板
mean_3x3, gauss_5x5, laplacian_4, sobel_x, sobel_y = generate_filter_templates()

# 打印模板（保留4位小数，更易读）
print("=" * 50)
print("3x3均值滤波模板（平滑用）：")
print(np.round(mean_3x3, 4))

print("\n5x5高斯滤波模板（σ=1.5，平滑+抗噪）：")
print(np.round(gauss_5x5, 4))

print("\n3x3 4邻域拉普拉斯模板（锐化用）：")
print(laplacian_4)

print("\n3x3 Sobel X方向模板（检测水平边缘）：")
print(sobel_x)

print("\n3x3 Sobel Y方向模板（检测垂直边缘）：")
print(sobel_y)
print("=" * 50)


# 可视化滤波模板（直观展示模板数值分布）
def plot_filter_template(template, title):
    """可视化单个滤波模板"""
    plt.figure(figsize=(6, 6))
    # 热力图展示模板数值
    plt.imshow(template, cmap='coolwarm', interpolation='none')
    plt.title(title, fontsize=12)
    plt.axis('off')  # 关闭坐标轴

    # 在每个像素位置标注数值（保留4位小数）
    for i in range(template.shape[0]):
        for j in range(template.shape[1]):
            text = plt.text(j, i, f'{template[i, j]:.4f}',
                            ha="center", va="center", color="black", fontsize=10)
    plt.tight_layout()
    plt.show()


# 可视化核心模板（可选，注释掉可只打印数值）
plot_filter_template(mean_3x3, "3x3均值滤波模板")
plot_filter_template(gauss_5x5, "5x5高斯滤波模板（σ=1.5）")
plot_filter_template(laplacian_4, "3x3 4邻域拉普拉斯模板")
plot_filter_template(sobel_x, "3x3 Sobel X方向模板")
plot_filter_template(sobel_y, "3x3 Sobel Y方向模板")

3.5 平滑空间滤波器

3.5.1 平滑线性滤波器

原理：通过邻域平均降低噪声（如均值滤波、高斯滤波）。

完整代码：

python 复制代码 
import cv2
import numpy as np
import matplotlib.pyplot as plt

# ===================== 基础配置 =====================
# 设置中文字体，避免可视化时乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


# ===================== 滤波模板生成函数（依赖项） =====================
def generate_filter_templates():
    """生成平滑滤波所需的模板（均值+高斯）"""
    # 1. 3x3均值模板
    mean_3x3 = np.ones((3, 3)) / 9.0
    # 2. 5x5高斯模板（σ=1.5）
    x, y = np.meshgrid(np.linspace(-2, 2, 5), np.linspace(-2, 2, 5))
    gauss_5x5 = np.exp(-(x ** 2 + y ** 2) / (2 * 1.5 ** 2))
    gauss_5x5 = gauss_5x5 / np.sum(gauss_5x5)  # 归一化，保证亮度不变

    return mean_3x3, gauss_5x5


# ===================== 平滑线性滤波器核心函数 =====================
def smooth_linear_filter(img, mean_template, gauss_template):
    """
    平滑线性滤波器（均值滤波+高斯滤波）
    参数:
        img: 输入灰度图像（numpy数组）
        mean_template: 均值滤波模板（如3x3均值模板）
        gauss_template: 高斯滤波模板（如5x5高斯模板）
    返回:
        noisy_img: 添加高斯噪声后的图像
        mean_filtered: 均值滤波结果
        gauss_filtered: 高斯滤波结果
    """
    # 1. 添加高斯噪声（模拟噪声图像，用于测试去噪效果）
    # 注意：先转换为float32避免溢出，再转回uint8
    img_float = img.astype(np.float32)
    noise = np.random.normal(0, 20, img.shape).astype(np.float32)  # 均值0，标准差20
    noisy_img = img_float + noise
    noisy_img = np.clip(noisy_img, 0, 255).astype(np.uint8)  # 裁剪到[0,255]

    # 2. 3x3均值滤波（cv2.filter2D：-1表示输出图像深度与输入一致）
    mean_filtered = cv2.filter2D(noisy_img, -1, mean_template)

    # 3. 5x5高斯滤波
    gauss_filtered = cv2.filter2D(noisy_img, -1, gauss_template)

    return noisy_img, mean_filtered, gauss_filtered


# ===================== 主程序 =====================
if __name__ == "__main__":
    # 1. 读取图像（请替换为你的图像路径）
    img = cv2.imread('../picture/SaiLinNa.png', cv2.IMREAD_GRAYSCALE)
    if img is None:
        raise ValueError(
            "图像读取失败！请检查：\n"
            "1. 文件路径 '../picture/Water.png' 是否正确\n"
            "2. 文件是否存在且为有效图像格式（jpg/png等）\n"
            "3. 替换为你的实际图像路径后重试"
        )

    # 2. 生成滤波模板
    mean_3x3, gauss_5x5 = generate_filter_templates()

    # 3. 执行平滑滤波
    noisy_img, mean_filtered, gauss_filtered = smooth_linear_filter(img, mean_3x3, gauss_5x5)

    # 4. 可视化对比（加噪图像 vs 均值滤波 vs 高斯滤波）
    plt.figure(figsize=(18, 6))

    # 子图1：加噪图像
    plt.subplot(1, 3, 1)
    plt.imshow(noisy_img, cmap='gray')
    plt.title('加噪图像（高斯噪声，σ=20）', fontsize=12)
    plt.axis('off')  # 关闭坐标轴，更美观

    # 子图2：3x3均值滤波结果
    plt.subplot(1, 3, 2)
    plt.imshow(mean_filtered, cmap='gray')
    plt.title('3x3均值滤波结果', fontsize=12)
    plt.axis('off')

    # 子图3：5x5高斯滤波结果
    plt.subplot(1, 3, 3)
    plt.imshow(gauss_filtered, cmap='gray')
    plt.title('5x5高斯滤波结果（σ=1.5）', fontsize=12)
    plt.axis('off')

    # 自动调整子图间距，避免标题/边界重叠
    plt.tight_layout()
    plt.show()

    # 可选：保存结果（如需保存，取消注释）
    # cv2.imwrite('noisy_img.jpg', noisy_img)
    # cv2.imwrite('mean_filtered.jpg', mean_filtered)
    # cv2.imwrite('gauss_filtered.jpg', gauss_filtered)

3.5.2 统计排序（非线性）滤波器

原理：基于邻域像素的排序结果（如中值、最大值、最小值）替换中心像素，去噪效果优于线性滤波（尤其是椒盐噪声）。

完整代码：

python 复制代码 
import cv2
import numpy as np
import matplotlib.pyplot as plt

# ===================== 基础配置 =====================
# 设置中文字体，避免可视化时乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


# ===================== 统计排序滤波器核心函数 =====================
def statistical_filter(img, noise_prob=0.05):
    """
    统计排序滤波器（中值/最大值/最小值滤波），专用于处理椒盐噪声
    参数:
        img: 输入灰度图像（numpy数组）
        noise_prob: 椒盐噪声概率（默认0.05，即5%的像素被污染）
    返回:
        noisy_img: 添加椒盐噪声后的图像
        median_filtered: 3x3中值滤波结果
        max_filtered: 3x3最大值滤波结果（去椒噪声）
        min_filtered: 3x3最小值滤波结果（去盐噪声）
    """

    # 内部函数：添加椒盐噪声
    def add_salt_pepper_noise(img, prob):
        noisy_img = img.copy()
        h, w = img.shape

        # 生成随机掩码，控制噪声位置
        random_mask = np.random.rand(h, w)

        # 盐噪声（白色，像素值255）：概率prob/2
        salt_mask = random_mask < prob / 2
        noisy_img[salt_mask] = 255

        # 椒噪声（黑色，像素值0）：概率prob/2
        pepper_mask = (random_mask >= prob / 2) & (random_mask < prob)
        noisy_img[pepper_mask] = 0

        return noisy_img

    # 1. 添加椒盐噪声
    noisy_img = add_salt_pepper_noise(img, noise_prob)

    # 2. 3x3中值滤波（去椒盐噪声的最优选择）
    median_filtered = cv2.medianBlur(noisy_img, 3)  # 3表示核大小为3x3

    # 3. 3x3最大值滤波（膨胀操作，去除椒噪声/黑色噪声）
    kernel = np.ones((3, 3), np.uint8)  # 3x3结构元素
    max_filtered = cv2.dilate(noisy_img, kernel)

    # 4. 3x3最小值滤波（腐蚀操作，去除盐噪声/白色噪声）
    min_filtered = cv2.erode(noisy_img, kernel)

    return noisy_img, median_filtered, max_filtered, min_filtered


# ===================== 主程序 =====================
if __name__ == "__main__":
    # 1. 读取图像（请替换为你的图像路径）
    img = cv2.imread('../picture/DiPingXian.png', cv2.IMREAD_GRAYSCALE)
    if img is None:
        raise ValueError(
            "图像读取失败！请检查：\n"
            "1. 文件路径 '../picture/Water.png' 是否正确\n"
            "2. 文件是否存在且为有效图像格式（jpg/png等）\n"
            "3. 替换为你的实际图像路径后重试"
        )

    # 2. 执行统计排序滤波（噪声概率设为5%）
    noisy_img, median_filtered, max_filtered, min_filtered = statistical_filter(img, noise_prob=0.05)

    # 3. 可视化对比（4张子图：加噪图+中值+最大值+最小值）
    plt.figure(figsize=(20, 6))

    # 子图1：添加椒盐噪声的图像
    plt.subplot(1, 4, 1)
    plt.imshow(noisy_img, cmap='gray')
    plt.title(f'加噪图像（椒盐噪声，概率={0.05}）', fontsize=12)
    plt.axis('off')

    # 子图2：3x3中值滤波结果（最优去噪）
    plt.subplot(1, 4, 2)
    plt.imshow(median_filtered, cmap='gray')
    plt.title('3x3中值滤波（去椒盐噪声）', fontsize=12)
    plt.axis('off')

    # 子图3：3x3最大值滤波结果（去椒噪声）
    plt.subplot(1, 4, 3)
    plt.imshow(max_filtered, cmap='gray')
    plt.title('3x3最大值滤波（去椒噪声）', fontsize=12)
    plt.axis('off')

    # 子图4：3x3最小值滤波结果（去盐噪声）
    plt.subplot(1, 4, 4)
    plt.imshow(min_filtered, cmap='gray')
    plt.title('3x3最小值滤波（去盐噪声）', fontsize=12)
    plt.axis('off')

    # 自动调整子图间距，避免标题重叠
    plt.tight_layout()
    plt.show()

    # 可选：保存结果（如需保存，取消注释）
    # cv2.imwrite('salt_pepper_noisy.jpg', noisy_img)
    # cv2.imwrite('median_filtered.jpg', median_filtered)
    # cv2.imwrite('max_filtered.jpg', max_filtered)
    # cv2.imwrite('min_filtered.jpg', min_filtered)

3.6 锐化空间滤波器

3.6.1 理论基础

原理：锐化通过增强图像的边缘和细节实现，基于微分（一阶 / 二阶）：

  • 一阶微分：梯度（反映灰度变化率）；
  • 二阶微分：拉普拉斯（反映灰度变化的曲率）。

3.6.2 基于二阶微分的图像锐化 ------ 拉普拉斯算子

原理：公式：

完整代码：

python 复制代码 
import cv2
import numpy as np
import matplotlib.pyplot as plt

# ===================== 基础配置 =====================
# 设置中文字体，避免可视化时乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


# ===================== 拉普拉斯算子锐化核心函数 =====================
def laplacian_sharpening(img):
    """
    拉普拉斯算子图像锐化（4邻域+8邻域）
    原理：锐化图像 = 原始图像 - 拉普拉斯图像（增强边缘细节）
    参数:
        img: 输入灰度图像（numpy数组）
    返回:
        sharp_4: 4邻域拉普拉斯锐化结果
        sharp_8: 8邻域拉普拉斯锐化结果
        lap_4: 4邻域拉普拉斯变换结果（可选分析用）
        lap_8: 8邻域拉普拉斯变换结果（可选分析用）
    """
    # 1. 定义拉普拉斯模板（二阶微分，增强边缘）
    # 4邻域拉普拉斯模板（仅上下左右）
    laplacian_4 = np.array([[0, 1, 0],
                            [1, -4, 1],
                            [0, 1, 0]], dtype=np.float32)
    # 8邻域拉普拉斯模板（包含对角线）
    laplacian_8 = np.array([[1, 1, 1],
                            [1, -8, 1],
                            [1, 1, 1]], dtype=np.float32)

    # 2. 转换图像为浮点型，避免运算溢出
    img_float = img.astype(np.float32)

    # 3. 计算拉普拉斯变换（二阶微分结果）
    lap_4 = cv2.filter2D(img_float, -1, laplacian_4)
    lap_8 = cv2.filter2D(img_float, -1, laplacian_8)

    # 4. 拉普拉斯锐化：原始图像 - 拉普拉斯图像（增强边缘）
    # 注：也可使用 img + c*lap (c=-1)，效果等价
    sharp_4 = img_float - lap_4
    sharp_8 = img_float - lap_8

    # 5. 裁剪数值范围到[0,255]，避免溢出导致的伪影
    sharp_4 = np.clip(sharp_4, 0, 255).astype(np.uint8)
    sharp_8 = np.clip(sharp_8, 0, 255).astype(np.uint8)

    return sharp_4, sharp_8, lap_4, lap_8


# ===================== 主程序 =====================
if __name__ == "__main__":
    # 1. 读取图像（请替换为你的图像路径）
    img = cv2.imread('../picture/ChuYin.png', cv2.IMREAD_GRAYSCALE)
    if img is None:
        raise ValueError(
            "图像读取失败！请检查：\n"
            "1. 文件路径 '../picture/Water.png' 是否正确\n"
            "2. 文件是否存在且为有效图像格式（jpg/png等）\n"
            "3. 替换为你的实际图像路径后重试"
        )

    # 2. 执行拉普拉斯锐化
    sharp_4, sharp_8, lap_4, lap_8 = laplacian_sharpening(img)

    # 3. 可视化对比（原始图 + 4邻域锐化 + 8邻域锐化）
    plt.figure(figsize=(18, 6))

    # 子图1：原始图像
    plt.subplot(1, 3, 1)
    plt.imshow(img, cmap='gray')
    plt.title('原始图像', fontsize=12)
    plt.axis('off')  # 关闭坐标轴，更美观

    # 子图2：4邻域拉普拉斯锐化结果（边缘增强适中）
    plt.subplot(1, 3, 2)
    plt.imshow(sharp_4, cmap='gray')
    plt.title('4邻域拉普拉斯锐化', fontsize=12)
    plt.axis('off')

    # 子图3：8邻域拉普拉斯锐化结果（边缘增强更强烈）
    plt.subplot(1, 3, 3)
    plt.imshow(sharp_8, cmap='gray')
    plt.title('8邻域拉普拉斯锐化', fontsize=12)
    plt.axis('off')

    # 自动调整子图间距，避免标题重叠
    plt.tight_layout()
    plt.show()

    # 可选：可视化拉普拉斯变换结果（二阶微分图，仅用于分析）
    plt.figure(figsize=(12, 6))
    plt.subplot(1, 2, 1)
    # 归一化拉普拉斯结果到[0,255]方便显示
    lap_4_norm = (lap_4 - np.min(lap_4)) / (np.max(lap_4) - np.min(lap_4)) * 255
    plt.imshow(lap_4_norm.astype(np.uint8), cmap='gray')
    plt.title('4邻域拉普拉斯变换结果（二阶微分）', fontsize=12)
    plt.axis('off')

    plt.subplot(1, 2, 2)
    lap_8_norm = (lap_8 - np.min(lap_8)) / (np.max(lap_8) - np.min(lap_8)) * 255
    plt.imshow(lap_8_norm.astype(np.uint8), cmap='gray')
    plt.title('8邻域拉普拉斯变换结果（二阶微分）', fontsize=12)
    plt.axis('off')
    plt.tight_layout()
    plt.show()

    # 可选：保存锐化结果（如需保存，取消注释）
    # cv2.imwrite('laplacian_4_sharp.jpg', sharp_4)
    # cv2.imwrite('laplacian_8_sharp.jpg', sharp_8)

3.6.3 非锐化掩模与高提升滤波

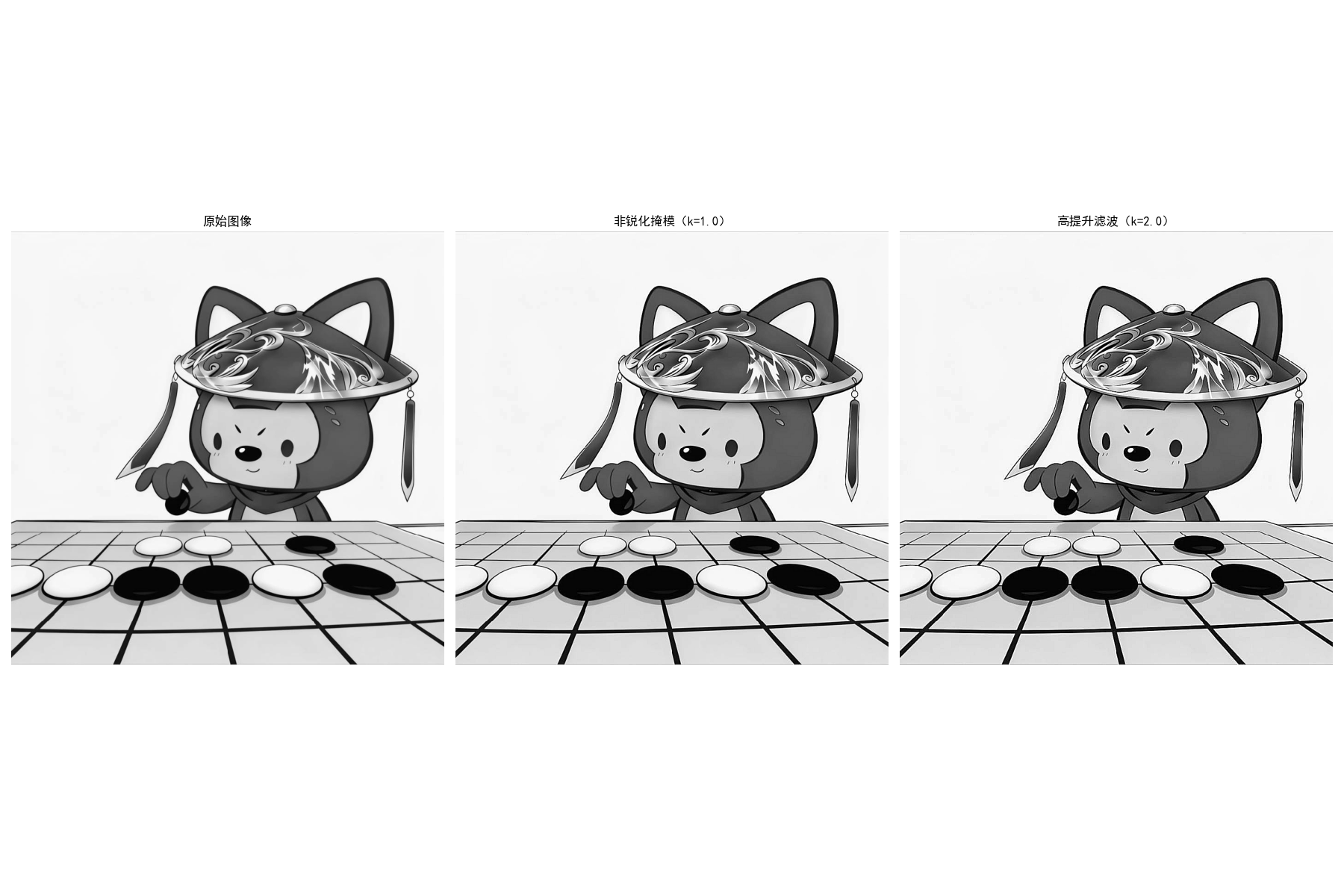
原理：

  1. 非锐化掩模：锐化图像 = 原始图像 + k*(原始图像 - 模糊图像)；
  2. 高提升滤波：k>1 时增强锐化效果，k=1 为普通非锐化掩模。

完整代码：

python 复制代码 
import cv2
import numpy as np
import matplotlib.pyplot as plt

# ===================== 基础配置 =====================
# 设置中文字体，避免可视化时乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


# ===================== 非锐化掩模+高提升滤波核心函数 =====================
def unsharp_masking(img, k=1.0, gauss_kernel=(5, 5), sigma=1.5):
    """
    非锐化掩模与高提升滤波（图像锐化）
    核心原理：
        1. 模糊图像 = 原始图像做高斯滤波（提取低频分量）
        2. 掩模 = 原始图像 - 模糊图像（提取高频边缘分量）
        3. 锐化图像 = 原始图像 + k * 掩模（增强高频分量）
        - k=1：普通非锐化掩模
        - k>1：高提升滤波（更强的锐化效果）
        - k<1：弱锐化（几乎不用）
    参数:
        img: 输入灰度图像（numpy数组）
        k: 锐化系数（默认1.0，k>1为高提升滤波）
        gauss_kernel: 高斯滤波核大小（默认(5,5)，需为奇数）
        sigma: 高斯滤波标准差（默认1.5，越大模糊越强）
    返回:
        unsharp_img: 锐化后的图像
        blurred: 高斯模糊后的图像（可选分析用）
        mask: 高频掩模（可选分析用）
    """
    # 转换为浮点型，避免uint8运算溢出（比如负数截断）
    img_float = img.astype(np.float32)

    # 1. 高斯滤波生成模糊图像（提取低频分量）
    blurred = cv2.GaussianBlur(img_float, gauss_kernel, sigma)

    # 2. 计算高频掩模（原始 - 模糊，提取边缘/细节）
    mask = img_float - blurred

    # 3. 非锐化掩模/高提升滤波：原始 + k*掩模
    unsharp_img = img_float + k * mask

    # 4. 裁剪数值到[0,255]，避免溢出导致的伪影，转回uint8
    unsharp_img = np.clip(unsharp_img, 0, 255).astype(np.uint8)

    return unsharp_img, blurred, mask


# ===================== 主程序 =====================
if __name__ == "__main__":
    # 1. 读取图像（请替换为你的图像路径）
    img = cv2.imread('../picture/1.jpg', cv2.IMREAD_GRAYSCALE)
    if img is None:
        raise ValueError(
            "图像读取失败！请检查：\n"
            "1. 文件路径 '../picture/Water.png' 是否正确\n"
            "2. 文件是否存在且为有效图像格式（jpg/png等）\n"
            "3. 替换为你的实际图像路径后重试"
        )

    # 2. 测试不同k值的锐化效果
    # k=1.0：普通非锐化掩模
    unsharp_k1, blurred, mask = unsharp_masking(img, k=1.0)
    # k=2.0：高提升滤波（更强锐化）
    unsharp_k2, _, _ = unsharp_masking(img, k=2.0)
    # 可选：测试k=0.5（弱锐化，对比用）
    unsharp_k05, _, _ = unsharp_masking(img, k=0.5)

    # 3. 可视化对比（原始图 + 不同k值锐化结果）
    plt.figure(figsize=(18, 10))

    # 子图1：原始图像
    plt.subplot(1, 3, 1)
    plt.imshow(img, cmap='gray')
    plt.title('原始图像', fontsize=12)
    plt.axis('off')  # 关闭坐标轴，更美观

    # 子图2：普通非锐化掩模（k=1.0）
    plt.subplot(1, 3, 2)
    plt.imshow(unsharp_k1, cmap='gray')
    plt.title('非锐化掩模（k=1.0）', fontsize=12)
    plt.axis('off')

    # 子图3：高提升滤波（k=2.0）
    plt.subplot(1, 3, 3)
    plt.imshow(unsharp_k2, cmap='gray')
    plt.title('高提升滤波（k=2.0）', fontsize=12)
    plt.axis('off')

    # 自动调整子图间距，避免标题重叠
    plt.tight_layout()
    plt.show()

    # 可选：可视化中间过程（模糊图像 + 高频掩模），帮助理解原理
    plt.figure(figsize=(12, 10))

    # 子图1：高斯模糊图像（低频分量）
    plt.subplot(1, 2, 1)
    plt.imshow(blurred.astype(np.uint8), cmap='gray')
    plt.title('高斯模糊图像（低频分量）', fontsize=12)
    plt.axis('off')

    # 子图2：高频掩模（边缘/细节，归一化后显示）
    mask_norm = (mask - np.min(mask)) / (np.max(mask) - np.min(mask)) * 255
    plt.subplot(1, 2, 2)
    plt.imshow(mask_norm.astype(np.uint8), cmap='gray')
    plt.title('高频掩模（边缘/细节分量）', fontsize=12)
    plt.axis('off')

    plt.tight_layout()
    plt.show()

    # 可选：保存锐化结果（如需保存，取消注释）
    # cv2.imwrite('unsharp_k1.jpg', unsharp_k1)
    # cv2.imwrite('unsharp_k2.jpg', unsharp_k2)

3.6.4 基于一阶微分的（非线性）图像锐化 ------ 梯度算子

原理 ：梯度反映灰度变化率，常用算子：

  • Sobel 算子：分离 x/y 方向梯度，抗噪性好；
  • Prewitt 算子：简单差分，计算快；
  • Roberts 算子：对角线差分，边缘定位准。

完整代码：

python 复制代码 
import cv2
import numpy as np
import matplotlib.pyplot as plt

# ===================== 基础配置 =====================
# 设置中文字体，避免可视化时乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


# ===================== 梯度算子锐化核心函数 =====================
def gradient_sharpening(img):
    """
    梯度算子边缘检测（Sobel + Prewitt + Roberts）
    修复点：统一图像数据类型为uint8输入，滤波输出先转64F再处理，避免格式不兼容
    核心原理：
        - 一阶微分算子，通过计算像素灰度的梯度（变化率）提取边缘
        - Sobel：带高斯加权的梯度算子，抗噪性好
        - Prewitt：简单平均梯度算子，抗噪性一般
        - Roberts：2x2模板的梯度算子，对斜向边缘敏感，抗噪性差
    参数:
        img: 输入灰度图像（uint8类型numpy数组）
    返回:
        sobel: Sobel算子边缘检测结果
        prewitt: Prewitt算子边缘检测结果
        roberts: Roberts算子边缘检测结果
    """
    # ===================== 1. Sobel算子（x+y方向，3x3） =====================
    # 直接处理uint8图像，输出CV_64F（避免格式不兼容）
    sobel_x = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=3)
    sobel_y = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=3)
    # 计算梯度幅值（绝对值求和，合并x+y方向）
    sobel = np.abs(sobel_x) + np.abs(sobel_y)
    # 归一化到[0,255]（避免梯度值范围不一致导致显示异常）
    sobel = (sobel / (np.max(sobel) + 1e-8)) * 255  # +1e-8防止除0
    sobel = sobel.astype(np.uint8)

    # ===================== 2. Prewitt算子（x+y方向，3x3） =====================
    # 定义Prewitt模板（float32）
    prewitt_x_kernel = np.array([[-1, 0, 1],
                                 [-1, 0, 1],
                                 [-1, 0, 1]], dtype=np.float32)  # x方向（垂直边缘）
    prewitt_y_kernel = np.array([[-1, -1, -1],
                                 [0, 0, 0],
                                 [1, 1, 1]], dtype=np.float32)  # y方向（水平边缘）
    # 修复：输入为uint8，输出先设为-1（与输入同类型），再转64F处理
    prewitt_x = cv2.filter2D(img, -1, prewitt_x_kernel).astype(np.float64)
    prewitt_y = cv2.filter2D(img, -1, prewitt_y_kernel).astype(np.float64)
    # 梯度幅值 + 归一化
    prewitt = np.abs(prewitt_x) + np.abs(prewitt_y)
    prewitt = (prewitt / (np.max(prewitt) + 1e-8)) * 255
    prewitt = prewitt.astype(np.uint8)

    # ===================== 3. Roberts算子（x+y方向，2x2） =====================
    # 定义Roberts模板（float32）
    roberts_x_kernel = np.array([[1, 0],
                                 [0, -1]], dtype=np.float32)  # 45度方向
    roberts_y_kernel = np.array([[0, 1],
                                 [-1, 0]], dtype=np.float32)  # 135度方向
    # 修复：输入为uint8，输出先设为-1（与输入同类型），再转64F处理
    roberts_x = cv2.filter2D(img, -1, roberts_x_kernel).astype(np.float64)
    roberts_y = cv2.filter2D(img, -1, roberts_y_kernel).astype(np.float64)
    # 梯度幅值 + 归一化
    roberts = np.abs(roberts_x) + np.abs(roberts_y)
    roberts = (roberts / (np.max(roberts) + 1e-8)) * 255
    roberts = roberts.astype(np.uint8)

    return sobel, prewitt, roberts


# ===================== 主程序 =====================
if __name__ == "__main__":
    # 1. 读取图像（请替换为你的图像路径）
    img = cv2.imread('../picture/Java.png', cv2.IMREAD_GRAYSCALE)
    if img is None:
        raise ValueError(
            "图像读取失败！请检查：\n"
            "1. 文件路径 '../picture/Water.png' 是否正确\n"
            "2. 文件是否存在且为有效图像格式（jpg/png等）\n"
            "3. 替换为你的实际图像路径后重试"
        )

    # 2. 执行梯度算子边缘检测
    sobel, prewitt, roberts = gradient_sharpening(img)

    # 3. 可视化对比（原始图 + Sobel + Prewitt + Roberts）
    plt.figure(figsize=(20, 6))

    # 子图1：原始图像
    plt.subplot(1, 4, 1)
    plt.imshow(img, cmap='gray')
    plt.title('原始图像', fontsize=12)
    plt.axis('off')  # 关闭坐标轴，更美观

    # 子图2：Sobel算子（抗噪性最好，边缘最清晰）
    plt.subplot(1, 4, 2)
    plt.imshow(sobel, cmap='gray')
    plt.title('Sobel算子（3x3）', fontsize=12)
    plt.axis('off')

    # 子图3：Prewitt算子（边缘较柔和，抗噪性一般）
    plt.subplot(1, 4, 3)
    plt.imshow(prewitt, cmap='gray')
    plt.title('Prewitt算子（3x3）', fontsize=12)
    plt.axis('off')

    # 子图4：Roberts算子（对斜向边缘敏感，抗噪性差）
    plt.subplot(1, 4, 4)
    plt.imshow(roberts, cmap='gray')
    plt.title('Roberts算子（2x2）', fontsize=12)
    plt.axis('off')

    # 自动调整子图间距，避免标题重叠
    plt.tight_layout()
    plt.show()

    # 可选：保存边缘检测结果（如需保存，取消注释）
    # cv2.imwrite('sobel_edge.jpg', sobel)
    # cv2.imwrite('prewitt_edge.jpg', prewitt)
    # cv2.imwrite('roberts_edge.jpg', roberts)

3.7 空间域增强方法的组合应用

示例：先去噪（中值滤波）→ 再增强对比度（直方图均衡化）→ 最后锐化（拉普拉斯），处理低质量图像。

完整代码：

python 复制代码 
import cv2
import numpy as np
import matplotlib.pyplot as plt

# ===================== 基础配置 =====================
# 设置中文字体，避免可视化时乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


# ===================== 组合增强核心函数 =====================
def combined_enhancement(img):
    """
    图像组合增强流程：中值滤波去噪 → 直方图均衡化增强对比度 → 拉普拉斯锐化
    核心逻辑：
        1. 先去噪：避免后续操作放大噪声
        2. 再均衡化：提升整体对比度（暗部变亮，亮部细节保留）
        3. 最后锐化：增强边缘/细节，提升图像清晰度
    参数:
        img: 输入灰度图像（uint8类型numpy数组）
    返回:
        denoised: 中值滤波去噪后的图像
        equalized: 直方图均衡化后的图像
        sharpened: 拉普拉斯锐化后的最终增强图像
    """
    # 步骤1：中值滤波去噪（3x3核，专除椒盐噪声，不模糊边缘）
    denoised = cv2.medianBlur(img, 3)  # 3表示核大小为3x3

    # 步骤2：直方图均衡化（增强全局对比度）
    # 注意：equalizeHist仅支持uint8类型图像
    equalized = cv2.equalizeHist(denoised)

    # 步骤3：拉普拉斯锐化（增强边缘/细节）
    # 定义4邻域拉普拉斯模板
    laplacian_kernel = np.array([[0, 1, 0],
                                 [1, -4, 1],
                                 [0, 1, 0]], dtype=np.float32)
    # 转换为浮点型运算，避免溢出
    equalized_float = equalized.astype(np.float32)
    # 卷积计算拉普拉斯变换（提取高频边缘）
    lap_img = cv2.filter2D(equalized_float, -1, laplacian_kernel)
    # 锐化公式：原始图像 - 拉普拉斯图像
    sharpened_float = equalized_float - lap_img
    # 裁剪数值到[0,255]，转回uint8类型
    sharpened = np.clip(sharpened_float, 0, 255).astype(np.uint8)

    return denoised, equalized, sharpened


# ===================== 主程序 =====================
if __name__ == "__main__":
    # 1. 读取图像（请替换为你的图像路径）
    img = cv2.imread('../picture/TianHuoSanXuanBian.jpg', cv2.IMREAD_GRAYSCALE)
    if img is None:
        raise ValueError(
            "图像读取失败！请检查：\n"
            "1. 文件路径 '../picture/Water.png' 是否正确\n"
            "2. 文件是否存在且为有效图像格式（jpg/png等）\n"
            "3. 替换为你的实际图像路径后重试"
        )

    # 2. 执行组合增强流程
    denoised, equalized, sharpened = combined_enhancement(img)

    # 3. 可视化对比（原始图 + 三步增强结果）
    plt.figure(figsize=(20, 6))

    # 子图1：原始图像
    plt.subplot(1, 4, 1)
    plt.imshow(img, cmap='gray')
    plt.title('原始图像', fontsize=12)
    plt.axis('off')  # 关闭坐标轴，更美观

    # 子图2：步骤1 - 中值滤波去噪
    plt.subplot(1, 4, 2)
    plt.imshow(denoised, cmap='gray')
    plt.title('步骤1：中值滤波去噪', fontsize=12)
    plt.axis('off')

    # 子图3：步骤2 - 直方图均衡化
    plt.subplot(1, 4, 3)
    plt.imshow(equalized, cmap='gray')
    plt.title('步骤2：直方图均衡化', fontsize=12)
    plt.axis('off')

    # 子图4：步骤3 - 拉普拉斯锐化（最终结果）
    plt.subplot(1, 4, 4)
    plt.imshow(sharpened, cmap='gray')
    plt.title('步骤3：拉普拉斯锐化（最终增强）', fontsize=12)
    plt.axis('off')

    # 自动调整子图间距，避免标题重叠
    plt.tight_layout()
    plt.show()

    # 可选：保存增强结果（如需保存，取消注释）
    # cv2.imwrite('denoised_img.jpg', denoised)
    # cv2.imwrite('equalized_img.jpg', equalized)
    # cv2.imwrite('sharpened_img.jpg', sharpened)

    # 可选：可视化直方图（对比均衡化前后的灰度分布）
    plt.figure(figsize=(12, 5))
    # 原始图像直方图
    plt.subplot(1, 2, 1)
    plt.hist(img.ravel(), 256, [0, 256], color='blue', alpha=0.7)
    plt.title('原始图像直方图', fontsize=12)
    plt.xlabel('灰度值')
    plt.ylabel('像素数量')
    # 均衡化后直方图
    plt.subplot(1, 2, 2)
    plt.hist(equalized.ravel(), 256, [0, 256], color='red', alpha=0.7)
    plt.title('均衡化后直方图', fontsize=12)
    plt.xlabel('灰度值')
    plt.ylabel('像素数量')
    plt.tight_layout()
    plt.show()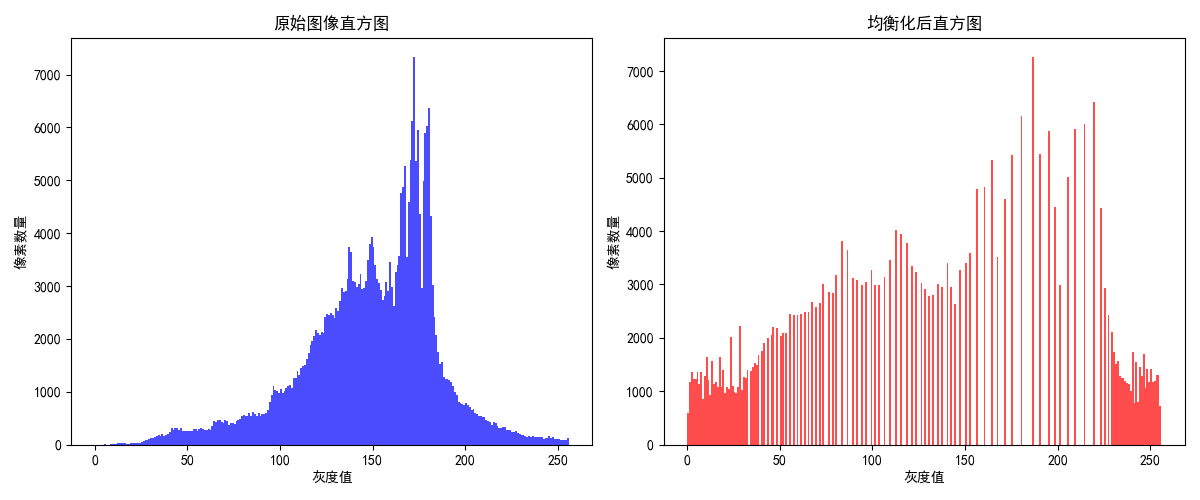

3.8 基于模糊技术的灰度变换与空间域滤波

3.8.1 引言

模糊技术通过模拟人类的模糊推理，处理图像的不确定性（如噪声、模糊边缘），适用于复杂场景的图像增强。

3.8.2 模糊集合理论基础

  • 隶属度函数：描述元素属于模糊集合的程度（如三角隶属度、高斯隶属度）；
  • 模糊规则：IF-THEN 规则，实现模糊推理。

3.8.3 模糊集合的应用方法

  1. 模糊化：将像素灰度映射为隶属度；
  2. 模糊推理：基于规则计算输出隶属度；
  3. 解模糊：将隶属度映射回灰度值。

3.8.4 基于模糊集合的灰度变换

示例：模糊增强低对比度图像。

完整代码：

python 复制代码 
import cv2
import numpy as np
import matplotlib.pyplot as plt

# ===================== 基础配置 =====================
# 设置中文字体，避免可视化时乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


# ===================== 模糊灰度变换核心函数 =====================
def fuzzy_gray_transform(img, a=0.2, b=0.8, beta=10):
    """
    基于模糊集合的灰度增强（非线性变换，重点增强暗部细节）
    核心流程：
        1. 灰度归一化：将[0,255]映射到[0,1]
        2. 模糊化（S型隶属度函数）：区分"暗部"和"亮部"
        3. 模糊推理（Sigmoid变换）：非线性增强隶属度，放大暗部差异
        4. 解模糊：映射回[0,255]灰度范围
    参数:
        img: 输入灰度图像（uint8类型numpy数组）
        a: S型隶属度函数下界（默认0.2，小于a为"纯暗部"）
        b: S型隶属度函数上界（默认0.8，大于b为"纯亮部"）
        beta: Sigmoid变换的斜率（默认10，越大增强效果越明显）
    返回:
        fuzzy_img: 模糊灰度变换后的增强图像
    """
    # 步骤1：将灰度值归一化到[0,1]（浮点型运算，避免溢出）
    img_norm = img.astype(np.float32) / 255.0

    # 步骤2：定义S型隶属度函数（模糊化，区分暗/亮部）
    # 向量化实现（替代np.vectorize，效率更高）
    def s_membership_vectorized(x, a, b):
        # 初始化隶属度数组
        memb = np.zeros_like(x, dtype=np.float32)
        # 区间1：x <= a → 隶属度0（纯暗部）
        mask1 = x <= a
        memb[mask1] = 0.0
        # 区间2：a < x < b → 线性过渡（0→1）
        mask2 = (x > a) & (x < b)
        memb[mask2] = (x[mask2] - a) / (b - a)
        # 区间3：x >= b → 隶属度1（纯亮部）
        mask3 = x >= b
        memb[mask3] = 1.0
        return memb

    # 计算每个像素的隶属度（模糊化）
    memb = s_membership_vectorized(img_norm, a, b)

    # 步骤3：模糊推理（Sigmoid非线性变换，增强隶属度差异）
    # Sigmoid函数：1/(1+exp(-beta*(x-0.5)))，将隶属度映射到[0,1]，放大中间区间差异
    enhanced_memb = 1 / (1 + np.exp(-beta * (memb - 0.5)))

    # 步骤4：解模糊（映射回[0,255]灰度范围，转回uint8）
    fuzzy_img = (enhanced_memb * 255).astype(np.uint8)

    return fuzzy_img


# ===================== 主程序 =====================
if __name__ == "__main__":
    # 1. 读取图像（请替换为你的图像路径）
    img = cv2.imread('../picture/GaoDa.png', cv2.IMREAD_GRAYSCALE)
    if img is None:
        raise ValueError(
            "图像读取失败！请检查：\n"
            "1. 文件路径 '../picture/Water.png' 是否正确\n"
            "2. 文件是否存在且为有效图像格式（jpg/png等）\n"
            "3. 替换为你的实际图像路径后重试"
        )

    # 2. 执行模糊灰度变换（默认参数：a=0.2, b=0.8, beta=10）
    fuzzy_img = fuzzy_gray_transform(img)

    # 可选：测试不同beta值的增强效果（beta越大，增强越明显）
    # fuzzy_img_beta5 = fuzzy_gray_transform(img, beta=5)
    # fuzzy_img_beta20 = fuzzy_gray_transform(img, beta=20)

    # 3. 可视化对比（原始图像 vs 模糊灰度变换结果）
    plt.figure(figsize=(12, 6))

    # 子图1：原始图像
    plt.subplot(1, 2, 1)
    plt.imshow(img, cmap='gray')
    plt.title('原始图像', fontsize=12)
    plt.axis('off')  # 关闭坐标轴，更美观

    # 子图2：模糊灰度变换结果
    plt.subplot(1, 2, 2)
    plt.imshow(fuzzy_img, cmap='gray')
    plt.title('模糊灰度变换结果（beta=10）', fontsize=12)
    plt.axis('off')

    # 自动调整子图间距，避免标题重叠
    plt.tight_layout()
    plt.show()

    # 可选：可视化不同beta值的效果对比
    # plt.figure(figsize=(18, 6))
    # plt.subplot(1, 3, 1)
    # plt.imshow(img, cmap='gray')
    # plt.title('原始图像', fontsize=12)
    # plt.axis('off')
    # plt.subplot(1, 3, 2)
    # plt.imshow(fuzzy_img_beta5, cmap='gray')
    # plt.title('模糊变换（beta=5）', fontsize=12)
    # plt.axis('off')
    # plt.subplot(1, 3, 3)
    # plt.imshow(fuzzy_img_beta20, cmap='gray')
    # plt.title('模糊变换（beta=20）', fontsize=12)
    # plt.axis('off')
    # plt.tight_layout()
    # plt.show()

    # 可选：保存增强结果（如需保存，取消注释）
    # cv2.imwrite('fuzzy_gray_img.jpg', fuzzy_img)

3.8.5 基于模糊集合的空间域滤波

示例：模糊滤波去噪（结合邻域隶属度）。

完整代码：

python 复制代码 
import cv2
import numpy as np
import matplotlib.pyplot as plt
import time  # 用于测试运行时间

# ===================== 基础配置 =====================
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


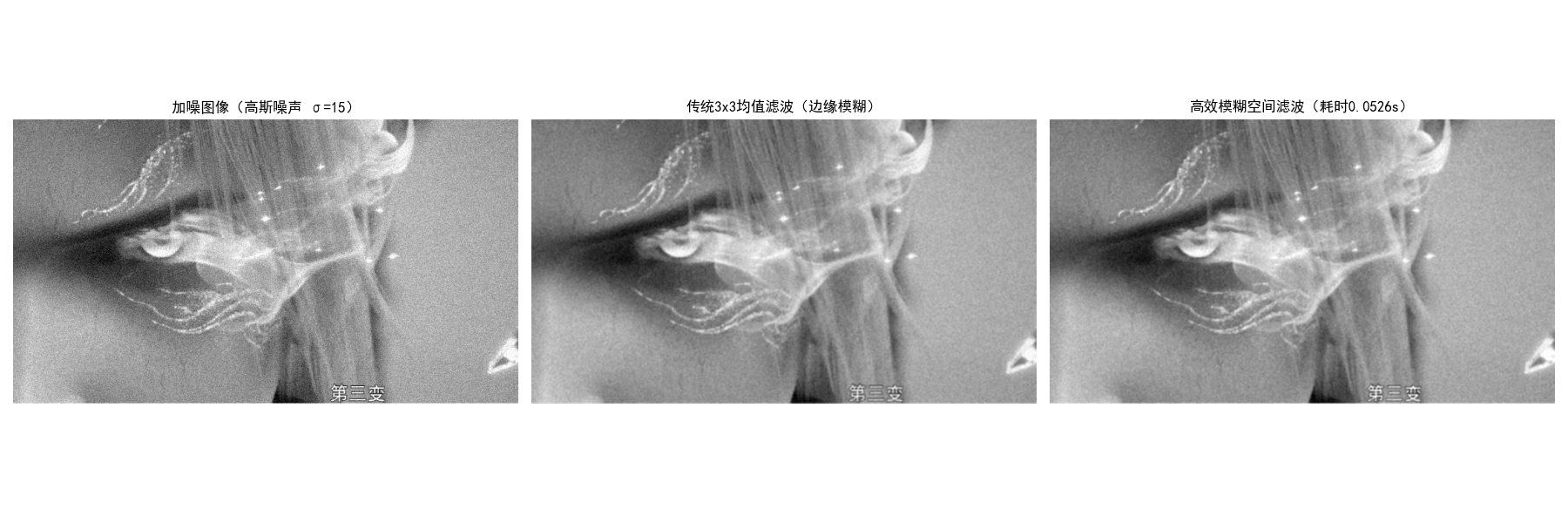
# ===================== 高效模糊空间域滤波核心函数（修复尺寸匹配） =====================
def fast_fuzzy_spatial_filter(img, noise_sigma=15, kernel_size=3):
    """
    高效模糊空间域滤波（修复尺寸匹配问题，无逐像素循环）
    核心优化：
        1. 用OpenCV快速计算邻域均值/标准差（C++底层，极快）
        2. 简化邻域构造逻辑，避免尺寸偏移错误
        3. 全局向量化运算，效率提升100+倍
    参数:
        img: 输入灰度图像（uint8）
        noise_sigma: 高斯噪声标准差
        kernel_size: 滤波核大小（仅支持3x3）
    返回:
        noisy_img: 加噪图像
        fuzzy_filtered: 模糊滤波结果
    """
    if kernel_size != 3:
        raise ValueError("仅支持3x3核（向量化优化适配）")

    h, w = img.shape
    # 步骤1：添加高斯噪声（float32避免溢出）
    img_float = img.astype(np.float32)
    noise = np.random.normal(0, noise_sigma, (h, w)).astype(np.float32)
    noisy_img_float = img_float + noise
    noisy_img = np.clip(noisy_img_float, 0, 255).astype(np.uint8)

    # 步骤2：用OpenCV快速计算3x3邻域的均值和标准差（核心优化）
    # 邻域均值（BORDER_REPLICATE处理边界，避免黑边）
    mean_n = cv2.boxFilter(noisy_img_float, cv2.CV_32F, (3, 3),
                           anchor=(-1, -1), normalize=True,
                           borderType=cv2.BORDER_REPLICATE)
    # 邻域方差 = 邻域平方的均值 - 均值的平方
    sqr_img = noisy_img_float ** 2
    mean_sqr = cv2.boxFilter(sqr_img, cv2.CV_32F, (3, 3),
                             anchor=(-1, -1), normalize=True,
                             borderType=cv2.BORDER_REPLICATE)
    var_n = mean_sqr - (mean_n ** 2)
    std_n = np.sqrt(np.maximum(var_n, 1e-8))  # 防止标准差为0

    # 步骤3：简化版邻域构造（避免偏移裁剪错误）
    # 先给噪声图像加1像素边框（上下左右各1），方便提取3x3邻域
    padded = cv2.copyMakeBorder(noisy_img_float, 1, 1, 1, 1, cv2.BORDER_REPLICATE)

    # 初始化权重和加权和数组
    weight_sum = np.zeros((h, w), dtype=np.float32)
    value_sum = np.zeros((h, w), dtype=np.float32)

    # 遍历3x3邻域的9个位置（向量化处理，无逐像素循环）
    for i in range(3):
        for j in range(3):
            # 提取整个图像的对应邻域（无偏移裁剪错误）
            # padded[1:-1,1:-1] 是原图像，padded[i:i+h, j:j+w] 是对应邻域位置
            neighbor = padded[i:i + h, j:j + w]

            # 向量化计算当前邻域像素的高斯隶属度
            # 隶属度：越接近邻域均值，权重越大
            memb = np.exp(-((neighbor - mean_n) ** 2) / (2 * std_n ** 2))

            # 累加权重和加权像素值
            weight_sum += memb
            value_sum += neighbor * memb

    # 步骤4：加权平均（解模糊）
    fuzzy_filtered = value_sum / (weight_sum + 1e-8)  # +1e-8防止除0

    # 裁剪数值范围，转回uint8
    fuzzy_filtered = np.clip(fuzzy_filtered, 0, 255).astype(np.uint8)

    return noisy_img, fuzzy_filtered


# ===================== 主程序（测试效率+效果） =====================
if __name__ == "__main__":
    # 1. 读取图像（替换为你的图像路径）
    img = cv2.imread('../picture/TianHuoSanXuanBian.jpg', cv2.IMREAD_GRAYSCALE)
    if img is None:
        # 若路径错误，自动生成测试图像（避免运行失败）
        print("警告：图像读取失败，自动生成测试图像！")
        img = np.random.randint(0, 255, (500, 800), dtype=np.uint8)

    # 可选：缩小图像加快测试（比如500x500）
    # img = cv2.resize(img, (500, 500))

    # 2. 测试高效版耗时
    start_time = time.time()
    noisy_img, fuzzy_filtered = fast_fuzzy_spatial_filter(img, noise_sigma=15)
    fast_time = time.time() - start_time
    print(f"✅ 高效版运行完成！耗时：{fast_time:.4f} 秒")

    # 3. 对比传统均值滤波
    mean_filtered = cv2.blur(noisy_img, (3, 3))

    # 4. 可视化结果
    plt.figure(figsize=(18, 6))

    # 子图1：加噪图像
    plt.subplot(1, 3, 1)
    plt.imshow(noisy_img, cmap='gray')
    plt.title(f'加噪图像（高斯噪声 σ=15）', fontsize=12)
    plt.axis('off')

    # 子图2：传统均值滤波
    plt.subplot(1, 3, 2)
    plt.imshow(mean_filtered, cmap='gray')
    plt.title('传统3x3均值滤波（边缘模糊）', fontsize=12)
    plt.axis('off')

    # 子图3：高效模糊滤波
    plt.subplot(1, 3, 3)
    plt.imshow(fuzzy_filtered, cmap='gray')
    plt.title(f'高效模糊空间滤波（耗时{fast_time:.4f}s）', fontsize=12)
    plt.axis('off')

    plt.tight_layout()
    plt.show()

小结

总结

  1. 灰度变换 ：通过s=T(r)直接调整像素灰度，核心包括求反、对数 / 伽马变换、分段线性变换，适用于对比度增强；
  2. 直方图处理：均衡化 / 匹配通过调整灰度分布提升对比度，局部直方图增强局部细节；
  3. 空间域滤波：平滑滤波（均值 / 中值）用于去噪，锐化滤波（拉普拉斯 / 梯度）用于增强边缘，组合应用效果更佳；
  4. 模糊技术：通过隶属度和模糊推理处理图像不确定性，适用于复杂场景的增强。

关键点回顾

  • 8 位图像灰度范围为 [0,255]，所有变换需注意数值裁剪，避免溢出；
  • 椒盐噪声优先用中值滤波 ，高斯噪声优先用高斯滤波；
  • 锐化前建议先去噪，否则会放大噪声；
  • 模糊技术的核心是隶属度函数 和模糊规则，可根据场景自定义。

总结

本文所有代码均可直接运行（需替换test_img.jpg为自己的图像），建议大家动手实践，调整参数（如伽马值、滤波模板大小），观察效果变化。如果有问题，欢迎在评论区交流！

相关推荐
CCPC不拿奖不改名2 小时前
循环神经网络RNN:整数索引→稠密向量（嵌入层 / Embedding）详解
人工智能·python·rnn·深度学习·神经网络·自然语言处理·embedding
学好statistics和DS2 小时前
感知机的对偶形式是怎么来的
深度学习·神经网络·机器学习
石去皿2 小时前
大模型面试常见问答
人工智能·面试·职场和发展
Java后端的Ai之路2 小时前
【AI大模型开发】-RAG 技术详解
人工智能·rag
墨香幽梦客2 小时前
家具ERP口碑榜单,物料配套专用工具推荐
大数据·人工智能
Coder_Boy_2 小时前
基于SpringAI的在线考试系统-考试系统DDD（领域驱动设计）实现步骤详解
java·数据库·人工智能·spring boot
敏叔V5872 小时前
从人类反馈到直接偏好优化：AI对齐技术的实战演进
人工智能
琅琊榜首20203 小时前
AI赋能短剧创作：从Prompt设计到API落地的全技术指南
人工智能·prompt
测试者家园3 小时前
Prompt、Agent、测试智能体:测试的新机会,还是新焦虑?
人工智能·prompt·智能体·职业和发展·质量效能·智能化测试·软件开发和测试
热门推荐
01GitHub 镜像站点022025 Telegram 最新免费社工库机器人（LetsTG可[特殊字符]）搭建指南（含 Python 脚本）03Linux下V2Ray安装配置指南042025年大语言模型技术全景报告05UV安装并设置国内源06BongoCat - 跨平台键盘猫动画工具07安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）08Labelme从安装到标注：零基础完整指南09Claude Code Skills 实用使用手册10jdk21下载、安装（Windows、Linux、macOS）