目录
[Batch Normalization批量标准化](#Batch Normalization批量标准化)
摘要
本周继续学习尚硅谷深度学习教程,学习内容是参数初始化的相关方法和正则化相关内容
1.参数初始化
参数初始化方案的选择在神经网络学习中起着举足轻重的作用,它对保持数值稳定性至关重要。此外,这些初始化方案的选择可以与激活函数的选择有趣的结合在一起。我们选择哪个激活函数以及如何初始化参数,可以决定优化算法收敛的速度有多快;糟糕选择可能会导致我们在训练时遇到梯度爆炸或梯度消失。
常数初始化
所有权重参数初始化为一个常数,即
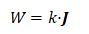
这里J 为全1矩阵,k为初始化的常数。
注意:将权重初始值设为0将无法正确进行学习。严格地说,不能将权重初始值设成一样的值。因为这意味着反向传播时权重全部都会进行相同的更新,被更新为相同的值(对称的值)。这使得神经网络拥有许多不同的权重的意义丧失了。为了防止"权重均一化"(瓦解权重的对称结构),必须随机生成初始值。
秩初始化
权重参数初始化为单位矩阵,即
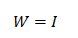
这里I为单位矩阵,即主对角线上元素为1,其它元素为0。
正态分布初始化
权重参数按指定均值μ 与标准差σ 正态分布初始化。因为不能直接将权重初始化为相同的常数,所以需要对参数进行随机初始化。最常见的随机分布就是 正态分布 (也叫 高斯分布),记作 X ~ N (μ , σ2)。
其概率密度函数为:
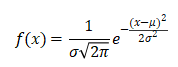
均匀分布初始化
权重参数在指定区间内均匀分布初始化。均匀分布一般记作 X ~ U (a , b)。
其概率密度函数为:
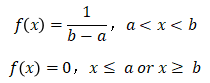
Xavier初始化(Glorot初始化)
Xavier初始化根据输入和输出的神经元数量调整权重的初始范围,确保每一层的输出方差与输入方差相近。
Xavier正态分布初始化:均值为0,标准差为的正态分布
Xavier均匀分布初始化:区间[,
]内均匀分布
其中表示输入数,
表示输出数
Xavier初始化参数适用于Sigmoid和Tanh等激活函数,能有效缓解梯度消失或爆炸问题。
He初始化(Kaiming初始化)
He初始化根据输入的神经元数量调整权重的初始范围。
He正态分布初始化:均值为0,标准差为的正态分布。
He均匀分布初始化:区间[,
]内均匀分布。
其中表示输入数。
He初始化参数主要适用于ReLU及其变体(如Leaky ReLU)激活函数。
2.正则化
机器学习的问题中,过拟合 是一个很常见的问题。
过拟合指的是能较好拟合训练数据,但不能很好地拟合不包含在训练数据中的其他数据。机器学习的目标是提高泛化能力,希望即便是不包含在训练数据里的未观测数据,模型也可以进行正确的预测。因此可以通过 正则化 方法来抑制过拟合。
常用的正则化方法有Batch Normalization、权值衰减、Dropout、早停法等。
Batch Normalization批量标准化
Batch Normalization最重要的目的,其实是调整各层的激活值分布使其拥有适当的广度,BN层通常放在线性层(全连接层/卷积层)之后,激活函数之前。它有着以下优点:
- 可以使学习快速进行(允许更高的学习率)
- 不那么依赖初始值(对于初始值不用那么神经质)
- 抑制过拟合(降低Dropout等的必要性)
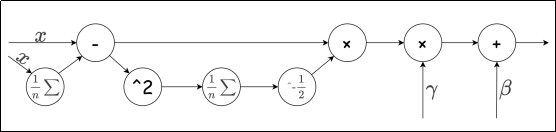
Batch Normalization会先对数据进行标准化,再对数据进行缩放和平移:

下图为Batch Normalization的计算图:
权值衰减
通过在学习的过程中对大的权重进行"惩罚",可以有效地抑制过拟合,这种方法被称为 权值衰减。因为很多过拟合产生的原因,就是权重参数取值过大。
一般会对损失函数加上一个权重的范数;最常见的就是 L2 范数的平方:

惩罚项求导之后得到
;所以在求权重梯度时,需要为之前误差反向传播法的结果,再加上
。
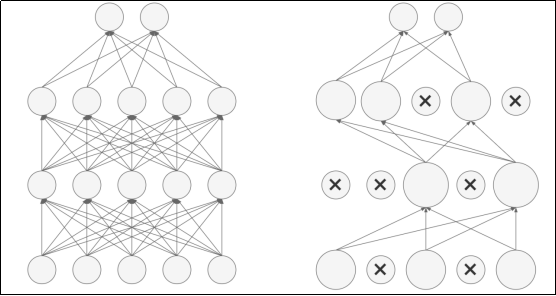
Dropout随机失活
Dropout(随机失活,暂退法)是一种在学习的过程中随机关闭神经元的方法。
训练时以概率随机关闭神经元,迫使网络不依赖特定神经元,增强鲁棒性,同时未被关闭的神经元的输出值以
的比例进行缩放,以保持期望值不变;而测试时通常不使用Dropout,即所有神经元保持激活状态并且不进行缩放。
Dropout会有隐式集成的效果(每次迭代训练不同的子网络,测试时近似集成效果)。
Dropout在全连接层和卷积层均适用,尤其对大规模网络效果显著。Dropout通常放在激活函数之后,线性层(全连接层/卷积层)之前。