
层序遍历
cpp
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
// 创建一个队列用于层序遍历(BFS)
queue<TreeNode*> que;
// 如果根节点不为空,将其加入队列
if (root != NULL) que.push(root);
// 用于存储结果的变量,初始化为0
int result = 0;
// 层序遍历主循环:当队列不为空时继续处理
while (!que.empty()) {
// 获取当前层的节点数量
// 注意:size在循环开始时获取,保证只处理当前层的节点
int size = que.size();
// 遍历当前层的所有节点
for (int i = 0; i < size; i++) {
// 从队列中取出当前节点
TreeNode* node = que.front();
que.pop();
// 关键:如果是当前层的第一个节点(最左边的节点)
// 更新result为该节点的值
// 由于层序遍历是从上到下、从左到右,所以最后记录的
// result就是最后一层最左边的节点的值
if (i == 0) result = node->val; // 记录最后一行第一个元素
// 如果当前节点有左子节点,将其加入队列
// 注意:左子节点先加入队列,保证下一层的顺序也是从左到右
if (node->left) que.push(node->left);
// 如果当前节点有右子节点,将其加入队列
if (node->right) que.push(node->right);
}
// 当前层处理完毕,继续处理下一层
// 注意:result会在每一层都被更新为当前层最左边的节点值
// 当最后一层处理完毕后,result就是最后一层最左边的节点值
}
// 返回结果:最后一层最左边的节点值
return result;
}
};-
关键点:
-
使用
i == 0判断是否是当前层的第一个节点(最左边的节点) -
每一层都会更新
result为该层第一个节点的值 -
由于层序遍历顺序,最后更新的
result就是最后一层最左边的节点值
-
二叉树递归法
cpp
class Solution {
public:
// 全局变量:记录遍历过程中找到的最大深度
int maxDepth = INT_MIN; // 初始化为整数最小值,确保第一个深度能更新它
// 全局变量:记录最深层最左边节点的值
int result;
// 递归遍历函数(深度优先搜索)
// 参数:
// root: 当前节点
// depth: 当前节点所在的深度(根节点深度为0)
void traversal(TreeNode* root, int depth) {
// 基本情况:如果当前节点是叶子节点(没有左右子节点)
if (root->left == NULL && root->right == NULL) {
// 检查当前叶子节点的深度是否大于已知的最大深度
if (depth > maxDepth) {
// 如果更深,更新最大深度
maxDepth = depth;
// 更新结果为当前叶子节点的值
// 注意:由于是前序遍历(先左后右),所以最先访问到的
// 最深层叶子节点就是最左边的节点
result = root->val;
}
// 叶子节点处理完毕,返回上一层递归
return;
}
// 递归遍历左子树(如果存在)
if (root->left) {
depth++; // 深度加1,进入下一层
traversal(root->left, depth); // 递归调用左子树
depth--; // 回溯:深度减1,回到当前层
// 注意:depth是值传递,所以这里需要显式回溯
}
// 递归遍历右子树(如果存在)
if (root->right) {
depth++; // 深度加1,进入下一层
traversal(root->right, depth); // 递归调用右子树
depth--; // 回溯:深度减1,回到当前层
}
// 当前节点处理完毕,返回上一层递归
// 这个return是可选的,因为函数结束会自动返回
return;
}
// 主函数:找到树的最底层最左边的节点值
int findBottomLeftValue(TreeNode* root) {
// 从根节点开始深度优先遍历,初始深度为0
traversal(root, 0);
// 返回全局变量result中存储的结果
return result;
}
};
cpp
void traversal(TreeNode* root, int depth) {
// 这个函数是void类型,不返回值
// 这里的return只是结束当前函数调用
if (root->left == NULL && root->right == NULL) {
if (depth > maxDepth) {
//.........
}
return; // 只是结束递归,不返回任何值
}
// ...
return; // 函数结束,无返回值
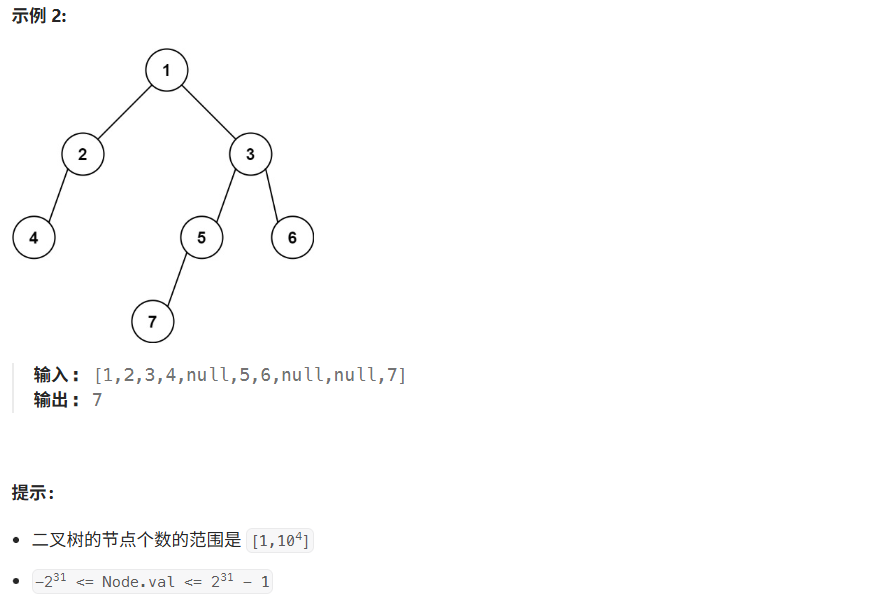
}举例: 1
/ \
2 3
/ / \
4 5 6
/
7 初始状态:
maxDepth = INT_MIN (-2147483648)
result = 未初始化步骤1:调用 findBottomLeftValue(1)
traversal(root=1, depth=0);步骤2:traversal(1, 0) 开始执行
cpp
// 节点1:不是叶子节点(有左右子节点)
// 进入左子树递归
depth++ // depth = 1
traversal(root=2, depth=1)步骤3:traversal(2, 1) 开始执行
cpp
// 节点2:不是叶子节点(有左子节点)
// 进入左子树递归
depth++ // depth = 2
traversal(root=4, depth=2)步骤4:traversal(4, 2) 开始执行
cpp
// 节点4:是叶子节点(left==NULL && right==NULL)
// depth=2, maxDepth=INT_MIN
// 条件:depth(2) > maxDepth(-2147483648) → true
maxDepth = depth = 2
result = root->val = 4
return;
// 返回到节点2步骤5:回到 traversal(2, 2)(注意:depth=2)
cpp
// 节点2继续执行
depth-- // depth = 1(回溯)
// 检查右子树:root->right == NULL,跳过
return; // 返回到节点1步骤6:回到 traversal(1, 1)(注意:depth=1)
cpp
// 节点1继续执行
depth-- // depth = 0(回溯)
// 进入右子树递归
depth++ // depth = 1
traversal(root=3, depth=1)步骤7:traversal(3, 1) 开始执行
.......
.......
.......
traversal(1, 0) 开始
├─ depth=1 → traversal(2, 1) 开始
│ ├─ depth=2 → traversal(4, 2) 开始
│ │ 找到叶子节点,maxDepth=2, result=4
│ │ traversal(4, 2) 结束
│ │
│ ├─ 回到traversal(2, 2)
│ │ depth=1(回溯)
│ │ traversal(2, 1) 结束
│ │
│ └─ traversal(2, 1) 结束
│
├─ 回到traversal(1, 1)
│ depth=0(回溯)
│
├─ depth=1 → traversal(3, 1) 开始
│ ├─ depth=2 → traversal(5, 2) 开始
│ │ ├─ depth=3 → traversal(7, 3) 开始
│ │ │ 找到叶子节点,maxDepth=3, result=7
│ │ │ traversal(7, 3) 结束
│ │ │
│ │ ├─ 回到traversal(5, 3)
│ │ │ depth=2(回溯)
│ │ │ traversal(5, 2) 结束
│ │ │
│ │ └─ traversal(5, 2) 结束
│ │
│ ├─ 回到traversal(3, 2)
│ │ depth=1(回溯)
│ │
│ ├─ depth=2 → traversal(6, 2) 开始
│ │ 叶子节点,但depth=2 < maxDepth=3,不更新
│ │ traversal(6, 2) 结束
│ │
│ ├─ 回到traversal(3, 2)
│ │ depth=1(回溯)
│ │ traversal(3, 1) 结束
│ │
│ └─ traversal(3, 1) 结束
│
└─ 回到traversal(1, 0)
结束