
🔥小龙报:个人主页
🎬作者简介:C++研发,嵌入式,机器人方向学习者
❄️个人专栏:《算法通关指南》
✨ 永远相信美好的事情即将发生

文章目录
- 前言
- 一、贪心
-
- [1.1 什么是贪心算法](#1.1 什么是贪心算法)
- [1.2 贪心算法的特点](#1.2 贪心算法的特点)
- [1.3 如何学习贪心?](#1.3 如何学习贪心?)
- 二、简单贪心的经典算法题
- 总结与每日励志
前言
本专栏聚焦算法题实战,系统讲解算法模块:以《c++编程》,《数据结构和算法》《基础算法》《算法实战》 等几个板块以题带点,讲解思路与代码实现,帮助大家快速提升代码能力ps:本章节题目分两部分,比较基础笔者只附上代码供大家参考,其他的笔者会附上自己的思考和讲解,希望和大家一起努力见证自己的算法成长
一、贪心
贪心算法是两极分化很严重的算法。简单的问题会让你觉得理所应当,难⼀点的问题会让你怀疑人生。在解决贪心问题我们有时不仅要理解贪心策略,也要学会证明贪心策略的正确性来提高思维的严密性。
1.1 什么是贪心算法
贪心算法也称作贪心策略:企图用局部最优找出全局最优。
(1)把解决问题的过程分成若干步;
(2)解决每⼀步时,都选择"当前看起来最优的"解法;
(3)希望"得到全局的最优解
1.2 贪心算法的特点
总体特点:目光短浅
(1)对于绝大多数题目,贪心策略的提出并不是很难,难的是证明它是正确的。因为贪心算法相较于暴力枚举,每一步并不是把所有情况都考虑进去,而是只考虑当前看起来最优的情况。但是局部最优并不等于全局最优,所以我们必须要能严谨的证明我们的贪心策略是正确的。⼀般证明策略有:反证法,数学归纳法,交换论证法等等。
(2)当问题的场景不同时,贪心的策略也会不同。因此,贪心策略的提出是没有固定的套路和模板的。
1.3 如何学习贪心?
(1)重点放在各种各样的策略上,把各种策略当成经验来吸收;
(2)在平常学习的时候,我们尽可能的证明⼀下这个贪心策略是否正确,这样有利于培养我们严谨的思维。# 二、简单贪心的经典算法题
二、简单贪心的经典算法题
2.1 最大子段和
2.1.1题目
链接:最大子段和

2.1.2 算法原理
贪心想法:从前往后累加,我们会遇到下面两种情况:
(1)目前的累加和 > 0 :那么当前累加和还会对后续的累加和做出贡献,那我们就继续向后累加,然后更新结果。
(2) 目前的累加和 < 0 :对后续的累加和做不了⼀点贡献,直接大胆舍弃计算过的这⼀段,把累加和重置为0,然后继续向后累加。
这样我们在扫描整个数组⼀遍之后,就能更新出最大子段和
注:考虑到如果结果可能为负数所以可以在累加过程中一边更新结果不用做过多断判断。全为负数时既为求最大值。
2.1.3代码
csharp
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
LL a[N];
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
LL sum = 0;
LL ret = -1e20;
for (int i = 1; i <= n; i++)
{
sum += a[i];
ret = max(ret, sum);
if (sum < 0)
sum = 0;
}
cout << ret << endl;
return 0;
}2.1.4 贪心策略证明
(1)证明方法:反证法
(2)证明思路:抓住向后加的时候,只要不小于0 ,就会⼀直加下的主线去在累加的过程中算出⼀段区间和sum[a,b] < 0,如果不舍弃这⼀段,那么 [a, b]段之间就会存在⼀点,「以某个位置为起点」就会「更优」,分为下面两种情况:
2.1.4.1证明过程:
(1)情况一:在ab段存在⼀个c点 ,从这个c位置开始,「不越过 」的累加和比从a开始的累加和更优:(元素全为负数不考虑,因为全为负数时该贪心策略本身就是正确的)
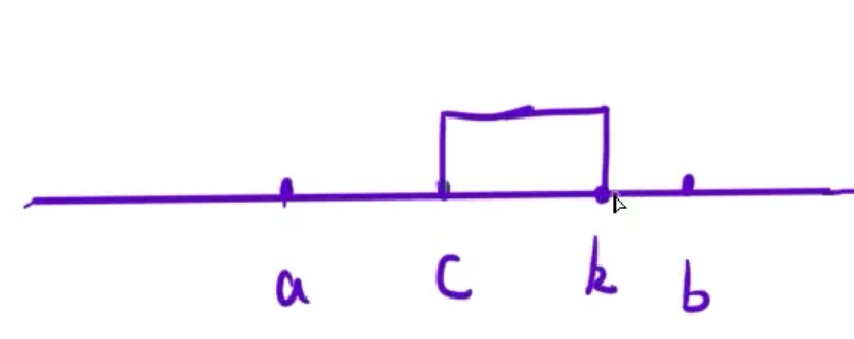
如果存在这⼀点,那么sum[c,k] > sum[a,k],但是如果sum[c,k] > sum[a,k],那么sum[a,c −1] < 0,这与我们的贪心策略矛盾既在区间加上元素b之前,区间中任意以a为左端点的一个子区间区间和都大于0。故该情况不成立的.
(2)情况二: 在ab段存在⼀个点c ,从这个位置开始,「越过b或者刚好在b」的累加和比从a开始的累加和更优:

如果存在这⼀点,那么:sum[c,b] > sum[a,b],但是如果sum[c,b] > sum[a,b],那么sum[a,c −1] < 0,与我们的贪心策略矛盾既在区间加上元素b之前,区间中任意以a为左端点的一个子区间区间和都大于0。故该情况不成立的.
故证毕
2.2 纪念品分组
2.2.1题目
链接:纪念品分组
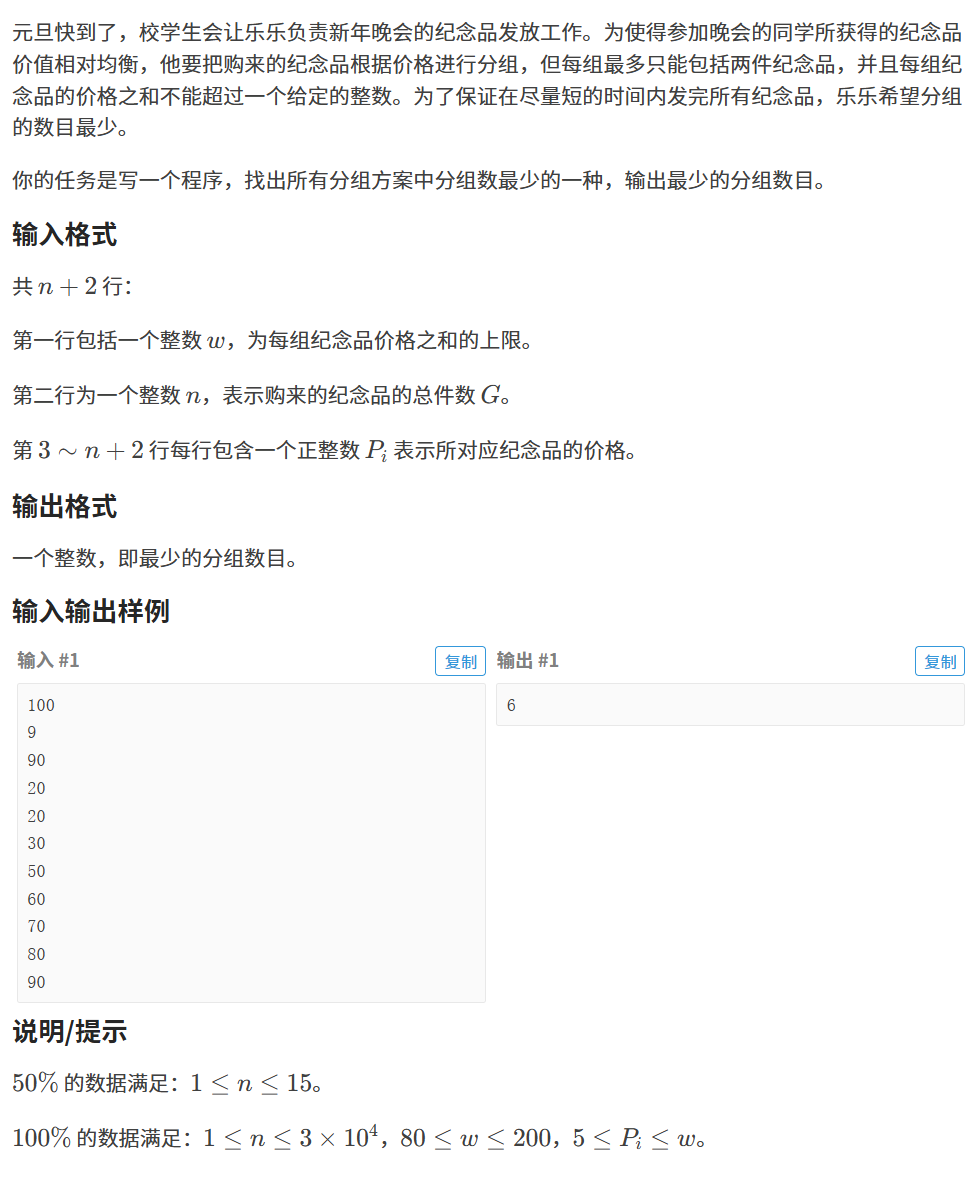
2.2.2 算法原理
先将所有的纪念品排序,每次拿出当前的最小 值x与最大值y:
(1)如果把x+y ≤w:就把这两个放在⼀起;
(2)如果x+y >w:说明此时最大的和谁都凑不到⼀起, y单独分组, x继续留下在进行下⼀次判断。
直到所有的物品都按照上述规则分配之后,得到的组数就是最优解
2.2.3代码
csharp
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 3e4 + 10;
int a[N];
int main()
{
int n,w;
cin >> w >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
sort(a + 1, a + 1 + n);
int l = 1, r = n;
int ret = 0;
while (l <= r) //相遇时给物品还未分配
{
if (a[l] + a[r] <= w)
{
l++;
r--;
}
else
r--;
ret++;
}
cout << ret << endl;
return 0;
}2.2.4 贪心策略证明
(1)证明方法:交换论证法
(2)证明思路:对于区间[ai...aj],如果存在最优解但是ai与aj的分配方式与我们贪心解的分配方式不一样,我们通过调整方式调整成贪心解
2.2.4.1证明过程:
(1) a[i] + a[j] > w时:
贪心解会把a[j]单独分组,a[i]留待下次考虑.
最优解也必定会把a[j]单独分组,因为没有更小的a[i]值与a[j]组合。此时贪心解与最优解一致。
(2)a[i] + a[j] ≤ w时:
贪心解会把两者组合分在一个组里面;最优解可能有以下几种情况
情况一:◦a[j]和a[k]和一组:
▪如果a[i]单独⼀组的话,a[j] + a[k]为一组,可以调整交换a[i]和a[k],此时并不影响结,与贪心解一致
▪如果a[i]和a[l]一组的话,交换a[l]和a[k],就会变成(a[i] + a[j]),(a[l] + a[k]),总体变成a[l] + a[k] ≤ a[j] + a[k] ≤ w,不影响最终结果,和贪心解⼀致
情况二:◦a[j]单独一组:
▪如果a[i]也单独⼀组的话,最优解还不如贪心解分的组少,矛盾。
▪如果a[i]和另⼀个a[k]组的话,我们可以把a[k]和a[j]交换,此时并不影响结,与贪心解一致
总之:综上所述,我们可以通过不断的「调整」,使的最优解在「不改变其最优性」的前提下,变得和贪心解一致。
总结与每日励志
✨本文介绍了贪心算法的基本概念、特点和学习方法,重点讲解了两道经典贪心算法题:最大子段和与纪念品分组。文章通过反证法和交换论证法严谨证明了贪心策略的正确性,并提供了相应的代码实现。贪心算法通过局部最优选择寻求全局最优解,虽然策略因问题而异,但掌握其证明方法能培养严密思维。作者鼓励读者保持积极心态,相信通过不断练习和思考能够提升算法能力。
