力扣每日一题 2026.1

本文整理了多类经典算法的核心思路与应用技巧，涵盖二分答案、并查集、BFS/DFS、动态规划、单调栈等高频考点。结合实际问题，拆解算法本质，分享反向思维、二维转一维等解题妙招，助力提升算法分析与问题求解能力。

目录

[1631. 最小体力消耗路径 （二分；类最小生成树）](#1631. 最小体力消耗路径 （二分；类最小生成树）)

[1970. 你能穿过矩阵的最后一天（上一题升级版）正删 反向加边](#1970. 你能穿过矩阵的最后一天（上一题升级版）正删 反向加边)

[1390. 因数个数为4的数 因数之和](#1390. 因数个数为4的数 因数之和)

[1161. 最大层内元素和 -- BFS 二叉树](#1161. 最大层内元素和 -- BFS 二叉树)

[1339. 分裂二叉树的最大乘积 -- 子树和 dfs](#1339. 分裂二叉树的最大乘积 -- 子树和 dfs)

[865. 具有所有最深节点的最小子树 -- dfs 求叶子节点的lca](#865. 具有所有最深节点的最小子树 -- dfs 求叶子节点的lca)

[712. 两个字符串的最小ASCII删除和 -- 编辑距离变形](#712. 两个字符串的最小ASCII删除和 -- 编辑距离变形)

[84. 柱状图中最大的矩形 -- 单调栈](#84. 柱状图中最大的矩形 -- 单调栈)

[85. 最大矩形 -- 84 题三维升级版](#85. 最大矩形 -- 84 题三维升级版)

---

1631. 最小体力消耗路径 （二分；类最小生成树）

最小化 从左上角走到右下角路径上相邻格子之间 高度差绝对值的最大值。

（看到 最小最大）解法1：二分答案（BFS验证答案 能不能扩展到右下角）

class Solution:
    def minimumEffortPath(self, h: List[List[int]]) -> int:
        m, n = len(h), len(h[0])
        left, right, ans = 0, 10**6 - 1, 0

        while left <= right:
            mid = left + right >> 1
            q = deque([(0, 0)])
            vis = set((0,0))
            
            # 扩展
            while q:
                x, y = q.popleft()
                for nx, ny in [(x - 1, y), (x + 1, y), (x, y - 1), (x, y + 1)]:
                    if 0 <= nx < m and 0 <= ny < n and (nx, ny) not in vis and abs(h[x][y] - h[nx][ny]) <= mid:
                        q.append((nx, ny))
                        vis.add((nx, ny))
            
            if (m - 1, n - 1) in vis:
                right = mid - 1
            else:
                left = mid + 1
        
        return left

还可以建模为图问题 ，节点中的边为上下、左右的，边权为节点差的绝对值。

类似最小生成树，实现左上和右下连通的最小边权要求。

可考虑 kruskal 式的并查集加边 ；或者 prim 式的扩展访问代价最小的边。

解法2：并查集模板

class UnionFind:
    def __init__(self, n: int):
        self.parent = list(range(n))
    
    def find(self, x: int) -> int:
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]
    
    def merge(self, x: int, y: int):
        x, y = self.find(x), self.find(y)
        self.parent[y] = x
    
    def connected(self, x: int, y: int) -> bool:
        return self.find(x) == self.find(y)

实现类似 kruskal

class Solution:
    def minimumEffortPath(self, h: List[List[int]]) -> int:
        m, n, edges = len(h), len(h[0]), []
        # 边权从小到大的边
        for i in range(m):
            for j in range(n):
                id = i * n + j
                if i > 0:
                    edges.append((id - n, id, abs(h[i][j] - h[i - 1][j])))
                if j > 0:
                    edges.append((id - 1, id, abs(h[i][j] - h[i][j - 1])))
        
        edges.sort(key=lambda e: e[2])
        uf = UnionFind(m * n)

        # 从小到大合并 直到联通
        for x, y, v in edges:
            uf.merge(x, y)
            if uf.connected(0, m * n - 1):
                return v

解法3：用 heapq 实现类似 prim

class Solution:
    def minimumEffortPath(self, h: List[List[int]]) -> int:
        m, n = len(h), len(h[0])
        q = [(0, 0, 0)]
        dist = [0] + [float("inf")] * (m * n - 1)
        vis = set()

        while q:
            d, x, y = heapq.heappop(q) # 最小堆
            id = x * n + y
            if id in vis:
                continue
            if (x, y) == (m - 1, n - 1): # 到了
                break
            
            vis.add(id)
            # 扩展
            for nx, ny in [(x - 1, y), (x + 1, y), (x, y - 1), (x, y + 1)]:
                if 0 <= nx < m and 0 <= ny < n and max(d, abs(h[x][y] - h[nx][ny])) <= dist[nx * n + ny]:
                    dist[nx * n + ny] = max(d, abs(h[x][y] - h[nx][ny]))
                    heapq.heappush(q, (dist[nx * n + ny], nx, ny))
        
        return dist[m * n - 1] # 到终点的最小代价

1970. 你能穿过矩阵的最后一天（上一题升级版）正删 反向加边

第 i 天，坐标为 (r_i, c_i) 的陆地变成水。 问通过陆地，从最上一行到最下一行的最后一天。

（从前到后是删边 从后到前与上下左右加边；新陆地和老陆地连接）

最上一行和最小一行下标标为 n*m和n*m+1的话；第一行统一连 n*m；最后一行统一连 n*m+1；

（并查集模板同上）

class Solution:
    def latestDayToCross(self, m: int, n: int, cells: List[List[int]]) -> int:
        DIRS = (0, -1), (0, 1), (-1, 0), (1, 0)  # 左右上下
        top, bottom = m * n, m * n + 1
        uf = UnionFind(m * n + 2)
        land = [[False] * n for _ in range(m)]

        for day in range(len(cells) - 1, -1, -1):
            r, c = cells[day]
            r -= 1  # 改成从 0 开始的下标
            c -= 1
            v = r * n + c
            land[r][c] = True  # 变成陆地

            if r == 0:
                uf.merge(v, top)  # 与最上边相连

            if r == m - 1:
                uf.merge(v, bottom)  # 与最下边相连

            for dx, dy in DIRS:
                x, y = r + dx, c + dy
                if 0 <= x < m and 0 <= y < n and land[x][y]:
                    uf.merge(v, x * n + y)  # 与四周的陆地相连

            if uf.connected(top, bottom):  # 最上边和最下边连通
                return day

1390. 因数个数为4的数 因数之和

先预处理 每个数的因数个数以及因数和 ；类似埃氏筛向倍数扩展。

MX = 100_001
div_num = [0] * MX # 因数个数
div_sum = [0] * MX # 因数之和
for i in range(1, MX):
    for j in range(i, MX, i):  # 枚举 i 的倍数 j
        div_num[j] += 1  # i 是 j 的因子，统计因数个数
        div_sum[j] += i  #  统计因数和

class Solution:
    def sumFourDivisors(self, nums: List[int]) -> int:
        ans = 0
        for x in nums:
            if div_num[x] == 4:
                ans += div_sum[x]
        return ans

1161. 最大层内元素和 -- BFS 二叉树

二叉树 元素和最大的 层号。 逐层向下扩展 BFS。

class Solution:
    def maxLevelSum(self, root: Optional[TreeNode]) -> int:
        ans, maxx, level = 0, -inf, 1
        q = [root]

        while q:
            now = q # 这一层
            q, s = [], 0 # q 统计下一层
            for node in now:
                s += node.val
                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)
            
            if s > maxx:
                maxx, ans = s, level
            level += 1
            
        return ans

1339. 分裂二叉树的最大乘积 -- 子树和 dfs

删除一条边之后，二叉树变成 一个子树和剩余部分。

一遍 dfs 统计所有的子树和，并存在 sub 列表中。

max { s*(tt-s) }

class Solution:
    def maxProduct(self, root: Optional[TreeNode]) -> int:
        def dfs(node: Optional[TreeNode]) -> int:
            if node is None:
                return 0
            s = node.val + dfs(node.left) + dfs(node.right)
            sub.append(s)
            return s
        sub = []
        tt = dfs(root)
        return max(s * (tt-s) for s in sub) % 1_000_000_007

865. 具有所有最深节点的最小子树 -- dfs 求叶子节点的lca

找所有叶子节点的 LCA 。往下dfs 沿途统计每个子树的深度 max{左深，右深} +1。

每个子树逻辑一样：左子树深就是左子树的 L，右子树深就是右子树的 L，否则就为根节点 root。

class Solution:
    def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:
        def f(root):
            if not root:
                return 0, None

            d1, lca1 = f(root.left) # 左子树
            d2, lca2 = f(root.right) # 右子树
            
            # 返回深度和lca
            if d1 > d2:
                return d1 + 1, lca1
            if d1 < d2:
                return d2 + 1, lca2
            return d1 + 1, root

        return f(root)[1]

712. 两个字符串的最小ASCII删除和 -- 编辑距离变形

为使得两个字符串相同 最少删掉 字母数的ascll之和。

字符串匹配；编辑距离只有删的情形。

删掉最少 -> 保留最多；对于两个串的最后一个元素，假设相同则都保留；否则 max{删掉其中一个}

class Solution:
    def minimumDeleteSum(self, s1: str, s2: str) -> int:
        n, m = len(s1), len(s2)
        total = sum(map(ord, s1)) + sum(map(ord, s2))

        f = [[0] * (m + 1) for _ in range(n + 1)]
        for i, x in enumerate(s1):
            for j, y in enumerate(s2):
                if x == y: # 最后一位相等则保留
                    f[i + 1][j + 1] = f[i][j] + ord(x)
                else: # 否则往前一位匹配 比谁大
                    f[i + 1][j + 1] = max(f[i][j + 1], f[i + 1][j])

        return total - f[n][m] * 2 # ascll 总和 减去重叠的

84. 柱状图中最大的矩形 -- 单调栈

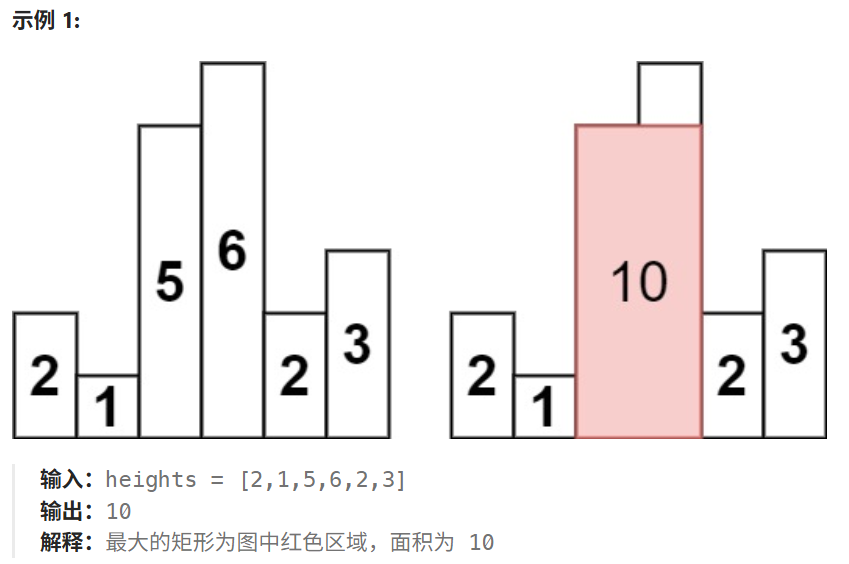
确定高度则，能到的最左边，就是左边最近的 小于的位置+1；（递增单调栈 实现）

最右边，就是右边最近的 小于的位置-1。（倒过来 递增单调栈）

可以三次遍历 分别统计 left[i] right[i] ；统计答案 max{ h[i]*(right[i]-left[i]) }

优化版：只需要一次遍历，把现在位置作为 right ，栈的第一 第二 元素分别作为 height 和 left。

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        heights.append(-1)
        st = [-1]  # 在栈中只有一个数的时候，栈顶的「下面那个数」是 -1，对应 left[i] = -1 的情况
        ans = 0
        for right, h in enumerate(heights): # 现在是right
            while len(st) > 1 and heights[st[-1]] >= h:
                i = st.pop()  # 矩形的高（的下标）
                left = st[-1]  # 栈顶下面那个数就是 left
                ans = max(ans, heights[i] * (right - left - 1))
            st.append(right)
        return ans

85. 最大矩形 -- 84 题三维升级版

0-1 矩阵中 找全为 1 的最大子矩阵。

枚举哪一行是最底下那行 ；往上的 1 看做柱体（需要更新），即转换为不断调用 84。

class Solution:
    # 84. 柱状图中最大的矩形
    def largestRectangleArea(self, heights: List[int]) -> int:
        st = [-1]
        ans = 0
        for right, h in enumerate(heights):
            while len(st) > 1 and heights[st[-1]] >= h:
                i = st.pop()  # 矩形的高（的下标）
                left = st[-1]  # 栈顶下面那个数就是 left
                ans = max(ans, heights[i] * (right - left - 1))
            st.append(right)
        return ans

    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        n = len(matrix[0])
        heights = [0] * (n + 1)  # 末尾多一个 0
        ans = 0
        for row in matrix:
            # 计算底边为 row 的柱子高度
            for j, c in enumerate(row):
                if c == '0':
                    heights[j] = 0  # 柱子高度为 0
                else:
                    heights[j] += 1  # 柱子高度加一
            ans = max(ans, self.largestRectangleArea(heights))  # 调用 84 题代码
        return ans