【Easy-VectorDB】Faiss数据结构与索引类型

速查

索引	训练	关键参数	时间复杂度	内存压缩	召回率	首选用途
IndexFlat	无	---	O(Nd)	1×	100%	小数据基准
IndexIVF	有	nlist/nprobe	O(nprobe·Nd/nlist)	1×	高	中规模精确
IndexPQ	有	m/bits	同上+解码	32×+	中高	内存极限
IndexHNSW	无	M/efC/efS	≈O(log N)	1×	高	高召回在线
IndexLSH	无	n_bits	O(N)但桶内极少	1×	低	低维极速筛

IndexFlat

• IndexFlat系列是Faiss中最基础的索引类型，其核心是"精准检索"，即遍历数据库中所有向量，计算查询向量与每个数据库向量之间的距离，最终返回距离最近的Top-K结果。因此也被称为"暴力检索"索引。
• 根据距离度量方式，IndexFlat的三种类型：
  • IndexFlat2: 基于L2（欧式距离）度量。欧式距离计算为两个向量对应维度差值的平方和的平方根。适用于衡量向量空间中需要物理距离的场景。
  • IndexFlatIP: 基于内积度量。内积为两个向量对应维度的乘积和。在Faiss中，内积被用作相似而非距离 。IndexFlatIP返回的是内积最大的向量。
  • IndexFlatCOSINE: 基于余弦相似度度量。Faiss中余弦相似度实现：1）对所有向量进行L2归一化；2）使用内积计算相似度；3）使用负相似度作为距离，以满足按升序排序的检索逻辑。

运行效果

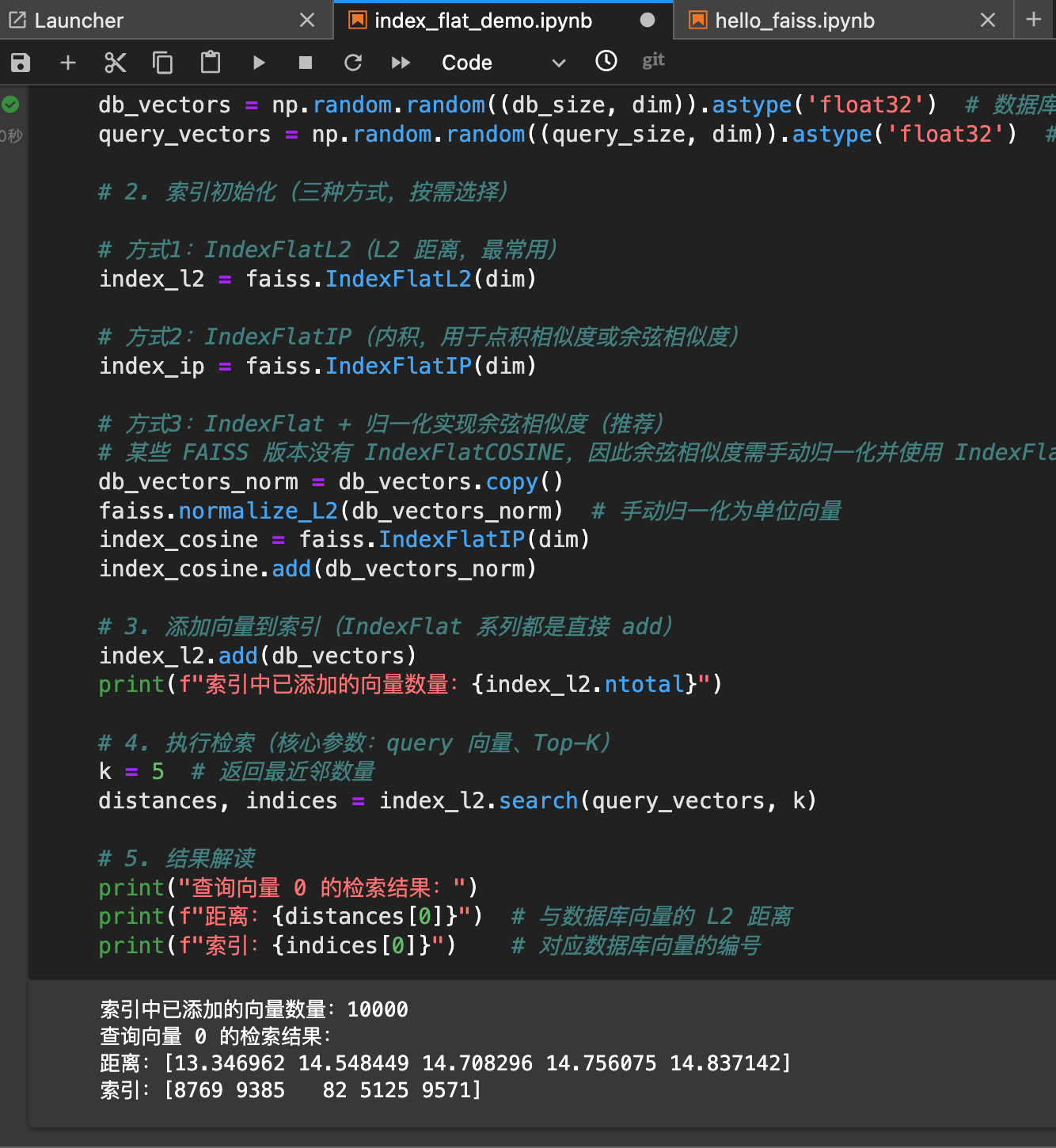
• 精准检索的性能瓶颈
  • 时间瓶颈：O(N)的线性检索复杂度；
  • 内存瓶颈：无压缩的向量存储，IndexFlat存储原始float32向量，不做压缩。float32每元素占4字节，128维向量占128x4=512字节。

实战：SIFT10k数据集精确检索对比

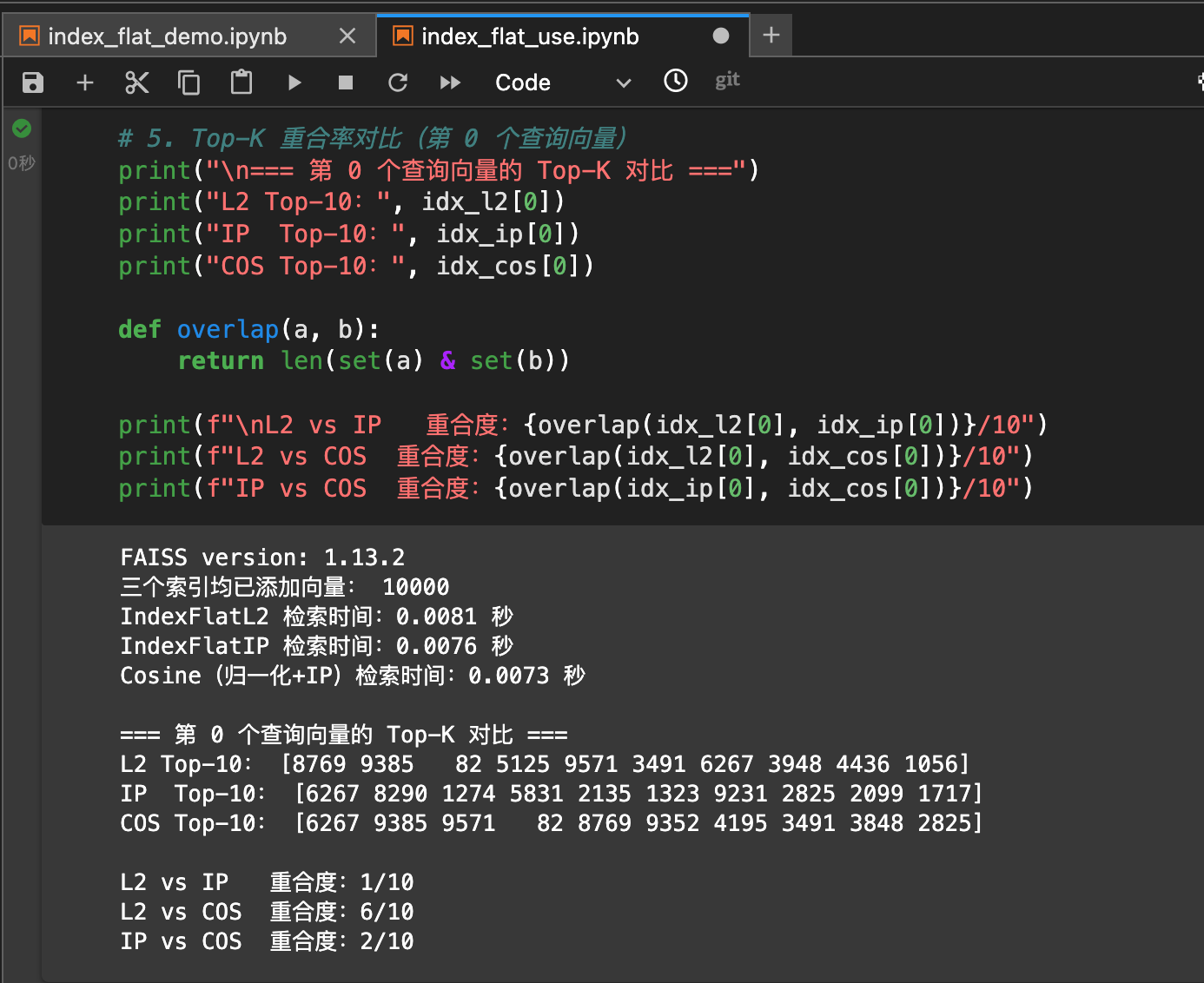
运行结论

• 不同索引检索速度差异不大。"选择索引类型"不是为了速度，而是为了"度量方式"。
• 不同距离度量会导致截然不同的检索结果。
  • L2 vs IP: 10%重合度，几乎完全不同
  • IP vs COS: 20%重合度，差别依然巨大。
  • L2 vs COS: 60%重合度，部分一致，差别仍然明显。
• 造成不同距离度量衡量是完全不同的"相似性"的原因：
  • L2: 空间位置更近
  • IP: 模长大+方向一致。方向比较一致的向量，空间位置也常常比较接近。L2和COS有较高重合度。
  • COS: 方向一致（不考虑模长）。IP受模长影响，COS不受模长影响（已归一化）。

总结 ：选择距离度量中，要选择合适的"度量方式"，才能得到合适的检索结果。

IVF系列索引

• 核心原理：倒排文件与聚类分桶
  • IVF：Faiss中用于解决大规模数据检索的核心索引类型
  • 核心思路：先聚类粪桶，再局部检索。以小（牺牲极小精度）换大（检索效率大幅提升）。
• 工作流程
  • 索引构建阶段： 聚类分桶 -> 倒排索引构建
  • 检索阶段：确定候选聚类 -> 局部精确检索。

示例: IndexIVF_FLAT- 局部精确的IVF索引

• 代码示例

示例：IndexIVF_PQ-结合PQ（乘积）量化的IVF索引

• 代码示例

IVF核心参数调优：nlist 与 nprobe的权衡

• IVF系列索引的性能（检索效率、精度）主要由nlist(聚类数) 和 nprobe(检索候选聚类数) 决定

• nlist调优逻辑： 聚类粒度与检索效率的平衡

  • nlist过大：每个聚类的向量数过少，聚类中心数量增多。
    • 优点：聚类粒度更细，查询向量与候选聚类的匹配更精准；
    • 缺点：聚类过程（训练阶段）耗时增加，且检索时需要遍历更多聚类才能保证精度（需增大nprobe)， 反而降低检索效率。
  • nlist过小：每个聚类向量数过多，聚类粒度粗糙。
    • 优点：训练速度快，检索时只需遍历少量聚类；
    • 缺点：局部检索的向量规模增大，检索效率提升有限，且聚类中心不足，可能导致精度下降。
  • nlist通常设置为数据库向量数量N的平方根附近。例如：N=10万 -> nlist=100-1000。

• nprobe调优逻辑：检索精度与效率的直接权衡点

  • nprobe增大：遍历的候选聚类更多，包含目标近邻向量的概率更高。检索精度提升，但需要计算的距离数量增加，检索延迟增大。

  • nprobe减小：遍历的候选聚类减少，检索速度更快，但可能遗漏包含目标近邻的聚类，导致精度下降。

  • 保证业务所需Recall的前提下，尽可能减小nprobe。通常先固定nlist, 通过实验测试不同nprobe对应的Recall和检索时间，选择最优值。

nprobe示例

• 示例代码
• nprobe性价比最优：从Recall 和 查询时间分析。
  • 极速场景(允许低精度)： nprobe=20, 适合对精度要求不高、追求极致速度的场景。
  • 均衡场景（精度+速度兼顾）：nprobe=50， 性价比之选。
  • 高精度场景（允许慢查询）：nprobe=100, 适合对精度要求极高（如科研、医疗），对延迟不敏感的场景。

PQ量化索引：压缩检索

• 核心原理：高维向量的"空间压缩术"
  • 三维拆解：PQ将复杂的高维向量压缩过程拆解为"拆分-量化-编码"三步骤。
    • 1）维度拆分
    • 2）子空间量化
    • 3）向量编码
• PQ索引实现：
  • IndexPQ适用于中小规模数据
  • IndexIVF_PQ结合倒排文件技术，专为大规模数据设计，是工业界最常用的方案。

IndexPQ使用步骤

• IndexPQ直接对所有向量PQ量化，核心参数包括向量维度（d)、子向量数量（m）和每个子量化器的位数（nbits)
• 示例代码

大规模优化：IndexIVF_PQ核心用法

• IndexIVF_PQ采用"粗筛选+精检索**的两级架构
  • 1）IVF层将向量分到多个聚类分区
  • 2）在目标分区内用PQ进行精确匹配。
• 示例代码

import faiss
import numpy as np
import time

# =========================
# 1. 数据准备
# =========================
d = 64          # 向量维度（需被 m 整除）
nb = 100_000     # 数据库向量数量
nq = 100        # 查询向量数量
k = 10          # Top-K 检索结果数

# 随机生成向量数据（实际使用可替换为真实向量，如 SIFT1M）
xb = np.random.random((nb, d)).astype('float32')
xq = np.random.random((nq, d)).astype('float32')

# =========================
# 2. IndexPQ 初始化与训练
# =========================
m = 8           # 子向量数量

# =========================
# 1. 核心参数配置
# =========================
nlist = 100                    # IVF 聚类分区数
param_str = f"IVF{nlist},PQ{m}"  # 索引参数字符串

# =========================
# 2. IndexIVF_PQ 初始化
# =========================
index_ivf_pq = faiss.index_factory(d, param_str, faiss.METRIC_L2)  # L2距离度量

# =========================
# 3. 训练与添加数据
# =========================
index_ivf_pq.train(xb)
index_ivf_pq.add(xb)

# 设置 nprobe（搜索分区数），平衡速度与精度
index_ivf_pq.nprobe = 10  # 搜索10个分区（推荐 nlist 的 5%-20%）

# =========================
# 4. 检索
# =========================
start = time.time()
distances_ivf, indices_ivf = index_ivf_pq.search(xq, k)
end = time.time()
print(f"IndexIVF_PQ 检索用时：{end - start:.4f} 秒")
print("IndexIVF_PQ 检索结果（前5个查询向量的前3个结果）：")
print(indices_ivf[:5, :3])

总结

• IndexPQ: 适合中小规模数据，速度较慢但精度最高
• IndexIVF_PQ: 适合大规模数据，通过IVF分区加PQ精确匹配，大幅提升速度。
• nlist与nprobe: 平衡精度与速度关键参数，nlist 约等于数据集大小平方根，nprobe 取值5%~20%

核心问题：码本训练与精度权衡

• PQ检索的核心矛盾是"压缩率"与"精度"的平衡，而码本训练质量直接决定了这种平衡的上限。

• 码本训练：量化效果的"基石"，码本是子空间聚类中心的集合，其质量取决于训练数据和过程控制。

  • 训练数据代表性：必须使用与数据库分布一致的数据（优先用全量数据库向量），否则码本无法覆盖真实数据分布，导致量化误差剧增。
  • 迭代次数控制：Faiss中K-Means聚类默认迭代20次。若数据分布复杂，可以手动增加迭代次数。
  • 空样本问题：若子空间内部分聚类中心无向量匹配，需减少子向量数量或增大码本规模。

• 压缩率计算：量化程度的"度量衡"，PQ压缩率由子向量数量(m) 和 码本位数（nbits) 共同决定。

• 精度权衡：参数调优的"核心逻辑"。精度损失源于量化误差和搜索范围限制。通过以下调优实现平衡：

  • 子向量数m: 增大m（8->16） => 精度提升（子空间更细），速度略降，压缩率降低
  • 码本位数nbits: 增大nbits（8->12）=> 精度显著提升（聚类中心更多），训练时间增加
  • IVF分区数nlist: 增大nlist（100->500） => 精度提升（分区更细），单次搜索分区速度略快，索引构建时间增加。
  • 搜索分区数nprobe: 增大nprode（10->50) => 精度大幅提升（覆盖更多相关数据），速度降低。

实战：不同索引性能比较

• 示例代码

精度优先选暴力搜索/IVF, 速度+内存优先选择IVF_PQ, 内存极度受限选择PQ。

总结

• PQ：通过"维度查费+子空间量化"压缩高维向量，可通过参数m(子向量数量) + nbits（码本位数）调节压缩率与精度。
• IndexIVF_PQ: 适用于大规模向量数据检索，nlist(聚类中心数) 和 nprobe(搜索分区数)是平衡速度与精度的关键参数。

HNSW索引：图结构近邻检索

• 核心思想：小世界网络与分层结构
  • 网络中任意两个节点之间存在短路径，同事哦结合分层策略结构构建索引。
  • 多层图结构：将向量数据集构建成多层图，上层图为"粗粒度导航层"，节点连接稀疏，用于快速跨区域跳转；下层图为"细粒度精确层"，节点连接密集，用于精准定位近邻。最底层（第0层）包含全部数据节点，是检索的最终区域。
  • 搜索六层：检索从顶层图的随机入库开始，采用"贪婪搜索"策略向查询向量的近似近邻移动，直到找到当前层的局部最优节点；随后下降到下一层，以该最优节点为新入口节点重复搜索，直至到达最底层，最终在底层的局部最优节点附近筛选出目标近邻。
• 图结构检索的核心优势
  • 高召回率：丰富的节点链接关系提供了多条导航路径，减少了因聚类划分导致的近邻遗漏问题，尤其在高维数据中表现更优。
  • 稳定性能：检索性能数据分析影响较小，对于非均匀的数据集，仍能保持稳定的搜索速度和精度。
  • 灵活可调：通过核心参数可精准控制性能权衡，既能满足低延迟的实时检索需求，也能通过参数调优达到接近精确检索的精度。

IndexHNSWFlat

• IndexHNSWFLat是Faiss中HNSW索引的基础实现，采用"扁平存储**方式（不压缩向量，保证检索精度）

• 核心参数定义与作用

  • M: 定义图中每层节点的最大出度（第0层通常为2*M)，决定节点连接的密集程度。取值范围常用8-32。M值增大，导航路径更丰富、召回率更高，但索引构建时间更长、内存占用更大、查询延迟可能增加。
  • efConstruction: 索引构建时，动态筛选邻居的候选列表大小，决定邻居选择的充分性。efConstruction增大，构建的图结构更优、检索精度更高，但索引构建时间显著增加。
  • efSearch: 查询时，每层探索的候选邻居数量，直接控制查询精度与速度。不小于查询的近邻K（常用10-200）。efSearch增大，探索范围更广、召回率更高，但查询延迟增加；高质量索引可降低对efSearch的依赖。

• HNSW vs IVF-PQ性能对比

  • 核心参数调优策略："先定结构，再优质量，最后调速度"的迭代流程：
    • 确定M值：根据数据维度选择初始值（高维数据M值取16-32，低维数据M值取8-16），以"内存占用可接受"为前提，优先保证图结构的鲁棒性。
    • 优化efConstruction: 在构建时间允许的情况下，尽可能增大efConstruction（如200-500），构建高质量索引，为后续查询优化预留空间。
    • 调整efSearch: 以"满足目标召回率"为目标，选择最小efSearch（如召回率要求0.95时，逐步增大efSearch直至达标）
    • 调参口诀：M定连接密度，efConstruction筑索引质量，efSearch控查询快慢，三者平衡是关键。
  • 硬件与工程优化
    • GPU加速：对于超大规模数据（千万级以上），使用GPU版本Faiss可将查询速度提升10-100倍，核心代码只需修改索引初始化。
    • 批量查询：将单条查询合并为批量查询（如一次查询100条），利用向量计算的并行性，降低单位查询时间。
    • 索引持久化：将构建好的索引保存到磁盘，避免重复构建，节省时间。

5LSH索引：哈希检索

• IndexLSH原理：哈希检索的核心逻辑

  • 传统哈希：最小化哈希冲突，确保不同输入映射到不同哈希值
  • LSH（局部敏感哈希）：最大化相似向量的哈希冲突，将相似的高维向量映射到同一个哈希桶中，非相似向量映射到同一桶的概率极低。

• Faiss IndexLSH的实现原理

  • 构建随机超平面：生成n_bits个随机超平面，超平面将高维空间分割成多个区域；
  • 向量哈希编码：对于每个输入向量，计算其与所有超平面法向量的点积，点积为正则编码为1，负则编码为0，最终形成一个n_bits位的二进制哈希码；
  • 桶存储与检索：将具有相同哈希码的向量归入同一桶，查询时仅需计算查询向量的哈希码，在对应桶内筛选相似向量，避免全量比对。
  • 关键：n_bits是核心参数，n_bits越大，哈希码区分度越高，检索精度越高，但哈希桶数量增长，可能导致桶内向量数量过少，反而降低效率；n_bits越小则相反。

• IndexLSH核心API解析

• IndexLSH适用场景：低维数据的高效近似检索

• IndexLSH示例

• 总结

  • LSH原理：通过随机超平面生成哈希码，将相似向量聚集到同一桶，实现快速近似检索；
  • API核心：IndexLSH(d, n_bits)初始化，add()加向量，search()做检索，n_bits()是精度与速度的调节关键；
  • 适用场景：低维、中小规模、近似检索优先的场景，如快速候选召回。

参考学习资料

Faiss数据结构与索引类型