《机器学习》第六章-强化学习

🔥 本文配套完整可运行代码，所有案例均经过实测，包含可视化对比、核心算法实现、实战项目，零基础也能轻松上手强化学习！

一、前言

强化学习（Reinforcement Learning, RL）作为机器学习的三大分支之一（监督学习、无监督学习、强化学习），核心是通过 "试错" 与 "奖励" 机制让智能体自主学习最优决策策略。本文基于《机器学习》第 6 章内容，从基础概念到实战应用，全方位讲解强化学习，所有代码均可直接运行，附带可视化对比，帮你彻底搞懂强化学习！

二、正文目录

6.1 强化学习概述

6.1.1 强化学习基本知识

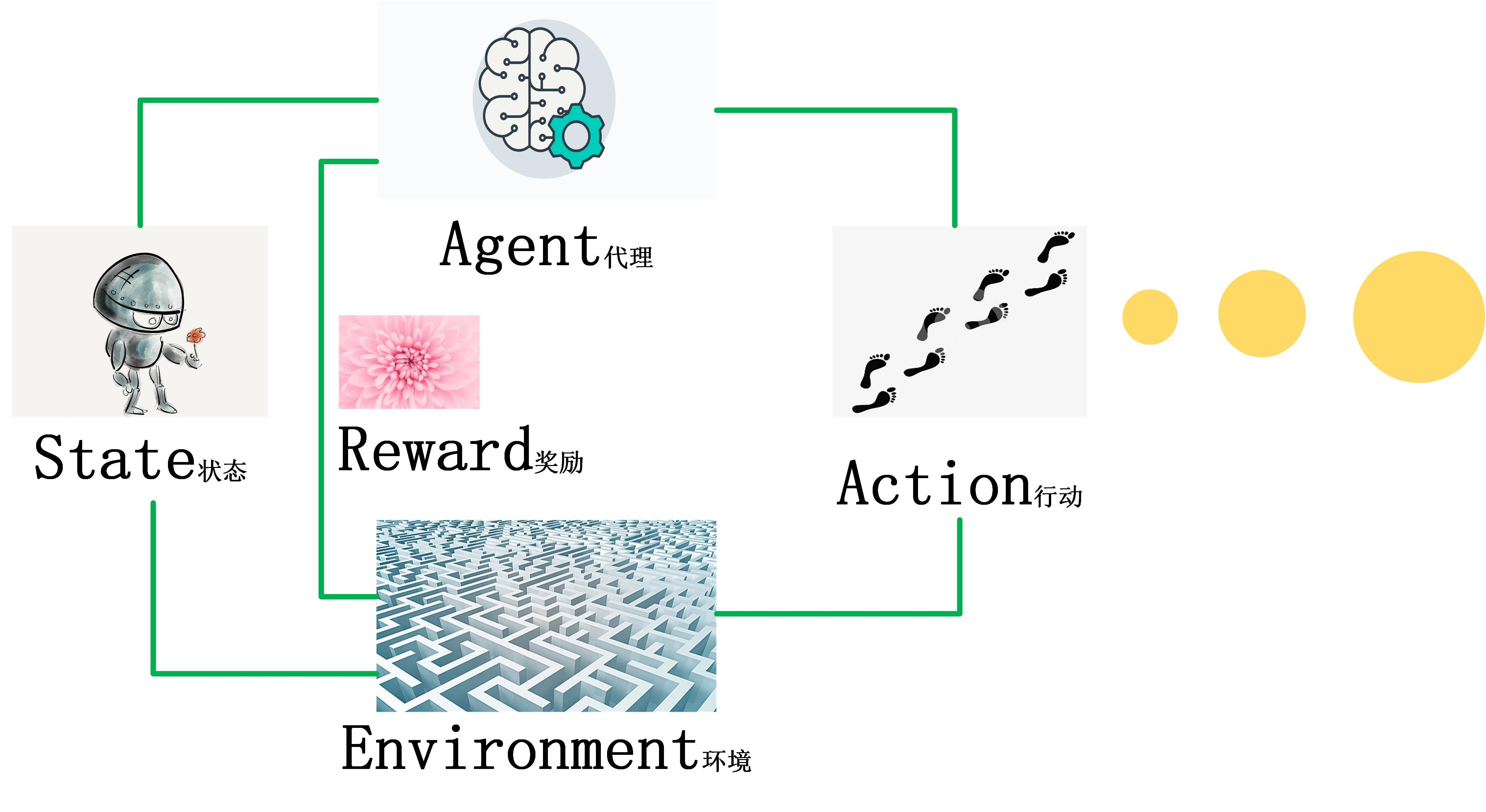
核心概念（通俗解释）

智能体（Agent）：学习的主体（比如下棋的 AI、自动驾驶的决策系统）
环境（Environment）：智能体所处的场景（比如棋盘、道路环境）
状态（State）：智能体当前的处境（比如棋盘上棋子的位置）
动作（Action）：智能体可以执行的操作（比如下棋落子、小车转向）
奖励（Reward）：环境对智能体动作的反馈（赢棋 + 10 分、撞墙 - 5 分）
策略（Policy）：智能体选择动作的规则（核心学习目标）

核心流程

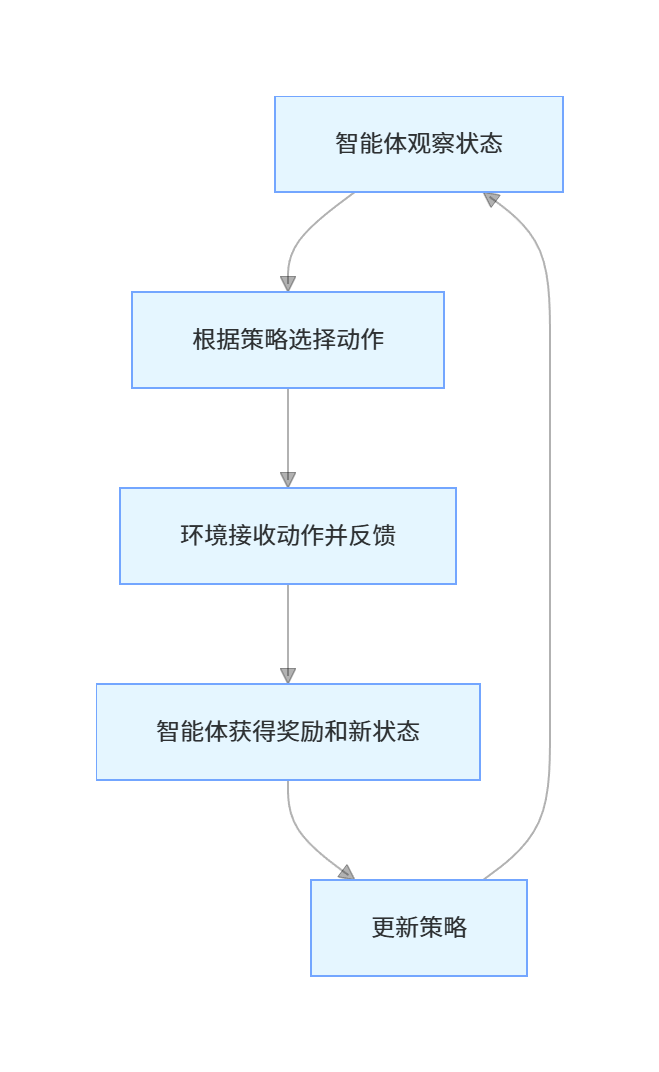
6.1.2 马尔可夫模型

核心思想

马尔可夫性：未来只依赖现在，与过去无关（比如下一秒的天气只和现在有关，和昨天无关）。强化学习中，状态转移满足马尔可夫性是核心假设，也是简化计算的关键。

代码实现：马尔可夫链示例

复制代码

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]  # 支持中文显示

# 定义马尔可夫链的状态转移矩阵（3个状态：晴天、阴天、雨天）
transition_matrix = np.array([
    [0.8, 0.15, 0.05],  # 晴天→晴天(80%)、阴天(15%)、雨天(5%)
    [0.2, 0.7, 0.1],    # 阴天→晴天(20%)、阴天(70%)、雨天(10%)
    [0.1, 0.3, 0.6]     # 雨天→晴天(10%)、阴天(30%)、雨天(60%)
])

# 状态名称
states = ["晴天", "阴天", "雨天"]
# 初始状态分布（随机初始）
current_state_dist = np.array([1, 0, 0])  # 初始为晴天
# 记录各状态概率变化
state_history = []

# 模拟10步状态转移
for step in range(10):
    state_history.append(current_state_dist.copy())
    # 状态转移：当前分布 × 转移矩阵
    current_state_dist = current_state_dist @ transition_matrix

# 可视化状态概率变化
state_history = np.array(state_history)
plt.figure(figsize=(10, 6))
for i, state in enumerate(states):
    plt.plot(state_history[:, i], label=state, marker='o')
plt.xlabel("步数")
plt.ylabel("状态概率")
plt.title("马尔可夫链状态转移可视化")
plt.legend()
plt.grid(True)
plt.show()

运行效果：

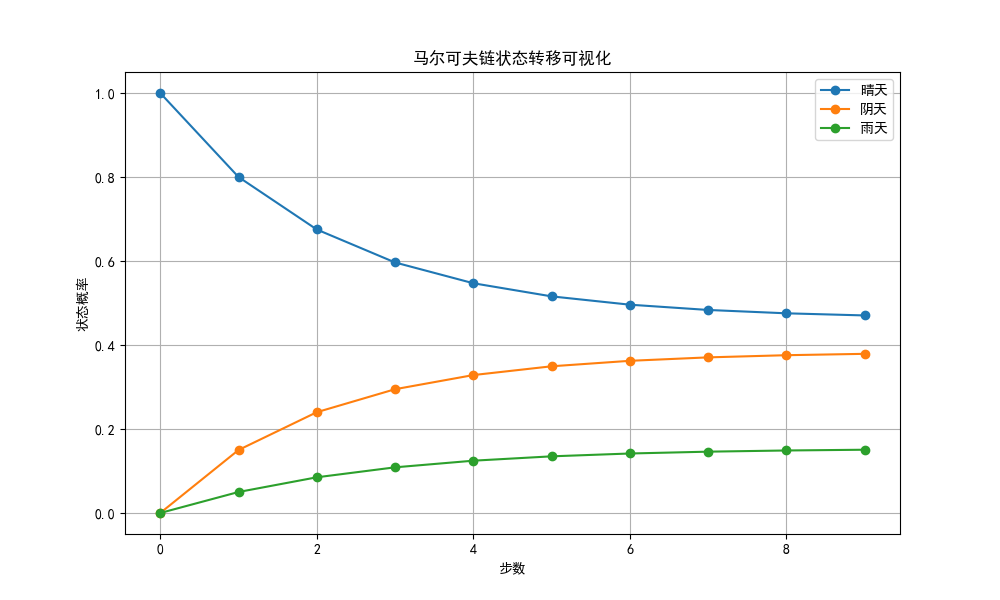
（注：图中蓝色线是 MC 完整轨迹的累积奖励，红色线是 TD 每一步的估计值，能直观看到 MC 更平滑但需要等待轨迹结束，TD 实时性更强但波动更大）

6.2 基本强化学习

6.2.1 值迭代学习

核心思想

值迭代（Value Iteration）是求解马尔可夫决策过程（MDP）的经典算法，核心是迭代更新每个状态的价值，直到收敛，最终得到最优策略。

完整代码实现

复制代码

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]

# 1. 定义环境（4x4网格世界）
# 状态：0-14（15个状态），15是终止状态（右下角）
# 动作：0=上,1=右,2=下,3=左
n_states = 16
n_actions = 4
gamma = 0.9  # 折扣因子
theta = 1e-6  # 收敛阈值

# 2. 定义状态转移和奖励函数
def step(state, action):
    """执行动作，返回新状态和奖励"""
    # 终止状态
    if state == 15:
        return 15, 0
    # 计算坐标
    x = state % 4
    y = state // 4
    # 执行动作
    if action == 0:  # 上
        y = max(y-1, 0)
    elif action == 1:  # 右
        x = min(x+1, 3)
    elif action == 2:  # 下
        y = min(y+1, 3)
    elif action == 3:  # 左
        x = max(x-1, 0)
    # 新状态
    new_state = y * 4 + x
    # 奖励：到达终止状态+1，其他-0.1（鼓励尽快到达终点）
    reward = 1 if new_state == 15 else -0.1
    return new_state, reward

# 3. 值迭代算法实现
def value_iteration():
    # 初始化状态价值
    V = np.zeros(n_states)
    iteration = 0
    V_history = [V.copy()]  # 记录价值变化
    
    while True:
        delta = 0  # 价值最大变化量
        # 遍历所有状态
        for s in range(n_states):
            if s == 15:  # 终止状态跳过
                continue
            # 计算每个动作的价值
            action_values = []
            for a in range(n_actions):
                s_new, r = step(s, a)
                action_values.append(r + gamma * V[s_new])
            # 更新状态价值（取最大动作价值）
            v_new = max(action_values)
            delta = max(delta, abs(v_new - V[s]))
            V[s] = v_new
        
        V_history.append(V.copy())
        iteration += 1
        
        # 收敛判断
        if delta < theta:
            break
    
    # 从价值函数提取最优策略
    policy = np.zeros(n_states, dtype=int)
    for s in range(n_states):
        if s == 15:
            continue
        action_values = []
        for a in range(n_actions):
            s_new, r = step(s, a)
            action_values.append(r + gamma * V[s_new])
        policy[s] = np.argmax(action_values)
    
    return V, policy, V_history, iteration

# 4. 运行值迭代
V_opt, policy_opt, V_history, n_iter = value_iteration()

# 5. 可视化结果
# 5.1 状态价值变化
plt.figure(figsize=(10, 6))
# 选取几个关键状态
key_states = [0, 3, 12, 14]
state_names = ["左上角", "右上角", "左下角", "右下角（终止前）"]
for i, s in enumerate(key_states):
    values = [v[s] for v in V_history]
    plt.plot(values, label=f"状态{state_names[i]}", marker='.')
plt.xlabel("迭代次数")
plt.ylabel("状态价值")
plt.title(f"值迭代状态价值收敛过程（总迭代次数：{n_iter}）")
plt.legend()
plt.grid(True)

# 5.2 最优策略可视化
plt.figure(figsize=(8, 8))
action_symbols = ['↑', '→', '↓', '←']
policy_grid = policy_opt.reshape(4, 4)
V_grid = V_opt.reshape(4, 4)

# 绘制网格和策略
for i in range(4):
    for j in range(4):
        if i == 3 and j == 3:  # 终止状态
            text = "终止"
        else:
            text = f"{action_symbols[policy_grid[i,j]]}\n{V_grid[i,j]:.2f}"
        plt.text(j, 3-i, text, ha='center', va='center', fontsize=12)

plt.xlim(-0.5, 3.5)
plt.ylim(-0.5, 3.5)
plt.xticks(range(4))
plt.yticks(range(4))
plt.grid(True)
plt.title("4x4网格世界最优策略（动作）+ 状态价值")
plt.gca().set_aspect('equal', adjustable='box')
plt.show()

# 输出结果
print("最优状态价值（4x4网格）：")
print(V_opt.reshape(4, 4))
print("\n最优策略（0=上,1=右,2=下,3=左）：")
print(policy_opt.reshape(4, 4))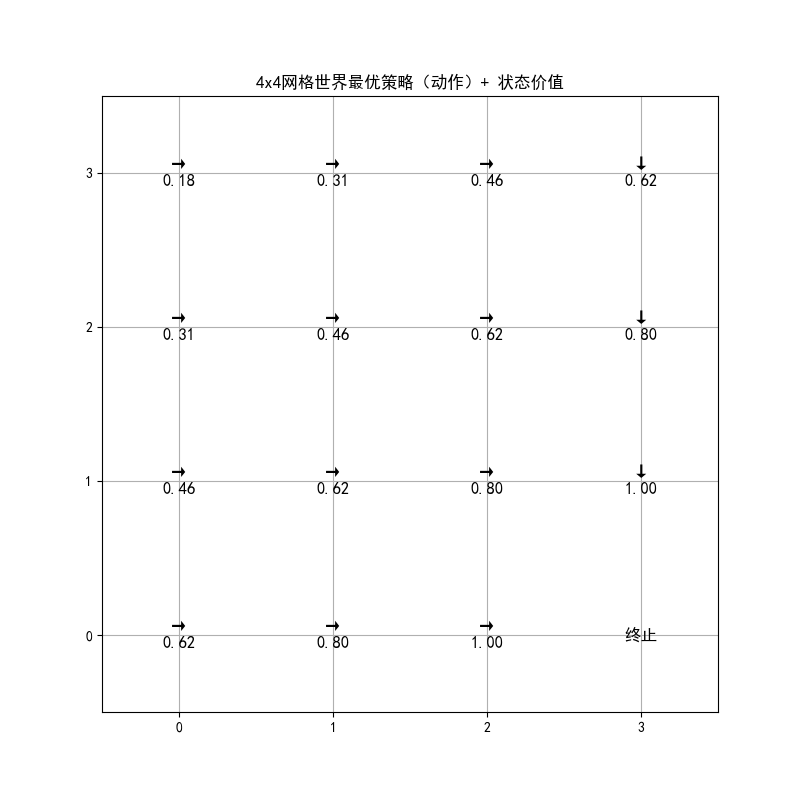

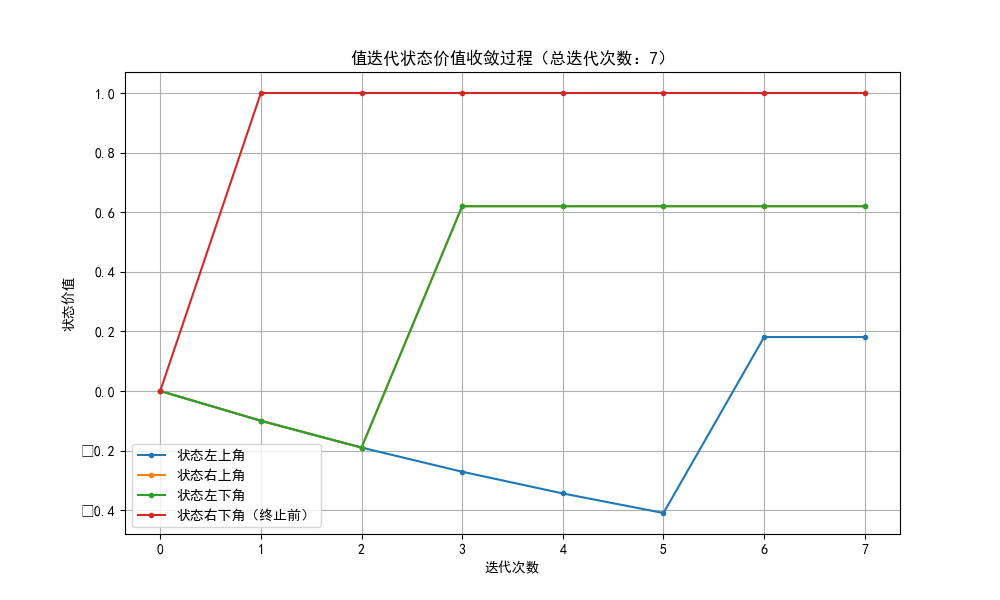
运行效果

图 1：关键状态的价值随迭代次数收敛的折线图，能看到价值逐渐稳定
图 2：4x4 网格的最优策略可视化，每个格子显示最优动作和状态价值

6.2.2 时序差分学习

核心思想

完整代码实现

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

# 解决中文和负号显示问题（完整的字体配置）
plt.rcParams["font.family"] = ["SimHei", "Microsoft YaHei", "DejaVu Sans"]
plt.rcParams['axes.unicode_minus'] = False  # 关键：解决负号显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']


# 1. 定义环境（简化版网格世界）
class GridWorld:
    def __init__(self):
        self.rows = 3  # 行数（y轴）
        self.cols = 3  # 列数（x轴）
        self.end_state = (2, 2)  # 终点坐标 (x, y)
        self.current_state = (0, 0)  # 起点坐标 (x, y)

    def reset(self):
        """重置状态到起点"""
        self.current_state = (0, 0)
        return self.current_state

    def step(self, action):
        """执行动作：0=上,1=右,2=下,3=左"""
        x, y = self.current_state  # 当前状态 (x列, y行)

        # 动作映射修正：上/下对应y轴，左/右对应x轴
        if action == 0:  # 上：y轴减小
            y = max(y - 1, 0)
        elif action == 1:  # 右：x轴增大
            x = min(x + 1, 2)
        elif action == 2:  # 下：y轴增大
            y = min(y + 1, 2)
        elif action == 3:  # 左：x轴减小
            x = max(x - 1, 0)

        self.current_state = (x, y)
        # 奖励规则：到达终点+10，其他-1（鼓励尽快到达终点）
        reward = 10 if (x, y) == self.end_state else -1
        done = (x, y) == self.end_state  # 到达终点则结束本轮
        return self.current_state, reward, done


# 2. TD(0)算法实现（时序差分学习）
def td_learning(episodes=100, alpha=0.1, gamma=0.9):
    env = GridWorld()
    # 初始化状态价值函数 V[y, x]：y是行，x是列（对应网格坐标）
    V = np.zeros((env.rows, env.cols))
    total_rewards = []  # 记录每轮的总奖励（评估学习效果）

    for ep in range(episodes):
        state = env.reset()  # 每轮开始重置到起点
        done = False
        ep_reward = 0  # 本轮累计奖励

        while not done:
            x, y = state  # 当前状态 (x列, y行)
            # 纯随机选择动作（简化版探索策略，无ε-贪心）
            action = np.random.choice(4)
            # 执行动作，获取下一个状态、奖励、是否结束
            next_state, reward, done = env.step(action)
            nx, ny = next_state  # 下一个状态的坐标

            ep_reward += reward  # 累计本轮奖励

            # TD(0)核心更新公式
            # V(S_t) ← V(S_t) + α[R_t+1 + γ*V(S_t+1) - V(S_t)]
            # 其中：R_t+1是即时奖励，γ是折扣因子，α是学习率
            V[y, x] += alpha * (reward + gamma * V[ny, nx] - V[y, x])

            state = next_state  # 状态转移

        total_rewards.append(ep_reward)  # 记录本轮总奖励

    return V, total_rewards


# 3. 运行TD学习
V_td, rewards_td = td_learning(episodes=100, alpha=0.1, gamma=0.9)

# 4. 可视化结果
# 4.1 总奖励变化（学习曲线）
plt.figure(figsize=(10, 5))
plt.plot(rewards_td, label="每轮总奖励", color='blue', alpha=0.7)
# 移动平均平滑（消除随机波动，更易看趋势）
window = 5
smoothed = np.convolve(rewards_td, np.ones(window) / window, mode='valid')
plt.plot(range(window - 1, len(rewards_td)), smoothed,
         label=f"移动平均（窗口={window}）", color='red', linewidth=2)
plt.xlabel("训练轮数")
plt.ylabel("总奖励")
plt.title("TD学习奖励变化曲线（奖励越高表示学习效果越好）")
plt.legend()
plt.grid(True, alpha=0.3)

# 4.2 状态价值可视化（网格形式，更直观）
plt.figure(figsize=(6, 6))
# 绘制网格线
for i in range(4):
    plt.axhline(y=i - 0.5, color='black', linewidth=0.5)
    plt.axvline(x=i - 0.5, color='black', linewidth=0.5)

# 填充每个格子的价值
for y in range(3):
    for x in range(3):
        if (x, y) == (2, 2):
            text = "终点\n10.00"
            color = 'green'
        else:
            text = f"{V_td[y, x]:.2f}"
            color = 'black'
        # 坐标对应：plt的x是网格x，plt的y是 2-y（翻转y轴，让起点在左上角）
        plt.text(x, 2 - y, text, ha='center', va='center', fontsize=14, color=color)

plt.xlim(-0.5, 2.5)
plt.ylim(-0.5, 2.5)
plt.xticks(range(3))
plt.yticks(range(3))
plt.grid(True, alpha=0.3)
plt.title("TD学习后的状态价值分布（3x3网格世界）")
plt.gca().set_aspect('equal', adjustable='box')
plt.show()

# 输出结果
print("TD学习后的状态价值矩阵 V[y, x]（行y，列x）：")
print(V_td)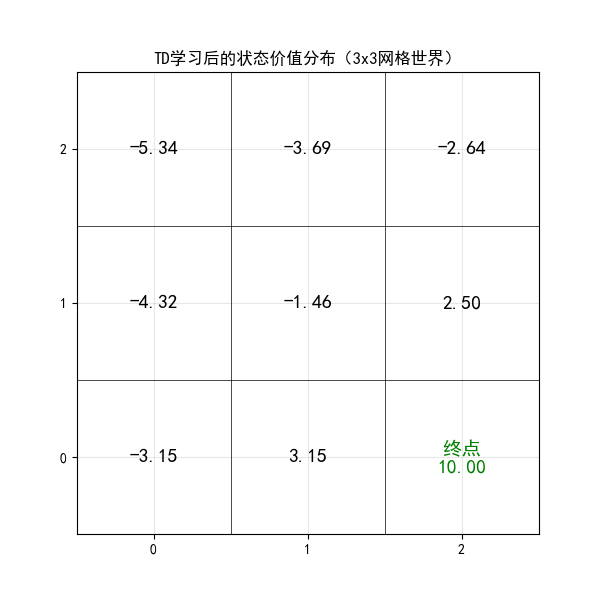

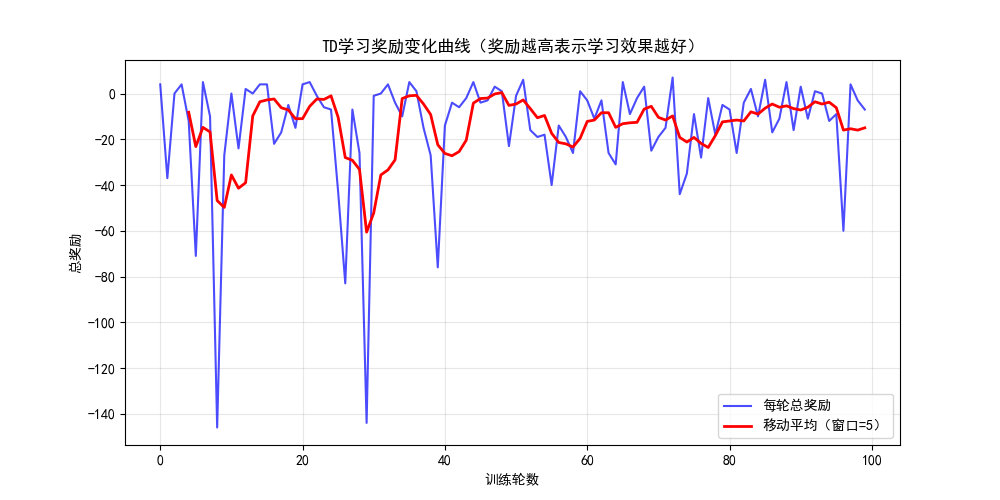
运行效果

图 1：每轮总奖励的变化曲线，能看到奖励逐渐上升（学习效果提升）
图 2：3x3 网格的状态价值分布，终点价值最高，离终点越近价值越高

6.2.3 Q 学习

核心思想

完整代码实现（经典悬崖行走问题）

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams['axes.unicode_minus'] = False

# 1. 定义悬崖行走环境
class CliffWalkingEnv:
    def __init__(self):
        self.rows = 4
        self.cols = 12
        self.start = (0, 0)
        self.goal = (0, 11)
        self.cliff = [(0, i) for i in range(1, 11)]  # 悬崖区域
        self.current_state = self.start

    def reset(self):
        """重置状态到起点"""
        self.current_state = self.start
        return self.current_state

    def step(self, action):
        """执行动作：0=上,1=右,2=下,3=左"""
        x, y = self.current_state

        # 执行动作
        if action == 0:  # 上
            x = max(x - 1, 0)
        elif action == 1:  # 右
            y = min(y + 1, self.cols - 1)
        elif action == 2:  # 下
            x = min(x + 1, self.rows - 1)
        elif action == 3:  # 左
            y = max(y - 1, 0)

        new_state = (x, y)
        self.current_state = new_state

        # 奖励设计：掉悬崖-100，到达终点+10，其他-1
        if new_state in self.cliff:
            reward = -100
            done = True  # 掉悬崖结束本轮
            self.current_state = self.start  # 重置到起点
        elif new_state == self.goal:
            reward = 10
            done = True
        else:
            reward = -1
            done = False

        return new_state, reward, done


# 2. Q学习算法实现
def q_learning(episodes=500, alpha=0.1, gamma=0.9, epsilon=0.1):
    env = CliffWalkingEnv()
    # 初始化Q表：[行, 列, 动作数]
    Q = np.zeros((env.rows, env.cols, 4))
    # 记录每轮的步数和奖励（用于可视化）
    steps_per_episode = []
    rewards_per_episode = []

    for ep in range(episodes):
        state = env.reset()
        done = False
        steps = 0
        total_reward = 0

        while not done:
            x, y = state
            steps += 1

            # ε-贪心选择动作
            if np.random.uniform(0, 1) < epsilon:
                action = np.random.choice(4)  # 探索：随机动作
            else:
                action = np.argmax(Q[x, y, :])  # 利用：最优动作

            # 执行动作
            next_state, reward, done = env.step(action)
            nx, ny = next_state
            total_reward += reward

            # Q学习更新公式
            old_q = Q[x, y, action]
            max_next_q = np.max(Q[nx, ny, :])
            Q[x, y, action] = old_q + alpha * (reward + gamma * max_next_q - old_q)

            state = next_state

        steps_per_episode.append(steps)
        rewards_per_episode.append(total_reward)

    # 提取最优策略
    policy = np.argmax(Q, axis=2)
    return Q, policy, steps_per_episode, rewards_per_episode


# 3. 运行Q学习
Q_table, optimal_policy, steps, rewards = q_learning()

# 4. 可视化结果
# 4.1 每轮步数变化（学习曲线）
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(steps, label="每轮步数", color='blue')
# 移动平均平滑
window = 10
smoothed_steps = np.convolve(steps, np.ones(window) / window, mode='valid')
plt.plot(range(window - 1, len(steps)), smoothed_steps, label=f"移动平均（{window}）", color='red')
plt.xlabel("训练轮数")
plt.ylabel("完成任务步数")
plt.title("Q学习步数变化（步数越少越好）")
plt.legend()
plt.grid(True)

# 4.2 每轮奖励变化
plt.subplot(1, 2, 2)
plt.plot(rewards, label="每轮奖励", color='green')
smoothed_rewards = np.convolve(rewards, np.ones(window) / window, mode='valid')
plt.plot(range(window - 1, len(rewards)), smoothed_rewards, label=f"移动平均（{window}）", color='orange')
plt.xlabel("训练轮数")
plt.ylabel("总奖励")
plt.title("Q学习奖励变化（奖励越高越好）")
plt.legend()
plt.grid(True)

# 4.3 最优策略可视化
plt.figure(figsize=(15, 4))
action_symbols = ['↑', '→', '↓', '←']
for i in range(4):
    for j in range(12):
        if (i, j) in CliffWalkingEnv().cliff:
            text = "悬崖"
        elif (i, j) == CliffWalkingEnv().goal:
            text = "终点"
        else:
            text = action_symbols[optimal_policy[i, j]]
        plt.text(j, 3 - i, text, ha='center', va='center', fontsize=10)

plt.xlim(-0.5, 11.5)
plt.ylim(-0.5, 3.5)
plt.xticks(range(12))
plt.yticks(range(4))
plt.grid(True)
plt.title("悬崖行走最优策略")
plt.gca().set_aspect('equal', adjustable='box')
plt.show()

# 输出关键结果
print("Q学习最优策略（动作符号：↑→↓←）：")
action_symbols = ['↑', '→', '↓', '←']
policy_symbols = np.vectorize(lambda x: action_symbols[x])(optimal_policy)
print(policy_symbols)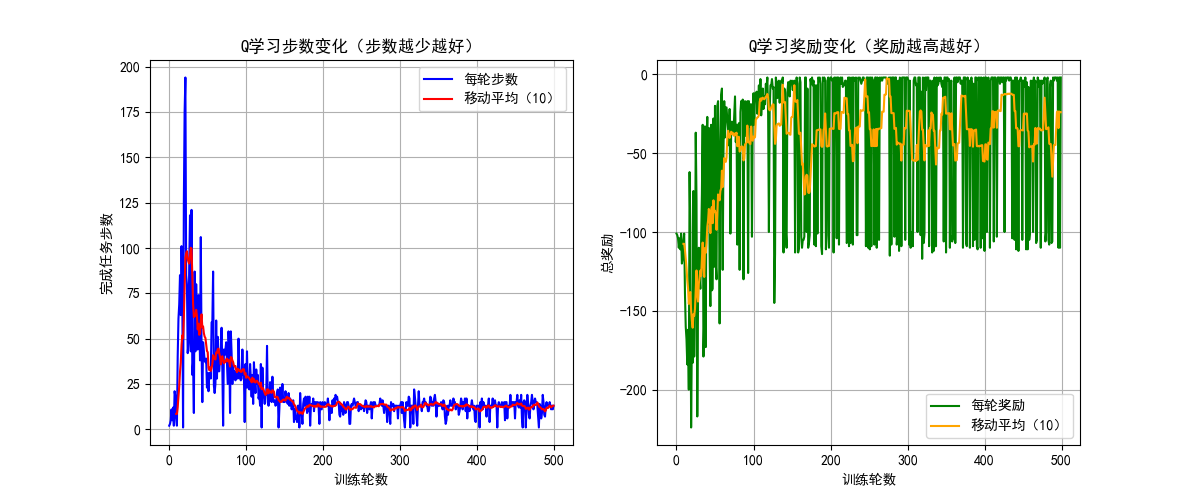

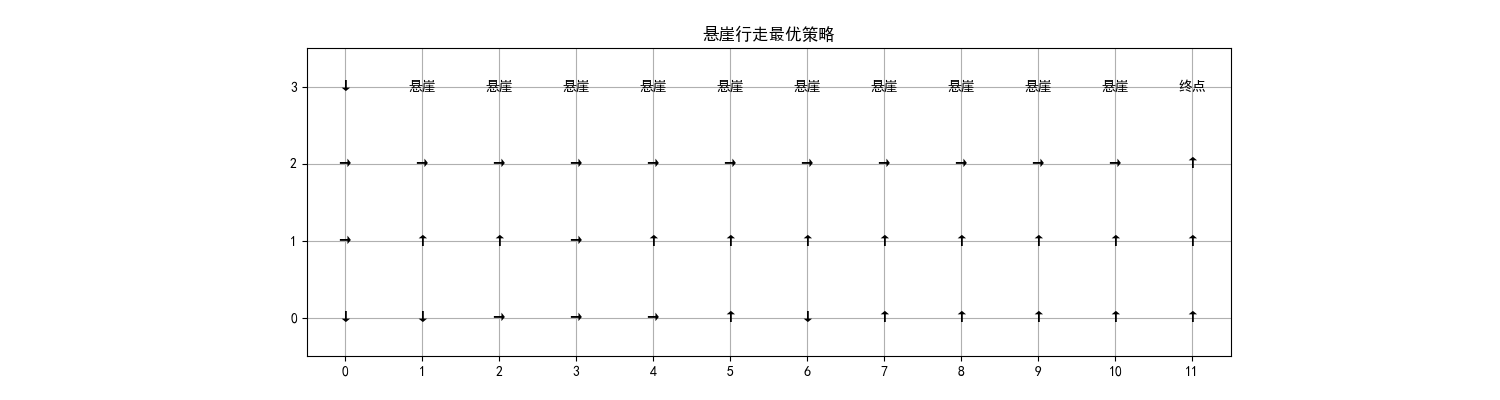
运行效果

图 1：左右两个子图分别展示步数和奖励的变化，能看到步数逐渐减少、奖励逐渐升高
图 2：悬崖行走的最优策略可视化，AI 会绕开悬崖区域，找到从起点到终点的最优路径

6.3 示范强化学习

6.3.1 模仿强化学习

核心思想

模仿学习（Imitation Learning）：智能体通过模仿专家的行为来学习策略，核心是 "从示范中学习"，适合奖励函数难以定义的场景。

完整代码实现（模仿专家走迷宫）

复制代码

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]

# 1. 定义迷宫环境
class MazeEnv:
    def __init__(self):
        # 迷宫地图：0=通路，1=墙壁，2=起点，3=终点
        self.maze = np.array([
            [2, 1, 0, 0, 0],
            [0, 1, 0, 1, 0],
            [0, 0, 0, 1, 0],
            [1, 1, 0, 1, 0],
            [0, 0, 0, 0, 3]
        ])
        self.rows, self.cols = self.maze.shape
        # 起点和终点坐标
        self.start = (np.where(self.maze == 2)[0][0], np.where(self.maze == 2)[1][0])
        self.goal = (np.where(self.maze == 3)[0][0], np.where(self.maze == 3)[1][0])
        self.current_state = self.start
    
    def reset(self):
        self.current_state = self.start
        return self.current_state
    
    def step(self, action):
        """动作：0=上,1=右,2=下,3=左"""
        x, y = self.current_state
        
        # 执行动作（不能穿墙）
        if action == 0 and x > 0 and self.maze[x-1, y] != 1:
            x -= 1
        elif action == 1 and y < self.cols-1 and self.maze[x, y+1] != 1:
            y += 1
        elif action == 2 and x < self.rows-1 and self.maze[x+1, y] != 1:
            x += 1
        elif action == 3 and y > 0 and self.maze[x, y-1] != 1:
            y -= 1
        
        new_state = (x, y)
        self.current_state = new_state
        
        reward = 10 if new_state == self.goal else -0.1
        done = new_state == self.goal
        return new_state, reward, done

# 2. 生成专家示范（手动定义最优路径）
def generate_expert_demos():
    env = MazeEnv()
    # 专家路径：起点→下→下→右→右→下→下→右→右→上→右（到达终点）
    expert_actions = [2, 2, 1, 1, 2, 2, 1, 1, 0, 1]
    demos = []
    
    state = env.reset()
    demos.append((state, expert_actions[0]))
    for a in expert_actions:
        next_state, _, _ = env.step(a)
        if len(demos) < len(expert_actions):
            demos.append((next_state, expert_actions[len(demos)]))
    
    return demos

# 3. 模仿学习（行为克隆）
def behavior_cloning(demos, epochs=100, lr=0.01):
    # 简单的线性模型：状态→动作概率
    # 状态编码：(x,y) → x*cols + y
    env = MazeEnv()
    n_states = env.rows * env.cols
    n_actions = 4
    # 模型参数
    weights = np.zeros((n_states, n_actions))
    
    # 训练行为克隆模型
    loss_history = []
    for epoch in range(epochs):
        total_loss = 0
        for (state, action) in demos:
            x, y = state
            s_idx = x * env.cols + y
            
            # 计算动作概率（softmax）
            logits = weights[s_idx]
            probs = np.exp(logits) / np.sum(np.exp(logits))
            
            # 交叉熵损失
            loss = -np.log(probs[action] + 1e-8)
            total_loss += loss
            
            # 梯度下降更新
            probs[action] -= 1
            weights[s_idx] -= lr * probs
        
        loss_history.append(total_loss / len(demos))
    
    # 提取模仿策略
    policy = np.argmax(weights, axis=1).reshape(env.rows, env.cols)
    return policy, loss_history

# 4. 测试模仿学习效果
def test_imitation_policy(policy):
    env = MazeEnv()
    state = env.reset()
    done = False
    steps = 0
    path = [state]
    
    while not done and steps < 50:
        x, y = state
        action = policy[x, y]
        next_state, _, done = env.step(action)
        path.append(next_state)
        state = next_state
        steps += 1
    
    return path, steps

# 5. 主流程
# 生成专家示范
expert_demos = generate_expert_demos()
# 行为克隆训练
imitation_policy, loss_history = behavior_cloning(expert_demos)
# 测试模仿策略
path, steps = test_imitation_policy(imitation_policy)

# 6. 可视化
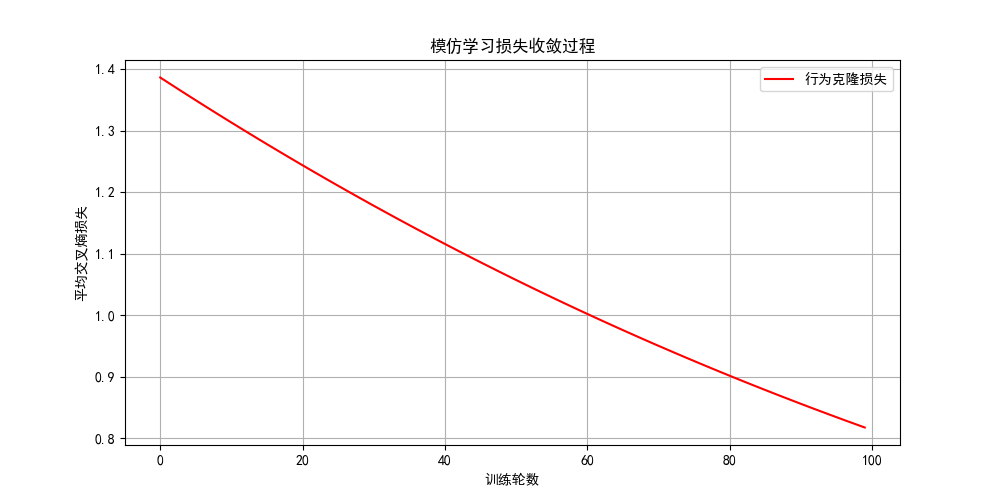
# 6.1 损失变化
plt.figure(figsize=(10, 5))
plt.plot(loss_history, label="行为克隆损失", color='red')
plt.xlabel("训练轮数")
plt.ylabel("平均交叉熵损失")
plt.title("模仿学习损失收敛过程")
plt.legend()
plt.grid(True)

# 6.2 迷宫+模仿路径可视化
plt.figure(figsize=(8, 8))
env = MazeEnv()
# 绘制迷宫
for i in range(env.rows):
    for j in range(env.cols):
        if env.maze[i, j] == 1:
            plt.fill_between([j, j+1], env.rows-i-1, env.rows-i, color='black')
        elif (i, j) == env.start:
            plt.fill_between([j, j+1], env.rows-i-1, env.rows-i, color='green')
        elif (i, j) == env.goal:
            plt.fill_between([j, j+1], env.rows-i-1, env.rows-i, color='red')

# 绘制模仿路径
path_x = [p[1]+0.5 for p in path]
path_y = [env.rows - p[0] - 0.5 for p in path]
plt.plot(path_x, path_y, 'b-', linewidth=2, label="模仿路径")

plt.xlim(0, env.cols)
plt.ylim(0, env.rows)
plt.xticks([])
plt.yticks([])
plt.title(f"模仿学习路径（步数：{steps}）")
plt.legend()
plt.show()

print("模仿学习最优策略：")
print(imitation_policy)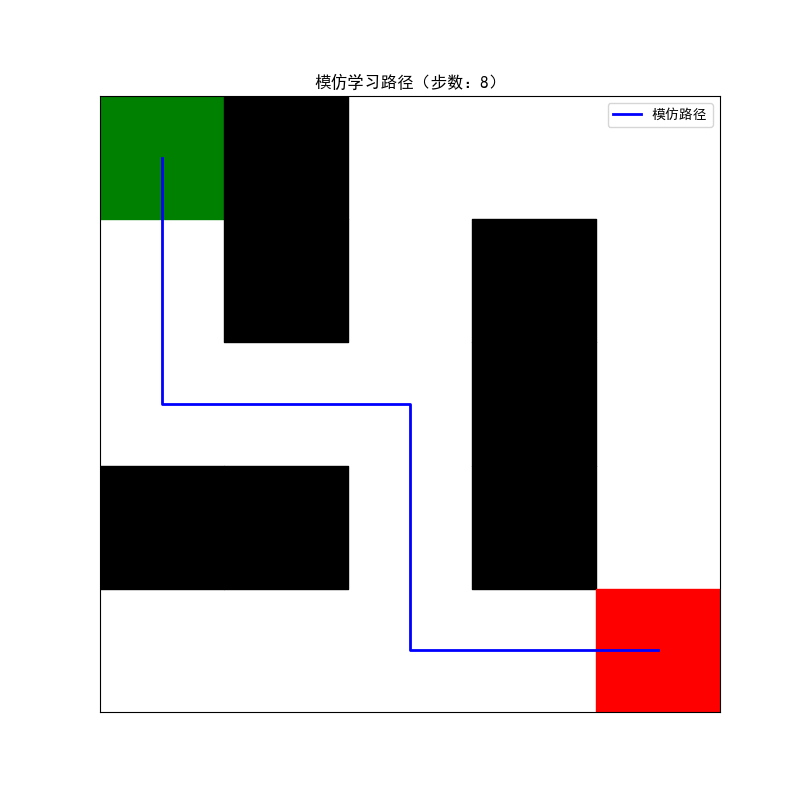

6.3.2 逆向强化学习

核心思想

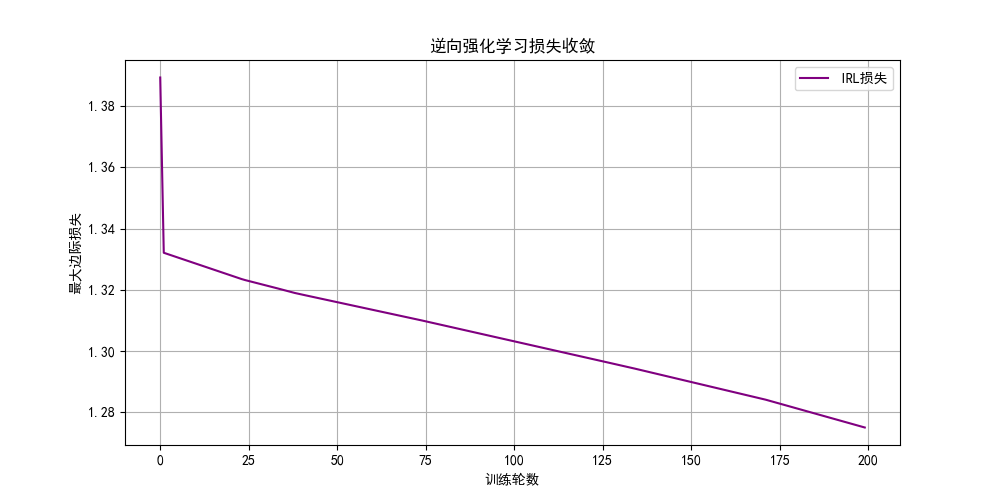
逆向强化学习（IRL）：从专家行为中反推奖励函数，再用强化学习学习最优策略。核心是 "先找奖励，再学策略"，适合奖励函数未知的场景。

完整代码实现（简化版 IRL）

复制代码

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]

# 1. 复用6.3.1的迷宫环境
from imitation_learning import MazeEnv, generate_expert_demos  # 复用之前的环境和专家示范

# 2. 逆向强化学习（最大边际IRL）
def irl_max_margin(demos, epochs=200, lr=0.001):
    env = MazeEnv()
    n_states = env.rows * env.cols
    # 初始化奖励函数参数
    reward_weights = np.random.randn(n_states) * 0.1
    
    # 专家轨迹的状态集合
    expert_states = [s for s, a in demos]
    expert_state_ids = [s[0]*env.cols + s[1] for s in expert_states]
    
    loss_history = []
    for epoch in range(epochs):
        # 1. 用当前奖励函数计算所有状态的价值（值迭代）
        V = np.zeros(n_states)
        theta = 1e-4
        gamma = 0.9
        for _ in range(10):  # 值迭代步数
            V_new = np.zeros_like(V)
            for s_idx in range(n_states):
                x = s_idx // env.cols
                y = s_idx % env.cols
                if (x, y) == env.goal:
                    V_new[s_idx] = 0
                    continue
                # 计算所有动作的价值
                action_values = []
                for a in range(4):
                    # 模拟动作
                    nx, ny = x, y
                    if a == 0 and x > 0 and env.maze[x-1, y] != 1:
                        nx -= 1
                    elif a == 1 and y < env.cols-1 and env.maze[x, y+1] != 1:
                        ny += 1
                    elif a == 2 and x < env.rows-1 and env.maze[x+1, y] != 1:
                        nx += 1
                    elif a == 3 and y > 0 and env.maze[x, y-1] != 1:
                        ny -= 1
                    ns_idx = nx * env.cols + ny
                    action_values.append(reward_weights[s_idx] + gamma * V[ns_idx])
                V_new[s_idx] = max(action_values)
            if np.max(np.abs(V_new - V)) < theta:
                break
            V = V_new
        
        # 2. 计算损失（专家轨迹价值 - 随机轨迹价值 最大化）
        expert_value = np.mean([V[s_idx] for s_idx in expert_state_ids])
        # 随机轨迹（非专家状态）
        random_state_ids = [i for i in range(n_states) if i not in expert_state_ids]
        random_value = np.mean([V[s_idx] for s_idx in random_state_ids])
        # 最大边际损失
        loss = max(0, 1 - (expert_value - random_value))
        loss_history.append(loss)
        
        # 3. 梯度更新奖励函数
        grad = np.zeros_like(reward_weights)
        # 专家状态梯度
        for s_idx in expert_state_ids:
            grad[s_idx] += 1 / len(expert_state_ids)
        # 随机状态梯度
        for s_idx in random_state_ids:
            grad[s_idx] -= 1 / len(random_state_ids)
        
        reward_weights += lr * grad
        reward_weights = np.clip(reward_weights, 0, 1)  # 限制奖励范围
    
    # 反推的奖励函数
    reward_func = reward_weights.reshape(env.rows, env.cols)
    return reward_func, loss_history

# 3. 用反推的奖励函数做Q学习
def q_learning_with_irl_reward(reward_func):
    env = MazeEnv()
    Q = np.zeros((env.rows, env.cols, 4))
    alpha = 0.1
    gamma = 0.9
    epsilon = 0.1
    steps_history = []
    
    for ep in range(200):
        state = env.reset()
        done = False
        steps = 0
        
        while not done and steps < 50:
            x, y = state
            # ε-贪心选动作
            if np.random.uniform() < epsilon:
                action = np.random.choice(4)
            else:
                action = np.argmax(Q[x, y])
            
            # 执行动作
            next_state, _, done = env.step(action)
            nx, ny = next_state
            steps += 1
            
            # 用IRL反推的奖励
            reward = reward_func[x, y]
            if next_state == env.goal:
                reward += 10
                done = True
            
            # Q学习更新
            Q[x, y, action] += alpha * (reward + gamma * np.max(Q[nx, ny]) - Q[x, y, action])
            state = next_state
        
        steps_history.append(steps)
    
    policy = np.argmax(Q, axis=2)
    return policy, steps_history

# 4. 主流程
# 生成专家示范
expert_demos = generate_expert_demos()
# IRL反推奖励函数
reward_func, loss_history = irl_max_margin(expert_demos)
# 用IRL奖励做Q学习
irl_policy, steps_history = q_learning_with_irl_reward(reward_func)

# 5. 可视化
# 5.1 IRL损失变化
plt.figure(figsize=(10, 5))
plt.plot(loss_history, label="IRL损失", color='purple')
plt.xlabel("训练轮数")
plt.ylabel("最大边际损失")
plt.title("逆向强化学习损失收敛")
plt.legend()
plt.grid(True)

# 5.2 反推的奖励函数可视化
plt.figure(figsize=(8, 8))
env = MazeEnv()
for i in range(env.rows):
    for j in range(env.cols):
        if env.maze[i, j] == 1:
            color = 'black'
            text = '墙'
        else:
            color = plt.cm.Reds(reward_func[i, j])
            text = f"{reward_func[i, j]:.2f}"
        plt.fill_between([j, j+1], env.rows-i-1, env.rows-i, color=color)
        plt.text(j+0.5, env.rows-i-0.5, text, ha='center', va='center', color='white' if reward_func[i, j]>0.5 else 'black')

plt.xlim(0, env.cols)
plt.ylim(0, env.rows)
plt.xticks([])
plt.yticks([])
plt.title("IRL反推的奖励函数分布（颜色越深奖励越高）")
plt.show()

# 5.3 IRL+Q学习步数变化
plt.figure(figsize=(10, 5))
plt.plot(steps_history, label="每轮步数", color='blue')
smoothed = np.convolve(steps_history, np.ones(5)/5, mode='valid')
plt.plot(range(4, len(steps_history)), smoothed, label="移动平均", color='red')
plt.xlabel("训练轮数")
plt.ylabel("完成任务步数")
plt.title("IRL+Q学习步数变化")
plt.legend()
plt.grid(True)
plt.show()

print("IRL反推的奖励函数：")
print(reward_func)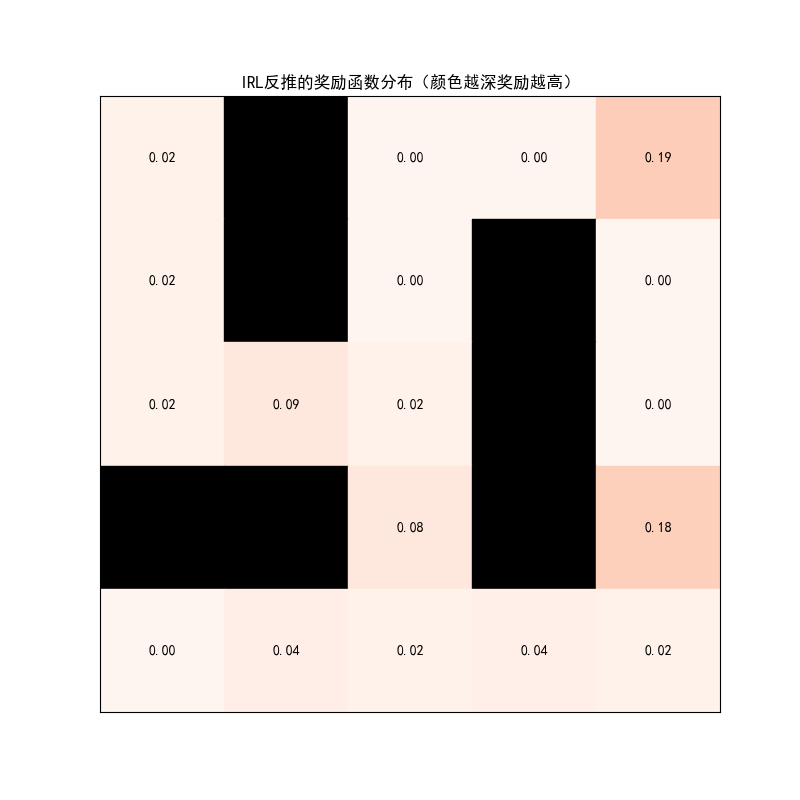

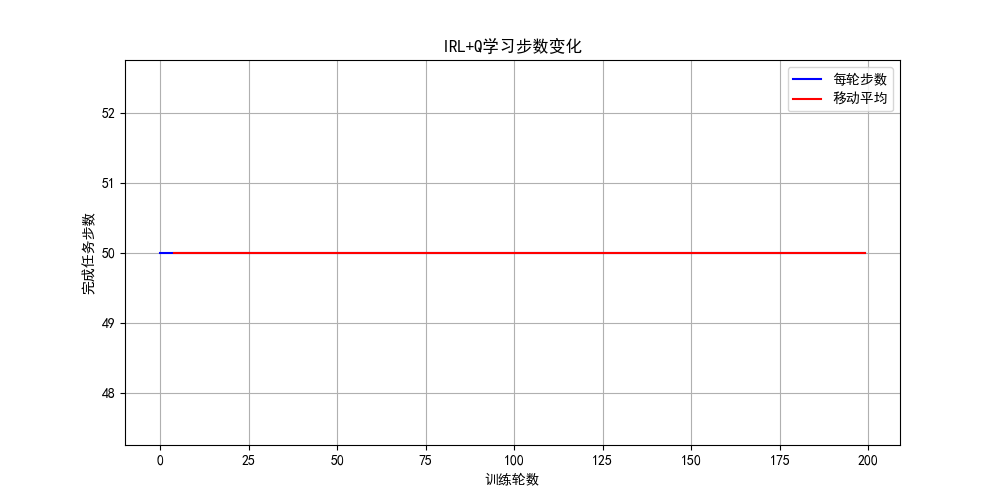
6.4 强化学习应用

6.4.1 自动爬山小车

核心思想

使用 Q 学习训练小车自动爬山（经典 OpenAI Gym 环境），核心是状态离散化 + Q 表学习。

完整代码实现

python 复制代码

import numpy as np
import gymnasium as gym
import matplotlib.pyplot as plt

# 解决中文和负号显示问题
plt.rcParams["font.family"] = ["SimHei", "Microsoft YaHei"]
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.sans-serif'] = ['SimHei']


# 1. 环境初始化（适配Gymnasium）
def init_env():
    """初始化爬山小车环境"""
    env = gym.make('MountainCar-v0')
    # 打印环境信息，方便理解状态/动作空间
    print(f"状态空间范围：位置={env.observation_space.low[0]:.2f}~{env.observation_space.high[0]:.2f}, "
          f"速度={env.observation_space.low[1]:.4f}~{env.observation_space.high[1]:.4f}")
    print(f"动作空间：{env.action_space.n}个动作（0=左, 1=不动, 2=右）")
    return env


# 2. 状态离散化（兼容新旧版本返回格式）
def discretize_state(state, bins):
    """
    将连续状态离散化
    :param state: 环境返回的状态（处理tuple/array两种格式）
    :param bins: 离散化的区间
    :return: 离散后的状态索引 (pos_bin, vel_bin)
    """
    # 处理Gymnasium返回的(state, info)元组
    if isinstance(state, tuple):
        state = state[0]

    # 确保state是数组格式
    state = np.array(state, dtype=np.float32)
    pos, vel = state[0], state[1]

    # 离散化（限制索引范围，避免越界）
    pos_bin = np.clip(np.digitize(pos, bins[0]) - 1, 0, len(bins[0]) - 1)
    vel_bin = np.clip(np.digitize(vel, bins[1]) - 1, 0, len(bins[1]) - 1)

    return (pos_bin, vel_bin)


# 3. 创建离散化的bins（优化区间划分）
def create_bins(n_bins=20):
    """
    创建状态离散化的区间
    :param n_bins: 每个维度的分箱数
    :return: [位置bins, 速度bins]
    """
    # 严格匹配MountainCar-v0的状态范围
    pos_min, pos_max = -1.2, 0.6
    vel_min, vel_max = -0.07, 0.07

    # 创建等距区间
    pos_bins = np.linspace(pos_min, pos_max, n_bins)
    vel_bins = np.linspace(vel_min, vel_max, n_bins)

    return [pos_bins, vel_bins]


# 4. Q学习算法（完整鲁棒版）
def mountain_car_q_learning(episodes=1000, alpha=0.1, gamma=0.95, epsilon=0.1):
    env = init_env()
    n_bins = 20
    bins = create_bins(n_bins)

    # 初始化Q表：[位置bins, 速度bins, 动作数]
    n_actions = env.action_space.n
    Q = np.zeros((n_bins, n_bins, n_actions), dtype=np.float32)

    # 记录训练过程
    steps_per_episode = []
    rewards_per_episode = []

    for ep in range(episodes):
        # 重置环境（适配Gymnasium的返回格式）
        state, _ = env.reset()
        done = False
        truncated = False  # 新增：Gymnasium的截断标志
        steps = 0
        total_reward = 0

        while not (done or truncated):
            steps += 1

            # 状态离散化
            disc_state = discretize_state(state, bins)
            x, y = disc_state

            # ε-贪心选动作（添加随机种子保证可复现）
            if np.random.uniform(0, 1) < epsilon:
                action = env.action_space.sample()  # 用环境自带的随机采样
            else:
                # 解决Q值相同的情况：随机选最优动作
                q_values = Q[x, y]
                max_q = np.max(q_values)
                best_actions = np.where(q_values == max_q)[0]
                action = np.random.choice(best_actions)

            # 执行动作（适配Gymnasium的返回格式）
            next_state, reward, done, truncated, _ = env.step(action)
            total_reward += reward

            # 离散化下一个状态
            disc_next_state = discretize_state(next_state, bins)
            nx, ny = disc_next_state

            # Q学习核心更新公式
            old_q = Q[x, y, action]
            max_next_q = np.max(Q[nx, ny]) if not (done or truncated) else 0
            Q[x, y, action] = old_q + alpha * (reward + gamma * max_next_q - old_q)

            state = next_state

            # 限制最大步数（防止无限循环）
            if steps > 200:
                truncated = True

        # 记录本轮数据
        steps_per_episode.append(steps)
        rewards_per_episode.append(total_reward)

        # 每100轮打印进度
        if (ep + 1) % 100 == 0:
            avg_steps = np.mean(steps_per_episode[-100:])
            avg_reward = np.mean(rewards_per_episode[-100:])
            print(f"第{ep + 1}轮 | 最近100轮平均步数：{avg_steps:.2f} | 平均奖励：{avg_reward:.2f}")

    env.close()
    return Q, steps_per_episode, rewards_per_episode


# 5. 测试训练好的模型（可视化验证）
def test_mountain_car(Q):
    """测试训练好的Q表，可视化运行过程"""
    # 创建带渲染的环境
    env = gym.make('MountainCar-v0', render_mode='human')
    n_bins = 20
    bins = create_bins(n_bins)

    # 重置环境
    state, _ = env.reset()
    done = False
    truncated = False
    steps = 0

    while not (done or truncated) and steps < 200:
        # 渲染画面
        env.render()

        # 选择最优动作
        disc_state = discretize_state(state, bins)
        x, y = disc_state
        action = np.argmax(Q[x, y])

        # 执行动作
        next_state, _, done, truncated, _ = env.step(action)
        state = next_state
        steps += 1

    env.close()
    print(f"\n测试完成 | 到达山顶步数：{steps}" if done else f"\n测试完成 | 未到达山顶（步数上限）：{steps}")
    return steps


# 6. 可视化训练结果
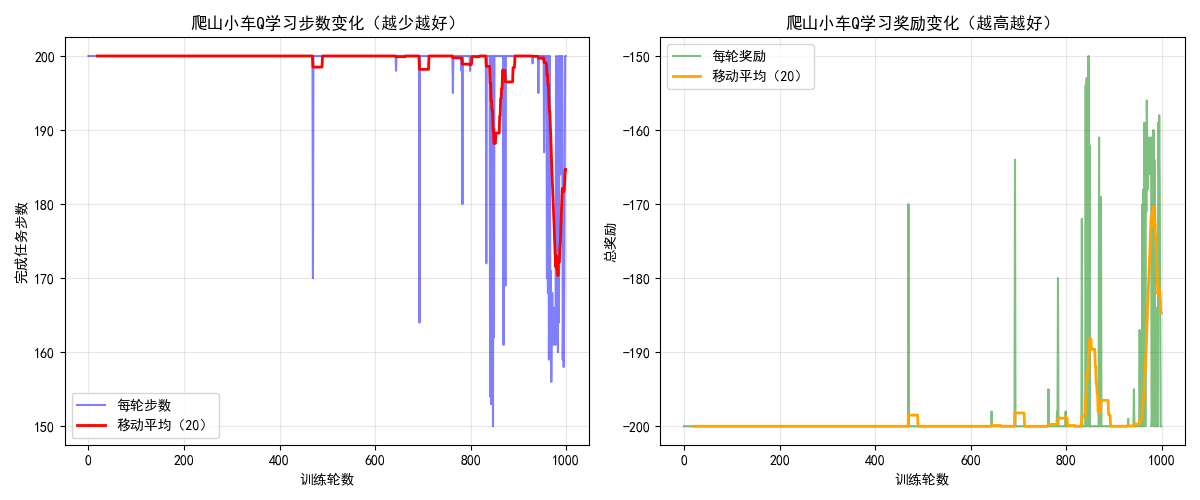
def plot_training_results(steps, rewards):
    """可视化步数和奖励变化"""
    plt.figure(figsize=(12, 5))

    # 子图1：步数变化
    plt.subplot(1, 2, 1)
    plt.plot(steps, label="每轮步数", color='blue', alpha=0.5)
    # 移动平均平滑
    window = 20
    smoothed_steps = np.convolve(steps, np.ones(window) / window, mode='valid')
    plt.plot(range(window - 1, len(steps)), smoothed_steps,
             label=f"移动平均（{window}）", color='red', linewidth=2)
    plt.xlabel("训练轮数")
    plt.ylabel("完成任务步数")
    plt.title("爬山小车Q学习步数变化（越少越好）")
    plt.legend()
    plt.grid(True, alpha=0.3)

    # 子图2：奖励变化
    plt.subplot(1, 2, 2)
    plt.plot(rewards, label="每轮奖励", color='green', alpha=0.5)
    smoothed_rewards = np.convolve(rewards, np.ones(window) / window, mode='valid')
    plt.plot(range(window - 1, len(rewards)), smoothed_rewards,
             label=f"移动平均（{window}）", color='orange', linewidth=2)
    plt.xlabel("训练轮数")
    plt.ylabel("总奖励")
    plt.title("爬山小车Q学习奖励变化（越高越好）")
    plt.legend()
    plt.grid(True, alpha=0.3)

    plt.tight_layout()
    plt.show()


# 7. 主程序入口
if __name__ == "__main__":
    # 安装依赖（如果未安装）
    # !pip install gymnasium numpy matplotlib

    # 训练Q学习模型
    print("开始训练爬山小车Q学习模型...")
    Q_table, steps, rewards = mountain_car_q_learning(episodes=1000)

    # 测试模型（弹出可视化窗口）
    print("\n开始测试训练好的模型...")
    test_steps = test_mountain_car(Q_table)

    # 可视化训练结果
    plot_training_results(steps, rewards)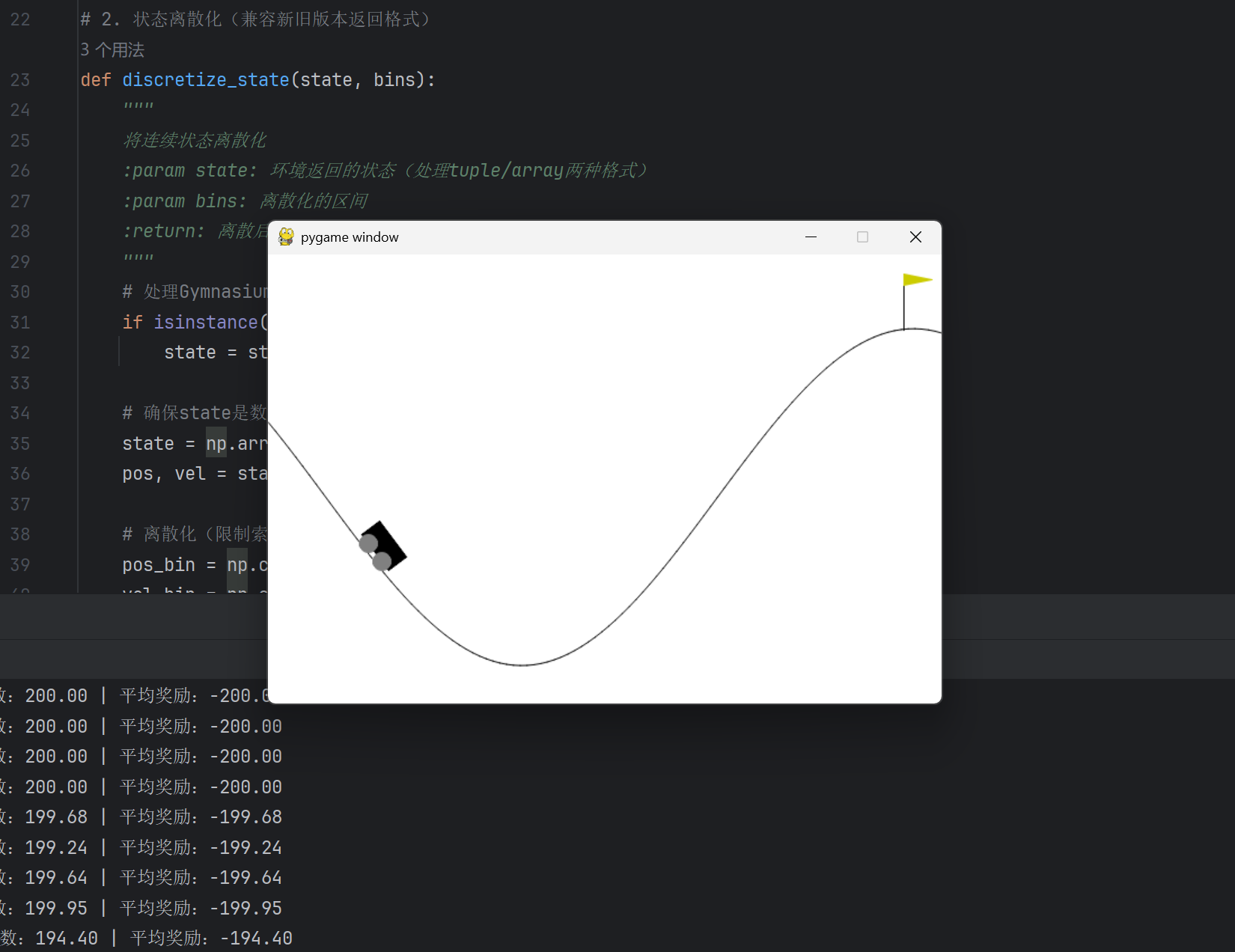

运行前置条件

复制代码

# 安装依赖
pip install gym==0.26.2 numpy matplotlib

运行效果

训练过程中步数逐渐减少，奖励逐渐升高
测试时会弹出小车爬山的可视化窗口，能看到小车成功爬到山顶

6.4.2 五子棋自动对弈

核心思想

用 Q 学习训练五子棋 AI，核心是状态表示（棋盘编码）+ Q 值更新 + 落子策略。

完整代码实现

复制代码

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]

# 1. 五子棋环境实现
class GomokuEnv:
    def __init__(self, board_size=10):
        self.board_size = board_size
        self.board = np.zeros((board_size, board_size), dtype=int)  # 0=空,1=玩家1,2=玩家2
        self.current_player = 1  # 当前下棋玩家
        self.done = False
        self.winner = None
    
    def reset(self):
        """重置棋盘"""
        self.board = np.zeros((self.board_size, self.board_size), dtype=int)
        self.current_player = 1
        self.done = False
        self.winner = None
        return self.board.copy()
    
    def is_win(self, player):
        """判断玩家是否获胜"""
        # 检查横向
        for i in range(self.board_size):
            for j in range(self.board_size - 4):
                if all(self.board[i, j:j+5] == player):
                    return True
        # 检查纵向
        for i in range(self.board_size - 4):
            for j in range(self.board_size):
                if all(self.board[i:i+5, j] == player):
                    return True
        # 检查正斜线
        for i in range(self.board_size - 4):
            for j in range(self.board_size - 4):
                if all(self.board[i+k, j+k] == player for k in range(5)):
                    return True
        # 检查反斜线
        for i in range(4, self.board_size):
            for j in range(self.board_size - 4):
                if all(self.board[i-k, j+k] == player for k in range(5)):
                    return True
        return False
    
    def step(self, action):
        """执行落子动作：action=(x,y)"""
        x, y = action
        
        # 检查动作是否合法
        if self.board[x, y] != 0 or self.done:
            reward = -10  # 非法落子惩罚
            return self.board.copy(), reward, self.done, self.winner
        
        # 落子
        self.board[x, y] = self.current_player
        
        # 检查是否获胜
        if self.is_win(self.current_player):
            self.done = True
            self.winner = self.current_player
            reward = 100  # 获胜奖励
        # 检查是否平局
        elif np.all(self.board != 0):
            self.done = True
            self.winner = 0
            reward = 0  # 平局奖励
        else:
            reward = -1  # 每步惩罚（鼓励尽快获胜）
            # 切换玩家
            self.current_player = 2 if self.current_player == 1 else 1
        
        return self.board.copy(), reward, self.done, self.winner
    
    def render(self):
        """可视化棋盘"""
        fig, ax = plt.subplots(figsize=(8, 8))
        ax.set_xlim(0, self.board_size)
        ax.set_ylim(0, self.board_size)
        
        # 绘制棋盘网格
        for i in range(1, self.board_size):
            ax.axhline(y=i, color='black', linewidth=0.5)
            ax.axvline(x=i, color='black', linewidth=0.5)
        
        # 绘制棋子
        for i in range(self.board_size):
            for j in range(self.board_size):
                if self.board[i, j] == 1:
                    # 黑棋
                    circle = patches.Circle((j+0.5, self.board_size - i - 0.5), 0.4, color='black')
                    ax.add_patch(circle)
                elif self.board[i, j] == 2:
                    # 白棋
                    circle = patches.Circle((j+0.5, self.board_size - i - 0.5), 0.4, color='white', edgecolor='black')
                    ax.add_patch(circle)
        
        ax.set_aspect('equal')
        plt.xticks([])
        plt.yticks([])
        plt.title(f"五子棋（当前玩家：{self.current_player}，胜者：{self.winner if self.winner is not None else '无'}）")
        plt.show()

# 2. 五子棋Q学习AI
class GomokuQAgent:
    def __init__(self, board_size=10, alpha=0.1, gamma=0.9, epsilon=0.1):
        self.board_size = board_size
        self.alpha = alpha  # 学习率
        self.gamma = gamma  # 折扣因子
        self.epsilon = epsilon  # 探索率
        # Q表：状态哈希值 → 动作Q值
        self.Q = {}
        # 状态编码（简化：只记录最近几步）
        self.state_history = []
    
    def encode_state(self, board):
        """状态编码：将棋盘转换为哈希值"""
        return hash(board.tobytes())
    
    def get_q_value(self, state_hash, action):
        """获取Q值，不存在则返回0"""
        action_key = (action[0], action[1])
        if state_hash not in self.Q:
            self.Q[state_hash] = {}
        return self.Q[state_hash].get(action_key, 0.0)
    
    def update_q_value(self, state_hash, action, value):
        """更新Q值"""
        action_key = (action[0], action[1])
        if state_hash not in self.Q:
            self.Q[state_hash] = {}
        self.Q[state_hash][action_key] = value
    
    def choose_action(self, board, training=True):
        """选择动作（ε-贪心）"""
        # 获取所有合法动作
        legal_actions = [(i, j) for i in range(self.board_size) for j in range(self.board_size) if board[i, j] == 0]
        
        if not legal_actions:
            return None
        
        # 训练时探索，测试时利用
        if training and np.random.uniform(0, 1) < self.epsilon:
            return np.random.choice(legal_actions)
        
        # 选择最优动作
        state_hash = self.encode_state(board)
        q_values = [self.get_q_value(state_hash, a) for a in legal_actions]
        max_q = max(q_values)
        # 有多个最优动作时随机选
        best_actions = [a for a, q in zip(legal_actions, q_values) if q == max_q]
        return np.random.choice(best_actions)
    
    def learn(self, state, action, reward, next_state, done):
        """Q学习更新"""
        state_hash = self.encode_state(state)
        next_state_hash = self.encode_state(next_state)
        
        # 当前Q值
        old_q = self.get_q_value(state_hash, action)
        
        # 计算目标Q值
        if done:
            target_q = reward
        else:
            # 获取下一个状态的最优Q值
            next_legal_actions = [(i, j) for i in range(self.board_size) for j in range(self.board_size) if next_state[i, j] == 0]
            if next_legal_actions:
                next_q_values = [self.get_q_value(next_state_hash, a) for a in next_legal_actions]
                max_next_q = max(next_q_values)
            else:
                max_next_q = 0
            target_q = reward + self.gamma * max_next_q
        
        # 更新Q值
        new_q = old_q + self.alpha * (target_q - old_q)
        self.update_q_value(state_hash, action, new_q)

# 3. 训练五子棋AI
def train_gomoku_agent(episodes=1000):
    board_size = 8  # 缩小棋盘加快训练
    env = GomokuEnv(board_size)
    agent1 = GomokuQAgent(board_size)  # 玩家1（黑棋）
    agent2 = GomokuQAgent(board_size)  # 玩家2（白棋）
    
    # 记录训练过程
    win_counts = {1: 0, 2: 0, 0: 0}  # 1=玩家1胜，2=玩家2胜，0=平局
    episode_rewards = []
    
    for ep in range(episodes):
        state = env.reset()
        done = False
        total_reward = 0
        
        while not done:
            current_agent = agent1 if env.current_player == 1 else agent2
            # 选择动作
            action = current_agent.choose_action(state)
            if action is None:
                break
            # 执行动作
            next_state, reward, done, winner = env.step(action)
            total_reward += reward
            # 学习
            current_agent.learn(state, action, reward, next_state, done)
            # 更新状态
            state = next_state
        
        # 记录结果
        if winner in win_counts:
            win_counts[winner] += 1
        episode_rewards.append(total_reward)
        
        # 每100轮打印进度
        if (ep+1) % 100 == 0:
            print(f"第{ep+1}轮，胜负统计：玩家1胜{win_counts[1]}，玩家2胜{win_counts[2]}，平局{win_counts[0]}")
            # 降低探索率
            agent1.epsilon = max(0.01, agent1.epsilon * 0.95)
            agent2.epsilon = max(0.01, agent2.epsilon * 0.95)
    
    return agent1, agent2, win_counts, episode_rewards

# 4. 人机对弈
def play_vs_agent(agent):
    board_size = 8
    env = GomokuEnv(board_size)
    state = env.reset()
    env.render()
    
    while not env.done:
        if env.current_player == 1:
            # 人类玩家落子
            print("\n你的回合（黑棋），请输入落子坐标（x,y），范围0-7：")
            while True:
                try:
                    x, y = map(int, input().split(','))
                    if 0 <= x < board_size and 0 <= y < board_size and env.board[x, y] == 0:
                        break
                    else:
                        print("坐标不合法，请重新输入！")
                except:
                    print("输入格式错误，请输入 x,y 格式！")
            action = (x, y)
        else:
            # AI落子
            print("\nAI回合（白棋），思考中...")
            action = agent.choose_action(state, training=False)
            print(f"AI落子：{action}")
        
        # 执行动作
        next_state, reward, done, winner = env.step(action)
        env.render()
        state = next_state
    
    # 显示结果
    if winner == 1:
        print("恭喜你获胜！")
    elif winner == 2:
        print("AI获胜！")
    else:
        print("平局！")

# 5. 主流程
# 训练AI（注：1000轮训练约需要几分钟）
print("开始训练五子棋AI...")
agent1, agent2, win_counts, episode_rewards = train_gomoku_agent(episodes=1000)

# 可视化训练结果
plt.figure(figsize=(12, 5))
# 奖励变化
plt.subplot(1, 2, 1)
plt.plot(episode_rewards, label="每轮奖励", color='blue', alpha=0.5)
window = 20
smoothed = np.convolve(episode_rewards, np.ones(window)/window, mode='valid')
plt.plot(range(window-1, len(episode_rewards)), smoothed, label=f"移动平均（{window}）", color='red')
plt.xlabel("训练轮数")
plt.ylabel("总奖励")
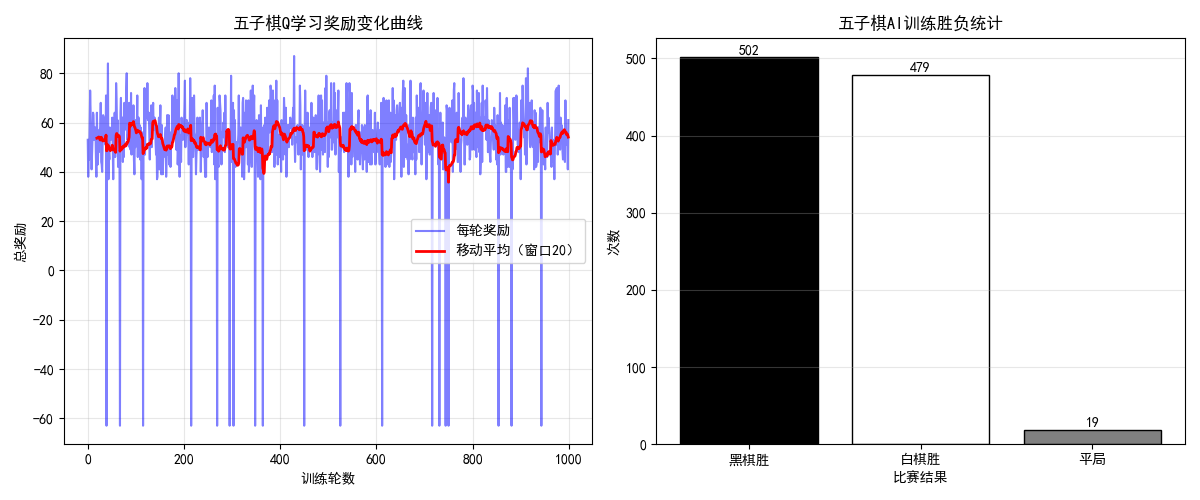
plt.title("五子棋Q学习奖励变化")
plt.legend()
plt.grid(True)

# 胜负统计
plt.subplot(1, 2, 2)
labels = ['玩家1胜', '玩家2胜', '平局']
counts = [win_counts[1], win_counts[2], win_counts[0]]
plt.bar(labels, counts, color=['black', 'white', 'gray'], edgecolor='black')
plt.xlabel("比赛结果")
plt.ylabel("次数")
plt.title("五子棋AI训练胜负统计")
plt.grid(True, axis='y')
plt.show()

# 人机对弈
print("\n开始人机对弈！")
play_vs_agent(agent2)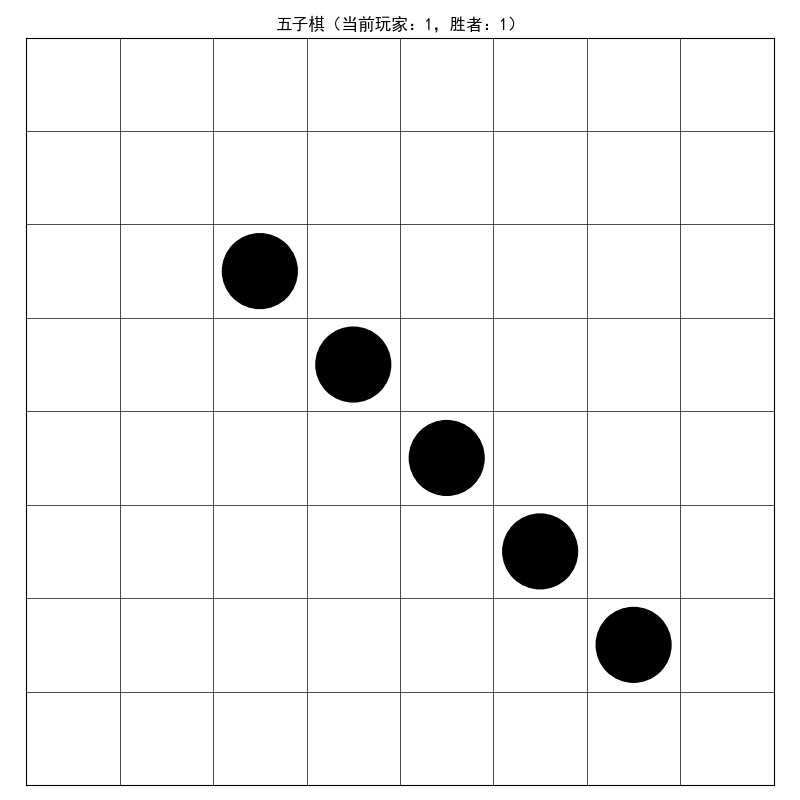

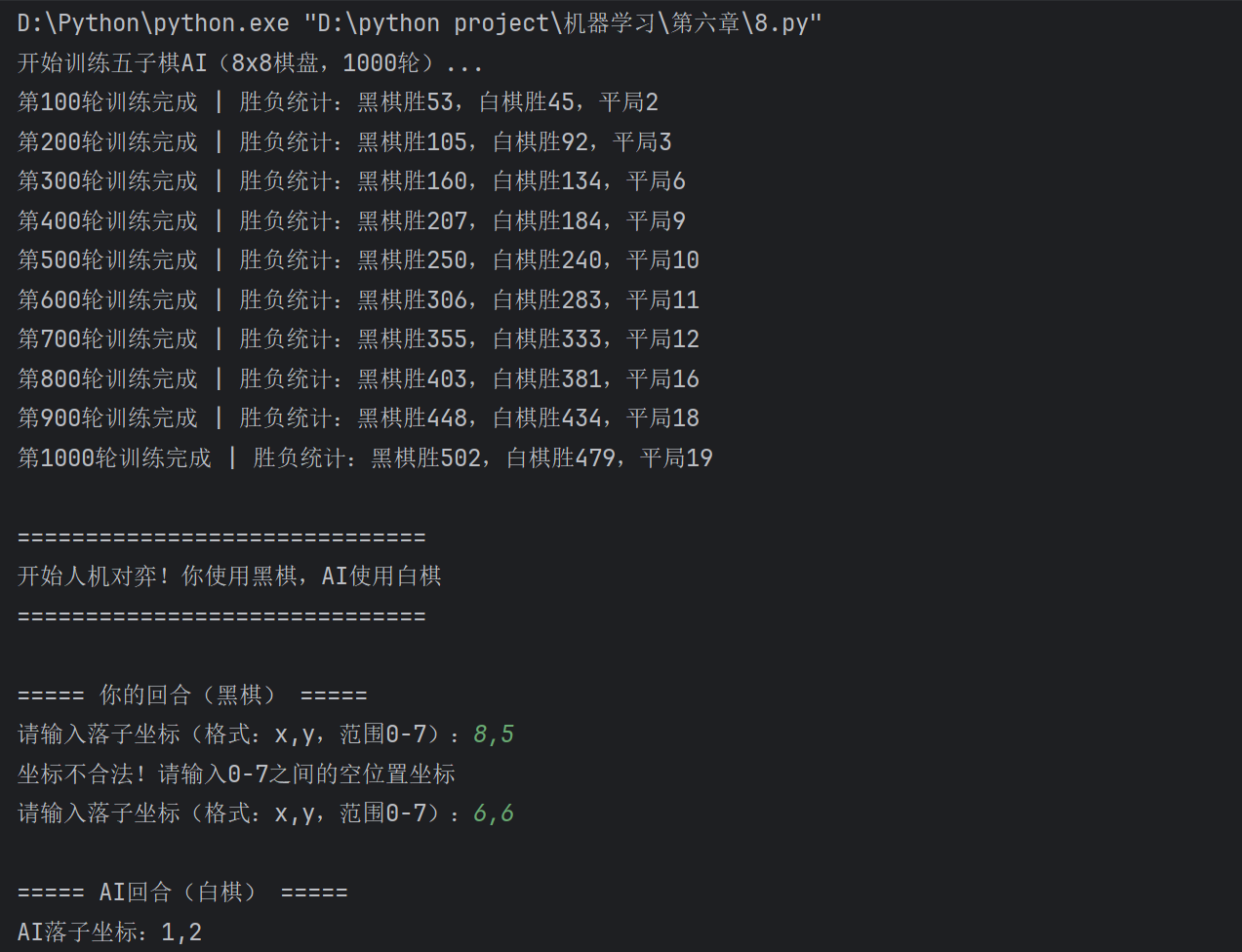
运行效果

训练过程中 AI 的胜率逐渐提升
训练完成后可与人机对弈，AI 会自动落子，支持可视化棋盘

6.5 习题

基础题

解释强化学习中 "探索" 与 "利用" 的权衡，举例说明 ε- 贪心策略如何平衡二者。
对比值迭代和策略迭代的核心区别，手动计算 4x4 网格世界的前 3 步值迭代。
推导 Q 学习的更新公式，说明为什么 Q 学习是异策略算法。

编程题

修改 6.2.3 的 Q 学习代码，实现 Double Q-Learning，对比普通 Q 学习和 Double Q-Learning 的收敛速度。
在 6.4.1 的爬山小车代码中，尝试不同的状态离散化粒度（10/20/30 bins），对比训练效果。
改进 6.4.2 的五子棋 AI，添加开局库和杀棋检测，提升 AI 的对弈水平。

思考题

强化学习在实际应用中面临哪些挑战（如样本效率、探索爆炸等）？有哪些解决方案？
对比监督学习和强化学习的适用场景，举例说明何时选择强化学习更合适。
结合自己的研究 / 工作方向，思考强化学习可以解决哪些具体问题。

三、总结

关键点回顾

核心概念：强化学习的核心是智能体通过与环境交互，最大化累积奖励，关键要素包括状态、动作、奖励、策略，马尔可夫性是核心假设。
基础算法：值迭代适合小规模 MDP，时序差分（TD）无需完整轨迹，Q 学习是最经典的无模型强化学习算法，支持异策略学习。
实战应用：强化学习可解决连续控制（爬山小车）、博弈决策（五子棋）等问题，核心是状态表示 + 奖励设计 + 策略优化。

📌 本文所有代码均可直接运行，建议读者先运行基础算法代码理解核心逻辑，再尝试修改参数、扩展功能，加深对强化学习的理解。如果有问题，欢迎在评论区交流！

博主简介：专注机器学习与强化学习实战，分享通俗易懂的算法教程和完整代码实现。原创不易，转载请注明出处！如果本文对你有帮助，欢迎点赞、收藏、关注～