硅基计划4.0 算法 动态规划进阶

文章目录

• 一、子序列系列（不连续子区间）
• • [1. 最长递增子序列](#1. 最长递增子序列)
  • [2. 摆动序列](#2. 摆动序列)
  • [3. 最长递增子序列个数](#3. 最长递增子序列个数)
  • [4. 最长数对链](#4. 最长数对链)
  • [5. 最长定差子序列](#5. 最长定差子序列)
  • [6. 最长斐波那契字序列长度](#6. 最长斐波那契字序列长度)
  • [7. 最长等差数列](#7. 最长等差数列)
  • [8. 等差数列划分II-子序列](#8. 等差数列划分II-子序列)
• 二、回文子串系列
• • [1. 回文字串个数](#1. 回文字串个数)
  • [2. 最长回文子串](#2. 最长回文子串)
  • [3. 回文串分割IV](#3. 回文串分割IV)
  • [4. 回文串分割II](#4. 回文串分割II)
  • [5. 最长回文子序列](#5. 最长回文子序列)
  • [6. 让字符串成为回文串的最少插入次数](#6. 让字符串成为回文串的最少插入次数)

---

一、子序列系列（不连续子区间）

1. 最长递增子序列

题目链接

注意我们求的是子序列，不是子数组，子序列的区间可以不连续，我们可以从左向右挑几个数，让挑的这几个数保持递增就好

因此我们可以这样定义状态表示，dp[i]表示以i位置为结尾的所有子系列中最长递增子序列的长度

因此，我们的状态转移方程可以这样推导

1. 如果是自己一个元素单独组成子序列，长度就是1
2. 如果和前面的子序列结合，那要保证前面的子序列也是递增，我们j下标从i开始依次向前枚举所有子序列，这样我们结合后
   
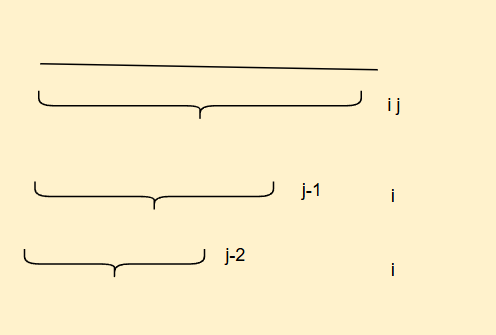
   只需要找到和前面哪个子序列结合后长度是最大的就好
   但是一般地，自己一个元素单独这种情况不用考虑，因为我们在初始化自动就处理了

综上所述，我们的状态转移方程就是dp[i] = Math.max(dp[i],dp[j-1]+1);

我们初始化，因为每个元素自己都可以组成子序列，因此dp表每个值都是1

并且我们从左往右填表，最后返回dp表的最大值就好

class Solution {
    public int lengthOfLIS(int[] nums) {
        int length = nums.length;
        //dp[i]表示以i位置为结尾的所有子序列中最长的严格递增的子序列
        int [] dp = new int[length];
        //因为默认一个元素也可以构成子序列，因此全部初始化为1
        Arrays.fill(dp,1);
        //跟踪最大值
        int ret = 1;
        //填表
        for(int i = 1;i < length;i++){
            for(int j = i-1;j >= 0;j--){
                if(nums[i] > nums[j]){
                    dp[i] = Math.max(dp[i],dp[j]+1);
                }
            }
            ret = Math.max(ret,dp[i]);
        }
        return ret;
    }
}

2. 摆动序列

题目链接

这一题非常类似于最长湍流子数组那一题，要保证一升一降，但是我们从子数组变成了子序列

我们定义状态表示，dp[i]表示以i位置为结尾的所有子序列中最长的摆动序列长度

我们想想我们做最长湍流子数组时候是不是定义了两个状态表示，因此我们这一题也要定义两个状态表示

dp1[i]表示以i位置为结尾的所有子序列中呈现上升趋势的最长摆动序列的长度，类似于↗️↘️↗️
dp2[i]表示以i位置为结尾的所有子序列中呈现下降趋势的最长摆动序列的长度，类似于↗️↘️↗️↘️

好，我们来推导下状态转移方程，过程和最长湍流子数组那道题非常类似

对于我们dp1来说

1. 如果只有i位置一个元素，长度就是1
2. 如果要和前面子序列结合，我们j下标从i-1开始往前走，寻找0~j的最长摆动序列长度，为了达到这种目的，我们要满足nums[i] > nums[j]，才能使得最后呈现↗️趋势，符合我们的状态表示，因此我们就要去寻找j和j-1呈现↘️趋势才可以，这不正好就是我们的dp2吗！

对于我我们dp2来说同理

1. 如果只有i位置一个元素，长度就是1
2. 如果要和前面子序列结合，要nums[i] < nums[j]并且j和j-1呈现↗️才可以，正好对应dp1

因此综上，我们的状态转移方程如下，同样在初始化已经考虑了自己一个元素单独作用情况

if(nums[i] > nums[j]){
	dp1[i] = Math.max(dp1[i],dp2[j]+1);
}
if(nums[i] < nums[j]){
	dp2[i] = Math.max(dp2[i],dp1[j]+1);
}

我们初始化和上一题一样，因为所有元素自己单独作用都可以构成子序列，因此都是1

我们按照从左向右填表，最后返回两个dp表的最大值

class Solution {
    public int wiggleMaxLength(int[] nums) {
        int length = nums.length;
        //dp1[i]表示以i位置为结尾的所有子序列中，在i下标元素和i-1下标元素之间呈现上升状态的，最长摆动序列的长度
        int [] dp1 = new int[length];
        //dp2[i]表示以i位置为结尾的所有子序列中，在i下标元素和i-1下标元素之间呈现下降状态的，最长摆动序列的长度
        int [] dp2 = new int[length];
        //初始化，题目说了自己一个数也可以构成子序列，因此默认值是1
        Arrays.fill(dp1,1);
        Arrays.fill(dp2,1);
        //跟踪最大值
        int ret1 = 1;
        int ret2 = 1;
        //填表
        for(int i = 1;i < length;i++){
            for(int j = i-1;j >= 0;j--){
                if(nums[i] > nums[j]){
                    dp1[i] = Math.max(dp1[i],dp2[j]+1);
                }
                if(nums[i] < nums[j]){
                    dp2[i] = Math.max(dp2[i],dp1[j]+1);
                }
            }
            ret1 = Math.max(dp1[i],ret1);
            ret2 = Math.max(dp2[i],ret2);
        }
        return Math.max(ret1,ret2);
    }
}

3. 最长递增子序列个数

题目链接

我们先来一个前置知识，如果我们想要找到数组中最大值出现的次数，比如nums = [1,1,2,4,5,6,6,9,9,9]，并且要求一次遍历就找到，我们可以这样

开始我们默认第一个是最大值，如果nums[i] < max，直接跳过看下一个

如果nums[i] == max，我们计数器就++

如果nums[i] > max，说明我们出现了一个更大的值，我们计数器清零，并且赋予新的最大值

好，我们根据这道题，定义状态表示，dp1[i]表示以i位置为结尾的最长递增子序列的长度，dp2[i]表示以i位置为结尾的最长递增子序列的个数

为什么要这么定义，看我们的状态转移方程推到过程就知道了

对于dp1的推导，我们第一题讲过了，这里直接拿过来dp1[i] = Math.max(dp1[i],dp2[j]+1)

对于dp2，且nums[j] < nums[i]（这样才能形成递增子序列）有三种情况

1. 若dp1[j]+1 = dp1[i]，说明我们找到了另一种能形成「以 i 结尾的最长子序列」的方式，这个长度正好符合i位置长度，说明这个长度的最长递增子序列出现了，因此我们dp2[i]就要加上dp2[j]。因为以j元素为结尾有很多种符合情况的递增子序列。比如以j结尾的最长递增子序列有5个，那么和i位置元素结合后，以i位置为结尾的最长递增子序列也是5个
2. 若dp1[j]+1 < dp1[i]，代表长度不足，要略过
3. 若dp1[j]+1 > dp1[i]，说明我们找到了更长的、以 i 结尾的子序列，超过了目前的最长长度，因此要重新统计最大长度，因此dp1[i] = dp1[j]+1，并且dp2[i] = dp2[j]

我们还是一样的全部初始化为1，并且从左向右填表，最后返回的时候利用我们最开始讲的策略

class Solution {
    public int findNumberOfLIS(int[] nums) {
        int length = nums.length;
        //lengths[i]表示以i位置为结尾的最长递增子序列的长度
        int [] lengths = new int[length];
        //count[i]表示以i位置为结尾的最长递增子序列的个数
        int [] count = new int[length];
        //初始化，全部为1
        Arrays.fill(lengths,1);
        Arrays.fill(count,1);
        //跟踪最终结果
        int max = 1;//目前最大长度
        int ret = 1;//目前的最大长度个数
        //填表
        for(int i = 1;i < length;i++){
            for(int j = i-1;j >= 0;j--){
                if(nums[i] > nums[j]){
                    if(lengths[j]+1 == lengths[i]){
                        count[i] += count[j];
                    }
                    if(lengths[j]+1 > lengths[i]){
                        //重新计数，说明长度更长
                        lengths[i] = lengths[j]+1;
                        count[i] = count[j];
                    }
                }
            }
            if(max == lengths[i]){
                ret += count[i];
            }
            if(max < lengths[i]){
                //更新最大值并重新计数
                max = lengths[i];
                ret = count[i];
            }
        }
        return ret;
    }
}

4. 最长数对链

题目链接

我们的数对链要求整体是上升的趋势，比如[[1,2],[2,3],[3,4]] --> [1,2],[3,4]

他们之间内部如果出现重复元素，是存在传递关系的

但是这一题我们发现，小的数对不一定在大的数对的左边（比如本应该是[1,2],[3,4]但是题目中可能是[3,4],[1,2]），整体不是有序的，不利于我们做动态规划，因此我们要排个序

我们这样定义状态表示，dp[i]表示以i位置为结尾的所有数对链中最长数对链长度

我们推导状态转移方程，如果我们是自己一个数对链，那么长度就是1

如果我们要和前面的数对链结合，并且p[j][1] < p[i][0]，即i位置数对链的第一个数大于j位置数对链的最后一个数，就可以说明i数对链和j数对链可以组合，因此就可以去找以j位置数对链为结尾的最长长度再+1

因此我们初始化全为1，因为自己一个数对链可以构成

并且我们从左向右填表，返回dp表的最大值

class Solution {
    public int findLongestChain(int[][] pairs) {
        int length = pairs.length;
        //dp[i]表示以i位置元素为结尾的所有数对链中长度最长的
        int [] dp = new int[length];
        //注意，原数组是乱序的，为了保证在动态规划比较元素过程中符合要求的数对始终在i位置之前
        //因此我们想根据整个数组进行升序排序
        Arrays.sort(pairs,(a,b)->a[0]-b[0]);
        //初始化，因为自己一个数对也可以形成数对链，因此初始化为1
        Arrays.fill(dp,1);
        //跟踪最大值
        int ret = 1;
        //填表
        for(int i = 1;i < length;i++){
            for(int j = i-1;j >= 0;j--){
                if(pairs[i][0] > pairs[j][1]){
                    dp[i] = Math.max(dp[i],dp[j]+1);
                }
            }
            ret = Math.max(ret,dp[i]);
        }
        return ret;
    }
}

5. 最长定差子序列

题目链接

根据题目，我们确定状态表示，dp[i]表示以i位置为结尾的所有子序列中最长的定差子序列长度

因为我们题目中是给了公差d的，因此我们可以推导出倒数第二个数字为nums[i]-d，往前一直找到符合nums[i]-d的值就好

如果nums[i]-d值不存在，那我们就nums[i]一个元素单独组成就好了

如果nums[i]-d值存在，且如果存在多个，并且是这样的关系

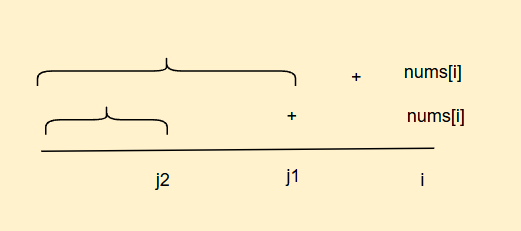
j1比j2更靠近i，说明j1组成的子序列长度更长，因为我们要的是最长的而不是个数，因此我们直接取j1的长度就好了

但是我们再想，我们每次j都要从i位置向前遍历寻找nums[i]-d的值，我们每次可能都要重复遍历，因此我们把nums[j]-d值和dp[j]的值绑定到哈希表中。并且我们可以直接在哈希表中做动态规划，进一步优化

我们要把第一个位置初始化为1，且hash[arr[0]] = 1（代表0号元素dp值为1）

并且从左往右填表，返回dp表最大值

class Solution {
    public int longestSubsequence(int[] arr, int difference) {
        //使用哈希表做动态规划
        //第一个元素表示以数组中某个值，第二个值表示最长定差子序列长度
        HashMap<Integer,Integer> hash = new HashMap<>();
        //跟踪结果
        int ret = 1;
        for(int tmp : arr){
            //寻找符合当前公差值，如果找不到就设置为0，然后加1表示tmp单独一个数形成子序列
            //否则我们就直接返回得到的哈希值再加上1
            hash.put(tmp,hash.getOrDefault(tmp-difference,0)+1);
            ret = Math.max(ret,hash.get(tmp));
        }
        return ret;
    }
}

6. 最长斐波那契字序列长度

题目链接

这一题我们根据经验，dp[i]表示以i位置元素为结尾的所有子序列中最长的斐波那契子序列长度

但是这样定义会导致我们只知道长度，并不知道其内部的具体数值

因为如果已知菲斐波那契数列的最后两个元素a,b，那么倒数第三个元素就是b-a，倒数第四个元素就是a-(b-a)

因此我们dp[i][j]表示以i和j位置元素为结尾的所有子序列中最长的斐波那契子序列长度

因此，我们来推导状态转移方程，分为三种情况

1. 如果a存在，并且在i位置元素之前，此时我们就要去找以k,i为结尾的最长递增子序列长度再+1，不就是dp[k][i]+1吗
2. 如果我们a存在，但是a下标在i,j之间，这就不符合要求，因为我们规定k,i,j是按顺序的，但是为了保证后续填表正确，我们dp值就是2。但是这里我我们可以优化下，我们不是要往前遍历去寻找a吗，然后找到下标，但是这样未必太慢了，我们可以这样，先把原数组中所有数字和下标绑定，这样当我们判断a存在后通过哈希表直接就可以获取下标

我们再来看初始化，因为我们长度最差的情况是2，因此都初始化为2

但是你会好奇，难道dp[0][0]不用考虑吗，其实不用，因为我们只会用到矩阵右上角的元素，即只会用到当i<j的时候元素

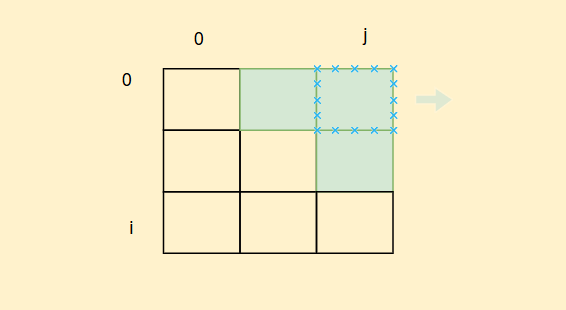
我们按照从上到下顺序填表，并且返回dp表最大值，但是如果数组本身只有三个元素并且还不是斐波那契数（比如1,2,4），这个时候我们ret默认是2

因此我们要特判，如果ret是2，我们就返回0

class Solution {
    public int lenLongestFibSubseq(int[] arr) {
        int length = arr.length;
        //dp[i][j]表示以i,j(i<j)两个位置元素为结尾的最长的斐波那契子数列长度
        int [][] dp = new int[length][length];
        //初始化，因为我们默认都是两个数，那么它的长度是2
        //不用担心dp[0][0]值影响判断，因为我们只会使用i<j情况的值
        for(int i = 0;i < length;i++){
            Arrays.fill(dp[i],2);
        }
        //为了更快的查找，我们提前把数组中每个元素以及它对应的下标存入哈希表中
        HashMap<Integer,Integer> hash = new HashMap<>();
        for(int i = 0;i < length;i++){
            hash.put(arr[i],i);
        }
        //跟踪最大长度
        int ret = 2;
        //填表
        for(int j = 2;j < length;j++){
            for(int i = j-1;i >= 0;i--){
                //查看数是否存在
                int num = arr[j]-arr[i];
                if(num < arr[i] && hash.containsKey(num)){
                    //存在就更新长度
                    dp[i][j] = dp[hash.get(num)][i]+1;
                }
                ret = Math.max(ret,dp[i][j]);
            }
        }
        //检查返回值，可能是这样的数组[1,2,7]此时ret存的是2，正确来说应该是0
        return ret <= 2 ? 0 : ret;
    }
}

7. 最长等差数列

题目链接

这一题我们根据经验，dp[i]表示以i位置元素为结尾的所有子序列中最长等差序列长度

但是问题就是我们只知道长度，并不知道公差，我们根本就不知道以i位置为结尾的子序列公差

因此根据我们上一题经验，我们dp[i][j]表示以i位置和j位置作为结尾（i<j）的所有子序列中最长的等差序列长度

因此如果我们知道最后两个元素，就可以退出倒数第三个元素

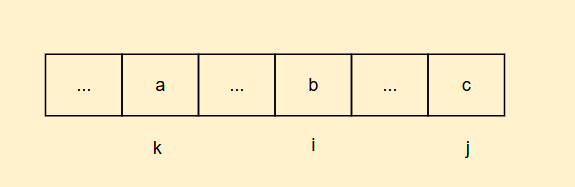
因此我们a = 2b-c

借此，我们分析状态转移方程

1. 如果我们要的a不存在，那我们单独b,c也可以构成等差序列，长度就是2
2. 如果我们要的a存在，但是下标在i,j之间，同样不合格要求，因此我们b,c单独构成等差序列，长度就是2
3. 如果我们要的a存在，并且在下标i,j之前，但是我们还要进一步讨论

和上一题一样，我们如果存在多种a取值，我们只需要靠近i位置的序列，因为这样长度可以最长，因此dp[i][j] = dp[k][i]+1

但是和上一题不一样的是，如果我们直接想前面找a这个数，整体时间复杂度会变成O(n³)

因此我们可以这样，我们使用哈希表，将所有的元素和其下标绑定（之前的题有这么做过），但是还要一个问题，就是如果数据量非常大，我们哈希表也要耗费时间查找，因此我们可以改进这个策略

就是我们在一边dp填表的时候，一边保存i位置前面元素以及下标，因为我们每次都是从i位置向前查找元素，不需要找i位置后面的元素

我们再来看初始化，我们默认的长度就是2，因为我们可以两个元素单独成一个子序列，还是和上一题一样，我们只会用到i<j位置元素，因此不用担心dp[0][0]初始化问题

这个填表顺序很有讲究，如果我们第一层循环固定序列的最后一个数，然后第二层循环枚举倒数第二个数，这样是不可以的，为什么？还记得我们的优化吗

我们的优化核心是保存i位置之前的元素，但是我们i一直是在变化的，就不能起到保存i位置前面的元素作用

因此，我们可以固定倒数第二个数（固定i），我们j再依次枚举最后一个数，这样我们j枚举完后，i向后走，顺便保存了i位置以前的元素以及它们的下标

这样我们到下一轮的时候，我们i位置以前的元素就已经被保存好了

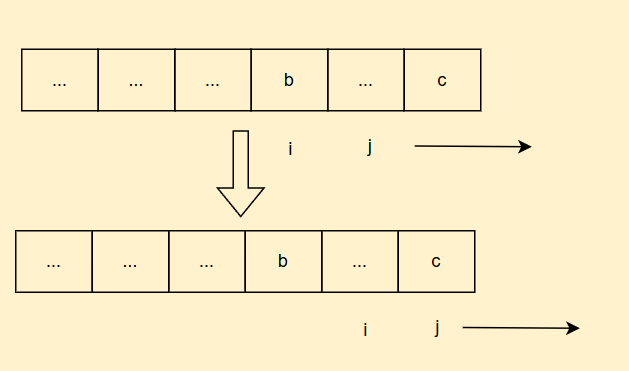
最后我们返回dp表的最大值就好

话说这一题真的是中等题吗（｀へ´）！

class Solution {
    public int longestArithSeqLength(int[] nums) {
        int length = nums.length;
        //dp[i][j]表示以i，j位置元素为结尾的最长等差数列长度
        int [][] dp = new int[length][length];
        //初始化，因为默认两个元素都可以构成子序列，因此初始化为2
        for(int i = 0;i < length;i++){
            Arrays.fill(dp[i],2);
        }
        //使用哈希表快速查找元素，分别绑定数组元素和下标
        HashMap<Integer,Integer> hash = new HashMap<>();
        //注意哈希表中我们要预先放置第一个元素值以及它的下标
        hash.put(nums[0],0);
        //开始填表，并跟踪最大值
        int ret = 2;
        for(int i = 1;i < length;i++){
            //注意我们先固定数列中倒数第二个元素，再去枚举倒数第一个元素
            //这样就可以让我们在填表完成后，顺便把距离i位置最近的数组元素以及下标放入哈希表
            for(int j = i+1;j < length;j++){
                //计算所需元素，设为x，满足x-nums[i] = nums[i]-nums[j]，移项变号得2*nums[i]-nums[j]
                int num = 2*nums[i]-nums[j];
                //查找是否存在
                if(hash.containsKey(num)){
                    //更新dp值
                    dp[i][j] = dp[hash.get(num)][i]+1;
                    //更新最大值
                    ret = Math.max(ret,dp[i][j]);
                }
            }
            //数组元素放入哈希表
            hash.put(nums[i],i);
        }
        return ret;
    }
}

8. 等差数列划分II-子序列

题目链接

这一题就是要我们求等叉子序列个数，我们等差数列至少要有三个元素，并且任意两个相邻元素公差相同

我们可以这样去定义状态表示，dp[i][j]表示以i,j位置元素为结尾的所有子序列中等差子序列的个数

我们由此来推断我们的状态转移方程，跟前两题一样，a可能有多个

但是这里我们求的不是最长长度，而是要把所有情况都统计下来

因此我们dp[i][j] += dp[k][i]（这里k可能有多种取值，我们都要统计）

但是还有一种情况我们漏了，就是单独k,i,j（这里k可能有多种取值，我们都要统计）三个元素构成情况，因此我们dpdp[i][j] += dp[k][i]+1

还是一样的，我们为了优化查找，使用哈希表让值和下标绑定，但是我们这个值可能有多个下标，因此我们可以使用HashMap<Integer,List<Integer>>统计

对于初始化方面，我们最坏的情况是只有两个元素结尾，但是两个元素是不能构成等差数列的，因此我们全部都是0

我们填表顺序还是和上一题一样，固定i位置元素，这样我们可以边填表边绑定

题目中求的是所有等差子序列，因此我们要返回dp表的所有值的和

class Solution {
    public int numberOfArithmeticSlices(int[] nums) {
        int length = nums.length;
        //dp[i][j]表示以i，j位置元素为结尾的所有等差子序列个数（i<j）
        int [][] dp = new int[length][length];
        //初始化，因为两个元素无法构成等差子序列，因此默认0就好
        //使用哈希表加快查询速度，不能使用HashSet存储下标因为在数据量大的时候，可能会调整位置
        HashMap<Long,List<Integer>> hash = new HashMap<>();
        //初始化元素值和下标
        for(int i = 0;i < length;i++){
            long num = (long)nums[i];
            if(!hash.containsKey(num)){
                hash.put(num,new ArrayList<>());
            }
            hash.get(num).add(i);
        }
        //跟踪个数
        int count = 0;
        //填表
        for(int j = 2;j < length;j++){
            //注意只用枚举到第二个数，因为序列至少为三个数
            for(int i = j-1;i >= 1;i--){
                //注意值可能会溢出
                long num = 2L*nums[i]-nums[j];
                //如果我想要找的值存在
                if(hash.containsKey(num)){
                    //遍历所有下标情况，加上
                    for(int index : hash.get(num)){
                        //如果有符合要求的值，就添加，如果碰到了不符合的马上跳出即可
                        //为什么这样能保证有序，因为我们都是从前向后添加下标的
                        //因此当第一次出现不符合要求的下标后，根据后续下标比当前下标还大的情况，直接提前终止就好
                        if(index < i){
                            dp[i][j] += dp[index][i]+1;
                            continue;
                        }
                        break;
                    }
                }
                count += dp[i][j];
            }
        }
        return count;
    }
}

二、回文子串系列

1. 回文字串个数

题目链接

这一题有很多解法，比如中心扩展算法和马拉车算法，但是这里我们只先介绍动态规划解法

并且注意，子串和子数组是一样的，是一个连续区间哦

这一题还说了，即使你的子串是长得一样的，但是只要里面的字符开始和结束位置不一样就好，比如

字符串aaa，里面三个a我分别用a1,a2,a3表示，那我们子串有
a1,a2,a3,a1a2,a1a3,a1a2a3共6个子串，你看即使有的子串长得一样，但是它们的内部位置不一样，就还是不一样的子串

既然这样，我们永二维dp表，用横坐标表示子串的起始位置，纵坐标表示子串的结束位置，并且我们还规定i=1 j=2和i=2,j=1是同种情况，因此我们只会使用到矩阵上三角部分，这也就说明了我们硬性条件i<=j

我们可以使用一个boolen类型dp表，用来表示这个区间是不是回文子串

我们接着来分析状态转移方程，如果str[i] != str[j]，说明根本无法构成回文串，直接false

如果str[i] == str[j]

1. 若i==j，说明是自己一个字符构成，当然可以构成，true
2. 若i+1 == j，说明它们两个相邻，也是回文串，因此true
3. 若i和j之间间隔着其他字符，我们要保证i+1和j-1这部分也要是回文子串，因此我们去dp[i+1][j-1]瞅瞅就好

对于初始化，其实我们可以不用特意初始化，因为我们只会用到上三角值，并且i==j也特判了

但是注意我们填表顺序，因为我们每次填表都要用到i+1,j-1，其中i是行，因此需要下一行状态，因此我们是从下往上填表

最后我们只需要看我们dp表有多少个true的状态就好

class Solution {
    public int countSubstrings(String s) {
        char [] ss = s.toCharArray();
        int length = ss.length;
        //dp[i][j]表示以i位置字符和j位置字符围成的子串中是否是回文子串
        boolean [][] dp = new boolean[length][length];
        //跟踪结果
        int ret = 0;
        //填表
        for(int i = length-1;i >= 0;i--){
            //枚举所有子串
            for(int j = i;j < length;j++){
                if(ss[i] == ss[j]){
                    //如果中间隔着其他字符，要看看中间字符情况，否则直接true
                    dp[i][j] = i-j < -1 ? dp[i+1][j-1] : true;
                }
                if(dp[i][j]){
                    ret++;
                }
            }
        }
        return ret;
    }
}

2. 最长回文子串

题目链接

这一题思路和上一题一样，我们只不过要用两个变量统计起始和结束位置下标，这样我们获取最长长度

class Solution {
    public String longestPalindrome(String s) {
        char [] ss = s.toCharArray();
        int length = ss.length;
        boolean [][] dp = new boolean[length][length];
        //统计最长子串起始下标和长度
        int begin = 0;
        int maxLength = 1;
        for(int i = length-1;i >= 0;i--){
            for(int j = i;j < length;j++){
                if(ss[i] == ss[j]){
                    dp[i][j] = i+1 < j ? dp[i+1][j-1] : true; 
                }
                if(dp[i][j] && j-i+1 > maxLength){
                    //长度变更
                    maxLength = j-i+1;
                    begin = i;
                }
            }
        }
        return s.substring(begin,begin+maxLength);
    }
}

3. 回文串分割IV

题目链接

这一题我们可以把字符串分割，然后三个子串都是回文的就好

还记得我们上一题写的回文串吗，我们是不是把所有子串的回文信息都统计了啊

这样，我们任取两个点i,j，把整个字符串分割为三个子串，分别是0~i-1，i~j，j+1~length-1三个子串区间，那我们直接看看三个子串是不是回文串就好啦

不就是我们上一题的dp[i][j]，因此我们直接判断

如果dp[0][i-1] && dp[i][j] && dp[i+1][lenth-1]都是回文子串，那么整个字符串就是回文的

并且判断回文后，我们可以直接跳出循环，仅仅需要判断一回就好了

class Solution {
    public boolean checkPartitioning(String s) {
        //这一题我们可以提前使用动态规划的dp表保存s中所有子串的回文信息
        char [] ss = s.toCharArray();
        int length = ss.length;
        boolean [][] dp = new boolean[length][length];
        for(int i = length-1;i >= 0;i--){
            for(int j = i;j < length;j++){
                if(ss[i] == ss[j]){
                    dp[i][j] = i+1 < j ? dp[i+1][j-1] : true;
                }
            }
        }
        //接着再次枚举所有子串，看能不能构成回文子串，能就返回true，否则直接就是false
        for(int i = 1;i < length;i++){
            for(int j = i;j < length-1;j++){
                if(dp[0][i-1] && dp[i][j] && dp[j+1][length-1]){
                    return true;
                }
            }
        }
        return false;
    }
}

4. 回文串分割II

题目链接

根据经验，dp[i]表示以i位置为结尾的最长子串（从0~i区间）分割为一个回文串所需要的最少分割次数

因此我们分析状态转移方程

1. 如果0~i区间就是回文串，我们不用切割了，dp[i] = 0
2. 如果0~i区间不是回文串，此时我们的j就是最后一个回文串的起始位置，此时我们要看看j~i区间是不是回文串

如果是回文串，则dp[j-1]+1，表示我们我们从j这里切一刀，此时0~j-1和j~i都是回文串了

如果不是回文串，说明这个切割方案就不是合理的

因此，我们dp[i] = Math.min(dp[j-1]+1,dp[i])

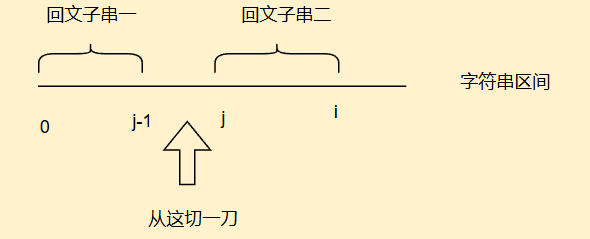
还有，我们拿到一个区间要判断这个区间是不是回文子串，因此我们可以先像第一题一样去处理下，统计所有子串的回文信息

对于初始化，为了不干扰我们判断，我们把dp表都初始化为+∞，这样我们求最小值的时候就不会误判0

最后我们返回dp表最后一个位置值就好

class Solution {
    public int minCut(String s) {
        //预处理字符串
        char [] ss = s.toCharArray();
        int length = ss.length;
        boolean [][] dp = new boolean[length][length];
        for(int i = length-1;i >= 0;i--){
            for(int j = i;j < length;j++){
                if(ss[i] == ss[j]){
                    dp[i][j] = i+1 < j ? dp[i+1][j-1] : true;
                }
            }
        }
        //正式分割回文串
        int [] dp1 = new int[length];
        //初始化
        Arrays.fill(dp1,Integer.MAX_VALUE);
        //填表
        for(int i = 0;i < length;i++){
            //判断0到i区间是不是回文串，如果是那就不用切割了
            if(dp[0][i]){
                dp1[i] = 0;
            }else{
                //进行切割
                for(int j = i;j >= 1;j--){
                    if(dp[j][i]){
                        //说明j到i是回文子串，要返回所有切割方案里的最小值
                        dp1[i] = Math.min(dp1[j-1]+1,dp1[i]);
                    }
                }
            }
        }
        return dp1[length-1];
    }
}

5. 最长回文子序列

题目链接

这一题思路就是我们第一题的思路

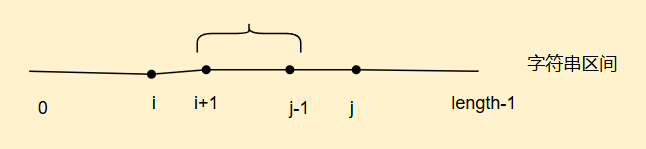
如果我们i+1和j-1区间的子串是一个回文串，且i位置字符和j位置字符相同，那我们本身就可以组成一个更长的回文字序列

因此我们dp[i][j]表示以字符串区间[i,j]区间内的所有子序列中最长回文子序列长度

因此我们来推导状态转移方程，如果str[i] == str[j]

1. 如果i==j，说明是一个字符，本身就是回文，长度为1
2. 如果i+1 == j，说明是相互错开，是回文序列，长度是2
3. 如果i和j隔着其他字符，则为dp[i+1][j-1]+2，也就是说在i和j区间内找到最长回文子序列，这不就是我们状态表示吗

如果str[i] != str[j]，此时这个回文字符就不能在i,j区间内，因此我们可以去更小的区间内寻找，就是在i+1~j和i,j-1区间内找

因此我们的状态转移方程就是dp[i][j] = Math.max(dp[i][j-1],dp[i+1][j])

但是i~j-1内部就包含了i+1~j-1情况·，并且i+1~j也包含了i+1~j-1情况，因此我们无需再特判i+1~j-1情况

对于初始化，因为我们状态转移方程可能会越界，但是我们dp[0][0]是在i==j情况才会发生，而这个情况我们已经进行特判过了，因此并不会越界

因为我们要的是下一行和当前行左边的值，因此我们要从下往上，从左到右填表

最后我们返回的是整个区间长度，因此就是dp[0][length-1]

class Solution {
    public int longestPalindromeSubseq(String s) {
        char [] ss = s.toCharArray();
        int length = ss.length;
        //dp[i][j]表示以i位置元素和j位置元素围成的子序列中的最长回文子序列长度（i<j）
        int [][] dp = new int[length][length];
        //填表
        for(int i = length-1;i >= 0;i--){
            for(int j = i;j < length;j++){
                if(ss[i] == ss[j]){
                    if(i == j){
                        //自己一个单独字符
                        dp[i][j] = 1;
                        continue;
                    }
                    if(i+1 == j){
                        //相邻字符
                        dp[i][j] = 2;
                        continue;
                    }
                    //中间包含其他字符
                    dp[i][j] = dp[i+1][j-1]+2;
                }else{
                    //此时i和j位置的值不能构成回文串，因此去更小的区间内看看
                    //去[i,j-1]和[i+1][j]区间内看看
                    dp[i][j] = Math.max(dp[i][j-1],dp[i+1][j]);
                }
            }
        }
        //返回整个区间内的最大值
        return dp[0][length-1];
    }
}

6. 让字符串成为回文串的最少插入次数

题目链接

这一题我们重用之前经验，dp[i][j]表示在i,j区间内的子串使它成为回文串的最小插入次数

因此我们来推导状态转移方程，如果str[i] == str[j]

1. 若i==j，一个字符就可以成为回文串，无需插入
2. 若i+1 == j，相互错开，也是回文串，无需插入
3. 若i和j之间隔着其他字符，此时因为str[i] == str[j]，两个端点就不用考虑了，因此我们只需要让i+1~j-1这段区间成为回文串就好，即dp[i+1][j-1]

如果str[i] != str[j]

想成为回文串，我们要保证两个端点的回文串相同

我们可以在i字符左边添加上str[j]，此时i-1位置字符就和j位置字符相同了，此时我们让i~j-1区间内成为回文串就好了

或者，我们可以在j字符右边添加上str[i]，此时i位置字符就和j+1位置字符相同了，此时我们让i+1~j成为回文串就好

我们要的是这两种情况最小值

对于初始化方面不用担心会越界，因为对于i==j情况我们已经特判过了

我们每次都要下一行和当前行左边的值，因此是从下往上填表，从左往右填表

最后我们要的是整个区间的状态，因此是dp[0][length-1]

class Solution {
    public int minInsertions(String s) {
        char [] ss = s.toCharArray();
        int length = ss.length;
        //dp[i][j]表示以i位置字符和j位置字符围成的区间内使其成为回文串的最小操作次数
        int [][] dp = new int[length][length];
        //填表
        for(int i = length-1;i >= 0;i--){
            //如果自己一个字符，本身就是回文串
            for(int j = i+1;j < length;j++){
                if(ss[i] == ss[j]){
                    //我们要让[i+1,j-1]内部成为一个回文串
                    dp[i][j] = dp[i+1][j-1];
                }else{
                    //此时我们可以在s[i+1]位置插入s[j]字符或者是s[j-1]位置插入s[i]字符
                    //此时分类讨论，我们要让[i+1,j]成为回文串或者是让[i-1,j]成为回文串
                    dp[i][j] = Math.min(dp[i+1][j],dp[i][j-1])+1;
                }
            }
        }
        return dp[0][length-1];
    }
}

---

感谢你的阅读

---

END