Codeforces Round 1072 (Div. 3)补题

没vp直接从后往前做的，只做出前四题

B 分类讨论 找规律

主要看最后一次反转后能流多长时间

• 若 s ≥ k s\geq k s≥k，最后反转后流s分钟
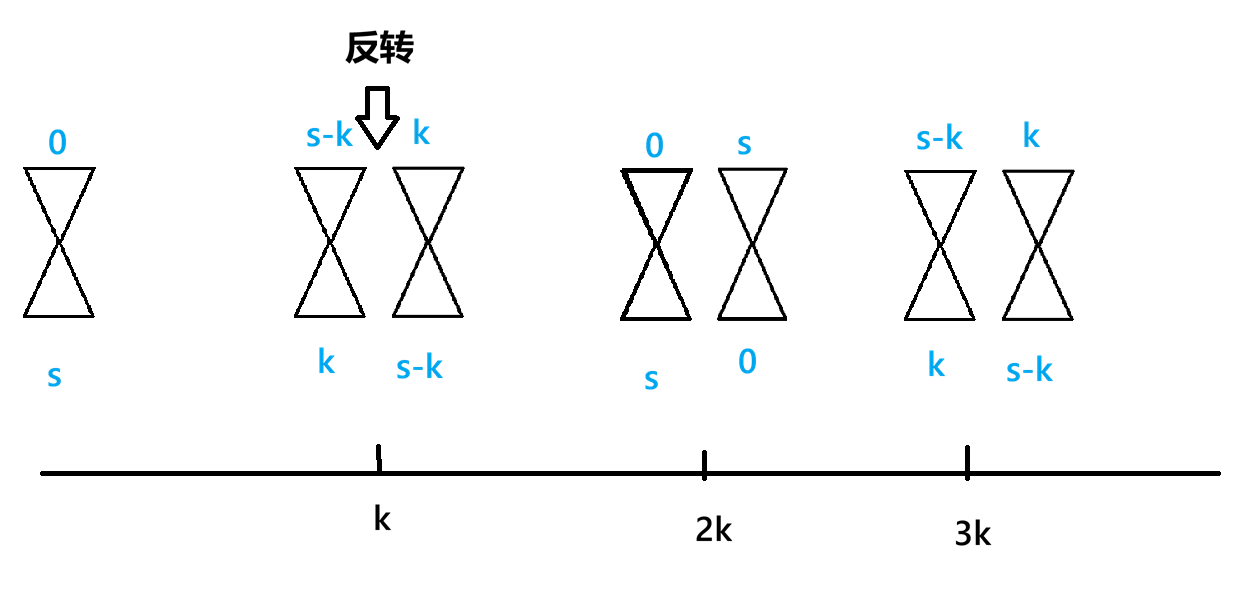
• s < k s< k s<k，如下图，翻转奇数次最后流k分钟，反转偶数次最后流s分钟

void solve(){
  int s,k,m;
  cin>>s>>k>>m;
  int tm=m/k,sm,ans;
  if(s<=k){
    sm=tm*k+s;
  }else{
    sm=tm*k+(tm%2?k:s);
  }
  ans=sm-m;
  cout<<max(ans,0ll)<<endl;
}

C 模拟 思维

2 30 ≥ 10 9 2^{30}\geq 10^9 230≥109暴力分解并遍历比较会超时

观察发现 x x x每次对半分，两堆的情况：x是偶数，都是 ⌊ x 2 ⌋ \lfloor{x\over 2}\rfloor ⌊2x⌋；x是奇数，两堆是 ⌊ x 2 ⌋ , ⌊ x 2 ⌋ + 1 \lfloor{x\over 2}\rfloor,\lfloor{x\over 2}\rfloor+1 ⌊2x⌋,⌊2x⌋+1一奇一偶

x是奇数再分解，一奇一偶中又会分解出奇数。所以出现过奇数后，分两堆一定是一奇一偶。

void solve(){
  int n,k;cin>>n>>k;
  int cnt1,cnt2,tm=0,fg=0;cnt1=cnt2=n;
  while(cnt1!=k&&cnt2!=k&&n>1){
    if(n&1)fg=1;//路径中出现过奇数 之后就会一直出现x,x+1的情况
    n>>=1;
    cnt1=cnt2=n;
    if(fg)cnt1++;
    tm++;
  }
  if(cnt1==k||cnt2==k)cout<<tm<<endl;
  else cout<<-1<<endl;
}

D 位运算 思维

思路来源

题意：对 1 ∼ n 1\sim n 1∼n每个数进行题设操作，计数步数超过k的数个数
÷ 2 , + 1 \div2,+1 ÷2,+1的操作很容易想到位运算

把一个二进制数通过题中操作变成0，需要把高位减半放到低位，低位-1去掉各数位上的1

e . g .111 , 最高位位置 x = 3 , 1 的个数 p = 3 , 需要的步数 s t e p = x − 1 + p = 5 e.g.111,最高位位置x=3,1的个数p=3,需要的步数step=x-1+p=5 e.g.111,最高位位置x=3,1的个数p=3,需要的步数step=x−1+p=5
a n s = k < s t e p 的个数 , s t e p ans=k<step的个数,step ans=k<step的个数,step有无限取值不好枚举，反向思考
c n t = k ≥ s t e p 的个数 , a n s = n − c n t cnt=k\geq step的个数,ans=n-cnt cnt=k≥step的个数,ans=n−cnt

枚举并分配 x x x和 p p p

注意题设 n = 2 d n=2^d n=2d，1的位置可以向低位任意分配而不会超过 n n n

int C[M][M];
void comb_init(){
  C[0][0]=C[1][1]=C[1][0]=1;
  forr(i,2,M){
    C[i][0]=C[i][i]=1;
    forr(j,1,i-1){
      C[i][j]=C[i-1][j]+C[i-1][j-1];
    }
  }
}
void solve(){
  int n,k;cin>>n>>k;
  int x=32-__builtin_clz(n),p=__builtin_popcount(n);
  //x:位数 p:重量 x+p<=k
  // cout<<x<<' '<<p<<endl;
  int cnt=0;
  if(x<=k)cnt++;
  forr(i,1,x-1){//一共i位二进制
    int mp=k-i+1;//maxp p的最大值
    //+1是因为只用移动消除低位即可 不用消除最高位
    if(mp<0)break;
    mp=min({mp,i});//i位上最多1的个数
    forr(tp,1,mp){//i位上1的个数
      cnt+=C[i-1][tp-1];//注意最高位必然是1 要-1
    }
  }
  cout<<n-cnt<<endl;
}