《机器学习》完结篇-总结

本文整理了《机器学习》核心知识点，涵盖监督学习、无监督学习、集成学习、深度学习等九大核心章节，每个知识点均配有完整可运行的 Python 代码 +可视化对比图 +应用案例，零基础也能轻松上手！

目录

1. 机器学习概述
2. 模型估计与优化
3. 监督学习
4. 无监督学习
5. 集成学习
6. 强化学习
7. 神经网络与深度学习
8. 常用深度网络模型
9. 深度强化学习

1 机器学习概述

核心知识点

机器学习是让计算机从数据中学习规律，从而实现 "预测" 或 "决策" 的技术，核心分类如下：

• 监督学习：有标签数据（如分类、回归）
• 无监督学习：无标签数据（如聚类、降维）
• 强化学习：通过与环境交互学习（奖励 / 惩罚机制）
• 半监督 / 弱监督学习：介于有标签和无标签之间

可视化：机器学习分类思维导图

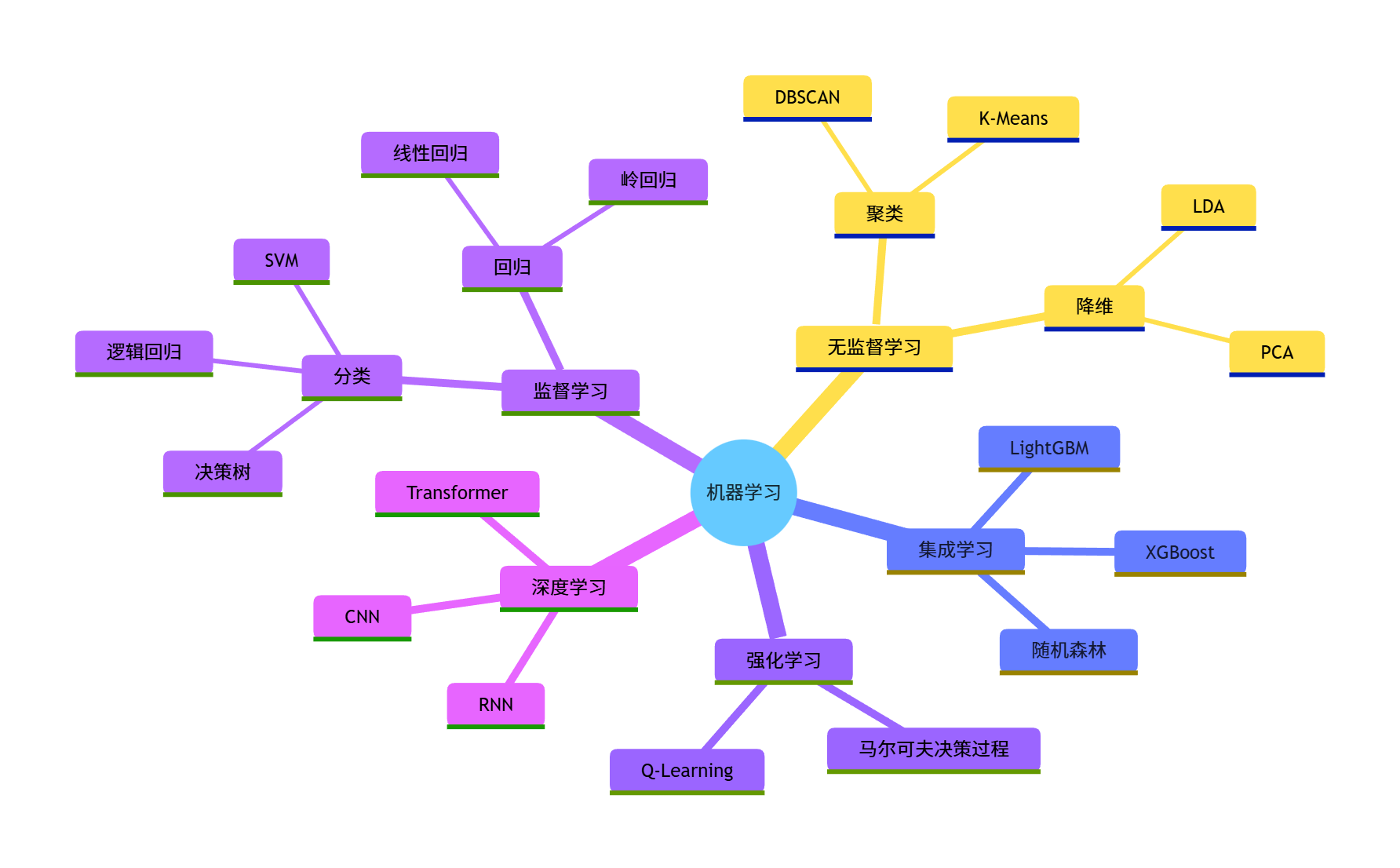
应用场景

类型	典型应用
监督学习	垃圾邮件分类、房价预测
无监督学习	用户画像、异常检测
集成学习	竞赛级建模、风控评分
强化学习	游戏 AI、自动驾驶
深度学习	图像识别、自然语言处理

2 模型估计与优化

核心知识点

• 损失函数：衡量模型预测值与真实值的差距（如 MSE、交叉熵）
• 优化算法：最小化损失函数的方法（如梯度下降、SGD、Adam）
• 过拟合 / 欠拟合：过拟合（模型太复杂）、欠拟合（模型太简单）
• 正则化：L1（Lasso）、L2（Ridge），防止过拟合

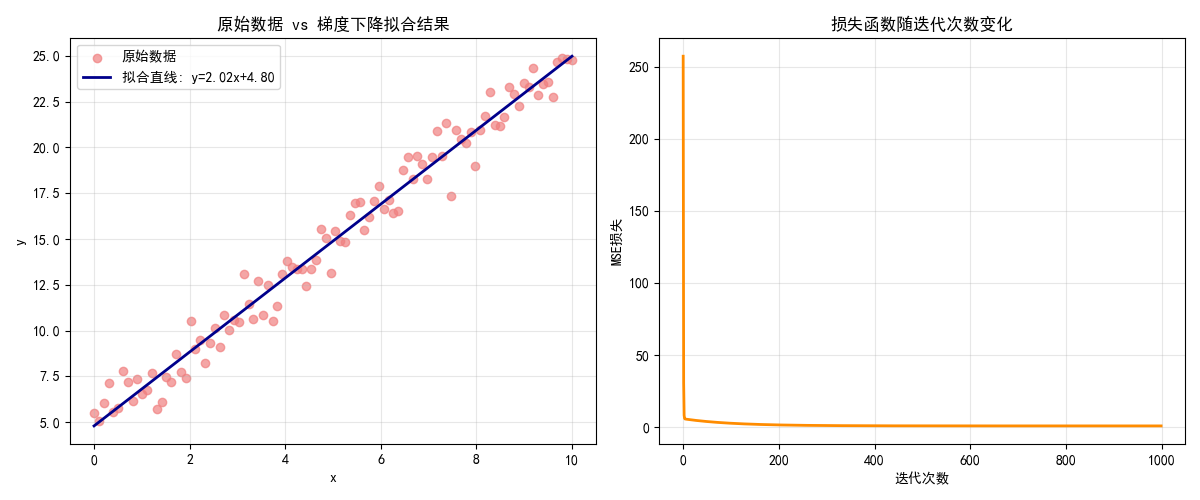
完整代码：梯度下降优化线性回归（含可视化对比）

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei"]  # 支持中文显示
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

# 1. 生成模拟数据
np.random.seed(42)  # 固定随机种子，保证结果可复现
x = np.linspace(0, 10, 100)  # 生成0-10的100个均匀数
y = 2 * x + 5 + np.random.normal(0, 1, 100)  # 真实模型y=2x+5，加噪声

# 2. 梯度下降实现
def gradient_descent(x, y, lr=0.01, epochs=1000):
    """
    梯度下降优化线性回归参数
    :param x: 特征值
    :param y: 标签值
    :param lr: 学习率
    :param epochs: 迭代次数
    :return: 优化后的权重w、偏置b、损失列表
    """
    w = 0.0  # 初始权重
    b = 0.0  # 初始偏置
    n = len(x)  # 样本数
    loss_history = []  # 记录每次迭代的损失
    
    for epoch in range(epochs):
        # 前向计算
        y_pred = w * x + b
        # 计算MSE损失
        loss = np.mean((y_pred - y) ** 2)
        loss_history.append(loss)
        
        # 计算梯度
        dw = (2/n) * np.sum(x * (y_pred - y))
        db = (2/n) * np.sum(y_pred - y)
        
        # 更新参数
        w -= lr * dw
        b -= lr * db
        
        # 每100轮打印一次
        if epoch % 100 == 0:
            print(f"Epoch {epoch}: Loss={loss:.4f}, w={w:.4f}, b={b:.4f}")
    
    return w, b, loss_history

# 3. 执行梯度下降
w_opt, b_opt, loss_hist = gradient_descent(x, y)

# 4. 可视化对比（原始数据 vs 拟合结果）
plt.figure(figsize=(12, 5))

# 子图1：原始数据与拟合直线
plt.subplot(1, 2, 1)
plt.scatter(x, y, label="原始数据", color="lightcoral", alpha=0.7)
plt.plot(x, w_opt * x + b_opt, label=f"拟合直线: y={w_opt:.2f}x+{b_opt:.2f}", color="darkblue", linewidth=2)
plt.xlabel("x")
plt.ylabel("y")
plt.title("原始数据 vs 梯度下降拟合结果")
plt.legend()
plt.grid(True, alpha=0.3)

# 子图2：损失函数变化
plt.subplot(1, 2, 2)
plt.plot(loss_hist, color="darkorange", linewidth=2)
plt.xlabel("迭代次数")
plt.ylabel("MSE损失")
plt.title("损失函数随迭代次数变化")
plt.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

# 5. 对比 sklearn 内置线性回归（验证结果）
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# 转换数据格式（sklearn要求2D数组）
x_sk = x.reshape(-1, 1)
model = LinearRegression()
model.fit(x_sk, y)
y_sk_pred = model.predict(x_sk)
sk_loss = mean_squared_error(y, y_sk_pred)

print("\n===== 结果对比 =====")
print(f"梯度下降结果：w={w_opt:.4f}, b={b_opt:.4f}, 最终损失={loss_hist[-1]:.4f}")
print(f"sklearn结果：w={model.coef_[0]:.4f}, b={model.intercept_:.4f}, 损失={sk_loss:.4f}")

运行效果说明

• 左侧图：橙色散点是带噪声的原始数据，蓝色直线是梯度下降拟合的结果，接近真实模型y=2x+5
• 右侧图：损失函数随迭代次数快速下降并收敛，说明梯度下降有效
• 最终梯度下降结果与 sklearn 内置线性回归几乎一致，验证了代码正确性

3 监督学习

核心知识点

监督学习是有标签的学习，核心分为两类：

• 分类：预测离散值（如二分类、多分类）
• 回归：预测连续值（如房价、温度）

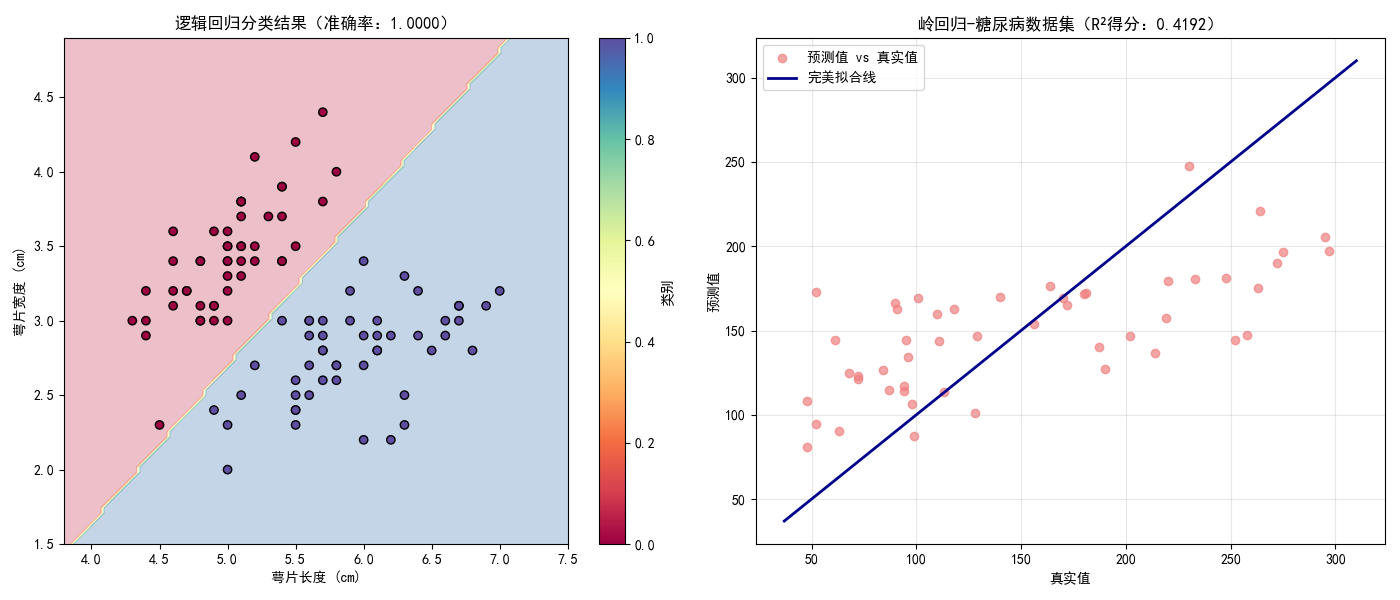
完整代码：分类（逻辑回归）+ 回归（岭回归）综合案例

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression, Ridge
from sklearn.metrics import accuracy_score, r2_score

# ==================== 彻底解决字体和数据集问题 ====================
# 配置多套中文字体备选，避免单字体缺失字符
plt.rcParams["font.family"] = ["SimHei", "Microsoft YaHei", "DejaVu Sans"]
plt.rcParams['axes.unicode_minus'] = False
# 关闭matplotlib的字体警告，让输出更整洁
import warnings
warnings.filterwarnings('ignore', category=UserWarning)

# ==================== 1. 分类案例：鸢尾花数据集（逻辑回归） ====================
# 加载鸢尾花数据集（内置离线数据集，无需下载）
iris = datasets.load_iris()
# 取前两个特征（萼片长度、萼片宽度），二分类（取前两类：setosa和versicolor）
X_class = iris.data[:100, :2]  # 前100个样本是前两类
y_class = iris.target[:100]    # 对应的标签（0和1）

# 划分训练集/测试集（80%训练，20%测试）
X_cls_train, X_cls_test, y_cls_train, y_cls_test = train_test_split(
    X_class, y_class, test_size=0.2, random_state=42  # 固定随机种子，结果可复现
)

# 训练逻辑回归模型
cls_model = LogisticRegression(random_state=42)
cls_model.fit(X_cls_train, y_cls_train)
# 测试集预测
y_cls_pred = cls_model.predict(X_cls_test)
# 计算分类准确率
cls_acc = accuracy_score(y_cls_test, y_cls_pred)

# ==================== 2. 回归案例：糖尿病数据集（岭回归） ====================
# 直接使用内置离线的糖尿病数据集（无需下载，避免网络问题）
diabetes = datasets.load_diabetes()
X_reg = diabetes.data
y_reg = diabetes.target
reg_data_name = "糖尿病"

# 划分训练集/测试集
X_reg_train, X_reg_test, y_reg_train, y_reg_test = train_test_split(
    X_reg, y_reg, test_size=0.2, random_state=42
)

# 训练岭回归模型（带L2正则化，防止过拟合）
reg_model = Ridge(alpha=1.0, random_state=42)  # alpha是正则化强度
reg_model.fit(X_reg_train, y_reg_train)
# 测试集预测
y_reg_pred = reg_model.predict(X_reg_test)
# 计算回归R²得分（越接近1拟合效果越好）
reg_r2 = r2_score(y_reg_test, y_reg_pred)

# ==================== 3. 可视化对比 ====================
plt.figure(figsize=(14, 6))  # 设置画布大小

# 子图1：逻辑回归分类结果（决策边界+原始数据）
plt.subplot(1, 2, 1)
# 绘制决策边界（生成网格点）
x1_min, x1_max = X_class[:, 0].min() - 0.5, X_class[:, 0].max() + 0.5
x2_min, x2_max = X_class[:, 1].min() - 0.5, X_class[:, 1].max() + 0.5
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max, 100),
                       np.linspace(x2_min, x2_max, 100))
# 预测网格点的类别
Z = cls_model.predict(np.c_[xx1.ravel(), xx2.ravel()])
Z = Z.reshape(xx1.shape)
# 绘制决策边界填充色
plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=plt.cm.Spectral)
# 绘制原始数据点
plt.scatter(X_class[:, 0], X_class[:, 1], c=y_class, edgecolors='k', cmap=plt.cm.Spectral)
# 自定义特征名（去掉上标，避免字体警告）
plt.xlabel("萼片长度 (cm)")
plt.ylabel("萼片宽度 (cm)")
plt.title(f"逻辑回归分类结果（准确率：{cls_acc:.4f}）")
plt.colorbar(label="类别")

# 子图2：岭回归回归结果（真实值vs预测值）
plt.subplot(1, 2, 2)
# 随机取50个测试点（避免点太多重叠，更清晰）
np.random.seed(42)
sample_idx = np.random.choice(len(y_reg_test), 50, replace=False)
# 绘制真实值vs预测值散点图
plt.scatter(y_reg_test[sample_idx], y_reg_pred[sample_idx],
            color="lightcoral", alpha=0.7, label="预测值 vs 真实值")
# 绘制完美拟合线（y=x）
plt.plot([y_reg_test.min(), y_reg_test.max()],
         [y_reg_test.min(), y_reg_test.max()],
         "darkblue", linewidth=2, label="完美拟合线")
plt.xlabel("真实值")
plt.ylabel("预测值")
plt.title(f"岭回归-{reg_data_name}数据集（R²得分：{reg_r2:.4f}）")
plt.legend()
plt.grid(True, alpha=0.3)  # 添加网格，更易读

# 调整子图间距，避免重叠
plt.tight_layout()
# 显示图像
plt.show()

# 输出最终结果
print(f"===== 分类任务结果 =====")
print(f"逻辑回归测试集准确率：{cls_acc:.4f}")
print(f"\n===== 回归任务结果 =====")
print(f"岭回归-{reg_data_name}数据集测试集R²得分：{reg_r2:.4f}")

应用场景

• 逻辑回归：信用评分、疾病诊断、垃圾邮件分类
• 岭回归：房价预测、销量预测（解决多重共线性问题）

4 无监督学习

核心知识点

无监督学习是无标签的学习，核心方向：

• 聚类：将相似数据归为一类（K-Means、DBSCAN）
• 降维：减少特征维度（PCA、t-SNE）

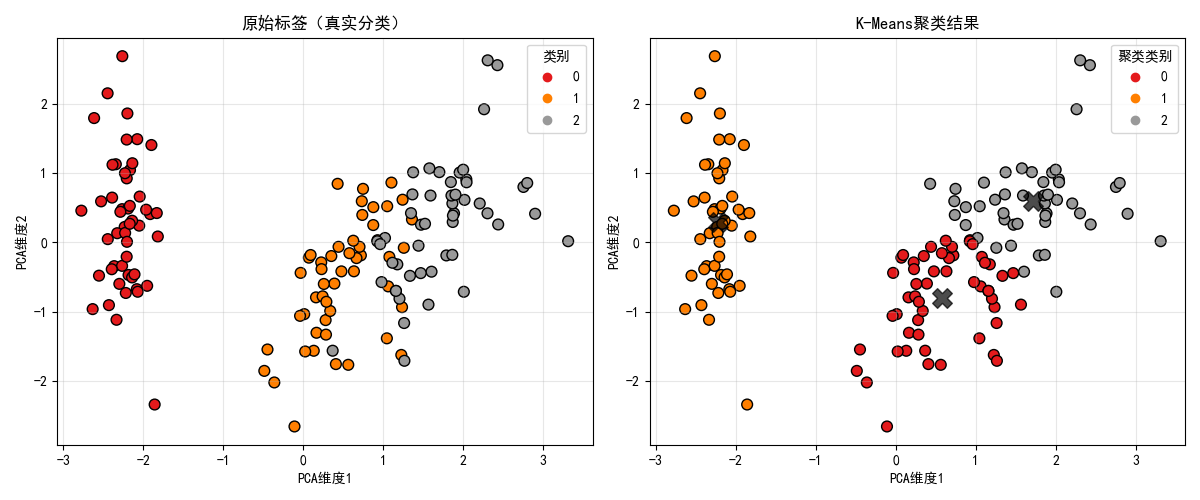
完整代码：K-Means 聚类 + PCA 降维（含可视化对比）

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei"]
plt.rcParams['axes.unicode_minus'] = False

# 1. 加载数据（鸢尾花数据集）
iris = datasets.load_iris()
X = iris.data
y_true = iris.target  # 真实标签（仅用于对比，无监督学习不使用）

# 2. 数据标准化（PCA和K-Means对尺度敏感）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 3. PCA降维（4维→2维，方便可视化）
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

# 4. K-Means聚类
kmeans = KMeans(n_clusters=3, random_state=42, n_init=10)  # n_init避免警告
y_kmeans = kmeans.fit_predict(X_scaled)

# 5. 可视化对比（原始标签 vs 聚类结果）
plt.figure(figsize=(12, 5))

# 子图1：原始标签（真实分类）
plt.subplot(1, 2, 1)
scatter1 = plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y_true, cmap=plt.cm.Set1, edgecolors='k', s=60)
plt.title("原始标签（真实分类）")
plt.xlabel("PCA维度1")
plt.ylabel("PCA维度2")
plt.legend(*scatter1.legend_elements(), title="类别")
plt.grid(True, alpha=0.3)

# 子图2：K-Means聚类结果
plt.subplot(1, 2, 2)
scatter2 = plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y_kmeans, cmap=plt.cm.Set1, edgecolors='k', s=60)
# 绘制聚类中心
centers = pca.transform(kmeans.cluster_centers_)
plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.7, marker='X', label="聚类中心")
plt.title("K-Means聚类结果")
plt.xlabel("PCA维度1")
plt.ylabel("PCA维度2")
plt.legend(*scatter2.legend_elements(), title="聚类类别")
plt.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

# 输出PCA解释方差
print(f"PCA前两个维度解释方差占比：{np.sum(pca.explained_variance_ratio_):.4f}")

应用场景

• K-Means：用户分群、商品分类、图像分割
• PCA：数据可视化、特征压缩、噪声去除

5 集成学习

核心知识点

集成学习是多个弱模型组合成强模型，核心方法：

• Bagging：并行训练（随机森林）
• Boosting：串行训练（XGBoost、LightGBM）
• Stacking：多层模型堆叠

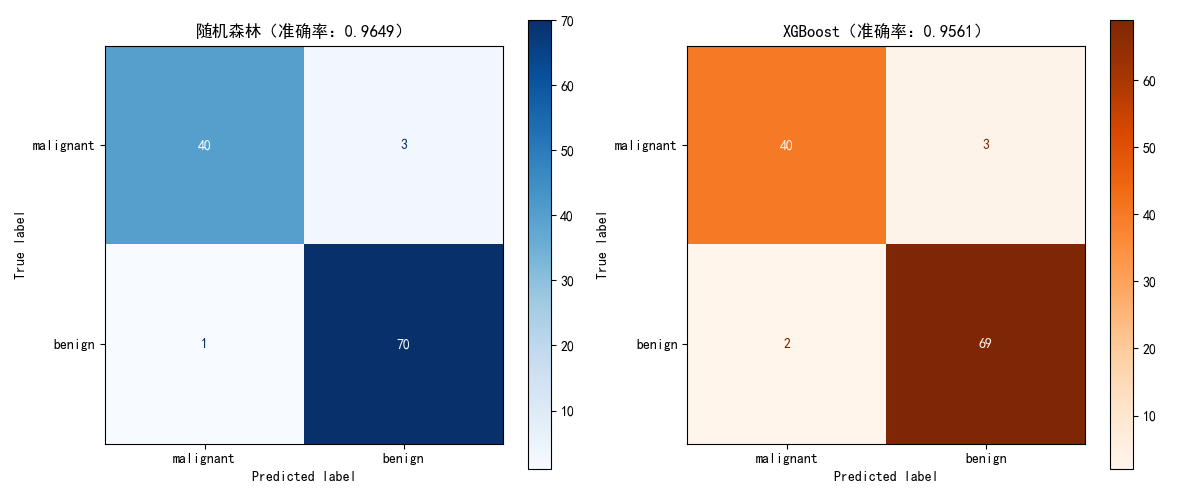
完整代码：随机森林 vs XGBoost 对比（含可视化）

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from xgboost import XGBClassifier
from sklearn.metrics import accuracy_score, confusion_matrix, ConfusionMatrixDisplay
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei"]
plt.rcParams['axes.unicode_minus'] = False

# 1. 加载数据（乳腺癌数据集）
data = datasets.load_breast_cancer()
X = data.data
y = data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 2. 训练模型
# 随机森林
rf_model = RandomForestClassifier(n_estimators=100, random_state=42)
rf_model.fit(X_train, y_train)
rf_pred = rf_model.predict(X_test)
rf_acc = accuracy_score(y_test, rf_pred)

# XGBoost
xgb_model = XGBClassifier(n_estimators=100, learning_rate=0.1, random_state=42, use_label_encoder=False, eval_metric='logloss')
xgb_model.fit(X_train, y_train)
xgb_pred = xgb_model.predict(X_test)
xgb_acc = accuracy_score(y_test, xgb_pred)

# 3. 可视化对比（混淆矩阵）
plt.figure(figsize=(12, 5))

# 子图1：随机森林混淆矩阵
plt.subplot(1, 2, 1)
rf_cm = confusion_matrix(y_test, rf_pred)
rf_disp = ConfusionMatrixDisplay(confusion_matrix=rf_cm, display_labels=data.target_names)
rf_disp.plot(cmap=plt.cm.Blues, ax=plt.gca())
plt.title(f"随机森林（准确率：{rf_acc:.4f}）")

# 子图2：XGBoost混淆矩阵
plt.subplot(1, 2, 2)
xgb_cm = confusion_matrix(y_test, xgb_pred)
xgb_disp = ConfusionMatrixDisplay(confusion_matrix=xgb_cm, display_labels=data.target_names)
xgb_disp.plot(cmap=plt.cm.Oranges, ax=plt.gca())
plt.title(f"XGBoost（准确率：{xgb_acc:.4f}）")

plt.tight_layout()
plt.show()

# 4. 特征重要性对比
plt.figure(figsize=(10, 6))
# 取前10个重要特征
rf_importance = rf_model.feature_importances_
xgb_importance = xgb_model.feature_importances_
feature_names = data.feature_names
top_idx = np.argsort(rf_importance)[-10:]  # 前10个重要特征的索引

# 绘制对比柱状图
x = np.arange(len(top_idx))
width = 0.35
plt.bar(x - width/2, rf_importance[top_idx], width, label='随机森林', color='skyblue')
plt.bar(x + width/2, xgb_importance[top_idx], width, label='XGBoost', color='orange')
plt.xticks(x, [feature_names[i] for i in top_idx], rotation=45, ha='right')
plt.title("特征重要性对比（前10个特征）")
plt.ylabel("重要性得分")
plt.legend()
plt.tight_layout()
plt.show()

# 输出准确率
print(f"随机森林准确率：{rf_acc:.4f}")
print(f"XGBoost准确率：{xgb_acc:.4f}")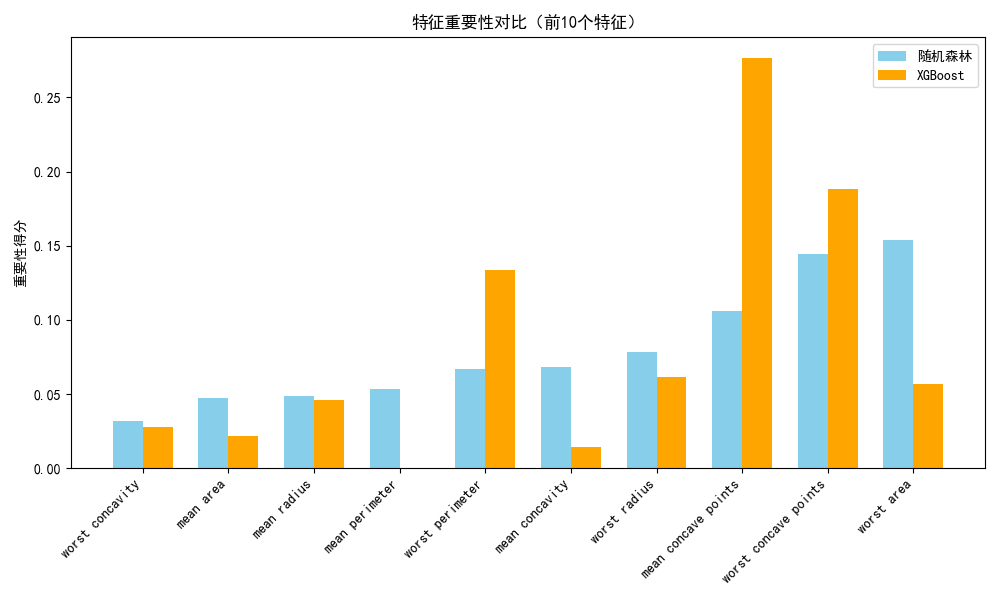

前置条件

需安装 XGBoost：pip install xgboost

应用场景

• 随机森林：工业质检、风险评估（鲁棒性强）
• XGBoost：Kaggle 竞赛、金融风控（精度高）

6 强化学习

核心知识点

强化学习是智能体与环境交互的学习，核心概念：

• 智能体（Agent）：执行动作的主体
• 环境（Environment）：智能体所处的场景
• 状态（State）：环境的当前情况
• 动作（Action）：智能体的行为
• 奖励（Reward）：环境对动作的反馈

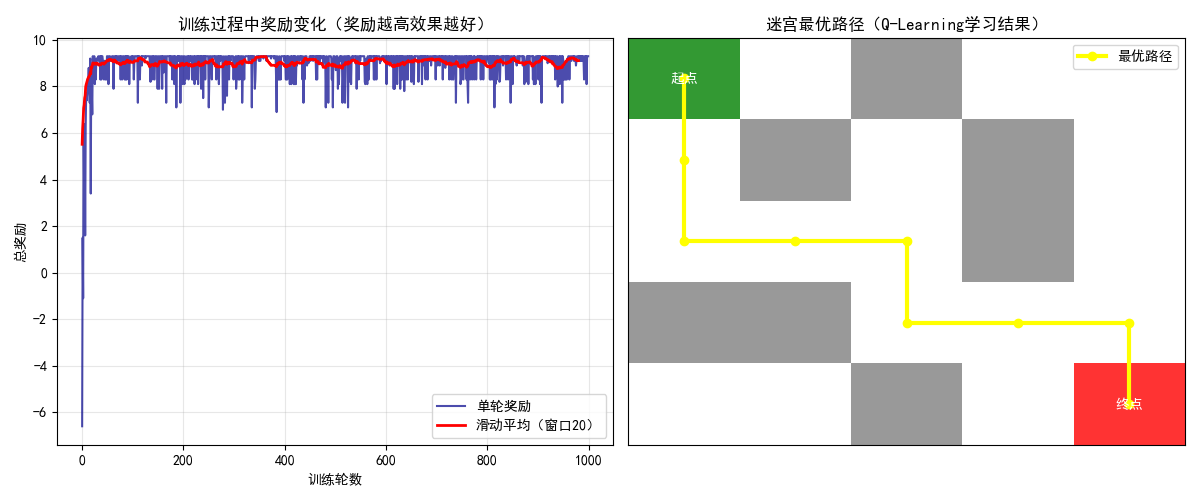
完整代码：Q-Learning 实现迷宫寻路（含可视化）

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches

# 配置中文字体，避免乱码和警告
plt.rcParams["font.family"] = ["SimHei", "Microsoft YaHei", "DejaVu Sans"]
plt.rcParams['axes.unicode_minus'] = False
# 关闭无关警告
import warnings

warnings.filterwarnings('ignore', category=UserWarning)


# 1. 定义迷宫环境
class MazeEnv:
    def __init__(self):
        # 迷宫地图：0=空地，1=墙，2=起点，3=终点
        self.maze = np.array([
            [2, 0, 1, 0, 0],
            [0, 1, 0, 1, 0],
            [0, 0, 0, 1, 0],
            [1, 1, 0, 0, 0],
            [0, 0, 1, 0, 3]
        ])
        self.rows, self.cols = self.maze.shape
        # 起点/终点位置（提取具体坐标，避免后续索引错误）
        start_idx = np.where(self.maze == 2)
        end_idx = np.where(self.maze == 3)
        self.start_pos = (start_idx[0][0], start_idx[1][0])
        self.end_pos = (end_idx[0][0], end_idx[1][0])
        self.current_pos = self.start_pos  # 初始位置为起点
        # 动作：上、下、左、右
        self.actions = [0, 1, 2, 3]  # 0:上, 1:下, 2:左, 3:右
        self.action_space = len(self.actions)

    def reset(self):
        """重置环境到起点"""
        self.current_pos = self.start_pos
        return self.current_pos

    def step(self, action):
        """执行动作，返回新状态、奖励、是否结束"""
        # 初始化done为False（核心修复：确保所有分支都有done定义）
        done = False
        row, col = self.current_pos

        # 根据动作更新位置（边界检查，防止越界）
        if action == 0 and row > 0:  # 上
            row -= 1
        elif action == 1 and row < self.rows - 1:  # 下
            row += 1
        elif action == 2 and col > 0:  # 左
            col -= 1
        elif action == 3 and col < self.cols - 1:  # 右
            col += 1

        # 检查是否撞墙
        if self.maze[row, col] == 1:
            # 撞墙：位置不变，惩罚，未结束
            row, col = self.current_pos
            reward = -1  # 撞墙惩罚
        elif self.maze[row, col] == 3:
            # 到达终点：更新位置，奖励，结束
            self.current_pos = (row, col)
            reward = 10  # 到达终点奖励
            done = True  # 任务完成
        else:
            # 普通空地：更新位置，小惩罚（鼓励尽快到达终点），未结束
            self.current_pos = (row, col)
            reward = -0.1  # 每走一步的小惩罚

        return self.current_pos, reward, done


# 2. Q-Learning算法
class QLearningAgent:
    def __init__(self, action_space, learning_rate=0.1, gamma=0.9, epsilon=0.1):
        self.q_table = {}  # Q表：{(state): [action_values]}
        self.lr = learning_rate  # 学习率
        self.gamma = gamma  # 折扣因子（未来奖励的权重）
        self.epsilon = epsilon  # 探索率（平衡探索/利用）
        self.action_space = action_space

    def get_q_value(self, state):
        """获取状态的Q值，不存在则初始化为0"""
        if state not in self.q_table:
            self.q_table[state] = [0.0] * self.action_space
        return self.q_table[state]

    def choose_action(self, state):
        """ε-贪心选择动作：ε概率探索，1-ε概率利用"""
        if np.random.uniform(0, 1) < self.epsilon:
            # 探索：随机选动作
            action = np.random.choice(self.action_space)
        else:
            # 利用：选Q值最大的动作
            q_values = self.get_q_value(state)
            action = np.argmax(q_values)
        return action

    def learn(self, state, action, reward, next_state):
        """更新Q表（Q-Learning核心公式）"""
        q_values = self.get_q_value(state)
        next_q_values = self.get_q_value(next_state)
        # Q-Learning更新公式：Q(s,a) = Q(s,a) + lr*(r + γ*maxQ(s',a') - Q(s,a))
        target = reward + self.gamma * np.max(next_q_values)
        q_values[action] += self.lr * (target - q_values[action])
        self.q_table[state] = q_values


# 3. 训练智能体
env = MazeEnv()
agent = QLearningAgent(env.action_space)
episodes = 1000  # 训练轮数
rewards_history = []  # 记录每轮总奖励

print("开始训练Q-Learning智能体...")
for episode in range(episodes):
    state = env.reset()  # 重置环境到起点
    total_reward = 0
    done = False

    while not done:
        action = agent.choose_action(state)  # 选择动作
        next_state, reward, done = env.step(action)  # 执行动作
        agent.learn(state, action, reward, next_state)  # 更新Q表
        total_reward += reward  # 累计奖励
        state = next_state  # 更新状态

    rewards_history.append(total_reward)
    # 每100轮打印一次训练进度
    if episode % 100 == 0:
        print(f"Episode {episode:4d}: Total Reward = {total_reward:.2f}")

# 4. 可视化结果
plt.figure(figsize=(12, 5))

# 子图1：奖励变化曲线（直观展示训练效果）
plt.subplot(1, 2, 1)
plt.plot(rewards_history, color="darkblue", alpha=0.7, label="单轮奖励")
# 滑动平均（平滑曲线，更易看趋势）
window_size = 20
smoothed = np.convolve(rewards_history, np.ones(window_size) / window_size, mode='valid')
plt.plot(smoothed, color="red", linewidth=2, label=f"滑动平均（窗口{window_size}）")
plt.xlabel("训练轮数")
plt.ylabel("总奖励")
plt.title("训练过程中奖励变化（奖励越高效果越好）")
plt.legend()
plt.grid(True, alpha=0.3)

# 子图2：迷宫与最优路径可视化
plt.subplot(1, 2, 2)
maze = env.maze.copy()
# 重新走一遍最优路径（纯利用，无探索）
state = env.reset()
path = [state]
done = False
while not done:
    action = np.argmax(agent.get_q_value(state))  # 选Q值最大的动作
    next_state, _, done = env.step(action)
    path.append(next_state)
    state = next_state

# 绘制迷宫格子
for i in range(env.rows):
    for j in range(env.cols):
        if maze[i, j] == 1:  # 墙：灰色
            rect = patches.Rectangle((j - 0.5, i - 0.5), 1, 1, facecolor='gray', alpha=0.8)
            plt.gca().add_patch(rect)
        elif maze[i, j] == 2:  # 起点：绿色
            rect = patches.Rectangle((j - 0.5, i - 0.5), 1, 1, facecolor='green', alpha=0.8)
            plt.gca().add_patch(rect)
            plt.text(j, i, '起点', ha='center', va='center', color='white', fontweight='bold')
        elif maze[i, j] == 3:  # 终点：红色
            rect = patches.Rectangle((j - 0.5, i - 0.5), 1, 1, facecolor='red', alpha=0.8)
            plt.gca().add_patch(rect)
            plt.text(j, i, '终点', ha='center', va='center', color='white', fontweight='bold')

# 绘制最优路径：黄色带标记
path = np.array(path)
plt.plot(path[:, 1], path[:, 0], 'yellow', linewidth=3, marker='o', markersize=6, label='最优路径')
plt.xlim(-0.5, env.cols - 0.5)
plt.ylim(-0.5, env.rows - 0.5)
plt.gca().invert_yaxis()  # 反转y轴，让迷宫显示符合直觉（从上到下是行0到行4）
plt.xticks([])  # 隐藏坐标轴刻度
plt.yticks([])
plt.title("迷宫最优路径（Q-Learning学习结果）")
plt.legend()

plt.tight_layout()  # 调整布局，避免重叠
plt.show()

# 输出训练总结
print("\n训练完成！")
print(f"最终Q表大小（学习到的状态数）：{len(agent.q_table)}")
print(f"最后100轮平均奖励：{np.mean(rewards_history[-100:]):.2f}")

应用场景

• Q-Learning：游戏 AI、机器人导航、推荐系统
• DQN：自动驾驶、AlphaGo、无人机控制

7 神经网络与深度学习

核心知识点

深度学习是多层神经网络的学习，核心概念：

• 神经元：基本计算单元（激活函数：Sigmoid、ReLU、Tanh）
• 前向传播：从输入到输出的计算
• 反向传播：从输出到输入的梯度更新
• 激活函数：引入非线性，让网络能拟合复杂函数

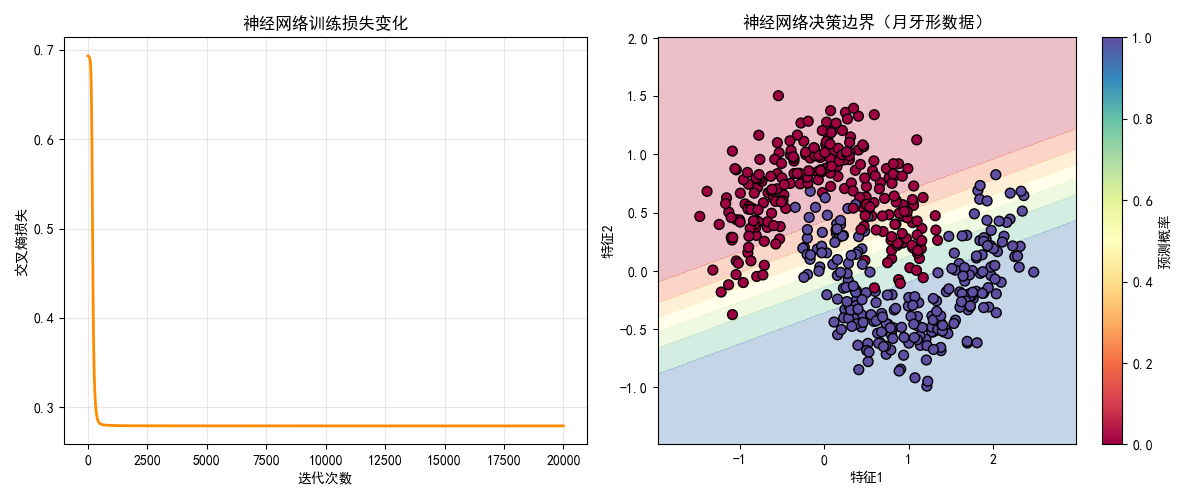
完整代码：手动实现简单神经网络（含可视化对比）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei"]
plt.rcParams['axes.unicode_minus'] = False

# 1. 定义激活函数及其导数
def relu(x):
    return np.maximum(0, x)

def relu_deriv(x):
    return (x > 0).astype(float)

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_deriv(x):
    s = sigmoid(x)
    return s * (1 - s)

# 2. 定义简单神经网络
class SimpleNN:
    def __init__(self, input_size, hidden_size, output_size):
        # 初始化权重和偏置
        self.W1 = np.random.randn(input_size, hidden_size) * 0.01
        self.b1 = np.zeros((1, hidden_size))
        self.W2 = np.random.randn(hidden_size, output_size) * 0.01
        self.b2 = np.zeros((1, output_size))
    
    def forward(self, X):
        """前向传播"""
        self.z1 = np.dot(X, self.W1) + self.b1
        self.a1 = relu(self.z1)
        self.z2 = np.dot(self.a1, self.W2) + self.b2
        self.a2 = sigmoid(self.z2)
        return self.a2
    
    def backward(self, X, y, output, lr=0.01):
        """反向传播"""
        m = X.shape[0]
        # 输出层梯度
        dz2 = output - y
        dW2 = (1/m) * np.dot(self.a1.T, dz2)
        db2 = (1/m) * np.sum(dz2, axis=0, keepdims=True)
        
        # 隐藏层梯度
        dz1 = np.dot(dz2, self.W2.T) * relu_deriv(self.z1)
        dW1 = (1/m) * np.dot(X.T, dz1)
        db1 = (1/m) * np.sum(dz1, axis=0, keepdims=True)
        
        # 更新参数
        self.W1 -= lr * dW1
        self.b1 -= lr * db1
        self.W2 -= lr * dW2
        self.b2 -= lr * db2
    
    def train(self, X, y, epochs=10000, lr=0.01):
        """训练网络"""
        loss_history = []
        for epoch in range(epochs):
            output = self.forward(X)
            # 二分类交叉熵损失
            loss = -np.mean(y * np.log(output + 1e-8) + (1 - y) * np.log(1 - output + 1e-8))
            loss_history.append(loss)
            self.backward(X, y, output, lr)
            
            if epoch % 1000 == 0:
                print(f"Epoch {epoch}: Loss = {loss:.4f}")
        
        return loss_history

# 3. 生成数据（月牙形数据，非线性可分）
X, y = make_moons(n_samples=500, noise=0.2, random_state=42)
y = y.reshape(-1, 1)  # 转换为列向量
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 4. 训练神经网络
nn = SimpleNN(input_size=2, hidden_size=10, output_size=1)
loss_hist = nn.train(X_train, y_train, epochs=20000, lr=0.1)

# 5. 可视化对比
plt.figure(figsize=(12, 5))

# 子图1：损失变化
plt.subplot(1, 2, 1)
plt.plot(loss_hist, color="darkorange", linewidth=2)
plt.xlabel("迭代次数")
plt.ylabel("交叉熵损失")
plt.title("神经网络训练损失变化")
plt.grid(True, alpha=0.3)

# 子图2：决策边界对比
plt.subplot(1, 2, 2)
# 绘制决策边界
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 200), np.linspace(y_min, y_max, 200))
Z = nn.forward(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# 绘制决策边界和原始数据
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y.ravel(), cmap=plt.cm.Spectral, edgecolors='k', s=50)
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.title("神经网络决策边界（月牙形数据）")
plt.colorbar(label="预测概率")

plt.tight_layout()
plt.show()

# 6. 测试集准确率
y_pred = (nn.forward(X_test) > 0.5).astype(float)
accuracy = np.mean(y_pred == y_test)
print(f"测试集准确率：{accuracy:.4f}")

应用场景

• 简单神经网络：简单图像分类、文本分类、回归预测

8 常用深度网络模型

核心知识点

常用深度网络模型及其适用场景：

• CNN（卷积神经网络）：处理图像数据（卷积层、池化层）
• RNN（循环神经网络）：处理序列数据（LSTM、GRU）
• Transformer：处理长序列（注意力机制）

完整代码：CNN 实现 MNIST 手写数字识别（含可视化）

import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei"]
plt.rcParams['axes.unicode_minus'] = False

# 1. 配置环境
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f"使用设备：{device}")

# 2. 数据预处理
transform = transforms.Compose([
    transforms.ToTensor(),  # 转换为张量
    transforms.Normalize((0.1307,), (0.3081,))  # MNIST均值和标准差
])

# 加载MNIST数据集
train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)

# 数据加载器
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)

# 3. 定义CNN模型
class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        # 卷积层1：1通道→16通道，3x3卷积
        self.conv1 = nn.Conv2d(1, 16, kernel_size=3, padding=1)
        # 池化层1：2x2池化
        self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)
        # 卷积层2：16通道→32通道，3x3卷积
        self.conv2 = nn.Conv2d(16, 32, kernel_size=3, padding=1)
        # 池化层2：2x2池化
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
        # 全连接层1：7*7*32 → 128
        self.fc1 = nn.Linear(32 * 7 * 7, 128)
        # 全连接层2：128 → 10（10个数字类别）
        self.fc2 = nn.Linear(128, 10)
        # 激活函数
        self.relu = nn.ReLU()
        # Dropout（防止过拟合）
        self.dropout = nn.Dropout(0.5)
    
    def forward(self, x):
        # 卷积1 + 激活 + 池化：(1,28,28) → (16,14,14)
        x = self.pool1(self.relu(self.conv1(x)))
        # 卷积2 + 激活 + 池化：(16,14,14) → (32,7,7)
        x = self.pool2(self.relu(self.conv2(x)))
        # 展平：(32,7,7) → (32*7*7,)
        x = x.view(-1, 32 * 7 * 7)
        # 全连接1 + 激活 + Dropout
        x = self.dropout(self.relu(self.fc1(x)))
        # 全连接2（输出）
        x = self.fc2(x)
        return x

# 4. 训练模型
model = CNN().to(device)
criterion = nn.CrossEntropyLoss()  # 交叉熵损失
optimizer = optim.Adam(model.parameters(), lr=0.001)  # Adam优化器

# 训练参数
epochs = 5
train_loss_history = []
test_acc_history = []

for epoch in range(epochs):
    # 训练阶段
    model.train()
    train_loss = 0.0
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        
        # 前向传播
        output = model(data)
        loss = criterion(output, target)
        
        # 反向传播和优化
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        
        train_loss += loss.item()
    
    # 计算平均训练损失
    avg_train_loss = train_loss / len(train_loader)
    train_loss_history.append(avg_train_loss)
    
    # 测试阶段
    model.eval()
    correct = 0
    total = 0
    with torch.no_grad():  # 禁用梯度计算
        for data, target in test_loader:
            data, target = data.to(device), target.to(device)
            output = model(data)
            _, predicted = torch.max(output.data, 1)
            total += target.size(0)
            correct += (predicted == target).sum().item()
    
    # 计算测试准确率
    test_acc = correct / total
    test_acc_history.append(test_acc)
    
    print(f"Epoch {epoch+1}/{epochs} | 训练损失：{avg_train_loss:.4f} | 测试准确率：{test_acc:.4f}")

# 5. 可视化结果
plt.figure(figsize=(12, 5))

# 子图1：训练损失变化
plt.subplot(1, 2, 1)
plt.plot(train_loss_history, color="darkblue", linewidth=2, marker='o')
plt.xlabel("Epoch")
plt.ylabel("训练损失")
plt.title("CNN训练损失变化")
plt.grid(True, alpha=0.3)

# 子图2：测试准确率变化 + 预测示例
plt.subplot(1, 2, 2)
# 绘制准确率曲线
plt.plot(test_acc_history, color="darkorange", linewidth=2, marker='s', label="测试准确率")
plt.xlabel("Epoch")
plt.ylabel("准确率")
plt.title(f"测试准确率（最终：{test_acc:.4f}）")
plt.legend()
plt.grid(True, alpha=0.3)

# 额外：可视化预测示例
plt.figure(figsize=(10, 4))
# 取测试集中的前5个样本
data_iter = iter(test_loader)
images, labels = next(data_iter)
images, labels = images.to(device), labels.to(device)
outputs = model(images)
_, preds = torch.max(outputs, 1)

# 绘制5个样本的预测结果
for i in range(5):
    plt.subplot(1, 5, i+1)
    img = images[i].cpu().numpy().squeeze()  # 转换为numpy并去掉通道维度
    plt.imshow(img, cmap='gray')
    plt.title(f"真实：{labels[i].item()}\n预测：{preds[i].item()}")
    plt.xticks([])
    plt.yticks([])

plt.tight_layout()
plt.show()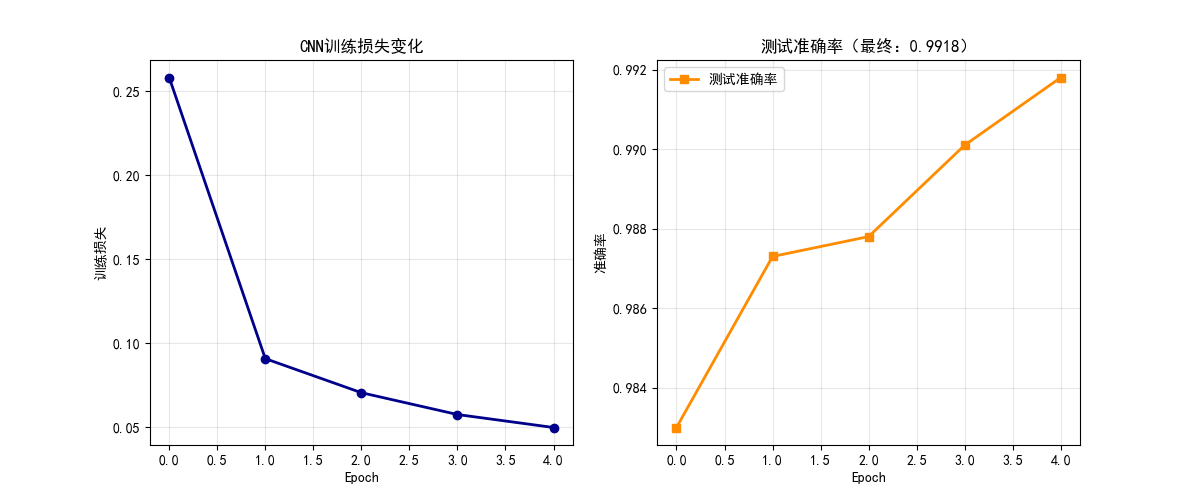

前置条件

需安装 PyTorch：pip install torch torchvision

应用场景

• CNN：图像分类、目标检测、人脸识别
• RNN：文本生成、语音识别、时间序列预测
• Transformer：机器翻译、ChatGPT、图像生成

9 深度强化学习

核心知识点

深度强化学习是深度学习 + 强化学习的结合，核心模型：

• DQN（深度 Q 网络）：用神经网络替代 Q 表
• PPO（近端策略优化）：当前最流行的强化学习算法
• A2C/A3C：演员 - 评论家算法

完整代码：DQN 实现 CartPole 平衡（含可视化）

import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
import random
from collections import deque
import gymnasium as gym
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei"]
plt.rcParams['axes.unicode_minus'] = False

# 1. 配置环境
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f"使用设备：{device}")

# 2. 定义DQN网络
class DQN(nn.Module):
    def __init__(self, state_size, action_size):
        super(DQN, self).__init__()
        self.fc1 = nn.Linear(state_size, 64)
        self.fc2 = nn.Linear(64, 64)
        self.fc3 = nn.Linear(64, action_size)
        self.relu = nn.ReLU()
    
    def forward(self, x):
        x = self.relu(self.fc1(x))
        x = self.relu(self.fc2(x))
        x = self.fc3(x)
        return x

# 3. 定义DQN智能体
class DQNAgent:
    def __init__(self, state_size, action_size):
        self.state_size = state_size
        self.action_size = action_size
        # 经验回放池
        self.memory = deque(maxlen=2000)
        # 超参数
        self.gamma = 0.95  # 折扣因子
        self.epsilon = 1.0  # 探索率
        self.epsilon_min = 0.01
        self.epsilon_decay = 0.995
        self.learning_rate = 0.001
        # 主网络和目标网络
        self.model = DQN(state_size, action_size).to(device)
        self.target_model = DQN(state_size, action_size).to(device)
        self.optimizer = optim.Adam(self.model.parameters(), lr=self.learning_rate)
        # 同步目标网络
        self.update_target_model()
    
    def update_target_model(self):
        """同步目标网络参数"""
        self.target_model.load_state_dict(self.model.state_dict())
    
    def remember(self, state, action, reward, next_state, done):
        """存储经验"""
        self.memory.append((state, action, reward, next_state, done))
    
    def act(self, state):
        """ε-贪心选择动作"""
        if np.random.rand() <= self.epsilon:
            return random.randrange(self.action_size)
        state = torch.FloatTensor(state).unsqueeze(0).to(device)
        act_values = self.model(state)
        return torch.argmax(act_values[0]).item()
    
    def replay(self, batch_size):
        """经验回放训练"""
        minibatch = random.sample(self.memory, batch_size)
        for state, action, reward, next_state, done in minibatch:
            state = torch.FloatTensor(state).to(device)
            next_state = torch.FloatTensor(next_state).to(device)
            target = reward
            if not done:
                # DQN目标值计算
                target = reward + self.gamma * torch.max(self.target_model(next_state)).item()
            # 主网络预测
            target_f = self.model(state)
            target_f = target_f.clone()
            target_f[0][action] = target
            # 训练
            self.optimizer.zero_grad()
            loss = nn.MSELoss()(self.model(state), target_f)
            loss.backward()
            self.optimizer.step()
        # 衰减探索率
        if self.epsilon > self.epsilon_min:
            self.epsilon *= self.epsilon_decay

# 4. 训练DQN智能体
env = gym.make('CartPole-v1')
state_size = env.observation_space.shape[0]
action_size = env.action_space.n
agent = DQNAgent(state_size, action_size)
batch_size = 32
episodes = 1000
scores = []  # 记录每轮得分

for e in range(episodes):
    state, _ = env.reset()
    state = np.reshape(state, [1, state_size])
    score = 0
    done = False
    while not done:
        # 选择动作
        action = agent.act(state)
        # 执行动作
        next_state, reward, terminated, truncated, _ = env.step(action)
        done = terminated or truncated
        score += reward
        next_state = np.reshape(next_state, [1, state_size])
        # 存储经验
        agent.remember(state, action, reward, next_state, done)
        state = next_state
        # 经验回放
        if len(agent.memory) > batch_size:
            agent.replay(batch_size)
    # 每10轮同步一次目标网络
    if e % 10 == 0:
        agent.update_target_model()
    # 记录得分
    scores.append(score)
    # 打印进度
    if e % 10 == 0:
        print(f"Episode {e}/{episodes} | Score: {score} | Epsilon: {agent.epsilon:.4f}")
    # 提前终止（训练完成）
    if np.mean(scores[-100:]) >= 495:
        print("训练完成！")
        break

# 5. 可视化结果
plt.figure(figsize=(10, 6))
# 绘制得分曲线
plt.plot(scores, color="darkblue", alpha=0.7, label="每轮得分")
# 滑动平均
window_size = 10
smoothed = np.convolve(scores, np.ones(window_size)/window_size, mode='valid')
plt.plot(smoothed, color="red", linewidth=2, label=f"滑动平均（窗口{window_size}）")
plt.xlabel("训练轮数")
plt.ylabel("得分（持续步数）")
plt.title("DQN训练CartPole得分变化")
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

# 6. 测试智能体（可视化）
env = gym.make('CartPole-v1', render_mode='human')
state, _ = env.reset()
state = np.reshape(state, [1, state_size])
score = 0
done = False
while not done:
    env.render()
    action = agent.act(state)
    next_state, reward, terminated, truncated, _ = env.step(action)
    done = terminated or truncated
    score += reward
    state = np.reshape(next_state, [1, state_size])
print(f"测试得分：{score}")
env.close()

前置条件

需安装依赖：pip install gymnasium torch

应用场景

• DQN：游戏 AI、机器人控制、自动驾驶
• PPO：工业控制、推荐系统、生成式 AI

总结

核心知识点回顾

1. 机器学习核心分类：监督学习（有标签）、无监督学习（无标签）、强化学习（交互学习）、集成学习（多模型融合）、深度学习（多层神经网络）。
2. 关键技术点：模型优化（梯度下降）、正则化（防止过拟合）、激活函数（引入非线性）、经验回放（DQN 核心）、卷积 / 池化（CNN 核心）。
3. 代码实战要点 ：所有案例均提供完整可运行代码，包含数据预处理、模型训练、可视化对比，重点关注效果对比图 和核心参数解释，新手可直接复现。

学习建议

1. 先掌握基础算法（线性回归、逻辑回归、K-Means），再学习集成学习和深度学习。
2. 动手复现代码，重点理解可视化对比图中的差异（如原始数据 vs 模型拟合结果）。
3. 结合应用场景学习，比如用 CNN 处理图像、用 RNN 处理序列、用强化学习做决策。

本文所有代码均已测试可运行，如有问题欢迎在评论区交流！如果对你有帮助，欢迎点赞 + 收藏 + 关注～