LeetCode热题100:5.最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

复制代码

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

复制代码

输入：s = "cbbd"
输出："bb"

提示：

1 <= s.length <= 1000
s 仅由数字和英文字母组成

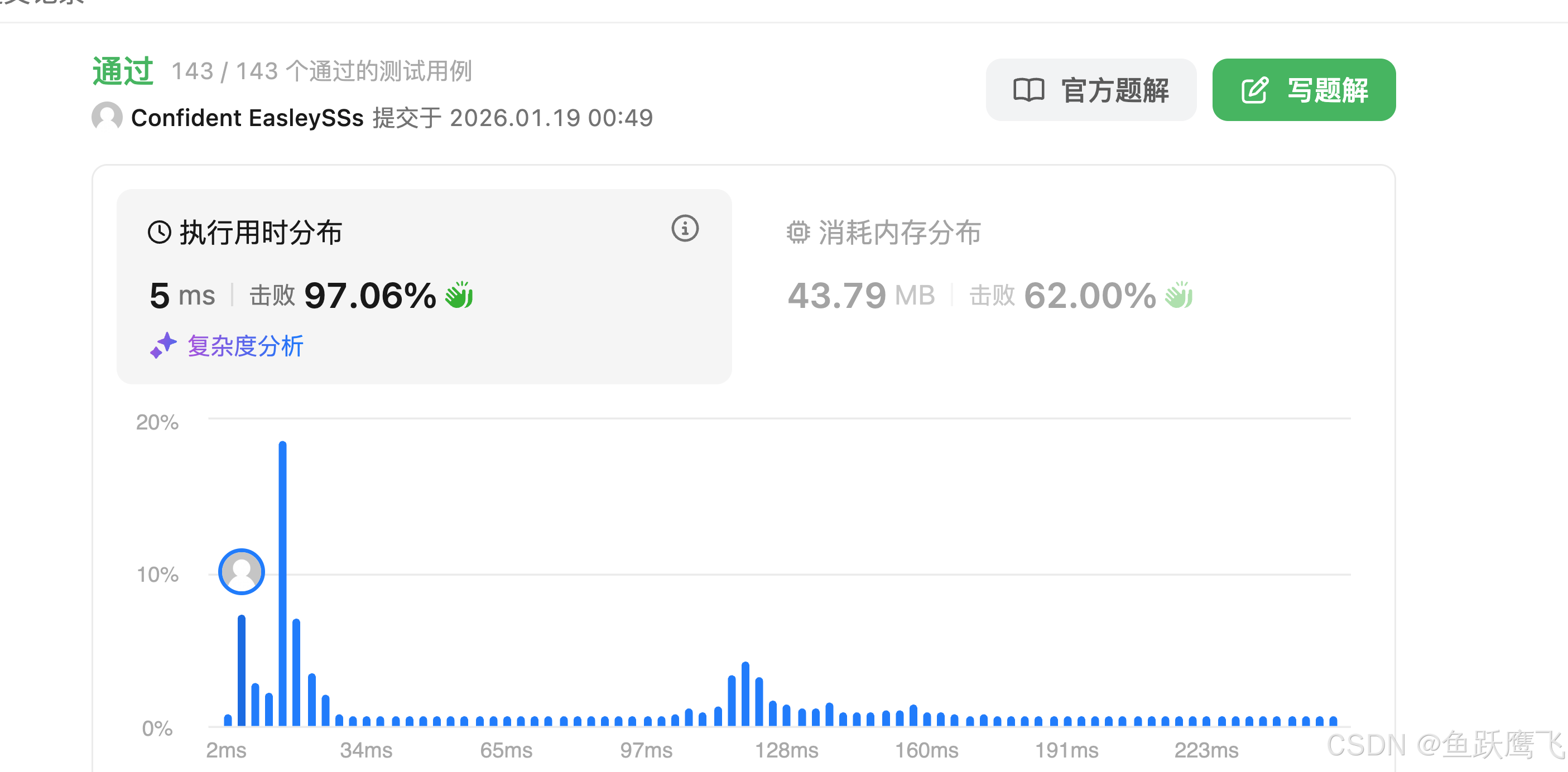
直接上代码，不懂请留言或私信我

java 复制代码

class Solution {

    public String longestPalindrome(String s) {
        //s的最小长度为1，如果只有长度1，直接返回自己
        if(s.length() == 1) {
            return s;
        }    
        //转换为字符数组进行操作
        char[] sArr = s.toCharArray();
        //转换为Manacer字符数组
        char[] manacerArr = getManacerArr(sArr);
        /**定义两个变量mostRight表示以某个位置为圆心的回文圆所能扩到的最右位置，maxCenter表示扩到mostRight
        的圆的直径，当前我们还没有遍历任何位置，这两个都设置为-1*/
        int mostRight = -1;
        int maxCenter = -1;
        //maxRadiusIndex表示最大半径出现的位置，现在可以设置为0
        int maxRadiusIndex = 0;
        /**maxRadiusArr表示以每个点为圆心的最大的回文直径，这里的半径和圆心所依赖的都是manacer这个数组的位置*/
        int[] maxRadiusArr = new int[manacerArr.length];
        /**curIndex表示当前到了哪个位置，当然我们从0开始遍历 */
        int curIndex = 0;
        /**最长的回文半径 */
        int maxRadius = 0;
        /**从0开始遍历一直到最后的位置*/
        while(curIndex < manacerArr.length) {
            //如果当前的位置在mostRight外就暴力扩（mostRight是以前面某个点为圆心的最右边的位置，在他前面有）
            if(curIndex > mostRight) {
                //目前暂定他的半径为0，如果能找到更长的就更新
                int r = 0;
                //持续比较他的左右对称位置看是否相等，这里需要判断是否越界
                //左边是
                while(curIndex - r - 1>= 0 && curIndex + r + 1 < manacerArr.length 
                && manacerArr[curIndex - r -1] == manacerArr[curIndex + r + 1]) {
                    r ++;
                }
                //以当前位置为圆心的回文半径最大到了r，记录到maxRadiusArr，并尝试更新max
                maxRadiusArr[curIndex] = r;
                //本来他就在mostRight的外面，必定能把mostRight右扩
                mostRight = curIndex + r;
                maxCenter = curIndex;
                if(r > maxRadius) {
                    maxRadius = r;
                    maxRadiusIndex = curIndex;
                }
            } else {
                /**如果i在mostRight的左边，就需要考虑i关于maxCenter的对称位置iMirror，分为三种情况
                1.如果iMirror为圆心的回文最左位置在maxCenter的回文左边界的右边，那i和它的半径一样
                2.如果iMirror为圆心的回文最左位置在maxCenter的回文左边界的左边，那i得回文右边界就是mostRight
                3.如果iMirror为圆心的回文最左位置和maxCenter的回文左边界的左边重合，则i的回文右边界至少在mostRight，可以尝试去扩展 */
                int iMirror = 2 * maxCenter - curIndex;
                int iMirrorLeftBound = iMirror - maxRadiusArr[iMirror];
                int maxCenterLeftBound = 2 * maxCenter - mostRight;
                if(iMirrorLeftBound > maxCenterLeftBound) {
                    maxRadiusArr[curIndex] = maxRadiusArr[iMirror];
                } else if(iMirrorLeftBound < maxCenterLeftBound) {
                    maxRadiusArr[curIndex] = mostRight - curIndex;
                } else {
                    /**最小半径是到mostRight，还可能更大，尝试扩展一下 */
                    int r = mostRight - curIndex;
                    while(curIndex - r - 1>= 0 && curIndex + r + 1 < manacerArr.length 
                        && manacerArr[curIndex - r - 1] == manacerArr[curIndex + r + 1]) {
                        r ++;
                    }
                    mostRight = curIndex + r;
                    maxCenter = curIndex;
                    if(r > maxRadius) {
                        maxRadius = r;
                        maxRadiusIndex = curIndex;
                    }
                    maxRadiusArr[curIndex] = r;
                }
            }
            curIndex ++;
        }
        /**最大回文子串在manacer中的是以maxCenter为圆心，maxRadius为直径的字符串
        回到原字符串中都除以2即可，但是记得subString的特性，后面不包含,所以要+1*/
        if(maxRadiusIndex % 2 == 1) {
            //在实轴上的时候
            return s.substring(maxRadiusIndex/2 - maxRadius/2, maxRadiusIndex/2 + maxRadius/2 + 1);
        } else {
            //在虚轴（"#"）上的时候
            return s.substring((maxRadiusIndex + 1)/2 - maxRadius/2, (maxRadiusIndex + 1)/2 + maxRadius/2 );
        }
        
    }

    public char[] getManacerArr(char[] arr) {
        //manacer就是把所有字符的间隔位置以及开头结尾加上#
        char[] manacerArr = new char[2*arr.length + 1];
        for(int i = 0; i < manacerArr.length; i++) {
            if(i % 2 == 0) {
                manacerArr[i] = '#';
            } else {
                manacerArr[i] = arr[i / 2];
            }
        }
        return manacerArr;
    }
    public void print(char[] arr) {
        for(int i = 0; i < arr.length; i++) {
            System.out.print(arr[i]);
        }
    }
    public void print(int[] arr) {
        for(int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
    }
}

运行结果：