洛谷P7224 [RC-04] 子集积解析

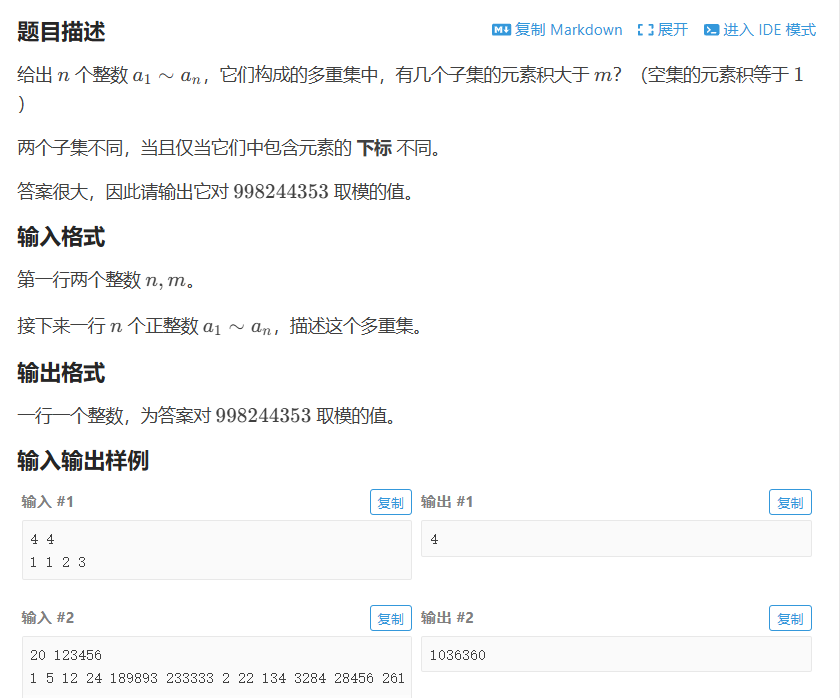
首先看数据范围

n小于等于22，无脑dfs一顿混个基础分

cpp 复制代码

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e6 + 5;
const int mod = 998244353;
LL n, m, a[maxn], ans;
void dfs(LL s, int x) {
	for (int i = x; i <= n; ++i) {
		s *= a[i];
		if (s > m)ans = (ans + 1) % mod;
		dfs(s, i + 1);
		s /= a[i];
	}
}
int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; ++i)cin >> a[i];
	dfs(1, 1);
	cout << ans;
	return 0;
}

出题人真心好！65分！剩下超时！

再看题意？

求子集积大于m的子集个数？

大于m的个数不好用背包，小于等于用背包就好求嘛！正难则反！正难则反！正难则反！

最后用2^n减去就可以

分析答案：对于一个子集积小于等于m的子集来说，必定包含了某几个数，那么对于所有的数来说，存在选与不选两种情况，妥妥的01背包。

物品：数背包容量：m

转移方程：f $j$ =f $j$ +f $j/a\[ i$ ]

初始值：f $1$ =1

意为目前子集积为1的只有空集，其它选择情况都可以从空集转移

不对啊

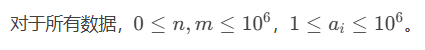
第二层循环 j从m到a $i$ 必定会超时

不管，先打了再说

cpp 复制代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 1e6 + 5;
const int mod = 998244353;
int n, m, a[maxn], ans;
int f[maxn]; //f[j]表示前i个数的积等于j方案数
int ksm(int x, int y) {
	int rtn = 1;
	while (y) {
		if (y & 1)rtn = rtn * x % mod;
		x = x * x % mod;
		y >>= 1;
	}
	return rtn;
}
signed main() {
	cin >> n >> m;
	for (int i = 1; i <= n; ++i)cin >> a[i];
	f[1] = 1;
	for (int i = 1; i <= n; ++i) {
		for (int j = m; j >= a[i]; --j) {//用此法只有34分
			if (j % a[i] == 0)f[j] = (f[j] + f[j / a[i]]) % mod;
//		for (int j = m / a[i] * a[i]; j > 0; j -= a[i]) {//用此法有55分
//			f[j] = (f[j] + f[j / a[i]]) % mod;
		}
	}
	int ans = ksm(2, n);
	for (int i = 1; i <= m; ++i)ans = (ans - f[i] + mod) % mod;
	cout << ans;
	return 0;
}

34分

观察对于当前数a $i$ 来说，只有j%a $i$ ==0的才能转移，

怒优化为：for (int j=m/a $i$ *a $i$ ;j>0;j-=a $i$ )

55分

再看数据范围

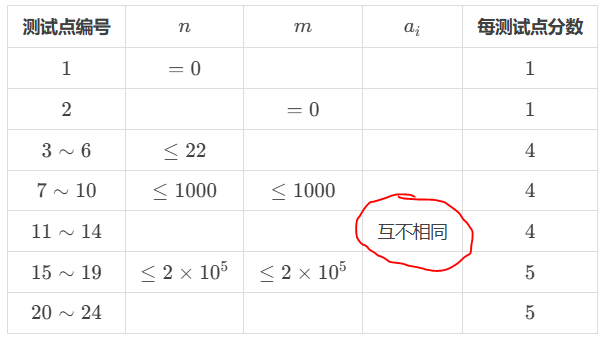
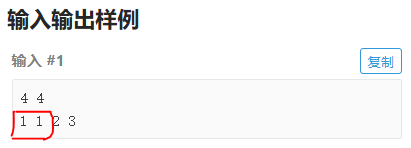
发现什么了吗？

对！有相同数，可以预料的是可能有很多相同数！

分析样例：1 1 2 3中有两个1，去掉重复的1后剩下 1 2 3，满足要求的子集是{1}{2}{3}{12}{13}共5个，如果再加上一个1，则答案变成2*5，再加一个1，2*2*5,......。