DARTS#01 | Tournament Sort算法 | MySQL深度翻页优化技巧

DARTS#01 | Tournament Sort算法 | MySQL深度翻页优化技巧 | 论文ByteSlice Review

Tournament Sort在数据库中的应用

Tournament sort（锦标赛排序/淘汰赛排序）

用途：一种外排序算法（归并排序），它的好处是能在相同的内存约束情况下，产生更少的IO，代价是内存中的计算会更多，适用于内存有限情况下的大规模数据的排序，或者有序度较高的数据集排序。

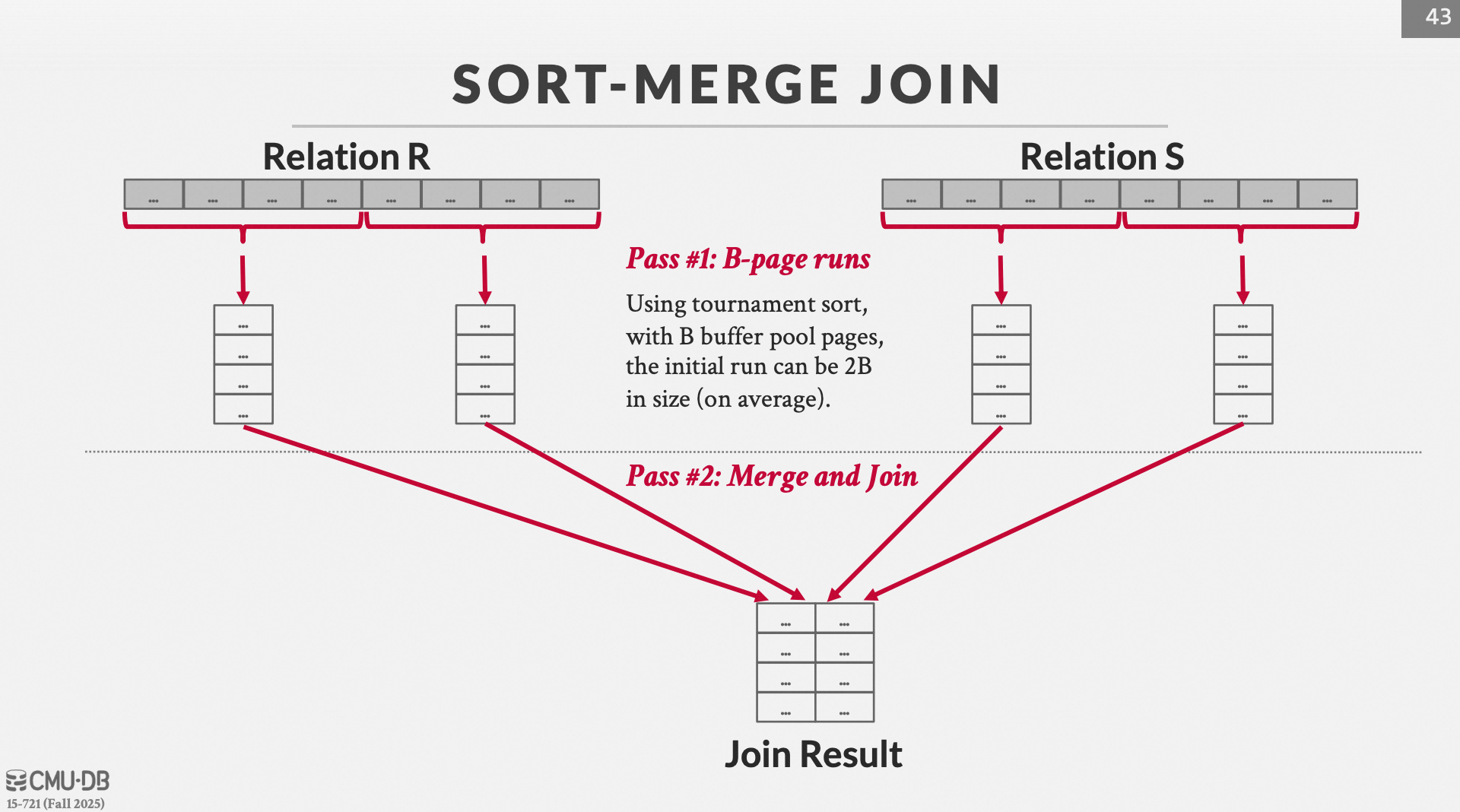
我们通过一个场景来了解这个算法的妙处：假设内存有B个pages，关系 R R R 和 S S S 要进行Sort-Merge Join。

1. 标准的"两阶段" Sort-Merge Join (非优化)

通常情况下，我们认为排序和连接是两个独立的步骤：

排序阶段 (Sort Phase)：
- 读取关系 R R R，生成许多排好序的小文件（Runs）。
- 将这些 Runs 归并成一个巨大的、排好序的 R R R 文件，写回磁盘。
- 对 S S S 执行同样操作，写回磁盘。
连接阶段 (Join Phase)：
- 从磁盘同时读取排好序的 R R R 和 S S S。
- 用双指针扫描，匹配并输出结果。

这种做法的缺点 ：在排序的最后一步，你把数据排好序写进磁盘，然后马上又把它读出来做 Join。这一写一读是多余的。

2. "一边归并一边 Join" (On-the-fly Join)

如果我们能跳过"写回排好序的大文件"这一步，直接在内存里完成最后的归并 ，并同时把结果交给 Join 逻辑，就能节省大量的 I/O。

条件是什么？

为了实现这一点，内存（ B B B 个页）必须能同时撑得住所有的初始归并段（Runs）。

假设 R R R 生成了 k _ R k\_R k_R 个 Runs。
假设 S S S 生成了 k _ S k\_S k_S 个 Runs。
在归并时，我们每一路 Run 都需要占据 1 个内存页 作为输入缓冲区。
如果我们想同时归并

k _ R + k _ S ≤ B − 1 k\_R + k\_S \le B - 1 k_R + k_S ≤ B − 1（留 1 页给输出结果）

假设我们已经用锦标赛排序在磁盘上生成了 R R R 的 10 个 Runs 和 S S S 的 10 个 Runs，而内存 B = 22 B=22 B=22。

内存分配：
- 分配 10 个页给 R R R 的 10 个 Runs（每个 Run 读入第一页）。
- 分配 10 个页给 S S S 的 10 个 Runs（每个 Run 读入第一页）。
- 还剩 2 个页做 Join 处理和输出缓冲。
执行逻辑：
- Merge 逻辑 ：从 R R R 的 10 个缓冲区里挑出最小的记录。
- Join 逻辑 ：拿到这个 R R R 的最小记录，去和从 S S S 的 10 个缓冲区里归并出来的最小记录做匹配。
- 如果某个缓冲区的页读完了，立刻从磁盘加载该 Run 的下一页。
结果：数据从磁盘的多个 Run 文件中读入内存，经过一次比较，直接输出 Join 结果。

为什么锦标赛排序（Tournament Sort）关键？

锦标赛排序生成的 Run 长度平均是 2 B 2B 2B。

R R R的 Runs 数量 k _ R ≈ N / 2 B k\_R \approx N / 2B k_R ≈ N / 2B。
S S S的 Runs 数量 k _ S ≈ M / 2 B k\_S \approx M / 2B k_S ≈ M / 2B。

如果没有锦标赛排序（使用普通的内存快排），Run 的长度只有 B B B，那么 Runs 的数量就会翻倍，变成 N / B N/B N/B 和 M / B M/B M/B。

公式对比：

使用锦标赛排序 ：只要 N + M 2 B ≤ B − 1 \frac{N+M}{2B} \le B-1 2BN+M ≤ B−1，就能一次性完成 Merge + Join。
不使用锦标赛排序 ：需要 N + M B ≤ B − 1 \frac{N+M}{B} \le B-1 BN+M ≤ B−1。

结论："On-the-fly Join" 节省了整整一轮对排序后数据的写和读（ 2 ( N + M ) 2(N+M) 2(N+M) 次 I/O ）。而锦标赛排序因为能产生更长、更少的初始 Run，使得我们在面对更大的数据集 （数据量最高可达约 2 B 2 2B^2 2B2）时，依然能满足内存约束，强行在两趟（Two-Pass）内完成整个 Join 过程。。

3. 核心机制：为什么锦标赛排序能生成更长的 Run？

在传统的外部排序中，我们通常将内存（ B B B 个页）填满，用快速排序排好序，写出一个大小为 B B B 的 Run。

而锦标赛排序（置换选择策略）的操作方式不同：

初始化 ：将内存 B B B 中能容纳的所有记录构建一个最小堆（锦标赛树）。
输出与填补：
- 从树顶输出当前最小值（设为 Last_Output）。
- 立即从输入端读取一条新记录填补空位。
冻结机制（关键）：
- 如果新读入的记录比 **Last_Output** 大，它仍有机会参与竞争并进入当前的 Run。
- 如果新读入的记录比 **Last_Output** 小，它无法进入当前 Run（否则会破坏有序性），将其"冻结"，留在树中但不参加比较，直到下一个 Run 开始。
循环：直到树中所有节点都被冻结，当前 Run 结束，开始新的 Run。

**结论：**随机分布情况下，新读入的记录被冻结的概率是50%，因此平均读入2B的记录才会使得树完全被冻结，开始下一个RUN，即平均初始RUN的长度是 2 B 2B 2B，是传统内存快排（长度为 B B B）的 2倍。

4. 算法局限性与实际考量

虽然锦标赛排序能减少 I/O，但在现代数据库（如 PostgreSQL, SQL Server）中，它并非总是首选，原因如下：

CPU 缓存不友好：锦标赛树（堆）在内存中的访问模式是跳跃的，而快速排序虽然 I/O Pass 可能多一点，但其内存访问是连续的，CPU 缓存命中率更高。
数据倾斜 ：如果输入数据是逆序的，锦标赛排序生成的 Run 长度退化为 B B B（和普通排序一样）；如果是基本有序的，长度则远超 2 B 2B 2B。
实现复杂性：管理"冻结"节点和动态堆结构比简单的快排复杂。

5. 总结

在内存 B B B 受限的情况下，使用锦标赛排序执行 Sort-Merge Join 的分析如下：

优势：初始 Run 长度翻倍（平均 2 B 2B 2B），初始 Run 数量减半。
I/O 收益 ：极大提高了在 2 趟（Passes）内完成排序的可能性。如果减少了一趟归并，总 I/O 减少约 2 ( M + N ) 2(M+N) 2(M+N) 次。
适用场景 ：当数据量极大（ B 2 B^2 B2 临界点）且磁盘 I/O 是主要瓶颈时，锦标赛排序是极佳的优化方案。

6. 延伸

这里的 B 2 B^2 B2 实际上是两趟排序（Two-Pass Sort）所能处理的上限阈值。

1. 什么是 "Two-Pass"（两趟）排序？

在外部排序中，I/O 开销最直接的衡量标准是 Pass（趟数）。

Pass 0：生成初始 Runs（归并段）。
Pass 1：将所有 Runs 归并成一个有序序列。

如果数据量太大，Pass 1 无法一次性处理完所有的 Runs，就需要 Pass 2, Pass 3... 。每多一趟，I/O 开销就增加 2 × ( M + N ) 2 \times (M+N) 2 × (M+N) 次。因此，数据库开发者总是想方设法把排序控制在 Two-Pass 之内。

2. 为什么临界点是 B 2 B^2 B2？

假设内存有 B B B 个页面：

使用普通排序（如快排）：

第一步（生成段） ：每个段的大小是 B B B。
段的数量 ：如果总数据量是 N N N，则产生 N / B N / B N / B 个段。
第二步（归并）：归并阶段，内存必须为每个段分配 1 个页面作为输入缓冲区。
约束条件 ：段的数量不能超过内存容量，即 N / B ≤ B − 1 N / B \le B - 1 N / B ≤ B − 1（约等于 B B B）。
结论：普通排序能通过 Two-Pass 处理的最大数据量 N ≈ B 2 N \approx \mathbf{B^2} N ≈ B2。

使用锦标赛排序（置换选择）：

第一步（生成段） ：每个段的大小平均是 2 B 2B 2B。
段的数量 ：总数据量 N N N，产生 N / 2 B N / 2B N / 2B 个段。
第二步（归并） ：同样的内存约束，段的数量 N / 2 B ≤ B − 1 N / 2B \le B - 1 N / 2B ≤ B − 1。
结论：锦标赛排序能通过 Two-Pass 处理的最大数据量 N ≈ 2 B 2 N \approx \mathbf{2B^2} N ≈ 2B2。

3. 为什么说在 B 2 B^2 B2 临界点时它是"极佳方案"？

这就是最巧妙的地方了。假设你的数据量 N N N 刚好比 B 2 B^2 B2 大一点点（例如 N = 1.5 B 2 N = 1.5 B^2 N = 1.5 B2）：

方案 A（普通排序） ：由于 N > B 2 N > B^2 N > B2，内存塞不下那么多 Runs 的缓冲区。你必须先归并一部分，写回磁盘，再归并第二次。 结果： 排序变成了 Three-Pass（三趟）。I/O 次数从 3 次扫描变成了 5 次扫描（读1写1，读2写2，读3）。
方案 B（锦标赛排序） ：由于它的上限是 2 B 2 2B^2 2B2，而 1.5 B 2 < 2 B 2 1.5 B^2 < 2B^2 1.5 B2 < 2B2，它依然能轻松地在 Two-Pass（两趟） 内完成。 结果： 只需要 3 次扫描。

性能差距：

在这种情况下，仅仅因为换了一个算法，I/O 开销直接减少了 40%（从 5 次扫描降到 3 次扫描）。

MySQL深度翻页优化技巧

既然我们刚才讨论了深奥的排序算法和 I/O 优化，我分享一个在 MySQL 实际开发中，利用"延迟关联"（Deferred Join）来大幅提升大分页查询性能的技巧。

这个技巧的本质，其实和你刚才学的"减少 I/O 成本"异曲同工。

场景：深度分页（Deep Paging）的性能陷阱

假设你有一个 500 万行的订单表 orders，你想看第 100,000 页的数据（每页 20 条）：

sql 复制代码

-- 这种查询在数据量大时会非常慢
SELECT * FROM orders 
ORDER BY create_time 
LIMIT 1000000, 20;

为什么慢？（结合我们刚才聊的 I/O 理论）

无效 I/O 极高 ：MySQL 会根据索引找到这 1,000,020 条记录，由于是 SELECT *，它必须执行回表操作，把这 100 万行完整的数据页从磁盘加载到内存。
内存浪费：即使它最后只需要那 20 条，但它之前扫描的 100 万条记录也都经历了"读取-排序-舍弃"的过程。这造成了海量的磁盘 I/O。

高阶技巧：延迟关联（Deferred Join）

我们可以利用 **覆盖索引（Covering Index）**先只取 ID，再把需要的 20 条数据关联回来：

sql 复制代码

-- 优化后的写法
SELECT o.* 
FROM orders o
JOIN (
    -- 这一步只走索引，不回表，极其轻量
    SELECT id FROM orders 
    ORDER BY create_time 
    LIMIT 1000000, 20
) AS tmp ON o.id = tmp.id;

为什么这个技巧有效？

子查询阶段（只读索引） ：SELECT id FROM orders ORDER BY create_time 只需要读取 create_time 和 id 两个字段。这两个字段通常都在同一个二级索引树上。MySQL 不需要访问完整的数据行（不需要回表），I/O 开销极小。
精准回表：子查询利用索引飞速跳过前 100 万行，最终只选出 20 个 ID。
主查询阶段 ：外层的 JOIN 只需要根据这 20 个 ID 去磁盘查 20 次，而不是 1,000,020 次。

终极优化：PolarDB MySQL Limit Offset Pushdown

官方文档

要理解为什么 PolarDB 的这种做法能大幅提升性能，我们需要对比 社区版 MySQL（原版） 和 优化版（如 PolarDB） 在处理 LIMIT Offset, N 时，内部执行路径的本质区别。

1. 社区版 MySQL 的痛点：SQL 层与引擎层的"沟通障碍"

在 MySQL 的架构中，分为 SQL 层（Server 层） 和 存储引擎层（InnoDB）。

执行流程（社区版）：

当执行 SELECT * FROM orders ORDER BY create_time LIMIT 1000000, 20 时：

引擎层（InnoDB） ：通过 idx_create_time 索引定位到数据。
强制回表 ：因为引擎层不知道 SQL 层到底要哪些行，它只知道 SQL 层请求了 SELECT *。所以，InnoDB 对每一条经过索引的记录，都会立刻根据 ID 回到主键索引（聚集索引）去查整行数据。
数据传输：InnoDB 将这一整行数据（包含 address, remark 等大字段）通过内存拷贝交给 SQL 层。
SQL 层丢弃：SQL 层接收到数据后，看了一下自己的计数器："哦，这是第 1 个，还没到 100 万，扔掉。"......"这是第 999,999 个，扔掉。"
达到 Offset：直到第 1,000,001 条，SQL 层才开始把数据放入结果集。

代价： 100 万次不必要的回表 + 100 万次无用的引擎与 SQL 层之间的大数据量传输。

2. PolarDB 的优化：Limit 下推（Limit Pushdown）

PolarDB修改了这一逻辑，让存储引擎变得"聪明"了。

执行流程（PolarDB）：

语义下推：SQL 层在调用引擎接口时，直接告诉 InnoDB："我要按这个索引排，但我前 100 万条都不要，你直接给我跳过，只要后面的 20 条。"
引擎层自过滤（关键）：
- InnoDB 扫描二级索引 idx_create_time。
- 对于前 100 万条数据，InnoDB 发现它们处于 OFFSET 范围内，由于它知道这些数据最终会被丢弃，所以它直接在索引层进行计数跳过，根本不去回表。
- 不回表 意味着没有随机 I/O，不传输意味着没有内存拷贝开销。
精准回表：只有当计数器超过 1,000,000 时，InnoDB 才会对后续的 20 条数据执行回表，并交给 SQL 层。

3. 一个形象的比喻

为了理解这个区别，我们想象你在餐厅点餐：

社区版 MySQL（愚蠢的传菜员） ：你告诉传菜员："我要看第 100 到 105 个菜的详情。" 传菜员跑到厨房，每看到一个菜，都把它装盘、装饰好、端到你面前。你扫一眼说："这是第 1 个，不要，端走。"......"这是第 99 个，不要，端走。" 这就导致厨师累死（回表），传菜员累死（传输），你也等得不耐烦（耗时）。
PolarDB（聪明的传菜员） ：你告诉传菜员："我要看第 100 到 105 个菜的详情。" 传菜员告诉厨师："前 99 个你别装盘了，数过去就行，从第 100 个开始准备。" 厨师在前 99 个菜时只是数数，不浪费盘子和精力。最后只端 5 盘菜给你。

4. 这种优化与"延迟关联"的关系

你可能会发现，这和我们之前写的 延迟关联（Deferred Join） 效果惊人地相似。

延迟关联 ：是程序员手动写的 SQL 技巧。通过子查询迫使 MySQL "先只看索引，后回表"。这是一种"在现有系统限制下"的曲线救国方案。
Limit 下推 ：是数据库内核层面 的自动优化。它让普通的 SELECT * 也能享受到延迟关联的性能，甚至更强（因为减少了子查询的开销）。

总结

PolarDB 的优化之所以强，是因为它从物理执行层面消灭了深翻页中最重的两部分负担：

消灭了 Offset 部分的回表 I/O（这占了 99% 的耗时）。
消灭了 SQL 层与引擎层之间的大规模数据拷贝。

性能对比

优化方法	平均3次执行时间
原始SQL	2.02 Sec
Deferred Join	0.14 Sec
Limit Pushdown	0.04 Sec

论文《ByteSlice: Pushing the Envelop of Main Memory Data Processing with a New Storage Layout》

这篇论文发表在数据库顶级会议 SIGMOD 2015 上。它的核心目标是：为了充分压榨现代 CPU 的计算能力（特别是 SIMD 指令集），设计一种全新的内存数据布局。

你可以把它看作是在内存数据库领域，对"如何存储数据"的一次降维打击式优化。

以下是该论文的核心思想和技术要点：

1. 核心背景：内存墙与 SIMD

在内存数据库中，数据读取已经很快了，瓶颈往往在于 CPU 的处理速度 。为了加速，现代数据库广泛使用 SIMD（单指令多数据流），即一个指令同时处理 8 个或 16 个整数。

但是，传统的存储方式对 SIMD 并不友好：

水平布局（Row-store）：不适合 SIMD。
列式布局（Column-store） ：虽然比行存好，但在处理非定长数据或**位压缩数据（Bit-packing）**时，CPU 需要花费大量精力去进行解压、移位和对齐，浪费了大量时钟周期。

2. ByteSlice 的存储设计

ByteSlice 提出了一种"字节切片 "的布局方式。它既不是单纯的行存，也不是单纯的列存，而是一种列内按字节拆分的布局。

假设我们有一组 32 位（4 字节）的整数列：

传统列存 ：连续存储 a V _ 1 , V _ 2 , V _ 3 ... V\_1, V\_2, V\_3 \dots V_1, V_2, V_3 ... 每个占 4 字节。
ByteSlice 存储：
- 它把所有整数的 第 1 个字节 （最高位字节）抽出来，连续排在一起，形成 Slice 0。
- 把所有整数的 第 2 个字节 抽出来，形成 Slice 1。
- 以此类推，形成 4 个 Slice。

为什么要这么做？ 因为 CPU 处理字节（Byte）的速度远远快于处理不规则的位（Bit）。

3. 三大核心优势

(1) 极致的 SIMD 优化

由于每个 Slice 里的数据都是字节对齐的，这完美契合了现代 CPU 的 SIMD 寄存器（如 SSE, AVX）。

在执行扫描（Scan）或过滤（Filter）时，CPU 可以一次性加载 16 个字节（16 个数据的最高位字节）进入寄存器，进行一次简单的比较指令。这比处理位压缩数据（Bit-packing）要快得多，因为不需要复杂的移位操作。

(2) 谓词下推与"提早退出"（Early Pruning）

这是 ByteSlice 最聪明的地方。在进行比较（如 WHERE column > 1000）时：

算法先扫描 Slice 0（最高位字节）。
如果某个数据的最高位字节已经能决定它大于或小于目标值，那么 这个数据的后续 3 个字节就永远不需要再从内存读入 CPU 了。
这极大地减少了内存带宽的压力，实现了类似于"剪枝"的效果。

(3) 优于位交织（Bit-weaving）

在 ByteSlice 之前，学术界有另一种技术叫 Bit-weaving（位交织）。Bit-weaving 是在位级别做切片。

ByteSlice 论文指出：位级别的操作在 CPU 上非常低效，因为 CPU 的基本处理单位是字节。ByteSlice 通过放弃细粒度的"位"而选择"字节"，在压缩率和处理性能之间找到了完美的平衡点。

4. 论文的贡献总结

新型布局：设计了 ByteSlice 这种高度对齐、适合 SIMD 的内存布局。
高效扫描算法：提出了一套基于比特掩码（Bitmask）的扫描算法，能够利用 SIMD 指令快速合并多个字节切片的比较结果。
性能飞跃 ：实验显示，ByteSlice 在执行范围查询和过滤时，性能比当时最先进的列存技术（如 Bit-weaving 或采用 Snappy 压缩的列存）快了 6 到 10 倍。

5. 与之前问题的关联

你会发现，ByteSlice 的思想 "Limit 下推" 或者 "延迟关联" 有一种异曲同工之妙：

延迟关联 是在 SQL 逻辑层面尽量少读行。
Limit 下推 是在引擎层面尽量少回表。
ByteSlice 则是在硬件底层层面，尽量少读字节（Byte）。

它们都在贯彻同一个数据库设计的最高哲学：最快的操作，就是那些你根本不需要做的操作。