C4.5 决策树
C4.5 是 Ross Quinlan 在 1993 年提出的,作为 ID3 算法的改进版本。相当于对信息增益进行修正,增加一个惩罚系数。
ID3树的不足:偏向于选择种类多的特征作为分裂依据。(sklearn没有直接内置)
信息增益率
• 信息增益率 = 信息增益 /特征熵 (特征的信息种类多,信息增益大G(D,a),特征熵大IV)
• 计算方法

例:
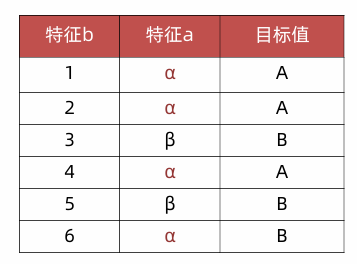
需求:求特征a、b的信息增益率。
• 特征a的信息增益率:
1 信息增益 :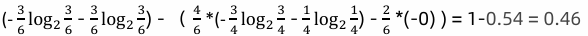
2 IV信息熵: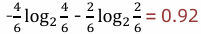
3 信息增益率:信息增益/信息熵=0.46/0.92=0.5
• 特征b的信息增益率:
1 信息增益: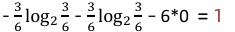
2 IV信息熵: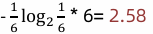
3 信息增益率:信息增益/信息熵=1/2.58=0.39
• 结论:特征a的信息增益率大于特征b的信息增益率,根据信息增益率,应该选择特征a作为分裂特征。
CART决策树
Cart模型是一种决策树模型,它即可以用于分类,也可以用于回归。
Cart回归树使用平方误差最小化策略, Cart分类生成树采用的基尼指数最小化策略。
公式:

基尼值Gini(D):从数据集D中随机抽取两个样本,其类别标记不一致的概率。 Gini(D)值越小,数据集D的纯度越高。
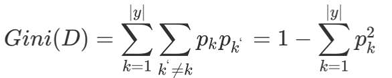
基尼指数Gini_index(D):选择使划分后基尼系数最小的属性作为最优化分属性。
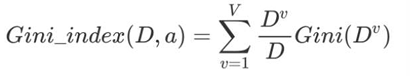
注意:
1.信息增益(ID3)、信息增益率值越大(C4.5),则说明优先选择该特征。
2.基尼指数值越小(CART),则说明优先选择该特征。
例
• 已知:是否拖欠贷款数据。
• 需求:计算各特征的基尼指数,选择最优分裂点
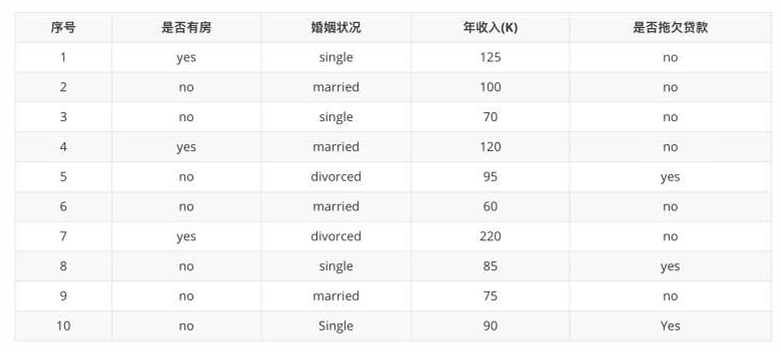
是否有房
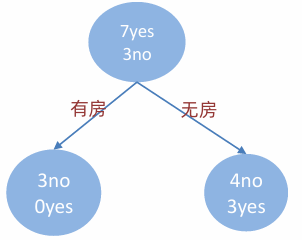
有房子的基尼值: 有房子有 1、4、7 共计三个样本,对应:3个no、0个yes
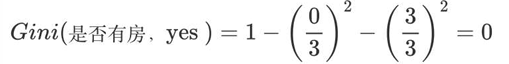
无房子的基尼值:无房子有 2、3、5、6、8、9、10 共七个样本,对应:4个no、3个yes
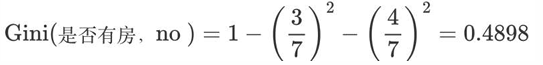
基尼系数:第一部分样本占了总样本的 3/10、第二部分样本占了总样本的 7/10
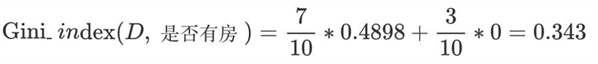
婚姻状况
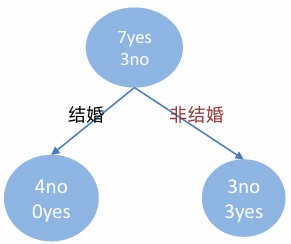
1 计算 {married} 和 {single,divorced} 情况下的基尼指数
• 结婚的基尼值,有 2、4、6、9 共 4 个样本,并且对应目标值全部为 no: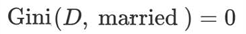
• 不结婚的基尼值,有 1、3、5、7、8、10 共 6 个样本,并且对应 3 个 no,3 个 yes
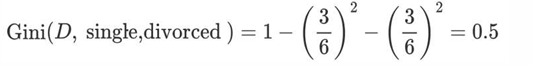
• 以 married 作为分裂点的基尼指数:
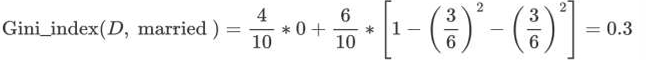
2 计算 {single} | {married,divorced} 情况下基尼指数(单身4,结婚和离婚6, 一个离婚有拖欠)
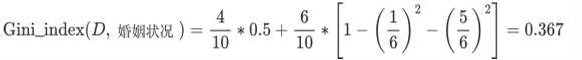
3 计算 {divorced} | {single,married} 情况下基尼指数(离婚2,结婚和单身8, 两个单身有拖欠)
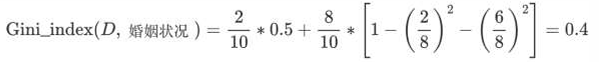
最终:该特征的基尼值为 0.3,并且预选分裂点为:{married} 和 {single,divorced}
年收入
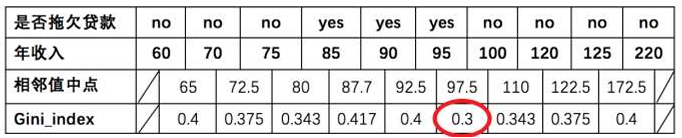
1 先将数值型属性升序排列,以相邻中间值作为待确定分裂点:

2.计算:
分割点 65
左:60 (no) → N_left=1, yes=0, no=1 → Gini_left = 1 - (0² + 1²) = 0
右:70~220 (6 no + 3 yes) → N_right=9, yes=3, no=6 → Gini_right = 1 - (3/9)² - (6/9)² = 1 - 0.111 - 0.444 = 0.445
加权 Gini = (1/10)*0 + (9/10)*0.445 = 0.4005
分割点 72.5
左:60,70 (2 no) → Gini_left = 0
右:75~220 (5 no + 3 yes) → N_right=8, yes=3, no=5 → Gini_right = 1 - (3/8)² - (5/8)² = 1 - 0.1406 - 0.3906 = 0.4688
加权 Gini = (2/10)*0 + (8/10)*0.4688 = 0.3750
分割点 80
左:60,70,75 (3 no) → Gini_left = 0
右:85~220 (4 no + 3 yes) → N_right=7, yes=3, no=4 → Gini_right = 1 - (3/7)² - (4/7)² = 1 - 0.1837 - 0.3265 = 0.4898
加权 Gini = (3/10)*0 + (7/10)*0.4898 = 0.3429
,,,,,
3 以此类推计算所有分割点的基尼指数,最小的基尼指数为 0.3
第1轮结果
以是否有房作为分裂点的基尼指数为:0.343
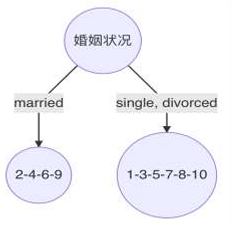
以婚姻状况为分裂特征、以 married 作为分裂点的基尼指数为:0.3
以年收入作为分裂特征、以 97.5 作为分裂点的的基尼指数为:0.3
第2轮
1 样本 2、4、6、9 样本的类别都是 no,已经达到最大纯度 所以,该节点不需要再继续分裂。
2 样本 1、3、5、7、8、10 样本中仍然包含 4 个 no,2 个 yes 该节点并未达到要求的纯度,需要继续划分。
3 右子树的数据集变为: 1、3、5、7、8、10,在该数据集中计算 不同特征的基尼指数,选择基尼指数最小的特征继续分裂。
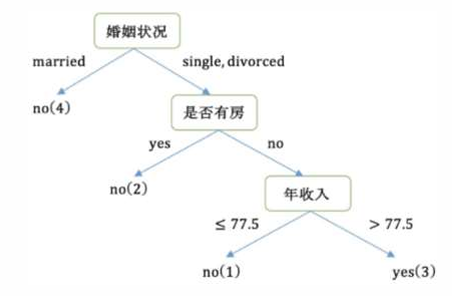
重复上述过程,直到构建完成整个决策树。
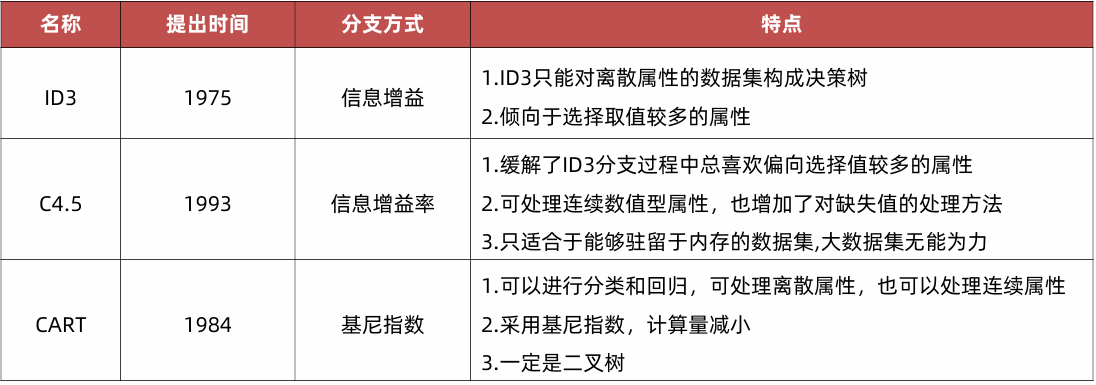
三种分类树的对比
代码
python
# 1.导入依赖包
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
from sklearn.tree import export_graphviz
import graphviz
def dm01():
# 2.读数据到内存并预处理
# 2.1 读取数据
taitan_df = pd.read_csv("./train.csv")
print(taitan_df.head(2)) # 查看前2条数据
print(taitan_df.info) # 查看特性信息
# 2.2 数据处理,确定x y
x = taitan_df[['Pclass', 'Age', 'Sex']].copy()
y = taitan_df['Survived'].copy()
# 2.3缺失值处理
x['Age'].fillna(x['Age'].mean(), inplace=True)
print('x -->1', x.head(10))
# 2.4 pclass类别型数据,需要转数值one-hot编码
x = pd.get_dummies(x)
print('x -->2', x.head(10))
# 2.5 数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.20, random_state=33)
# 3.训练模型,实例化决策树模型
estimator = DecisionTreeClassifier()
estimator.fit(x_train, y_train)
# 4.模型预测
y_pred = estimator.predict(x_test)
# 5.模型评估
# 5.1 输出预测准确率
myret = estimator.score(x_test, y_test)
print('myret-->\n', myret)
# 5.2 更加详细的分类性能
myreport = classification_report(y_pred, y_test, target_names=['died', 'survived'])
print('myreport-->\n', myreport)
# 5.3 决策树可视化
plt.figure(figsize=(50, 25)) # 设置图形大小
plot_tree(
estimator,
max_depth=10,
filled=True,
feature_names=['Pclass', 'Age', 'Sex_female', 'Sex_male'],
class_names=['died', 'survived'],
fontsize=8, # 增加字体大小
rounded=True, # 添加圆角,使图形更美观
)
plt.tight_layout()
plt.savefig('tree_full.png', dpi=300, bbox_inches='tight')
# plt.show()
dm01()执行结果
python
PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket Fare Cabin Embarked
0 1 0 3 Braund, Mr. Owen Harris male 22.0 1 0 A/5 21171 7.2500 NaN S
1 2 1 1 Cumings, Mrs. John Bradley (Florence Briggs Th... female 38.0 1 0 PC 17599 71.2833 C85 C
<bound method DataFrame.info of PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket Fare Cabin Embarked
0 1 0 3 Braund, Mr. Owen Harris male 22.0 1 0 A/5 21171 7.2500 NaN S
1 2 1 1 Cumings, Mrs. John Bradley (Florence Briggs Th... female 38.0 1 0 PC 17599 71.2833 C85 C
2 3 1 3 Heikkinen, Miss. Laina female 26.0 0 0 STON/O2. 3101282 7.9250 NaN S
3 4 1 1 Futrelle, Mrs. Jacques Heath (Lily May Peel) female 35.0 1 0 113803 53.1000 C123 S
4 5 0 3 Allen, Mr. William Henry male 35.0 0 0 373450 8.0500 NaN S
.. ... ... ... ... ... ... ... ... ... ... ... ...
886 887 0 2 Montvila, Rev. Juozas male 27.0 0 0 211536 13.0000 NaN S
887 888 1 1 Graham, Miss. Margaret Edith female 19.0 0 0 112053 30.0000 B42 S
888 889 0 3 Johnston, Miss. Catherine Helen "Carrie" female NaN 1 2 W./C. 6607 23.4500 NaN S
889 890 1 1 Behr, Mr. Karl Howell male 26.0 0 0 111369 30.0000 C148 C
890 891 0 3 Dooley, Mr. Patrick male 32.0 0 0 370376 7.7500 NaN Q
[891 rows x 12 columns]>
x -->1 Pclass Age Sex
0 3 22.000000 male
1 1 38.000000 female
2 3 26.000000 female
3 1 35.000000 female
4 3 35.000000 male
5 3 29.699118 male
6 1 54.000000 male
7 3 2.000000 male
8 3 27.000000 female
9 2 14.000000 female
x -->2 Pclass Age Sex_female Sex_male
0 3 22.000000 False True
1 1 38.000000 True False
2 3 26.000000 True False
3 1 35.000000 True False
4 3 35.000000 False True
5 3 29.699118 False True
6 1 54.000000 False True
7 3 2.000000 False True
8 3 27.000000 True False
9 2 14.000000 True False
myret-->
0.8491620111731844
myreport-->
precision recall f1-score support
died 0.93 0.84 0.88 118
survived 0.74 0.87 0.80 61
accuracy 0.85 179
macro avg 0.83 0.85 0.84 179
weighted avg 0.86 0.85 0.85 179