
本题求自增子序列,是不能对原数组进行排序的,排完序的数组都是自增子序列了。
所以不能使用之前几道题的去重逻辑!
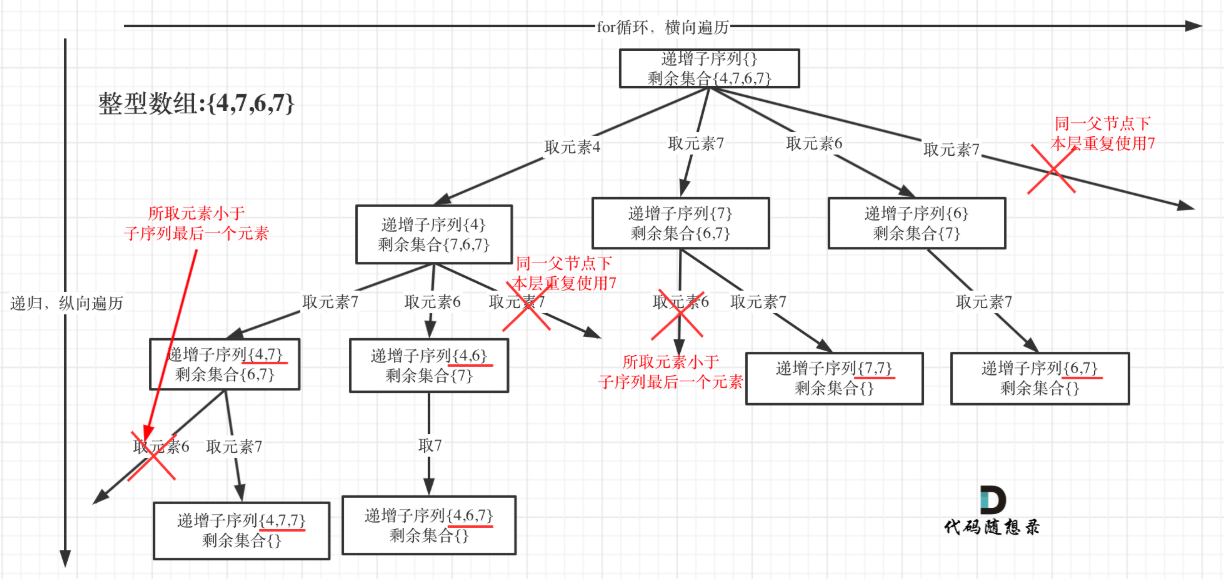
用[4, 7, 6, 7]这个数组来举例,抽象为树形结构如图:
cpp
class Solution {
private:
// 存储所有递增子序列的结果
vector<vector<int>> result;
// 存储当前递归路径上的递增子序列
vector<int> path;
// 回溯函数,寻找递增子序列
// nums: 输入数组
// startIndex: 当前递归开始搜索的索引位置
void backtracking(vector<int>& nums, int startIndex) {
// 如果当前路径长度大于1(至少两个元素),说明找到了一个有效子序列
if (path.size() > 1) {
// 将当前路径添加到结果集中
result.push_back(path);
// 注意:这里不能加return,因为即使找到了一个子序列,还可以继续添加更多元素
// 形成更长的递增子序列
}
// 使用unordered_set对本层(当前递归深度)的元素进行去重
// 避免在同一递归层级选择相同的数字,防止重复子序列
unordered_set<int> uset;
if(startIndex == nums.size()) return; / /这一行代码用来做终止条件
// 其实可以不需要加终止条件,因为startIndex >= nums.size(),本层for循环本来也结束了。
// 从startIndex开始遍历数组
for (int i = startIndex; i < nums.size(); i++) {
// 条件判断:如果以下两个条件之一满足,则跳过当前数字
// 1. 当前路径非空且当前数字小于路径最后一个数字(不是递增)
// 2. 当前数字已经在本层中使用过(去重)
if ((!path.empty() && nums[i] < path.back())
|| uset.find(nums[i]) != uset.end()) {
continue; // 跳过当前数字,继续下一轮循环
}
// 记录当前数字在本层中已使用,本层后面不能再使用相同的数字
uset.insert(nums[i]);
// 选择当前数字,加入路径
path.push_back(nums[i]);
// 递归调用,从下一个位置继续搜索
// i+1保证每个数字在子序列中最多使用一次(因为子序列要保序)
backtracking(nums, i + 1);
// 回溯:撤销选择,移除最后加入的数字
// 尝试其他可能性
path.pop_back();
// 注意:uset不需要回溯,因为它是局部变量,只在当前递归层有效
// 每次递归调用都会创建新的uset
}
}
public:
// 主函数:寻找所有递增子序列
vector<vector<int>> findSubsequences(vector<int>& nums) {
// 清空结果集和路径(确保多次调用时状态正确)
result.clear();
path.clear();
// 从索引0开始回溯搜索
backtracking(nums, 0);
// 返回所有找到的递增子序列
return result;
}
};为什么不能用 vector<int> uset; 来替代 unordered_set<int> uset?
**(1) 使用 unordered_set 查找:平均 O(1) 时间复杂度
(2) 使用 vector 查找:需要遍历,O(n) 时间复杂度**
在这个算法中,我们需要 快速判断当前元素是否在本层已经使用过:
-
unordered_set:哈希表,专门用于快速查找和去重 -
vector:顺序容器,没有内置的去重机制
cpp
unordered_set<int> uset;
for (int i = startIndex; i < nums.size(); i++) {
// 查找:O(1) 平均时间复杂度
if (uset.find(nums[i]) != uset.end()) {
continue;
}
uset.insert(nums[i]); // 插入:O(1)
}
cpp
vector<int> uset;
for (int i = startIndex; i < nums.size(); i++) {
// 每次都需要遍历整个 vector 来检查是否已存在
bool exists = false;
for (int num : uset) { // O(n) 查找
if (num == nums[i]) {
exists = true;
break;
}
}
if (exists) continue;
uset.push_back(nums[i]); // 插入:O(1)
}虽然 unordered_set 比 vector 使用更多内存(哈希表的开销),但:
-
每一层的
uset在函数返回时都会被销毁 -
查找的时间复杂度优势对于回溯算法更重要
cpp
uset.find(nums[i]) != uset.end()1. uset.find(nums[i])
-
find()是unordered_set的成员函数 -
在集合中查找值为
nums[i]的元素 -
返回值:一个迭代器(iterator)
-
如果找到元素:返回指向该元素的迭代器
-
如果没找到:返回
uset.end()迭代器
-
2. uset.end()
-
end()是容器的成员函数 -
返回指向容器"末尾之后"的迭代器(不是最后一个元素,而是最后一个元素的下一个位置)
-
用作"未找到"的标记值
3. != 比较运算符
-
比较两个迭代器是否指向同一位置
-
如果
find()返回的迭代器 不等于end(),说明找到了元素 -
如果 等于
end(),说明没找到
以 数组 [4, 7, 6, 7] 为例,详细分析代码每一步的执行过程
初始状态
nums = [4, 7, 6, 7] result = [] path = []
第一步:findSubsequences(nums) 主函数
result.clear(); // result = [] path.clear(); // path = [] backtracking(nums, 0);
第二步:调用 backtracking(nums, 0)
cppvoid backtracking(vector<int>& nums, int startIndex) { // 如果当前路径长度大于1(至少两个元素),说明找到了一个有效子序列 if (path.size() > 1) { // 将当前路径添加到结果集中 result.push_back(path); // 注意:这里不能加return,因为即使找到了一个子序列,还可以继续添加更多元素 // 形成更长的递增子序列 } // 使用unordered_set对本层(当前递归深度)的元素进行去重 // 避免在同一递归层级选择相同的数字,防止重复子序列 unordered_set<int> uset;
传入的参数:startIndex = 0 if条件判断不满足 创建 uset = {} (空集合)
cppfor (int i = startIndex; i < nums.size(); i++) { // 条件判断:如果以下两个条件之一满足,则跳过当前数字 // 1. 当前路径非空且当前数字小于路径最后一个数字(不是递增) // 2. 当前数字已经在本层中使用过(去重) if ((!path.empty() && nums[i] < path.back()) || uset.find(nums[i]) != uset.end()) { continue; // 跳过当前数字,继续下一轮循环 } // 记录当前数字在本层中已使用,本层后面不能再使用相同的数字 uset.insert(nums[i]); // 选择当前数字,加入路径 path.push_back(nums[i]); // 递归调用,从下一个位置继续搜索 // i+1保证每个数字在子序列中最多使用一次(因为子序列要保序) backtracking(nums, i + 1); // 回溯:撤销选择,移除最后加入的数字 // 尝试其他可能性 path.pop_back(); // 注意:uset不需要回溯,因为它是局部变量,只在当前递归层有效 // 每次递归调用都会创建新的uset }
for循环,i = 0,nums[0] = 4 if条件判断不满足 uset.insert(4); // uset = {4} path.push_back(4); // path = [4] backtracking(nums, 1);
第三步:调用 backtracking(nums, 1)
传入的参数:startIndex = 1 建新的 uset = {} (局部变量) for循环(i从1到3)i = 1,nums[1] = 7 if条件判断: // !path.empty() = true // nums[1] = 7,path.back() = 4,7 >= 4 满足递增条件true // uset.find(7) = end(),说明7还不在集合中 false uset.insert(7); // uset = {7} path.push_back(7); // path = [4, 7] backtracking(nums, 2);
第四步:调用 backtracking(nums, 2)
传入的参数:startIndex = 2 path.size() = 2 > 1,添加结果: result.push_back([4, 7]); // result = [[4, 7]] 创建新的 uset = {} for循环(i从2到3)i = 2, nums[2] = 6 if条件判断: // !path.empty() = true // nums[2] = 6,path.back() = 7,6 < 7 不满足递增! nums[i] < path.back() 为true 条件成立,执行 if语句continue i++ -> i=3 ,nums[3] = 7 if条件判断: // !path.empty() = true // nums[3] = 7,path.back() = 7,7 >= 7 递增 , 所以为false !path.empty() && nums[i] < path.back() 为 false // uset.find(7) = end(),不在集合中 // 两个条件都不成立,不执行if语句,继续执行下一行代码 uset.insert(7); // uset = {7} path.push_back(7); // path = [4, 7, 7] backtracking(nums, 4);
第五步:调用 backtracking(nums, 4)
传入的参数:startIndex = 4 if判断:path.size() = 3 > 1,添加结果: result.push_back([4, 7, 7]); // result = [[4, 7], [4, 7, 7]] 创建新的 uset = {} for 循环条件:i = 4 < 4 不成立,直接结束本次调用
第六步:回到调用 backtracking(nums, 2) 的剩余部分
path.pop_back(); // path = [4, 7] // i 循环结束(已经到3,下一个是4,超过数组长度)
第七步:回到调用 backtracking(nums, 1) 的剩余部分
path.pop_back(); // path = [4] // 继续循环:i = 2,nums[2] = 6 for循环, i=2 if条件判断: // !path.empty() = true // nums[2] = 6,path.back() = 4,6 >= 4 递增 false // uset.find(6) = end(),不在集合中(注意:这是第二次调用的uset,当前是{7}) // 两个条件都不成立,继续执行 uset.insert(6); // uset = {7, 6} path.push_back(6); // path = [4, 6] backtracking(nums, 3);
.........
.........
.........