【算法基础篇】（五十一）组合数学入门：核心概念 + 4 种求组合数方法，带你快速熟悉组合问题！

前言

在编程世界里，组合数学是一门绕不开的 "内功心法"。无论是算法竞赛中的排列组合问题、动态规划中的状态计数，还是实际开发中的概率统计场景，都离不开组合数学的支撑。而组合数学的核心，莫过于对计数原理、排列组合、二项式定理这些基础概念的深刻理解，以及灵活运用各种方法求解组合数。

本文将从最基础的概念入手，由浅入深地拆解组合数学的核心知识点，再聚焦 "求组合数" 这一高频考点，详细讲解 4 种不同场景下的最优解法。无论你是算法新手，还是准备冲击竞赛的进阶选手，相信都能从本文中有所收获。下面就让我们正式开始吧！

一、组合数学核心概念拆解

1.1 计数原理：加法与乘法，组合数学的基石

计数原理是组合数学的入门知识，看似简单，却是所有复杂计数问题的基础。它包含两个核心：加法原理和乘法原理。

加法原理：分类相加，择一即可

定义：如果完成一个事件有 n 类独立的方法，第 i 类方法有 a_i 种具体实现，那么完成这个事件的总方法数就是所有类别方法数的和，即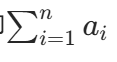（也就是 a₁+a₂+...+aₙ）。

通俗理解：就像去餐厅吃饭，主食有米饭、面条、馒头 3 种选择，任选一种就能解决主食问题，总选择数就是 3 种，这就是加法原理的直观体现 ------"分类选择，选一个就够"。

乘法原理：分步相乘，缺一不可

定义：如果完成一个事件需要 n 个连续的步骤，第 i 个步骤有 a_i 种实现方式，那么完成这个事件的总方法数就是所有步骤方法数的乘积，即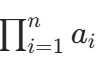（也就是 a₁×a₂×...×aₙ）。

通俗理解：还是吃饭的例子，要是不仅选主食，还要选菜。主食有 3 种，菜有 4 种，那么一顿饭的搭配方案就是 3×4=12 种 ------ 因为先选主食（3 种选择），再选菜（4 种选择），两个步骤必须都完成，才能构成一顿完整的饭，这就是 "分步执行，缺一不可"。

经典示例验证

题目：书架上有不同的数学书 3 本，不同的物理书 4 本，不同的化学书 5 本。

问题 1：从中任取一本，有多少种不同的取法？解答：取一本书属于 "分类选择"，数学书、物理书、化学书是三类独立的选择，用加法原理：3+4+5=12 种。

问题 2：从中每种各取一本，有多少种不同的取法？解答：每种各取一本需要分三步 ------ 先取数学书（3 种），再取物理书（4 种），最后取化学书（5 种），用乘法原理：3×4×5=60 种。

这两个问题清晰地展示了加法原理和乘法原理的区别：加法原理对应 "分类"，乘法原理对应 "分步"。

1.2 排列组合：有序与无序，核心计数模型

排列组合是组合数学的核心，主要研究 "从 n 个不同元素中选取 m 个元素" 的计数问题，关键区别在于 "选取的元素是否有序"。

排列数：有序选取，顺序不同算不同

定义：从 n 个不同的元素中，任取 m 个元素（m≤n）排成一列，所有可能的取法个数称为排列数，记作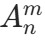（也常用 P (n,m) 表示）。

计算公式：

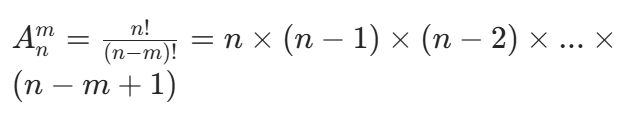
（注：n! 表示 n 的阶乘，即 n×(n-1)×...×1；0! 规定为 1）

理解：排列强调 "顺序"。比如从 1、2、3、4 四个数中选 3 个排成一列，123 和 321 是不同的排列，因为顺序不同。计算时，第一个位置有 n 种选择，第二个位置有 n-1 种（选了一个元素后剩下的），以此类推，直到选够 m 个位置，所以是 m 个连续整数的乘积。

示例：计算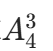

按照公式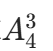：=(4−3)! / 4!=4×3×2×1 / 1=4×3×2=24种，和直观枚举的结果一致。

组合数：无序选取，顺序不同算相同

定义：从 n 个不同的元素中，任取 m 个元素（m≤n）组成一组（不考虑顺序），所有可能的取法个数称为组合数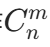，记作（也记作）。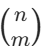

计算公式：

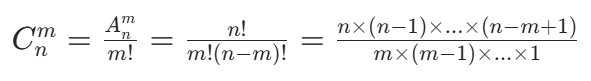
理解：组合不考虑顺序，只关注 "选了哪些元素"。比如从 1、2、3、4 中选 3 个元素，{1,2,3} 和 {3,2,1} 是同一个组合。因此，组合数是排列数除以 m!（m 个元素的全排列数，即消除顺序带来的重复计数）。

核心性质 ：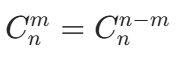

这个性质非常实用，比如计算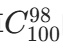时，直接用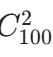计算更简单（因为 100-98=2），大大减少计算量。

特殊情况说明

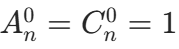：从 n 个元素中选 0 个元素，只有 "不选" 这一种方式。
0! = 1：阶乘的特殊规定，是公式推导的基础。
当 m > n 时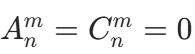，：从 n 个元素中选比 n 多的元素，显然不可能，所以方法数为 0。

1.3 二项式定理与杨辉三角：组合数的另一种存在形式

二项式定理揭示了 (a+b)ⁿ展开式的系数与组合数的关系，而杨辉三角则是二项式系数的直观表现形式。

二项式定理

公式：

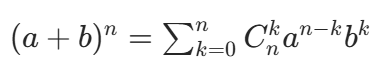
其中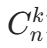，就是二项式展开式中第 k+1 项的系数（称为二项式系数）。

示例：展开 (a+b)³

根据定理：

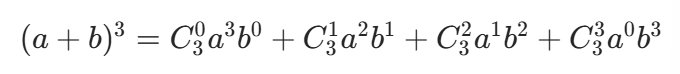
代入组合数计算：= 1×a³×1 + 3×a²×b + 3×a×b² + 1×1×b³= a³ + 3a²b + 3ab² + b³

杨辉三角：二项式系数的可视化

杨辉三角是一个由数字组成的三角形，它的第 i 行（从 0 开始计数）恰好是 (a+b)ⁱ展开式的二项式系数。

杨辉三角的结构：

第 0 行：1
第 1 行：1 1
第 2 行：1 2 1
第 3 行：1 3 3 1
第 4 行：1 4 6 4 1
...

核心规律：

每行的首尾元素都是 1。

中间的每个元素等于它上方两个元素的和，即。这个规律是后续用杨辉三角求组合数的理论基础。

杨辉三角的实用价值在于 "打表"------ 可以提前预处理出一定范围内的所有二项式系数（即组合数），后续查询时直接取用，效率极高。

二、求组合数的 4 种方法：场景适配 + C++ 实现

组合数的计算是算法题中的高频考点，但不同题目的数据范围差异很大，因此需要根据 n、m 的大小、查询次数等条件选择合适的方法。以下是 4 种最常用的求组合数方法，涵盖了从简单到复杂的各类场景。

方法一：循环直接计算（单次查询，n≤1e6）

适用场景

单次查询组合数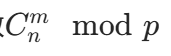（p 为质数且 p > n）。
多次查询，但 m 的值很小（比如 m≤1e3）。

核心思路

直接利用组合数的计算公式：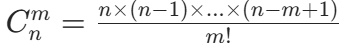

由于计算结果需要取模（组合数通常很大），而除法取模不能直接计算，因此需要用乘法逆元 来替代除法。根据费马小定理，当 p 是质数时，a 的逆元为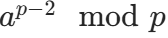（因为 a^(p-1) ≡ 1 mod p，所以 a 的逆元是 a^(p-2)）。

具体步骤：

计算分子：n×(n-1)×...×(n-m+1) mod p（共 m 项相乘）。

计算分母：m! mod p。

计算分母的乘法逆元（用快速幂实现）。

组合数结果 = 分子 × 逆元 mod p。

C++ 代码实现

cpp 复制代码

#include <iostream>
using namespace std;
typedef long long LL;

// 快速幂：计算 a^b mod p
LL qpow(LL a, LL b, LL p) {
    LL ret = 1;
    while (b) {
        if (b & 1) ret = ret * a % p; // 若b为奇数，乘上当前a
        a = a * a % p; // a平方
        b >>= 1; // b右移一位（等价于b//2）
    }
    return ret;
}

// 计算 C(n, m) mod p，p为质数且p > n
LL C(int n, int m, int p) {
    if (n < m) return 0; // 特殊情况：m > n时组合数为0
    LL up = 1, down = 1;
    // 计算分子：n*(n-1)*...*(n-m+1) mod p
    for (LL i = n - m + 1; i <= n; ++i) {
        up = up * i % p;
    }
    // 计算分母：m! mod p
    for (LL i = 2; i <= m; ++i) {
        down = down * i % p;
    }
    // 分母的逆元：down^(p-2) mod p
    LL inv_down = qpow(down, p - 2, p);
    // 组合数 = 分子 * 逆元 mod p
    return up * inv_down % p;
}

int main() {
    // 测试：计算 C(5, 2) mod 1e9+7
    int n = 5, m = 2, p = 1e9 + 7;
    cout << C(n, m, p) << endl; // 输出10
    return 0;
}

时间复杂度

单次查询 ：O (m)，因为分子和分母各需要循环 m 次，快速幂的时间复杂度是 O (log p)（p 为质数，通常是 1e9+7，log2 (p)≈30，可忽略）。

优缺点

优点：实现简单，无需预处理，适合单次查询或 m 较小的场景。

缺点：当 m 较大（比如 m=1e6）时，循环次数过多，效率较低；不适合多次查询（每次查询都要重新计算）。

方法二：杨辉三角打表（多次查询，n≤2000）

适用场景

多次查询组合数。
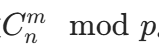n 的范围较小（n≤2000），查询次数 q 较大（比如 q≤1e6）。

核心思路

利用杨辉三角的递推公式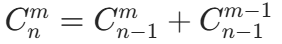：（边界条件：）。

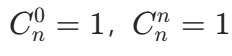提前预处理一个二维数组 f [n][m]，其中**f [n][m]**表示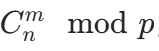，然后每次查询时直接返回 f [n][m] 即可，查询时间复杂度为 O (1)。

关键说明

杨辉三角的递推本质是动态规划：f [i][j] 表示从 i 个元素中选 j 个的组合数，它可以由 "不选第 i 个元素（从 i-1 个中选 j 个）" 和 "选第 i 个元素（从 i-1 个中选 j-1 个）" 两种情况相加得到。

由于 n≤2000，二维数组的大小是 2001×2001（约 400 万），空间占用很小，预处理时间也仅为 O (n²)（2000²=4e6 次操作），完全可以接受。

C++ 代码实现

cpp 复制代码

#include <iostream>
using namespace std;
typedef long long LL;
const int N = 2010; // n的最大值
LL f[N][N]; // f[n][m] = C(n, m) mod p

// 预处理杨辉三角，计算所有C(n, m) mod p
void get_comb(int max_n, int p) {
    // 边界条件：C(n, 0) = 1
    for (int i = 0; i <= max_n; ++i) {
        f[i][0] = 1;
    }
    // 递推计算杨辉三角
    for (int i = 1; i <= max_n; ++i) {
        // 注意：j最大为i（C(i, j)中j≤i）
        for (int j = 1; j <= i; ++j) {
            f[i][j] = (f[i-1][j] + f[i-1][j-1]) % p;
        }
    }
}

int main() {
    int max_n = 2000, p = 1e9 + 7;
    get_comb(max_n, p); // 预处理

    // 多次查询示例
    int q;
    cin >> q;
    while (q--) {
        int n, m;
        cin >> n >> m;
        // 注意：当m > n时，组合数为0
        cout << (m > n ? 0 : f[n][m]) << endl;
    }
    return 0;
}

时间复杂度

预处理 ：O (n²)（n≤2000 时，4e6 次操作，非常快）。

单次查询 ：O (1)（直接查表）。

优缺点

优点：预处理后查询极快，适合多次查询、n 较小的场景。

缺点：n 的范围受限（n≤2000），当 n 较大（比如 n=1e6）时，二维数组会超内存（2000×2000=4e6 个元素，而 1e6×1e6=1e12 个元素，完全无法存储）。

方法三：阶乘 + 逆元表（多次查询，n≤1e6）

适用场景

多次查询组合数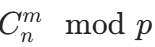（p 为质数且 p > n）。
n 的范围较大（n≤1e6），查询次数 q 较多（q≤1e6）。

核心思路

利用组合数的阶乘公式：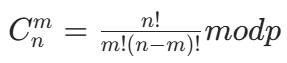

要快速计算这个公式，需要提前预处理两个数组：

阶乘数组 f ：f [i] = i! mod p（f [0]=1，f [i] = f [i-1]×i mod p）。

阶乘逆元数组 g ：g [i] = (i!)⁻¹ mod p（即 i! 的乘法逆元）。

根据费马小定理，g [n] = f [n]^(p-2) mod p（因为 n! 的逆元是 (n!)^(p-2) mod p）。而逆元数组可以从后往前递推：g [i] = (i+1) × g [i+1] mod p（推导：(i!)⁻¹ = (i+1) × (i+1)!⁻¹，因为 (i+1)! = (i+1)×i!，两边取逆元可得 (i!)⁻¹ = (i+1) × (i+1)!⁻¹）。

具体步骤：

预处理阶乘数组 f [0...max_n]。

预处理阶乘逆元数组 g [0...max_n]。

每次查询时，若 m > n 则返回 0，否则返回f [n] × g [m] % p × g [n-m] % p。

C++ 代码实现

cpp 复制代码

#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10; // n的最大值
const int MOD = 1e9 + 7; // 质数，且MOD > N
LL f[N]; // f[i] = i! mod MOD
LL g[N]; // g[i] = (i!)^{-1} mod MOD

// 快速幂：计算a^b mod p
LL qpow(LL a, LL b, LL p) {
    LL ret = 1;
    while (b) {
        if (b & 1) ret = ret * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return ret;
}

// 预处理阶乘和阶乘逆元数组
void init(int max_n) {
    // 预处理阶乘数组
    f[0] = 1;
    for (int i = 1; i <= max_n; ++i) {
        f[i] = f[i-1] * i % MOD;
    }
    // 预处理阶乘逆元数组：先计算g[max_n]，再递推
    g[max_n] = qpow(f[max_n], MOD - 2, MOD);
    for (int i = max_n - 1; i >= 0; --i) {
        g[i] = (LL)(i + 1) * g[i + 1] % MOD;
    }
}

// 计算C(n, m) mod MOD
LL C(int n, int m) {
    if (n < m) return 0;
    return f[n] * g[m] % MOD * g[n - m] % MOD;
}

int main() {
    int max_n = 1e6;
    init(max_n); // 预处理

    // 多次查询示例
    int q;
    cin >> q;
    while (q--) {
        int n, m;
        cin >> n >> m;
        cout << C(n, m) << endl;
    }
    return 0;
}

时间复杂度

预处理 ：O (n)（n≤1e6 时，1e6 次操作，很快）。

单次查询 ：O (1)（三次乘法取模）。

优缺点

优点：预处理效率高，查询速度快，适合 n 较大、多次查询的场景（n≤1e6 完全没问题）。

缺点：仅适用于 p 为质数且 p > n 的情况（如果 p ≤ n，阶乘可能与 p 不互质，逆元不存在）。

方法四：卢卡斯定理（大数值 n，p≤1e5）

适用场景

多次查询组合数。
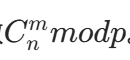n 和 m 的数值极大（比如 n≤1e18），而 p 是质数且 p≤1e5（p 可能小于 n）。

核心思路

当 n 和 m 很大（超过 1e18）时，无法直接预处理阶乘数组，此时需要用卢卡斯定理（Lucas Theorem） 来分解问题。

卢卡斯定理的核心公式：

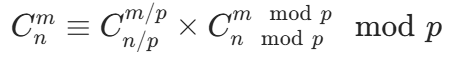
（其中 p 为质数）

通俗理解：将 n 和 m 分别表示为 p 进制数，然后对每一位分别计算组合数，最后将结果相乘取模。

具体步骤：

递归分解：将 n 和 m 分别除以 p，得到商 n'=n/p、m'=m/p，余数 r=n% p、s=m% p。

计算低位组合数 ：C (r, s) mod p（r 和 s 都小于 p，可直接用方法一计算）。

递归计算高位组合数 ：C (n', m') mod p。

结果为两者的乘积 mod p。

递归终止条件：当 m=0 时，返回 1（C (n, 0)=1）。

关键说明

卢卡斯定理的本质是**"分治"**，将大数值的组合数分解为小数值的组合数计算，而小数值的组合数可以用方法一（循环 + 逆元）快速求解。

由于 p≤1e5，每次递归计算 C (r, s) 的时间复杂度是 O (p)，而递归深度是 O (log_p n)（因为每次 n 除以 p，直到 n=0），总体时间复杂度为 O (p + log_p n)，效率很高。

C++ 代码实现

cpp 复制代码

#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10; // p的最大值
LL f[N]; // 阶乘数组，用于计算C(r, s)（r < p）
LL g[N]; // 阶乘逆元数组

// 快速幂：计算a^b mod p
LL qpow(LL a, LL b, LL p) {
    LL ret = 1;
    while (b) {
        if (b & 1) ret = ret * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return ret;
}

// 预处理阶乘和逆元数组（针对当前p）
void init(LL p) {
    int max_fact = p - 1; // 因为r = n%p < p，所以阶乘只需要预处理到p-1
    f[0] = 1;
    for (int i = 1; i <= max_fact; ++i) {
        f[i] = f[i-1] * i % p;
    }
    g[max_fact] = qpow(f[max_fact], p - 2, p);
    for (int i = max_fact - 1; i >= 0; --i) {
        g[i] = (LL)(i + 1) * g[i + 1] % p;
    }
}

// 计算C(n, m) mod p，其中n < p，m < p
LL C(LL n, LL m, LL p) {
    if (n < m) return 0;
    return f[n] * g[m] % p * g[n - m] % p;
}

// 卢卡斯定理：计算C(n, m) mod p（p为质数）
LL lucas(LL n, LL m, LL p) {
    if (m == 0) return 1; // 递归终止条件：C(n, 0) = 1
    // 分解为低位C(n%p, m%p)和高位C(n/p, m/p)
    return lucas(n / p, m / p, p) * C(n % p, m % p, p) % p;
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        LL n, m, p;
        cin >> n >> m >> p;
        init(p); // 针对当前p预处理阶乘和逆元
        cout << lucas(n, m, p) << endl;
    }
    return 0;
}

时间复杂度

预处理 ：O (p)（p≤1e5，每次查询的预处理时间可接受）。

递归查询 ：O (log_p n)（递归深度为 log_p n，每次递归计算 C (r, s) 的时间为 O (1)，因为阶乘已预处理）。

优缺点

优点：解决了大数值 n 和 m 的组合数计算问题，适用范围极广（只要 p 是质数）。

缺点：实现相对复杂，需要理解递归分治的思想；当 p 较大时（比如 p=1e5），预处理时间略长，但总体仍在可接受范围内。

三、4 种方法的场景对比与选择建议

为了方便大家在实际题目中快速选择合适的方法，这里整理了 4 种方法的核心参数对比：

方法	适用场景	时间复杂度	空间复杂度	核心限制
循环直接计算	单次查询、m 较小	O(m)	O(1)	p 为质数且 p > n
杨辉三角打表	多次查询、n≤2000	预处理 O (n²)，查询 O (1)	O(n²)	n≤2000（否则超内存）
阶乘 + 逆元表	多次查询、n≤1e6	预处理 O (n)，查询 O (1)	O(n)	p 为质数且 p > n
卢卡斯定理	多次查询、n≤1e18	预处理 O (p)，查询 O (log_p n)	O(p)	p 为质数（p 可小于 n）

选择建议

如果是单次查询，且 m 较小（比如 m≤1e3），直接用「循环直接计算」。

如果是多次查询，且 n≤2000，用「杨辉三角打表」（查询速度最快）。

如果是多次查询，且 n≤1e6、p 是质数且 p > n，用「阶乘 + 逆元表」（预处理和查询都高效）。

如果 n 和 m 是大数值（比如 1e18），或者 p≤n（p 是质数），用「卢卡斯定理」。

总结

学习组合数学，关键在于理解 "有序与无序""分类与分步" 的区别，以及灵活运用乘法逆元、快速幂、递归分治等技巧。在实际做题时，一定要先分析题目的数据范围（n、m 的大小、查询次数、p 的性质），再选择合适的方法 ------ 没有最好的方法，只有最适合的方法。

希望本文能帮助你打通组合数学的 "任督二脉"，在后续的算法学习和竞赛中披荆斩棘！如果有任何疑问或建议，欢迎在评论区留言交流～