leetcode回溯算法（90.子集Ⅱ）

if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
    continue;
}

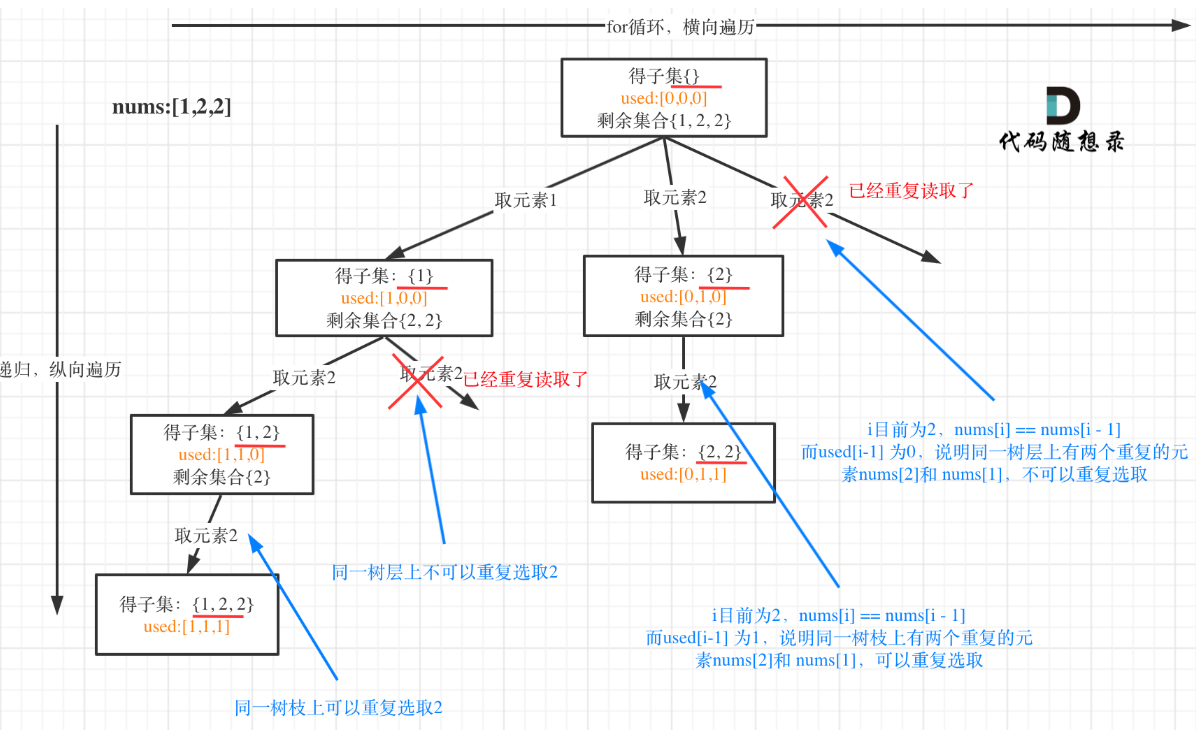
树层重复（需要跳过）：

• 在同一递归层级（同一层for循环）

• 前一个相同元素没有被选择

• 示例：在第二层，used[1]==false 且 nums[2]==nums[1]

• 应该跳过，避免重复子集

树枝重复（不需要跳过）：

• 在不同递归层级（父子关系）

• 前一个相同元素已经被选择

• 示例：在第一层选了2，在第二层遇到第二个2时，used[1]==true

• 不应该跳过，允许生成 [2,2]

所以要用uesd判断是同一树层吗。用used[i - 1] == false来判断有没有树层重复

class Solution {
private:
    vector<vector<int>> result; // 存储所有子集的结果集
    vector<int> path; // 存储当前递归路径上的子集
    
    // 回溯函数
    // nums: 输入的有重复元素的数组（已排序）
    // startIndex: 当前递归开始遍历的起始下标
    // used: 标记数组中每个元素是否在当前递归路径中被使用过
    void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
        // 每次进入递归，就把当前路径作为一个子集加入结果
        // 这保证了包括空集在内的所有子集都会被记录
        result.push_back(path);
        
        // 从startIndex开始遍历数组元素
        for (int i = startIndex; i < nums.size(); i++) {
            // 去重逻辑：跳过同一树层使用过的重复元素
            // i > 0: 确保不是第一个元素（避免越界）
            // nums[i] == nums[i - 1]: 当前元素和前一个元素相同
            // used[i - 1] == false: 前一个相同元素在当前层没有被使用
            // 这个条件表示前一个相同元素在同一树层已经使用过，需要跳过
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue; // 跳过当前重复元素
            }
            
            // 选择当前元素加入路径
            path.push_back(nums[i]);
            used[i] = true; // 标记当前元素已使用
            
            // 递归进入下一层，从i+1开始（避免重复使用同一个元素）
            backtracking(nums, i + 1, used);
            
            // 回溯：撤销选择
            used[i] = false; // 取消标记
            path.pop_back(); // 从路径中移除当前元素
        }
    }

public:
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        // 清空全局变量，防止多次调用时结果残留
        result.clear();
        path.clear();
        
        // 初始化used数组，所有元素初始状态为未使用
        vector<bool> used(nums.size(), false);
        
        // 关键步骤：先排序，使得相同元素相邻，便于去重
        sort(nums.begin(), nums.end());
        
        // 开始回溯
        backtracking(nums, 0, used);
        
        // 返回所有子集
        return result;
    }
};

核心逻辑解释：

1. 排序：先对数组排序，使相同元素相邻，便于识别重复元素。

2. used数组的作用：

   • used[i] == true：表示元素nums[i]在**当前递归路径（树枝）**中被使用

   • used[i] == false：表示元素nums[i]在**当前层（树层）**未被使用

   • 通过判断used[i-1] == false可以知道前一个相同元素是否在同一层被使用过

3. 去重逻辑：

   • 当nums[i] == nums[i-1]且used[i-1] == false时，说明前一个相同元素已经在本层考虑过，当前元素应该跳过

   • 这样可以避免生成重复的子集，如[1,2,2']和[1,2',2]

4. 递归过程：

   • 每次递归先记录当前路径（子集）

   • 从startIndex开始遍历，避免重复使用元素

   • 选择元素 → 递归 → 撤销选择（回溯）

以 nums = [1,2,2] 为例，详细跟踪代码执行流程

初始化

nums = [1, 2, 2]  // 输入
sort(nums)        // 排序后仍是 [1, 2, 2]
used = [false, false, false]
result = []
path = []

调用 backtracking(nums, 0, used)

result.push_back(path) → result = [[]]  // 添加空集
for循环，i=0 nums[0]=1
if条件不满足
path.push_back(1)   // path = [1]
used[0] = true   // used = [true, false, false]
递归调用 backtracking(nums, 1, used)

调用 backtracking(nums, 1, used)

result.push_back(path) → result = [[], [1]]
for循环，i=1 nums[1]=2
if条件不满足
path.push_back(2) → path = [1, 2]
used[1] = true   // used = [true, true, false]
递归调用 backtracking(nums, 2, used)

调用 backtracking(nums, 2, used)

result.push_back(path) → result = [[], [1], [1, 2]]
for循环，i=2 nums[2]=2
if判断：i>0 && nums[2]==nums[1] && used[1]==false → true && 2==2 && false → false4
所以不执行if语句
path.push_back(2) → path = [1, 2, 2]
used[2] = true   // used = [true, true, true]
递归调用 backtracking(nums, 3, used)

调用 backtracking(nums, 3, used)

result.push_back([1, 2, 2]) → result = [[], [1], [1, 2], [1, 2, 2]]
for循环 i = 3 开始：不满足 i < nums.size()，直接结束

返回backtracking(nums, 2, used)

used[2] = false    // 现在used = [true, true, false]
path.pop_back() → path = [1, 2]
i++ 使i变为3，for循环条件 i < nums.size()为false，所以for循环结束

返回backtracking(nums, 1, used)

used[1] = false    // 现在used = [true, false, false]
path.pop_back() → 之前的path = [1, 2]
现在的path = [1]  // 注意：刚从[1,2]变为[1]
i++→ i变为2（i=2）

继续for循环

if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
    continue;
}

2>0  &&  nums[2]==nums[1]  &&  used[1]==false
true &&      true          &&   true = true
所以执行if语句，执行continue，即跳过当前循环

path.push_back(nums[i]);       // 不会执行
used[i] = true;                // 不会执行
backtracking(nums, i + 1, used); // 不会执行
used[i] = false;               // 不会执行
path.pop_back();               // 不会执行

i++执行 → i从2变为3
i=3 < nums.size()=3 → false，不满足for循环条件，所以结束for循环

场景	**continue**的效果	break 的效果
i=2时触发条件	跳过i=2，继续i=3	终止整个for循环
循环是否继续	继续执行i=3的迭代	循环立即结束
后续代码执行	执行i++，检查条件	不执行i++，直接结束循环
对结果的影响	只跳过重复元素	跳过当前及后面的所有元素

返回backtracking(nums, 0, used)

used[0] = false;  // 回溯
path.pop_back();   // 回溯
回溯后的状态：
path = []                  // 之前path=[1]   pop_back后变为空[]
used = [false, false, false]  // used[0]刚被设为false

i=0的循环体执行完毕
i++执行 → i从0变为1i=1不满足if条件判断，不执行if语句
path.push_back(nums[1]);  // nums[1] = 2
所以现在path = [2] 
used[1] = true;   // used = [false, true, false]

递归调用backtracking(nums, 2, used)

result.push_back(path);  // 添加当前path到结果

result从 [[], [1], [1,2], [1,2,2]] 
变为  [[], [1], [1,2], [1,2,2], [2]]

.........

.........

.........