本文介绍3D测量领域表示测量质量的基础术语。准确理解这些术语,对测量结果的分析与量化评估至关重要。作为基础概念,这些术语应具有明确定义。然而受学科差异、翻译、时间迁移等因素的影响,个别术语存在定义偏差。本文将对这些术语的含义进行系统解析,使读者有更全面的认识。
系统误差(Systematic error)和随机误差(Random error)
先介绍无歧义的概念------误差(Error)。误差的定义是:测量值与真实值之间的差异 。
假定测量值为 f ^ \hat f f^,真值为 f f f,则误差表示为 Error = f ^ − f \text{Error} = \hat f - f Error=f^−f实际测量时通常可以观察到,即使对同一个物理量进行测量,测量值也会存在随机的波动。为了更准确的刻画测量结果的好坏,通常取多次测量误差平方的均值,即MSE(Mean square error)作为度量标准
MSE = 1 N ∑ n ( f ^ n − f ) 2 \text{MSE} = \frac{1}{N}\sum_n(\hat f_n-f)^2 MSE=N1n∑(f^n−f)2可以将测量值看成是一个随机变量,用期望和方差来表征测量值的统计特性。令 E [ f ^ ] E[\hat f] E[f^]表示测量值的期望, D [ f ^ ] = E [ ( f ^ − E [ f ^ ] ) 2 ] = E [ f ^ 2 ] − E [ f ^ ] 2 D[\hat f]=E[(\hat f -E[\hat f])^2]=E[\hat f^2]-E[\hat f]^2 D[f^]=E[(f^−E[f^])2]=E[f^2]−E[f^]2表示测量值的方差,则测量值的均方误差MSE表示为
MSE = E [ ( f ^ − f ) 2 ] = E [ f ^ 2 ] − 2 E [ f ^ f ] + E [ f 2 ] = E [ f ^ ] 2 + D [ f ^ ] − 2 E [ f ^ ] f + f 2 = ( E [ f ^ ] − f ) 2 + D [ f ^ ] \text{MSE} = E[(\hat f -f)^2] \\=E[\hat f^2]-2E[\hat ff]+E[f^2]\\=E[\hat f]^2+D[\hat f]-2E[\hat f]f+f^2\\=(E[\hat f]-f)^2+D[\hat f] MSE=E[(f^−f)2]=E[f^2]−2E[f^f]+E[f2]=E[f^]2+D[f^]−2E[f^]f+f2=(E[f^]−f)2+D[f^]可以看到,MSE的贡献可以分为两项。第一项,由多次测量的均值与真值的误差决定,即理想无噪声情况下测量值的偏差,这项误差为系统误差(Systematic error) 。第二项,由多次测量值本身的方差决定,这项误差为随机误差(Random error) 。系统误差和随机误差的和称为总误差(Total error) 。
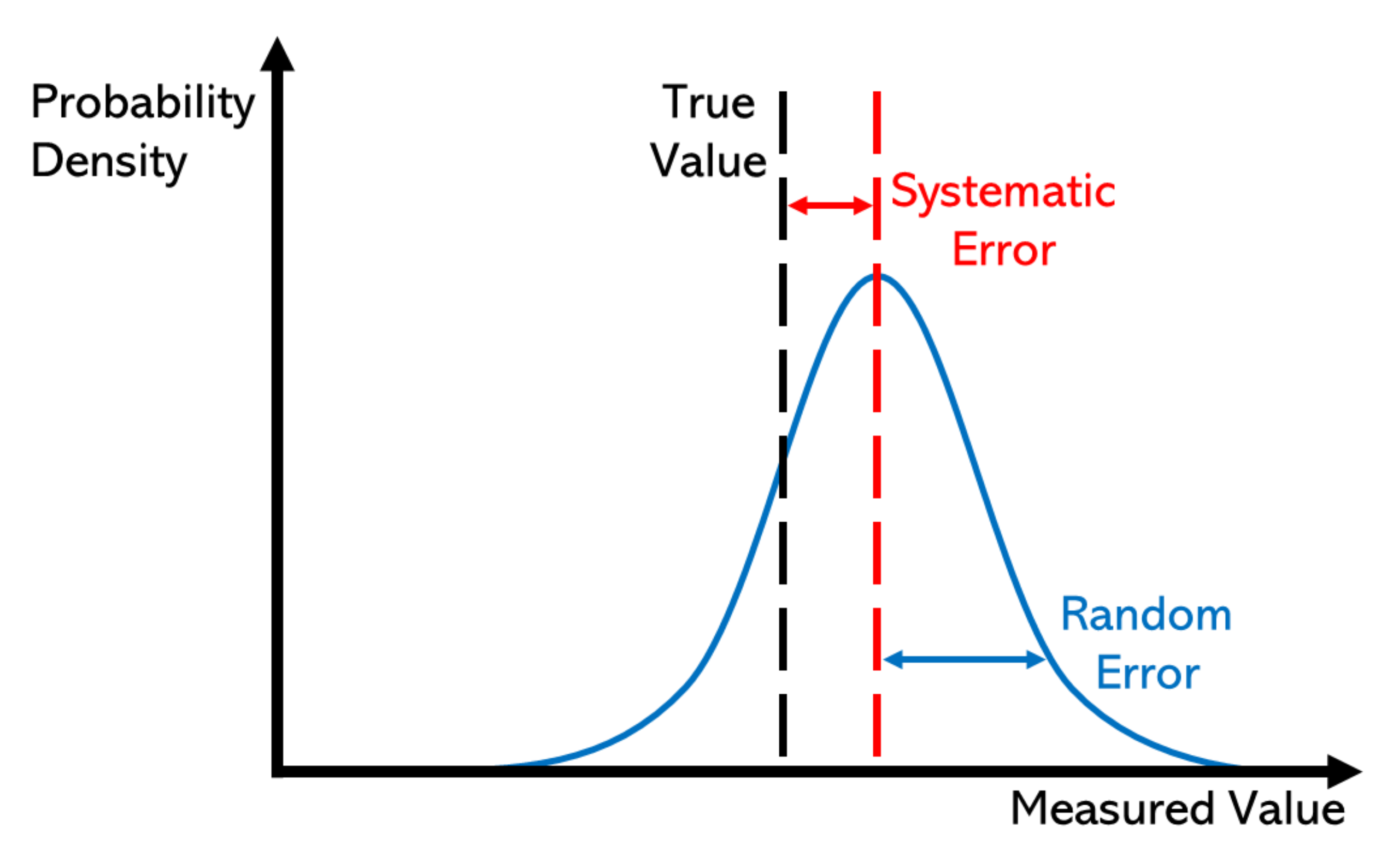
为降低测量的总误差,需要弄清楚各项误差的来源,并根据其导致的误差类型进行处理。以条纹结构光系统为例,相机镜头的安装偏差、镜头本身的畸变、相机和投影装置的位置安装偏差、投影条纹的非正弦性失真、投影镜头的畸变等因素导致的误差即使在无测量噪声的情况下仍然存在,因此属于系统误差。系统误差通常可以通过标定进行校正补偿。信号光、环境光导致的相机散粒噪声、相机本身存在的暗噪声等属于随机误差。随机误差则可以通过算法上的滤波、提升测量信噪比等多种途径进行抑制。
精密度Precision和准确度Accuracy
Precision和Accuracy是对测量结果质量的定性描述。
精密度(Precision) 指多次测量值彼此之间的接近程度。精密度衡量了随机误差。
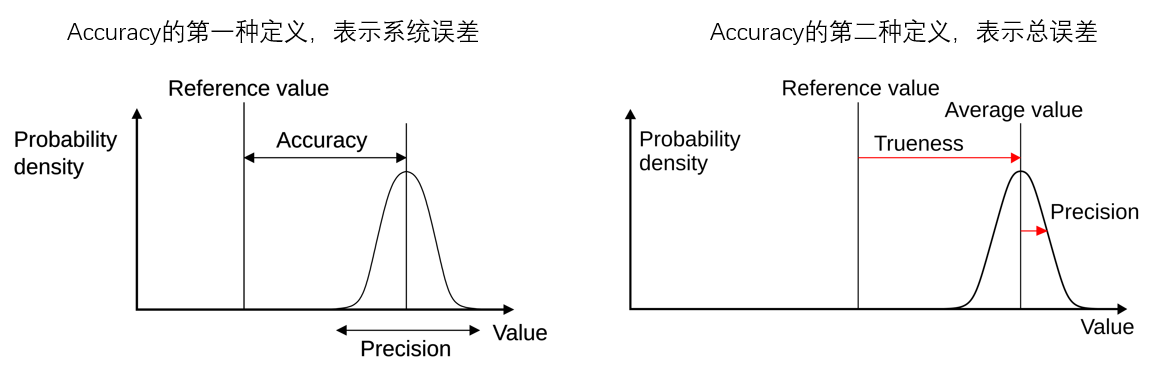
准确度(Accuracy) 指测量值与真实值之间的接近程度。准确度有两种不同的含义。一般情况下,准确表示多次测量平均值与真实值的接近程度,即系统误差。而在ISO标准中,准确度指总误差,系统误差则由 正确度(Trueness) 描述【1,2】。下图是准确度两种不同定义的图示。在看论文查资料时,遇到Accuracy这个词要注意区分作者使用的具体是那种定义,以正确理解作者意图。
【2】Understanding the meaning of accuracy, trueness and precision