目录
[1.1 算法起源与定位](#1.1 算法起源与定位)
[1.2 关键定义与指标](#1.2 关键定义与指标)
[3.1 阶段一:频繁项集挖掘(核心步骤)](#3.1 阶段一:频繁项集挖掘(核心步骤))
[步骤 1:初始化 ------ 挖掘 1 - 频繁项集 (L₁)](#步骤 1:初始化 —— 挖掘 1 - 频繁项集 (L₁))
[步骤 2:迭代生成 k - 频繁项集(k≥2)](#步骤 2:迭代生成 k - 频繁项集(k≥2))
[3.2 阶段二:关联规则生成](#3.2 阶段二:关联规则生成)
[4.1 示例数据集(购物篮数据)](#4.1 示例数据集(购物篮数据))
[4.2 频繁项集挖掘过程(min_sup=0.6,即≥3 个事务)](#4.2 频繁项集挖掘过程(min_sup=0.6,即≥3 个事务))
[4.3 关联规则生成(min_conf=0.8)](#4.3 关联规则生成(min_conf=0.8))
[五、Python 实现示例(使用 mlxtend 库)](#五、Python 实现示例(使用 mlxtend 库))
[6.1 优点](#6.1 优点)
[6.2 缺点](#6.2 缺点)
[7.1 典型应用场景](#7.1 典型应用场景)
[7.2 常见优化算法](#7.2 常见优化算法)
一、算法概述与核心概念
1.1 算法起源与定位
Apriori 算法是由 Rakesh Agrawal 和 Ramakrishnan Srikant 于 1994 年提出的关联规则挖掘经典算法,其名称源自拉丁语 "a priori"(意为 "来自先前的知识"),体现了算法利用频繁项集先验性质进行剪枝的核心思想。它是数据挖掘十大经典算法之一,主要用于从大规模事务数据集中发现项集之间的关联关系,最著名的应用场景就是 "啤酒与尿布" 的超市购物篮分析案例。
1.2 关键定义与指标
| 术语 | 定义 | 计算公式 |
|---|---|---|
| 事务 (Transaction) | 数据库中的一条记录,如一次购物的商品清单 | - |
| 项 (Item) | 事务中的基本单位,如一件商品 | - |
| 项集 (Itemset) | 若干项的集合,k 个项的集合称为 k - 项集 | - |
| 支持度 (Support) | 包含项集的事务数占总事务数的比例,衡量项集的普遍性 | Support (X) = (包含 X 的事务数)/(总事务数) |
| 置信度 (Confidence) | 事务包含 X 时也包含 Y 的概率,衡量规则 X→Y 的可靠性 | Confidence(X→Y) = Support(X∪Y) / Support(X) |
| 频繁项集 (Frequent Itemset) | 支持度≥最小支持度阈值 (min_sup) 的项集 | - |
| 强关联规则 (Strong Rule) | 同时满足最小支持度和最小置信度 (min_conf) 的关联规则 | - |
| 提升度 (Lift) | 规则 X→Y 的置信度与 Y 的支持度之比,衡量规则的有效性 | Lift(X→Y) = Confidence(X→Y) / Support(Y) |
二、核心原理:先验性质与反单调性
Apriori 算法的核心在于利用先验原理(Apriori Property)大幅减少计算量,该原理包含两个方向:
- 正向性质 :如果一个项集是频繁的,那么它的所有子集也一定是频繁的(支持度不会因项数减少而降低)
- 反向性质(反单调性) :如果一个项集是非频繁 的,那么它的所有超集也一定是非频繁的(支持度不会因项数增加而提高)
这一性质允许算法在搜索过程中进行剪枝,即一旦发现某个项集是非频繁的,就可以立即丢弃其所有超集,无需再计算,从而显著减少候选项集的数量。
三、算法完整流程
Apriori 算法分为两大核心阶段:频繁项集挖掘 和关联规则生成,整体采用逐层迭代的搜索策略。
3.1 阶段一:频繁项集挖掘(核心步骤)
该阶段通过 "生成 - 计数 - 剪枝" 的循环,从 1 - 项集逐步扩展到 k - 项集,直到无法生成新的频繁项集。
步骤 1:初始化 ------ 挖掘 1 - 频繁项集 (L₁)
- 扫描数据库,计算所有单个项的支持度
- 筛选出支持度≥min_sup 的项,形成 1 - 频繁项集 L₁
步骤 2:迭代生成 k - 频繁项集(k≥2)
循环执行以下子步骤,直到 Lₖ为空:
-
连接操作 (Join):通过自连接 Lₖ₋₁生成候选 k - 项集 Cₖ
- 规则:两个 (k-1)- 项集前 k-2 个项相同,仅最后一个项不同时才进行连接
- 示例:{A,B} 和 {A,C} 连接生成 {A,B,C}
-
剪枝操作 (Prune):利用先验性质去除 Cₖ中的非频繁候选项集
- 规则:检查每个候选 k - 项集的所有 (k-1)- 子集是否都在 Lₖ₋₁中,若有不在的则剪枝掉
- 示例:候选集 {A,B,C,D} 的子集 {A,B,D} 不在 L₃中,则剪枝掉该候选集
-
支持度计数:扫描数据库,计算 Cₖ中每个候选项集的支持度
-
筛选频繁项集:保留 Cₖ中支持度≥min_sup 的项集,形成 Lₖ
3.2 阶段二:关联规则生成
基于挖掘出的所有频繁项集,生成满足 min_conf 的强关联规则:
-
对每个频繁项集 F:
- 生成 F 的所有非空真子集
- 对每个子集 S,计算规则 S→(F-S) 的置信度
- 保留置信度≥min_conf 的规则作为强关联规则
-
优化策略:利用置信度的反单调性 ------ 如果规则 S→(F-S) 不满足 min_conf,则所有 S'⊂S 的规则 S'→(F-S') 也不满足 min_conf,可提前剪枝
四、算法示例演示
4.1 示例数据集(购物篮数据)
| 事务 ID | 购买商品 |
|---|---|
| T1 | 牛奶,面包,尿布 |
| T2 | 可乐,面包,尿布,啤酒 |
| T3 | 牛奶,尿布,啤酒,鸡蛋 |
| T4 | 面包,牛奶,尿布,啤酒 |
| T5 | 面包,牛奶,尿布,可乐 |
4.2 频繁项集挖掘过程(min_sup=0.6,即≥3 个事务)
-
L₁:{牛奶 (4), 面包 (4), 尿布 (5), 可乐 (2), 啤酒 (3)} → 剪去可乐 → {牛奶,面包,尿布,啤酒}
-
C₂:自连接生成 6 个候选集 → 剪枝后 → 扫描计数 → L₂:{牛奶,面包 (3), 牛奶,尿布 (4), 面包,尿布 (4), 尿布,啤酒 (3)}
-
C₃:自连接生成候选集 → 剪枝 → 扫描计数 → L₃:{牛奶,面包,尿布 (3), 牛奶,尿布,啤酒 (3)}
-
C₄:生成候选集 {牛奶,面包,尿布,啤酒} → 剪枝(子集 {面包,啤酒} 不在 L₂)→ 无频繁项集,结束
4.3 关联规则生成(min_conf=0.8)
以频繁项集 {牛奶,尿布,啤酒} 为例:
- 规则 {牛奶,尿布}→{啤酒}:置信度 = 3/4=0.75 < 0.8 → 不保留
- 规则 {牛奶,啤酒}→{尿布}:置信度 = 3/3=1.0 ≥ 0.8 → 保留
- 规则 {尿布,啤酒}→{牛奶}:置信度 = 3/3=1.0 ≥ 0.8 → 保留
- 规则 {牛奶}→{尿布,啤酒}:置信度 = 3/4=0.75 < 0.8 → 不保留
- 规则 {尿布}→{牛奶,啤酒}:置信度 = 3/5=0.6 < 0.8 → 不保留
- 规则 {啤酒}→{牛奶,尿布}:置信度 = 3/3=1.0 ≥ 0.8 → 保留
五、Python 实现示例(使用 mlxtend 库)
python
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import apriori, association_rules
import pandas as pd
# 1. 准备数据
dataset = [
['牛奶', '面包', '尿布'],
['可乐', '面包', '尿布', '啤酒'],
['牛奶', '尿布', '啤酒', '鸡蛋'],
['面包', '牛奶', '尿布', '啤酒'],
['面包', '牛奶', '尿布', '可乐']
]
# 2. 数据编码
te = TransactionEncoder()
te_ary = te.fit(dataset).transform(dataset)
df = pd.DataFrame(te_ary, columns=te.columns_)
# 3. 挖掘频繁项集(min_sup=0.6)
frequent_itemsets = apriori(df, min_support=0.6, use_colnames=True)
print("频繁项集:")
print(frequent_itemsets)
# 4. 生成关联规则(min_conf=0.8)
rules = association_rules(frequent_itemsets, metric="confidence", min_threshold=0.8)
print("\n强关联规则:")
print(rules[['antecedents', 'consequents', 'support', 'confidence', 'lift']])程序运行结果展示
频繁项集:
support itemsets
0 0.6 frozenset({啤酒})
1 1.0 frozenset({尿布})
2 0.8 frozenset({牛奶})
3 0.8 frozenset({面包})
4 0.6 frozenset({尿布, 啤酒})
5 0.8 frozenset({尿布, 牛奶})
6 0.8 frozenset({尿布, 面包})
7 0.6 frozenset({牛奶, 面包})
8 0.6 frozenset({尿布, 面包, 牛奶})
强关联规则:
antecedents consequents support confidence lift
0 frozenset({啤酒}) frozenset({尿布}) 0.6 1.0 1.0
1 frozenset({尿布}) frozenset({牛奶}) 0.8 0.8 1.0
2 frozenset({牛奶}) frozenset({尿布}) 0.8 1.0 1.0
3 frozenset({尿布}) frozenset({面包}) 0.8 0.8 1.0
4 frozenset({面包}) frozenset({尿布}) 0.8 1.0 1.0
5 frozenset({牛奶, 面包}) frozenset({尿布}) 0.6 1.0 1.0
六、算法优缺点分析
6.1 优点
- 原理简单易懂:基于先验性质的剪枝策略逻辑清晰,易于实现和理解
- 结果可靠:通过支持度和置信度双重阈值筛选,确保挖掘出的规则具有普遍性和可靠性
- 适用性广:可应用于各类事务数据,如零售、医疗、网络日志等领域
- 可解释性强:生成的关联规则直观易懂,便于业务人员理解和应用
6.2 缺点
- 性能瓶颈:多次扫描数据库,随着项数增加,候选项集数量呈指数级增长,效率低下
- 内存消耗大:需要存储大量候选项集和频繁项集,不适合超大规模数据集
- 阈值敏感:min_sup 和 min_conf 的选择对结果影响显著,需要领域知识和反复调试
- 规则冗余:可能生成大量相似规则,需要进一步筛选和优化
七、应用场景与优化方向
7.1 典型应用场景
- 零售行业:购物篮分析,商品摆放优化,交叉销售推荐(如 "啤酒与尿布")
- 电商平台:个性化推荐系统,基于用户购买历史推荐相关商品
- 医疗领域:疾病与症状关联分析,药物副作用关联挖掘
- 金融领域:信用卡欺诈检测,客户消费模式分析
- 网络安全:异常访问模式识别,入侵检测规则挖掘
7.2 常见优化算法
针对 Apriori 的性能问题,研究者提出了多种改进算法:
- FP-Growth:采用频繁模式树(FP-Tree)结构,仅需两次扫描数据库,效率大幅提升
- Eclat:基于垂直数据格式,利用集合交集计算支持度,适合稀疏数据集
- AprioriTID:用事务标识符代替原始数据,减少后续扫描的数据量
- AprioriHybrid:结合 Apriori 和 AprioriTID 的优点,平衡内存使用和扫描效率
八、无第三方库的Apriori算法实战
(一)准备数据集TXT文件,可以命名为"apriori_random_transactions.txt",也可以替换成其他TXT文件名。
bash
矿泉水,薯片,酸奶,面包,鸡蛋
啤酒,尿布,面包,鸡蛋
可乐,啤酒,尿布,牛奶,面包
啤酒,尿布,牛奶,酸奶,面包
可乐,啤酒,尿布,牛奶,薯片
可乐,啤酒,面包,鸡蛋
啤酒,尿布,牛奶,矿泉水
啤酒,尿布,面包
可乐,啤酒,矿泉水,酸奶
啤酒,尿布,火腿肠,牛奶,面包
可乐,尿布,矿泉水
可乐,啤酒,牛奶,酸奶
啤酒,牛奶,薯片,酸奶,面包
可乐,尿布,牛奶,面包,鸡蛋
可乐,啤酒,尿布,面包
可乐,啤酒,尿布,酸奶,鸡蛋
可乐,啤酒,火腿肠,薯片,面包
啤酒,尿布,牛奶,矿泉水,面包
啤酒,尿布,牛奶,酸奶
啤酒,尿布,火腿肠,牛奶,面包,鸡蛋
啤酒,尿布,矿泉水,酸奶,面包
啤酒,尿布,火腿肠,牛奶
尿布,牛奶,矿泉水,酸奶,鸡蛋
啤酒,尿布,酸奶,面包
尿布,火腿肠,牛奶,鸡蛋
可乐,尿布,牛奶,矿泉水
啤酒,火腿肠,矿泉水,薯片,面包
啤酒,尿布,牛奶,薯片,鸡蛋
矿泉水,酸奶,面包
牛奶,矿泉水,鸡蛋
可乐,啤酒,尿布,牛奶,酸奶,面包
啤酒,牛奶,矿泉水,薯片,面包
可乐,啤酒,尿布,酸奶,面包
可乐,尿布,薯片,鸡蛋
可乐,火腿肠,面包
可乐,尿布,矿泉水,薯片,鸡蛋
啤酒,尿布,酸奶,鸡蛋
可乐,火腿肠,酸奶,鸡蛋
啤酒,尿布,牛奶,鸡蛋
尿布,火腿肠,牛奶,薯片,鸡蛋
牛奶,酸奶,面包
啤酒,火腿肠,牛奶,矿泉水,酸奶
啤酒,尿布,火腿肠,面包
啤酒,尿布,薯片,面包
可乐,牛奶,鸡蛋
啤酒,尿布,酸奶
可乐,尿布,薯片,面包,鸡蛋
可乐,啤酒,尿布,矿泉水,面包
啤酒,尿布,牛奶,面包,鸡蛋
尿布,薯片,酸奶,面包,鸡蛋
啤酒,尿布,牛奶,矿泉水,酸奶,面包
啤酒,尿布,牛奶,薯片,面包
啤酒,尿布,薯片,酸奶,面包
火腿肠,牛奶,薯片,鸡蛋
可乐,啤酒,尿布,牛奶
可乐,啤酒,尿布,牛奶,酸奶
啤酒,尿布,牛奶,矿泉水,薯片,面包
啤酒,尿布,牛奶,面包
啤酒,尿布,牛奶
可乐,牛奶,薯片,面包,鸡蛋
尿布,火腿肠,鸡蛋
矿泉水,面包,鸡蛋
啤酒,尿布,牛奶,薯片
可乐,啤酒,尿布,薯片,酸奶
矿泉水,酸奶,面包
火腿肠,矿泉水,薯片,酸奶,面包
可乐,尿布,矿泉水,面包
尿布,牛奶,酸奶,面包
啤酒,火腿肠,牛奶
可乐,尿布,牛奶,薯片,面包
牛奶,矿泉水,面包
啤酒,火腿肠,牛奶,矿泉水,薯片
可乐,尿布,薯片,鸡蛋
啤酒,火腿肠,牛奶,薯片,酸奶
啤酒,火腿肠,面包
可乐,啤酒,酸奶
可乐,尿布,薯片
可乐,啤酒,牛奶,面包,鸡蛋
火腿肠,薯片,酸奶,鸡蛋
可乐,啤酒,薯片,面包
啤酒,尿布,薯片,酸奶,面包
啤酒,面包,鸡蛋
啤酒,尿布,牛奶,面包
可乐,啤酒,牛奶,酸奶,鸡蛋
啤酒,尿布,火腿肠,薯片,面包
尿布,火腿肠,矿泉水,薯片,酸奶
可乐,尿布,牛奶,薯片
可乐,牛奶,鸡蛋
可乐,薯片,酸奶,面包,鸡蛋
啤酒,牛奶,酸奶,鸡蛋
啤酒,牛奶,矿泉水,薯片,鸡蛋
可乐,尿布,火腿肠,鸡蛋
可乐,牛奶,薯片
啤酒,火腿肠,矿泉水,面包,鸡蛋
可乐,啤酒,薯片
火腿肠,矿泉水,薯片
可乐,矿泉水,酸奶
可乐,尿布,牛奶,酸奶
矿泉水,薯片,面包,鸡蛋
火腿肠,矿泉水,薯片,酸奶,面包(二)无第三方库的Apriori算法的Python代码完整实现
python
import os
import sys
from collections import defaultdict
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import numpy as np
# 3D绘图必备库
from mpl_toolkits.mplot3d import Axes3D
# ===================== 全局配置:Matplotlib中文显示+样式美化 =====================
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans'] # 解决中文乱码(SimHei=黑体,适配Windows)
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
plt.rcParams['figure.facecolor'] = 'white' # 画布背景色
plt.rcParams['axes.facecolor'] = '#f8f9fa' # 坐标轴背景色
plt.rcParams['grid.alpha'] = 0.3 # 网格透明度
plt.rcParams['savefig.dpi'] = 300 # 保存图片高清DPI
plt.rcParams['figure.dpi'] = 100 # 显示图片DPI
plt.rcParams['font.size'] = 10 # 全局字体大小
# 定义配色方案(贴合数据分析)
COLORS = ['#2E86AB', '#A23B72', '#F18F01', '#C73E1D', '#7209B7', '#0B4F6C']
# 关联类型配色
REL_COLORS = {
"强正关联": "#C73E1D",
"弱正关联": "#F18F01",
"无关联/负关联": "#2E86AB"
}
# ===================== 全局工具函数(辅助功能)=====================
def print_separator(char="-", length=80, title=""):
"""打印分隔线,美化输出(可视化基础)"""
if title:
print(f"{char * ((length - len(title) - 2) // 2)} {title} {char * ((length - len(title) - 2) // 2)}")
else:
print(char * length)
def format_table(headers, rows, align="left"):
"""格式化生成文本表格(核心可视化函数)"""
col_widths = [len(str(h)) for h in headers]
for row in rows:
for i, val in enumerate(row):
val_len = len(str(val))
if val_len > col_widths[i]:
col_widths[i] = val_len
align_fun = {
"left": lambda s, w: str(s).ljust(w),
"right": lambda s, w: str(s).rjust(w),
"center": lambda s, w: str(s).center(w)
}[align]
table = [' | '.join([align_fun(h, col_widths[i]) for i, h in enumerate(headers)])]
table.append(' | '.join(["-" * w for w in col_widths]))
for row in rows:
table.append(' | '.join([align_fun(val, col_widths[i]) for i, val in enumerate(row)]))
return "\n".join(table)
def text_bar_chart(data, title, x_label, y_label, max_bar_len=50):
"""生成文本柱状图(可视化统计分布)"""
if not data:
return f"{title}\n暂无数据"
max_val = max(data.values())
bar_data = {k: int(v / max_val * max_bar_len) if max_val != 0 else 0 for k, v in data.items()}
chart = [f"【{title}】", f"{y_label:>10} | {x_label:<{max_bar_len}} (数值)"]
chart.append("-" * (12 + max_bar_len + 8))
for k, v in sorted(data.items(), key=lambda x: x[1], reverse=True):
bar = "■" * bar_data[k]
chart.append(f"{str(k):>10} | {bar:<{max_bar_len}} ({v})")
return "\n".join(chart)
# ===================== 数据加载与清洗模块 =====================
def load_transactions(data_source="test", file_path=None):
"""加载并清洗事务数据"""
raw_transactions = []
if data_source == "test":
raw_transactions = [
"牛奶,面包,尿布",
"可乐,面包,尿布,啤酒",
"牛奶,尿布,啤酒,鸡蛋",
"面包,牛奶,尿布,啤酒",
"面包,牛奶,尿布,可乐",
"牛奶,面包,啤酒",
"尿布,啤酒,可乐",
"面包,尿布,啤酒"
]
print_separator(title="加载内置测试数据(购物篮数据)")
elif data_source == "file":
if not file_path or not os.path.exists(file_path):
raise FileNotFoundError(f"文件路径无效:{file_path}")
with open(file_path, "r", encoding="utf-8") as f:
raw_transactions = [line.strip() for line in f if line.strip()]
print_separator(title=f"加载本地文件:{os.path.basename(file_path)}")
else:
raise ValueError("数据来源仅支持:test(内置测试)/file(本地文件)")
clean_transactions = []
all_items = set()
for line in raw_transactions:
items = [item.strip() for item in line.replace(" ", ",").replace("\t", ",").split(",")]
valid_items = set([item for item in items if item])
if valid_items:
clean_transactions.append(valid_items)
all_items.update(valid_items)
print(f"原始事务数:{len(raw_transactions)} | 清洗后有效事务数:{len(clean_transactions)}")
print(f"数据集中唯一项总数:{len(all_items)} | 所有项:{sorted(all_items)}")
return clean_transactions, sorted(all_items)
# ===================== Apriori核心算法模块(频繁项集挖掘)=====================
def calculate_support(transaction_set, itemset, total_trans):
"""计算项集的支持度"""
if total_trans == 0:
return 0.0, 0
itemset = set(itemset)
count = 0
for trans in transaction_set:
if itemset.issubset(trans):
count += 1
support = round(count / total_trans, 4)
return support, count
def create_c1(all_items):
"""生成1-候选项集C1"""
return [(item,) for item in all_items]
def apriori_gen(frequent_k_1, k):
"""连接+剪枝,生成k-候选项集Ck"""
Ck = []
len_fk1 = len(frequent_k_1)
for i in range(len_fk1):
for j in range(i + 1, len_fk1):
list_i = list(frequent_k_1[i])[:k - 2]
list_j = list(frequent_k_1[j])[:k - 2]
if list_i == list_j:
new_itemset = tuple(sorted(set(frequent_k_1[i]) | set(frequent_k_1[j])))
if len(new_itemset) == k:
Ck.append(new_itemset)
pruned_Ck = []
frequent_k_1_set = set(frequent_k_1)
for candidate in Ck:
subsets = []
for i in range(len(candidate)):
subset = tuple(sorted(set(candidate) - {candidate[i]}))
subsets.append(subset)
if all(s in frequent_k_1_set for s in subsets):
pruned_Ck.append(candidate)
return pruned_Ck
def get_frequent_itemsets(transaction_set, min_support):
"""逐层挖掘所有频繁项集"""
total_trans = len(transaction_set)
if total_trans == 0:
return {}, 0
all_items = sorted({item for trans in transaction_set for item in trans})
frequent_itemsets = defaultdict(list)
k = 1
C1 = create_c1(all_items)
L1 = []
for itemset in C1:
support, _ = calculate_support(transaction_set, itemset, total_trans)
if support >= min_support:
L1.append((itemset, support))
if not L1:
return frequent_itemsets, total_trans
frequent_itemsets[k] = L1
print_separator(title=f"挖掘到{len(L1)}个1-频繁项集")
while True:
k += 1
frequent_k_1 = [itemset for itemset, sup in frequent_itemsets[k - 1]]
Ck = apriori_gen(frequent_k_1, k)
if not Ck:
break
Lk = []
for candidate in Ck:
support, _ = calculate_support(transaction_set, candidate, total_trans)
if support >= min_support:
Lk.append((candidate, support))
if not Lk:
break
frequent_itemsets[k] = Lk
print_separator(title=f"挖掘到{len(Lk)}个{k}-频繁项集")
return frequent_itemsets, total_trans
# ===================== 关联规则生成模块 =====================
def generate_association_rules(frequent_itemsets, transaction_set, total_trans, min_confidence):
"""基于频繁项集生成强关联规则"""
strong_rules = []
for k in frequent_itemsets:
if k < 2:
continue
for itemset, sup_XY in frequent_itemsets[k]:
itemset_set = set(itemset)
subsets = []
def dfs(remaining, current):
if current and remaining:
subsets.append(tuple(sorted(current)))
for i in range(len(remaining)):
dfs(remaining[i + 1:], current + [remaining[i]])
dfs(sorted(itemset_set), [])
for S in subsets:
S_set = set(S)
Y_set = itemset_set - S_set
Y = tuple(sorted(Y_set))
sup_S, _ = calculate_support(transaction_set, S, total_trans)
if sup_S == 0:
continue
confidence = round(sup_XY / sup_S, 4)
sup_Y, _ = calculate_support(transaction_set, Y, total_trans)
lift = round(confidence / sup_Y if sup_Y != 0 else 0, 4)
support = sup_XY
if confidence >= min_confidence:
strong_rules.append((S, Y, support, confidence, lift))
strong_rules = list(set(strong_rules))
strong_rules.sort(key=lambda x: x[4], reverse=True)
return strong_rules
# ===================== 纯文本可视化模块 =====================
def visualize_analysis_result(transaction_set, frequent_itemsets, strong_rules, total_trans):
"""纯文本可视化所有分析结果"""
all_items = sorted({item for trans in transaction_set for item in trans})
print_separator(char="=", title="Apriori算法分析结果可视化报告", length=100)
print_separator(title="一、数据基本概览")
data_overview = [
["总事务数", total_trans],
["有效事务数", len(transaction_set)],
["唯一项总数", len(all_items)],
["数据稀疏度", f"{round(1 - sum(len(t) for t in transaction_set) / (total_trans * len(all_items)), 4) * 100}%"],
["频繁项集总数量", sum(len(v) for v in frequent_itemsets.values())],
["强关联规则数量", len(strong_rules)]
]
print(format_table(["指标", "数值"], data_overview, align="center"))
print_separator(title="二、频繁项集详情")
if not frequent_itemsets:
print("⚠️ 未挖掘到满足最小支持度的频繁项集,请降低最小支持度阈值!")
else:
for k in sorted(frequent_itemsets.keys()):
fk_items = frequent_itemsets[k]
rows = [[",".join(itemset), support] for itemset, support in fk_items]
print(f"\n【{k}-项集(共{len(fk_items)}个)】")
print(format_table([f"{k}-项集", "支持度"], rows, align="left"))
fk_count = {f"{k}-项集": len(v) for k, v in frequent_itemsets.items()}
print("\n" + text_bar_chart(fk_count, "频繁项集数量分布", "数量", "项集维度"))
print_separator(title="三、强关联规则详情(按提升度降序)")
if not strong_rules:
print("⚠️ 未生成满足最小置信度的强关联规则,请降低最小置信度/支持度阈值!")
else:
rows = []
for S, Y, sup, conf, lift in strong_rules:
rel_type = "强正关联" if lift > 1.2 else "弱正关联" if lift > 1 else "无关联/负关联"
rows.append([",".join(S) + " → " + ",".join(Y), sup, conf, lift, rel_type])
print(format_table(["关联规则", "支持度", "置信度", "提升度", "关联类型"], rows, align="left"))
lift_count = defaultdict(int)
for _, _, _, _, lift in strong_rules:
if lift > 1.2:
lift_count["lift>1.2(强正)"] += 1
elif lift > 1:
lift_count["1<lift≤1.2(弱正)"] += 1
else:
lift_count["lift≤1(无/负)"] += 1
print("\n" + text_bar_chart(lift_count, "强关联规则提升度分布", "数量", "提升度区间"))
print_separator(char="=", length=100)
# ===================== Matplotlib可视化模块 =====================
def plot_frequent_itemsets_count(frequent_itemsets, save_path="./"):
"""图1:频繁项集按维度分布的柱状图"""
if not frequent_itemsets:
print("⚠️ 无频繁项集,跳过【频繁项集数量分布】绘图")
return
k_list = sorted(frequent_itemsets.keys())
count_list = [len(frequent_itemsets[k]) for k in k_list]
x_labels = [f"{k}-项集" for k in k_list]
fig, ax = plt.subplots(figsize=(8, 5))
bars = ax.bar(x_labels, count_list, color=COLORS[:len(k_list)], edgecolor="black", alpha=0.8)
for bar, count in zip(bars, count_list):
ax.text(bar.get_x() + bar.get_width() / 2, bar.get_height() + 0.1, str(count), ha="center", va="bottom",
fontweight="bold")
ax.set_title("频繁项集数量按维度分布", fontsize=14, fontweight="bold", pad=20)
ax.set_xlabel("项集维度", fontsize=12, labelpad=10)
ax.set_ylabel("频繁项集数量", fontsize=12, labelpad=10)
ax.grid(axis="y", linestyle="--")
ax.set_ylim(0, max(count_list) * 1.2)
fig.tight_layout()
save_file = os.path.join(save_path, "1-频繁项集数量分布.png")
plt.savefig(save_file, bbox_inches="tight")
print(f"✅ 【频繁项集数量分布】图已保存至:{save_file}")
def plot_frequent_itemsets_support(frequent_itemsets, save_path="./"):
"""图2:各维度频繁项集支持度条形图(子图版)"""
if not frequent_itemsets:
print("⚠️ 无频繁项集,跳过【频繁项集支持度】绘图")
return
k_sorted = sorted(frequent_itemsets.keys())
n_cols = 2 if len(k_sorted) >= 2 else 1
n_rows = (len(k_sorted) + n_cols - 1) // n_cols
fig, axes = plt.subplots(n_rows, n_cols, figsize=(6 * n_cols, 5 * n_rows), squeeze=False)
axes = axes.flatten()
for idx, k in enumerate(k_sorted):
ax = axes[idx]
fk_items = frequent_itemsets[k]
itemset_str = [",".join(itemset) for itemset, sup in fk_items]
support_list = [sup for itemset, sup in fk_items]
bars = ax.barh(itemset_str, support_list, color=COLORS[0], edgecolor="black", alpha=0.8)
for bar, sup in zip(bars, support_list):
ax.text(bar.get_width() + 0.01, bar.get_y() + bar.get_height() / 2, f"{sup:.4f}", ha="left", va="center",
fontweight="bold")
ax.set_title(f"{k}-项集 支持度分布", fontsize=12, fontweight="bold", pad=15)
ax.set_xlabel("支持度", fontsize=10, labelpad=5)
ax.set_xlim(0, 1.05)
ax.grid(axis="x", linestyle="--")
for idx in range(len(k_sorted), len(axes)):
axes[idx].set_visible(False)
fig.suptitle("各维度频繁项集支持度详情", fontsize=14, fontweight="bold", y=1.02)
fig.tight_layout()
save_file = os.path.join(save_path, "2-频繁项集支持度分布.png")
plt.savefig(save_file, bbox_inches="tight")
print(f"✅ 【频繁项集支持度分布】图已保存至:{save_file}")
def plot_association_rules_scatter(strong_rules, save_path="./"):
"""图3:关联规则 支持度-置信度 散点图(基础版)"""
if not strong_rules:
print("⚠️ 无强关联规则,跳过【关联规则散点图】绘图")
return
support_list, confidence_list, lift_list, rel_type_list = [], [], [], []
for S, Y, sup, conf, lift in strong_rules:
support_list.append(sup)
confidence_list.append(conf)
lift_list.append(lift)
rel_type_list.append("强正关联" if lift > 1.2 else "弱正关联" if lift > 1 else "无关联/负关联")
lift_norm = [(lift - min(lift_list)) / (max(lift_list) - min(lift_list)) * 500 + 100 for lift in lift_list]
fig, ax = plt.subplots(figsize=(10, 6))
for rel_type in ["强正关联", "弱正关联", "无关联/负关联"]:
if rel_type not in rel_type_list:
continue
mask = [r == rel_type for r in rel_type_list]
ax.scatter(
[s for s, m in zip(support_list, mask) if m],
[c for c, m in zip(confidence_list, mask) if m],
s=[l for l, m in zip(lift_norm, mask) if m],
c=REL_COLORS[rel_type], label=rel_type, alpha=0.7, edgecolors="black", linewidth=0.5
)
ax.set_title("关联规则:支持度 × 置信度(点大小=提升度)", fontsize=14, fontweight="bold", pad=20)
ax.set_xlabel("支持度", fontsize=12, labelpad=10)
ax.set_ylabel("置信度", fontsize=12, labelpad=10)
ax.legend(loc="best", frameon=True, shadow=True)
ax.grid(True, linestyle="--", alpha=0.5)
ax.set_xlim(0, 1.05)
ax.set_ylim(0, 1.05)
fig.tight_layout()
save_file = os.path.join(save_path, "3-关联规则_支持度-置信度散点图.png")
plt.savefig(save_file, bbox_inches="tight")
print(f"✅ 【关联规则散点图】已保存至:{save_file}")
def plot_lift_distribution(strong_rules, save_path="./"):
"""图4:提升度区间分布(柱状图+饼图 双图)"""
if not strong_rules:
print("⚠️ 无强关联规则,跳过【提升度分布】绘图")
return
lift_count = defaultdict(int)
for _, _, _, _, lift in strong_rules:
if lift > 1.2:
lift_count["lift>1.2\n(强正关联)"] += 1
elif lift > 1:
lift_count["1<lift≤1.2\n(弱正关联)"] += 1
else:
lift_count["lift≤1\n(无/负关联)"] += 1
labels, values = list(lift_count.keys()), list(lift_count.values())
colors = [REL_COLORS["强正关联"], REL_COLORS["弱正关联"], REL_COLORS["无关联/负关联"]][:len(labels)]
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
bars = ax1.bar(labels, values, color=colors, edgecolor="black", alpha=0.8)
for bar, val in zip(bars, values):
ax1.text(bar.get_x() + bar.get_width() / 2, bar.get_height() + 0.1, str(val), ha="center", va="bottom",
fontweight="bold")
ax1.set_title("提升度区间 规则数量", fontsize=12, fontweight="bold", pad=15)
ax1.set_ylabel("规则数量", fontsize=10, labelpad=10)
ax1.grid(axis="y", linestyle="--")
ax1.set_ylim(0, max(values) * 1.2)
ax2.set_title("提升度区间 规则占比", fontsize=12, fontweight="bold", pad=15)
wedges, texts, autotexts = ax2.pie(
values, labels=labels, colors=colors, autopct="%1.1f%%",
startangle=90, wedgeprops={"edgecolor": "black", "linewidth": 1}
)
for autotext in autotexts:
autotext.set_color("white")
autotext.set_fontweight("bold")
fig.suptitle("关联规则提升度区间分布", fontsize=14, fontweight="bold", y=1.02)
fig.tight_layout()
save_file = os.path.join(save_path, "4-关联规则提升度区间分布.png")
plt.savefig(save_file, bbox_inches="tight")
print(f"✅ 【关联规则提升度分布】图已保存至:{save_file}")
# ---------------------- 核心规则标签散点图 ----------------------
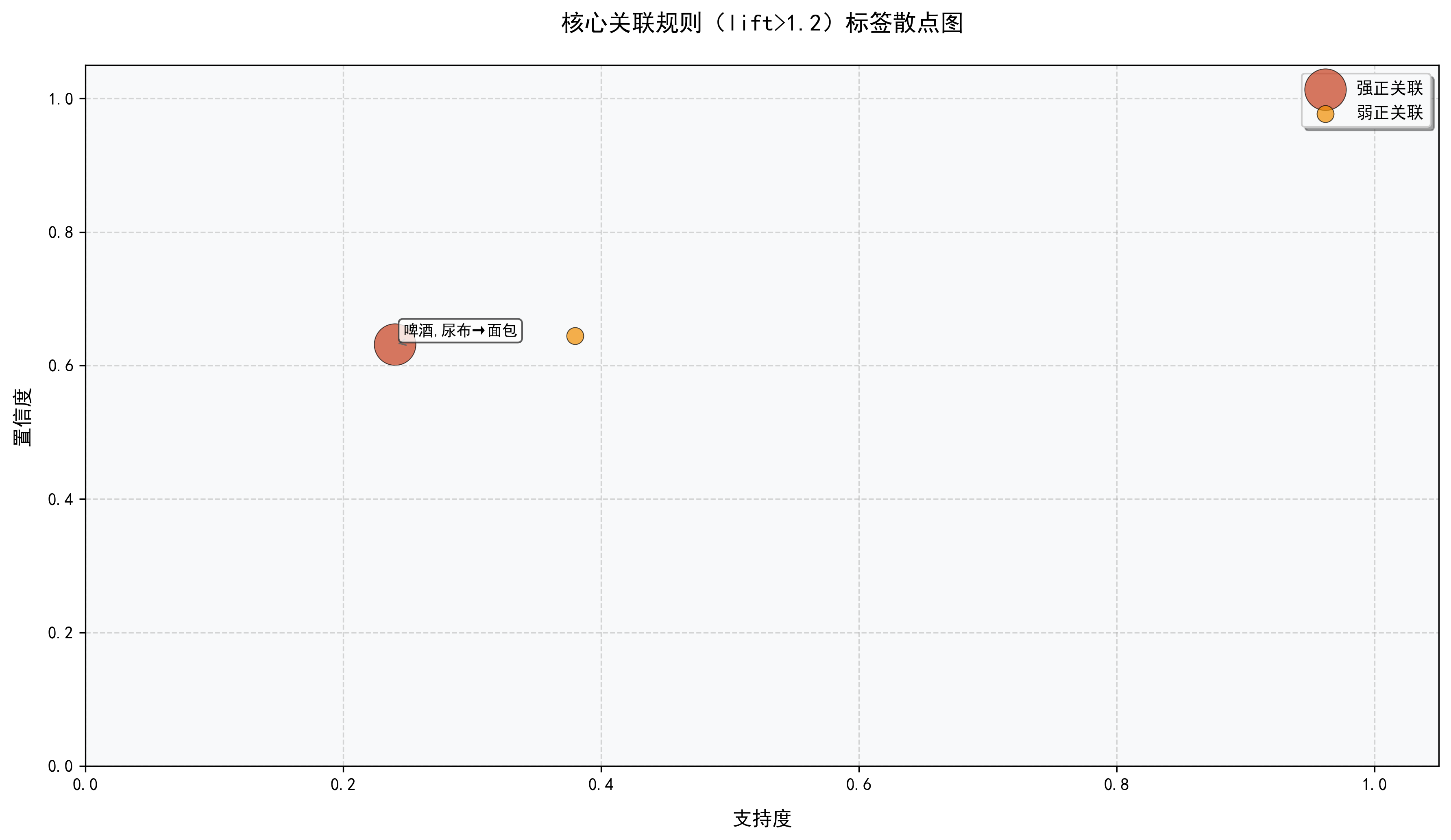
def plot_core_rules_label_scatter(strong_rules, save_path="./"):
"""图5:核心关联规则标签散点图(lift>1.2,添加文字标签)"""
if not strong_rules:
print("⚠️ 无强关联规则,跳过【核心规则标签散点图】绘图")
return
# 筛选核心规则(lift>1.2)+ 所有规则基础数据
support_list, confidence_list, lift_list, rel_type_list, rule_str_list = [], [], [], [], []
core_rule_mask = [] # 标记是否为核心规则
for S, Y, sup, conf, lift in strong_rules:
support_list.append(sup)
confidence_list.append(conf)
lift_list.append(lift)
rel_type = "强正关联" if lift > 1.2 else "弱正关联" if lift > 1 else "无关联/负关联"
rel_type_list.append(rel_type)
rule_str_list.append(f"{','.join(S)}→{','.join(Y)}")
core_rule_mask.append(lift > 1.2)
# 无核心规则则跳过
if not any(core_rule_mask):
print("⚠️ 无核心规则(lift>1.2),跳过【核心规则标签散点图】绘图")
return
# 归一化提升度(点大小)
lift_norm = [(lift - min(lift_list)) / (max(lift_list) - min(lift_list)) * 500 + 100 for lift in lift_list]
fig, ax = plt.subplots(figsize=(12, 7))
# 绘制所有规则散点
for rel_type in ["强正关联", "弱正关联", "无关联/负关联"]:
if rel_type not in rel_type_list:
continue
mask = [r == rel_type for r in rel_type_list]
ax.scatter(
[s for s, m in zip(support_list, mask) if m],
[c for c, m in zip(confidence_list, mask) if m],
s=[l for l, m in zip(lift_norm, mask) if m],
c=REL_COLORS[rel_type], label=rel_type, alpha=0.7, edgecolors="black", linewidth=0.5
)
# 为核心规则添加文字标签(避免重叠,轻微偏移)
for i, is_core in enumerate(core_rule_mask):
if is_core:
ax.annotate(
rule_str_list[i], # 规则标签
xy=(support_list[i], confidence_list[i]), # 标签对应点
xytext=(5, 5), # 标签偏移量
textcoords="offset points",
fontsize=9,
bbox=dict(boxstyle="round,pad=0.3", facecolor="white", alpha=0.8, edgecolor="#333333"),
arrowprops=dict(arrowstyle="->", color="#666666", lw=0.8)
)
# 样式设置
ax.set_title("核心关联规则(lift>1.2)标签散点图", fontsize=14, fontweight="bold", pad=20)
ax.set_xlabel("支持度", fontsize=12, labelpad=10)
ax.set_ylabel("置信度", fontsize=12, labelpad=10)
ax.legend(loc="best", frameon=True, shadow=True)
ax.grid(True, linestyle="--", alpha=0.5)
ax.set_xlim(0, 1.05)
ax.set_ylim(0, 1.05)
fig.tight_layout()
save_file = os.path.join(save_path, "5-核心关联规则标签散点图.png")
plt.savefig(save_file, bbox_inches="tight")
print(f"✅ 【核心关联规则标签散点图】已保存至:{save_file}")
# ---------------------- 3-项集及以上支持度热力图 ----------------------
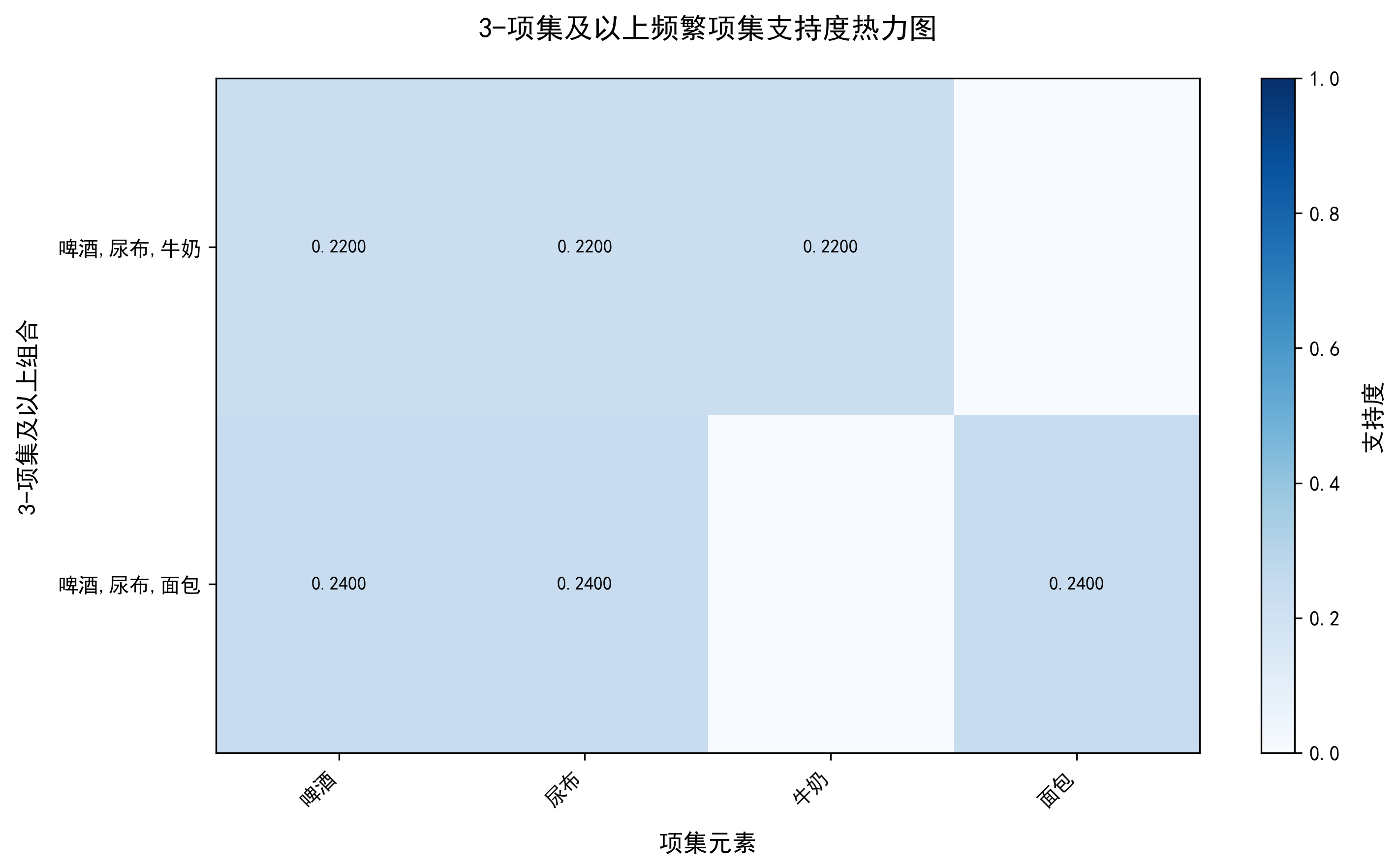
def plot_3itemset_support_heatmap(frequent_itemsets, save_path="./"):
"""图6:3-项集及以上频繁项集支持度热力图"""
if not frequent_itemsets:
print("⚠️ 无频繁项集,跳过【3-项集支持度热力图】绘图")
return
# 筛选3-项集及以上
high_k_items = []
for k in frequent_itemsets:
if k >= 3:
high_k_items.extend(frequent_itemsets[k])
if not high_k_items:
print("⚠️ 无3-项集及以上频繁项集,跳过【3-项集支持度热力图】绘图")
return
# 处理数据:提取所有唯一元素,构建项集-元素矩阵
all_items = sorted(list(set(item for itemset, _ in high_k_items for item in itemset)))
itemset_str = [",".join(sorted(itemset)) for itemset, sup in high_k_items]
support_vals = [sup for itemset, sup in high_k_items]
# 构建热力图数据矩阵
heatmap_data = np.zeros((len(itemset_str), len(all_items)))
for i, (itemset, sup) in enumerate(high_k_items):
for j, item in enumerate(all_items):
if item in itemset:
heatmap_data[i, j] = sup
# 绘图
fig, ax = plt.subplots(figsize=(10, max(6, len(itemset_str) * 0.8)))
im = ax.imshow(heatmap_data, cmap="Blues", aspect="auto", vmin=0, vmax=1)
# 设置坐标轴标签
ax.set_xticks(range(len(all_items)))
ax.set_xticklabels(all_items, rotation=45, ha="right")
ax.set_yticks(range(len(itemset_str)))
ax.set_yticklabels(itemset_str)
# 添加数值标签
for i in range(len(itemset_str)):
for j in range(len(all_items)):
if heatmap_data[i, j] > 0:
text = ax.text(j, i, f"{heatmap_data[i, j]:.4f}",
ha="center", va="center", color="black" if heatmap_data[i, j] < 0.5 else "white",
fontweight="bold", fontsize=9)
# 颜色条
cbar = fig.colorbar(im, ax=ax)
cbar.set_label("支持度", fontsize=12, labelpad=10)
# 样式设置
ax.set_title("3-项集及以上频繁项集支持度热力图", fontsize=14, fontweight="bold", pad=20)
ax.set_xlabel("项集元素", fontsize=12, labelpad=10)
ax.set_ylabel("3-项集及以上组合", fontsize=12, labelpad=10)
fig.tight_layout()
save_file = os.path.join(save_path, "6-3项集及以上支持度热力图.png")
plt.savefig(save_file, bbox_inches="tight")
print(f"✅ 【3-项集支持度热力图】已保存至:{save_file}")
# ---------------------- 规则置信度分布直方图 ----------------------
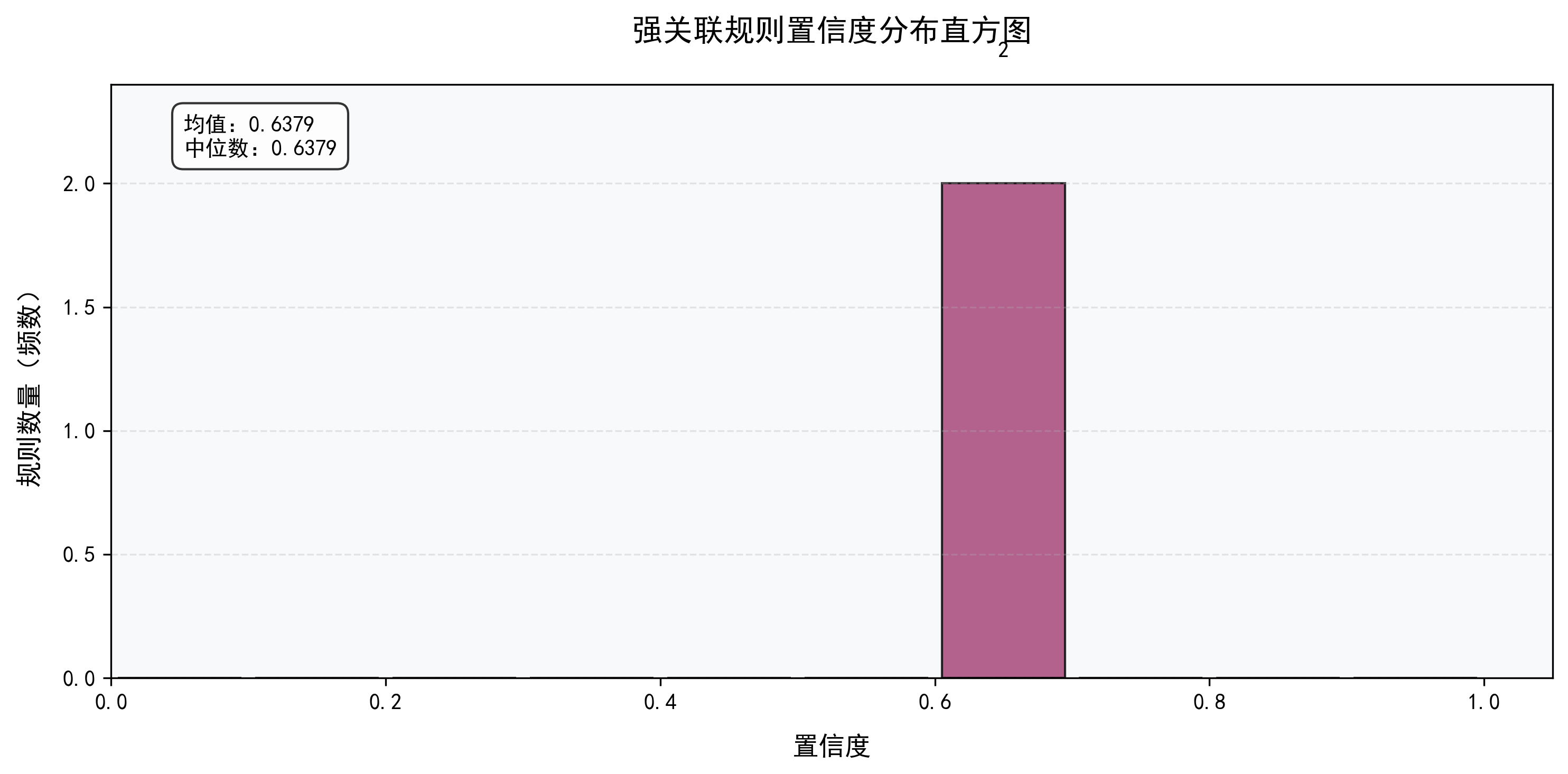
def plot_confidence_distribution(strong_rules, save_path="./"):
"""图7:强关联规则置信度分布直方图"""
if not strong_rules:
print("⚠️ 无强关联规则,跳过【置信度分布直方图】绘图")
return
# 提取置信度数据
confidence_vals = [conf for _, _, _, conf, _ in strong_rules]
# 绘图:自动分箱(10个区间,适配0-1范围)
fig, ax = plt.subplots(figsize=(10, 5))
n, bins, patches = ax.hist(confidence_vals, bins=10, range=(0, 1), color=COLORS[1],
edgecolor="black", alpha=0.8, rwidth=0.9)
# 添加频数标签
for patch, count in zip(patches, n):
if count > 0:
ax.text(patch.get_x() + patch.get_width() / 2, patch.get_height() + 0.5,
str(int(count)), ha="center", va="bottom", fontweight="bold")
# 样式设置
ax.set_title("强关联规则置信度分布直方图", fontsize=14, fontweight="bold", pad=20)
ax.set_xlabel("置信度", fontsize=12, labelpad=10)
ax.set_ylabel("规则数量(频数)", fontsize=12, labelpad=10)
ax.grid(axis="y", linestyle="--")
ax.set_xlim(0, 1.05)
ax.set_ylim(0, max(n) * 1.2)
# 添加统计信息
mean_conf = np.mean(confidence_vals)
median_conf = np.median(confidence_vals)
ax.text(0.05, 0.95, f"均值:{mean_conf:.4f}\n中位数:{median_conf:.4f}",
transform=ax.transAxes, ha="left", va="top",
bbox=dict(boxstyle="round,pad=0.5", facecolor="white", alpha=0.8))
fig.tight_layout()
save_file = os.path.join(save_path, "7-关联规则置信度分布直方图.png")
plt.savefig(save_file, bbox_inches="tight")
print(f"✅ 【置信度分布直方图】已保存至:{save_file}")
# ---------------------- 3D支持度-置信度-提升度散点图 ----------------------
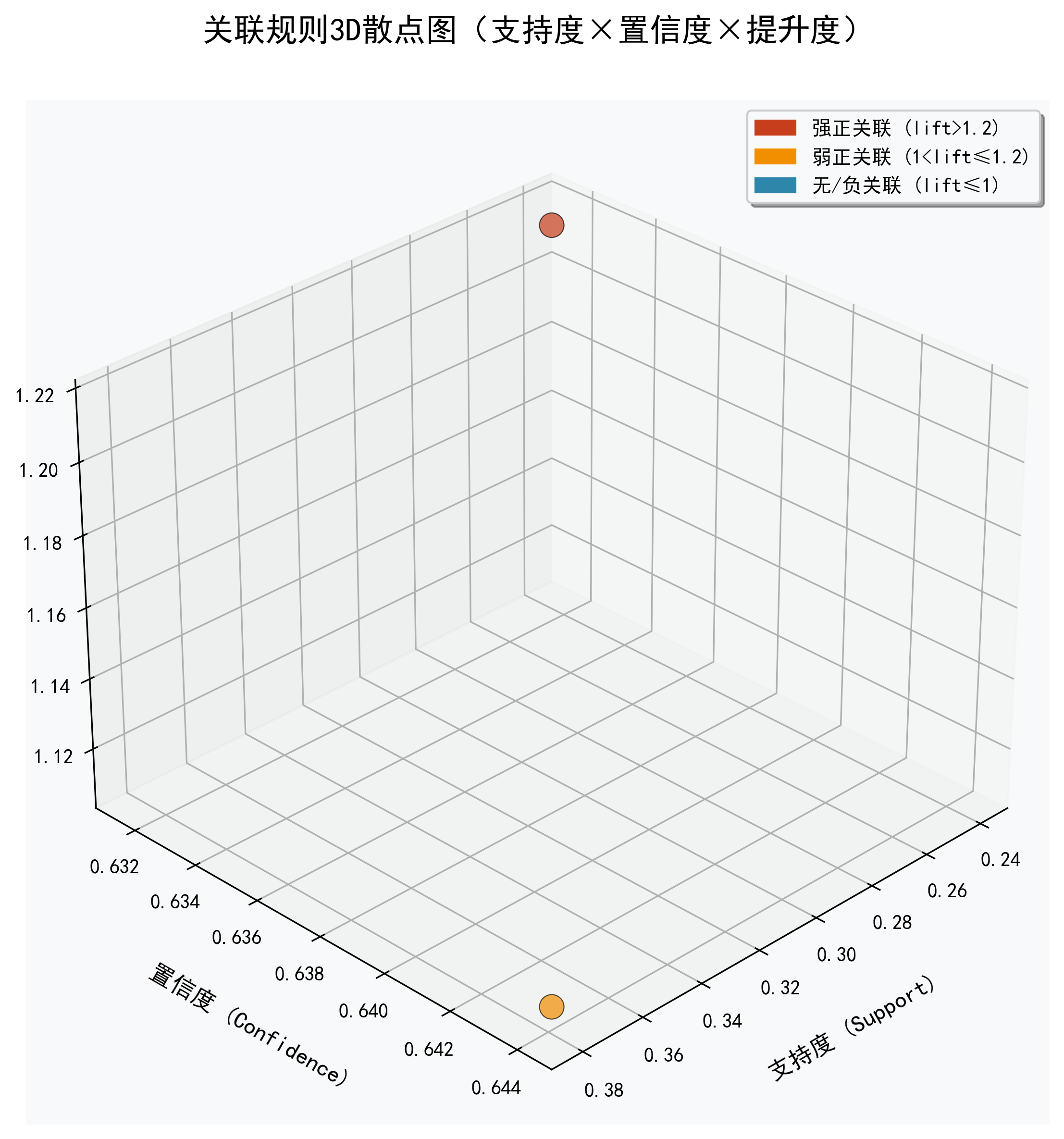
def plot_3d_rule_scatter(strong_rules, save_path="./"):
"""图8:3D散点图(x=支持度,y=置信度,z=提升度)"""
if not strong_rules:
print("⚠️ 无强关联规则,跳过【3D规则散点图】绘图")
return
# 提取数据并分类
support_list, confidence_list, lift_list, color_list = [], [], [], []
for S, Y, sup, conf, lift in strong_rules:
support_list.append(sup)
confidence_list.append(conf)
lift_list.append(lift)
# 按关联类型配色
if lift > 1.2:
color_list.append(REL_COLORS["强正关联"])
elif lift > 1:
color_list.append(REL_COLORS["弱正关联"])
else:
color_list.append(REL_COLORS["无关联/负关联"])
# 创建3D画布
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
# 绘制3D散点
scatter = ax.scatter(support_list, confidence_list, lift_list,
c=color_list, s=150, alpha=0.7, edgecolors="black", linewidth=0.5)
# 设置坐标轴标签
ax.set_xlabel("支持度 (Support)", fontsize=12, labelpad=15)
ax.set_ylabel("置信度 (Confidence)", fontsize=12, labelpad=15)
ax.set_zlabel("提升度 (Lift)", fontsize=12, labelpad=15)
# 设置视角(仰角30°,方位角45°,可手动旋转)
ax.view_init(elev=30, azim=45)
# 添加图例
legend_elements = [mpatches.Patch(color=REL_COLORS["强正关联"], label="强正关联 (lift>1.2)"),
mpatches.Patch(color=REL_COLORS["弱正关联"], label="弱正关联 (1<lift≤1.2)"),
mpatches.Patch(color=REL_COLORS["无关联/负关联"], label="无/负关联 (lift≤1)")]
ax.legend(handles=legend_elements, loc="best", frameon=True, shadow=True)
# 样式设置
ax.set_title("关联规则3D散点图(支持度×置信度×提升度)", fontsize=16, fontweight="bold", pad=30)
ax.grid(True, alpha=0.3)
# 保存
fig.tight_layout()
save_file = os.path.join(save_path, "8-关联规则3D散点图.png")
plt.savefig(save_file, bbox_inches="tight")
print(f"✅ 【3D规则散点图】已保存至:{save_file}")
# ===================== 可视化总入口(整合原有+新增)=====================
def matplot_visualize_all(transaction_set, frequent_itemsets, strong_rules, total_trans, save_path="./"):
"""Matplotlib可视化总入口:一键生成所有8类图表"""
print_separator(char="*", title="开始生成Matplotlib可视化图表(共8类)", length=80)
if not os.path.exists(save_path):
os.makedirs(save_path)
# 8类图表
plot_frequent_itemsets_count(frequent_itemsets, save_path)
plot_frequent_itemsets_support(frequent_itemsets, save_path)
plot_association_rules_scatter(strong_rules, save_path)
plot_lift_distribution(strong_rules, save_path)
plot_core_rules_label_scatter(strong_rules, save_path)
plot_3itemset_support_heatmap(frequent_itemsets, save_path)
plot_confidence_distribution(strong_rules, save_path)
plot_3d_rule_scatter(strong_rules, save_path)
# 显示所有图表
plt.show()
print_separator(char="*", title="Matplotlib可视化图表(8类)生成完成", length=80)
# ===================== 报告生成模块 =====================
def generate_visual_report(transaction_set, frequent_itemsets, strong_rules, total_trans,
report_path="apriori_analysis_report.txt"):
"""生成纯文本可视化报告文件(保存到本地)"""
with open(report_path, "w", encoding="utf-8") as f:
original_stdout = sys.stdout
sys.stdout = f
visualize_analysis_result(transaction_set, frequent_itemsets, strong_rules, total_trans)
sys.stdout = original_stdout
print_separator(title=f"纯文本报告已保存到本地文件", length=80)
print(f"报告文件路径:{os.path.abspath(report_path)}")
# ===================== 主函数(交互入口)=====================
def main():
"""主函数:交互式执行Apriori算法全流程"""
print("=" * 80)
print(" Apriori算法(无第三方库) ")
print("=" * 80)
# 第一步:选择数据来源
while True:
data_choice = input("\n请选择数据来源【1-内置测试数据(购物篮)/2-本地TXT文件】:").strip()
if data_choice in ["1", "2"]:
break
print("输入无效,请输入1或2!")
if data_choice == "2":
file_path = input("请输入本地TXT事务文件路径(每行一个事务,项用逗号/空格分隔):").strip()
try:
transactions, _ = load_transactions(data_source="file", file_path=file_path)
except Exception as e:
print(f"文件加载失败:{e},自动切换到内置测试数据!")
transactions, _ = load_transactions(data_source="test")
else:
transactions, _ = load_transactions(data_source="test")
# 第二步:设置算法阈值
print("\n请设置算法阈值(建议:支持度0.2-0.6,置信度0.6-0.9)")
while True:
try:
min_support = float(input("最小支持度阈值(0-1):").strip())
if 0 < min_support < 1:
break
print("最小支持度必须是0-1之间的正数!")
except ValueError:
print("输入无效,请输入数字(如0.4)!")
while True:
try:
min_confidence = float(input("最小置信度阈值(0-1):").strip())
if 0 < min_confidence < 1:
break
print("最小置信度必须是0-1之间的正数!")
except ValueError:
print("输入无效,请输入数字(如0.8)!")
# 第三步:挖掘频繁项集
print_separator(char="*", title="开始挖掘频繁项集", length=80)
frequent_itemsets, total_trans = get_frequent_itemsets(transactions, min_support)
if not frequent_itemsets:
print("❌ 未挖掘到任何频繁项集,程序结束!")
return
# 第四步:生成关联规则
print_separator(char="*", title="开始生成关联规则", length=80)
strong_rules = generate_association_rules(frequent_itemsets, transactions, total_trans, min_confidence)
# 第五步:纯文本可视化+生成报告+8类Matplotlib可视化
visualize_analysis_result(transactions, frequent_itemsets, strong_rules, total_trans)
generate_visual_report(transactions, frequent_itemsets, strong_rules, total_trans)
matplot_visualize_all(transactions, frequent_itemsets, strong_rules, total_trans)
print("\n🎉 Apriori算法全流程执行完成!生成1个纯文本报告+8类高清可视化图表!")
if __name__ == "__main__":
# 解决Windows命令行中文显示问题
if os.name == "nt":
os.system("chcp 65001 > nul")
main()================================================================================
Apriori算法(无第三方库)
================================================================================
请选择数据来源【1-内置测试数据(购物篮)/2-本地TXT文件】:2
请输入本地TXT事务文件路径(每行一个事务,项用逗号/空格分隔):C:\Users\ABC\PycharmProjects\PythonProject47\apriori_random_transactions.txt
-------------------- 加载本地文件:apriori_random_transactions.txt --------------------
原始事务数:100 | 清洗后有效事务数:100
数据集中唯一项总数:10 | 所有项:['可乐', '啤酒', '尿布', '火腿肠', '牛奶', '矿泉水', '薯片', '酸奶', '面包', '鸡蛋']
请设置算法阈值(建议:支持度0.2-0.6,置信度0.6-0.9)
最小支持度阈值(0-1):0.2
最小置信度阈值(0-1):0.6
*********************************** 开始挖掘频繁项集 ***********************************
--------------------------------- 挖掘到10个1-频繁项集 ---------------------------------
--------------------------------- 挖掘到10个2-频繁项集 ---------------------------------
--------------------------------- 挖掘到2个3-频繁项集 ---------------------------------
*********************************** 开始生成关联规则 ***********************************
======================================== Apriori算法分析结果可视化报告 ========================================
----------------------------------- 一、数据基本概览 -----------------------------------
指标 | 数值
------- | -----
总事务数 | 100
有效事务数 | 100
唯一项总数 | 10
数据稀疏度 | 57.4%
频繁项集总数量 | 22
强关联规则数量 | 2
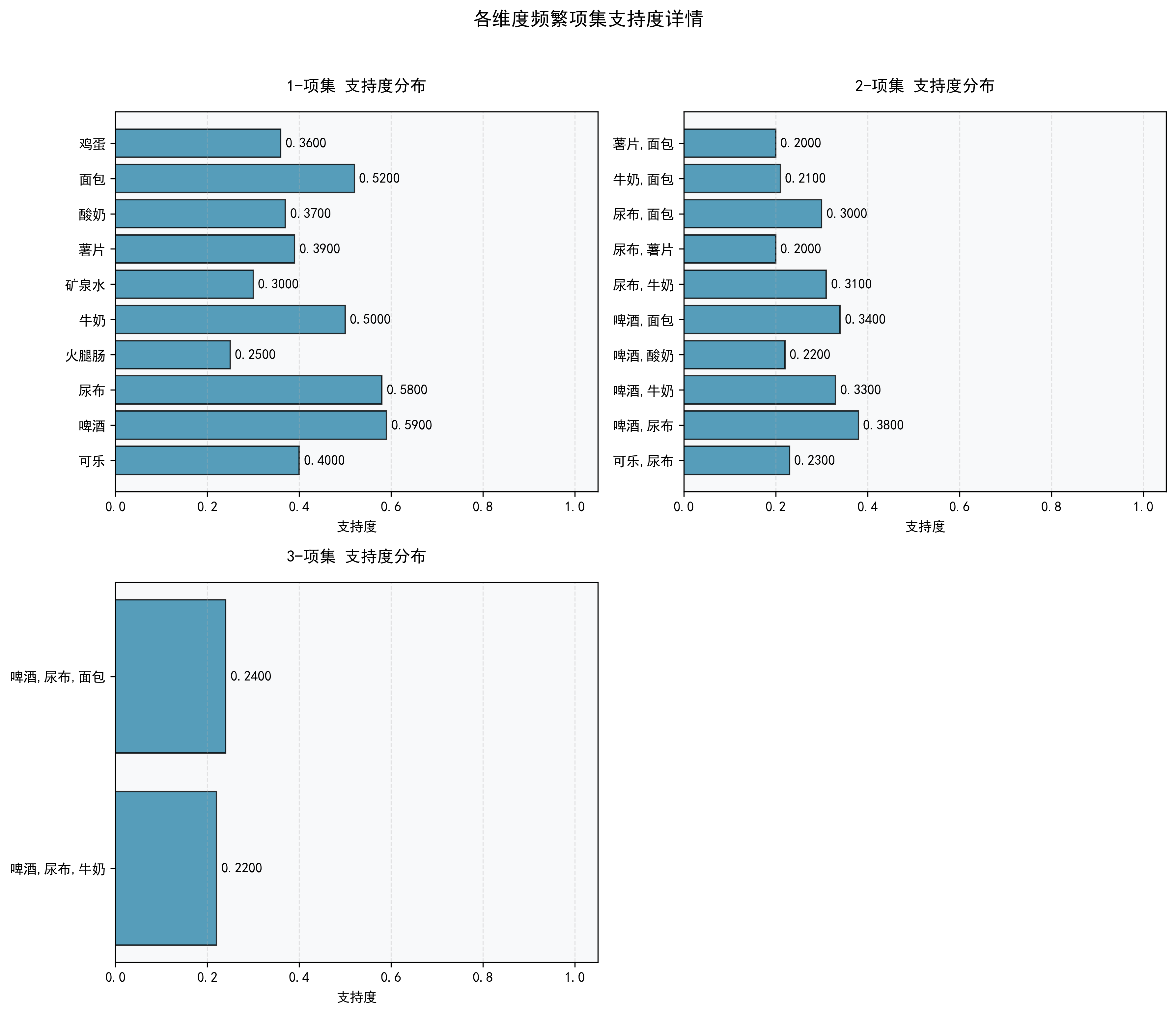
----------------------------------- 二、频繁项集详情 -----------------------------------
【1-项集(共10个)】
1-项集 | 支持度
---- | ----
可乐 | 0.4
啤酒 | 0.59
尿布 | 0.58
火腿肠 | 0.25
牛奶 | 0.5
矿泉水 | 0.3
薯片 | 0.39
酸奶 | 0.37
面包 | 0.52
鸡蛋 | 0.36
【2-项集(共10个)】
2-项集 | 支持度
----- | ----
可乐,尿布 | 0.23
啤酒,尿布 | 0.38
啤酒,牛奶 | 0.33
啤酒,酸奶 | 0.22
啤酒,面包 | 0.34
尿布,牛奶 | 0.31
尿布,薯片 | 0.2
尿布,面包 | 0.3
牛奶,面包 | 0.21
薯片,面包 | 0.2
【3-项集(共2个)】
3-项集 | 支持度
-------- | ----
啤酒,尿布,牛奶 | 0.22
啤酒,尿布,面包 | 0.24
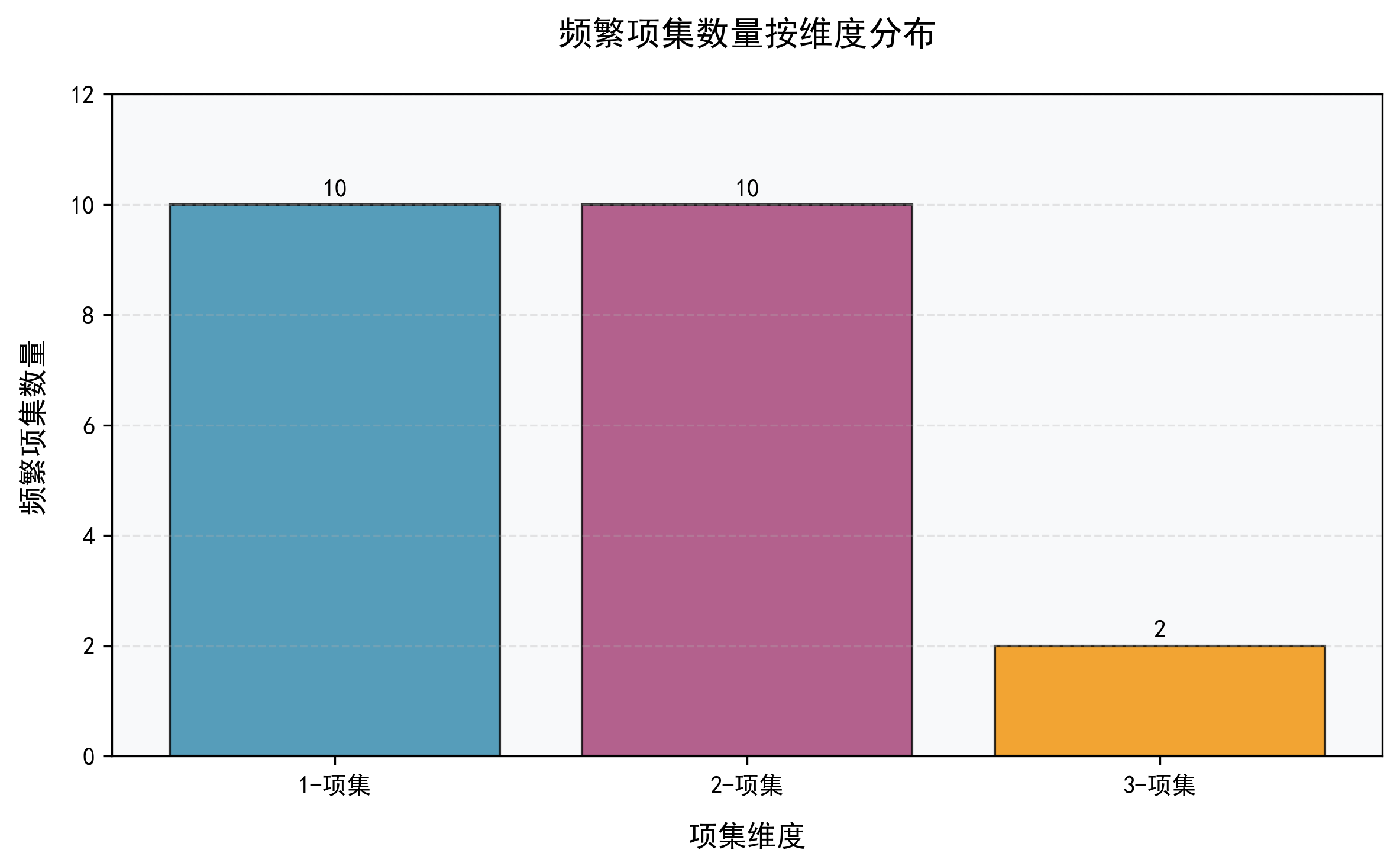
【频繁项集数量分布】
项集维度 | 数量 (数值)
1-项集 | ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■ (10)
2-项集 | ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■ (10)
3-项集 | ■■■■■■■■■■ (2)
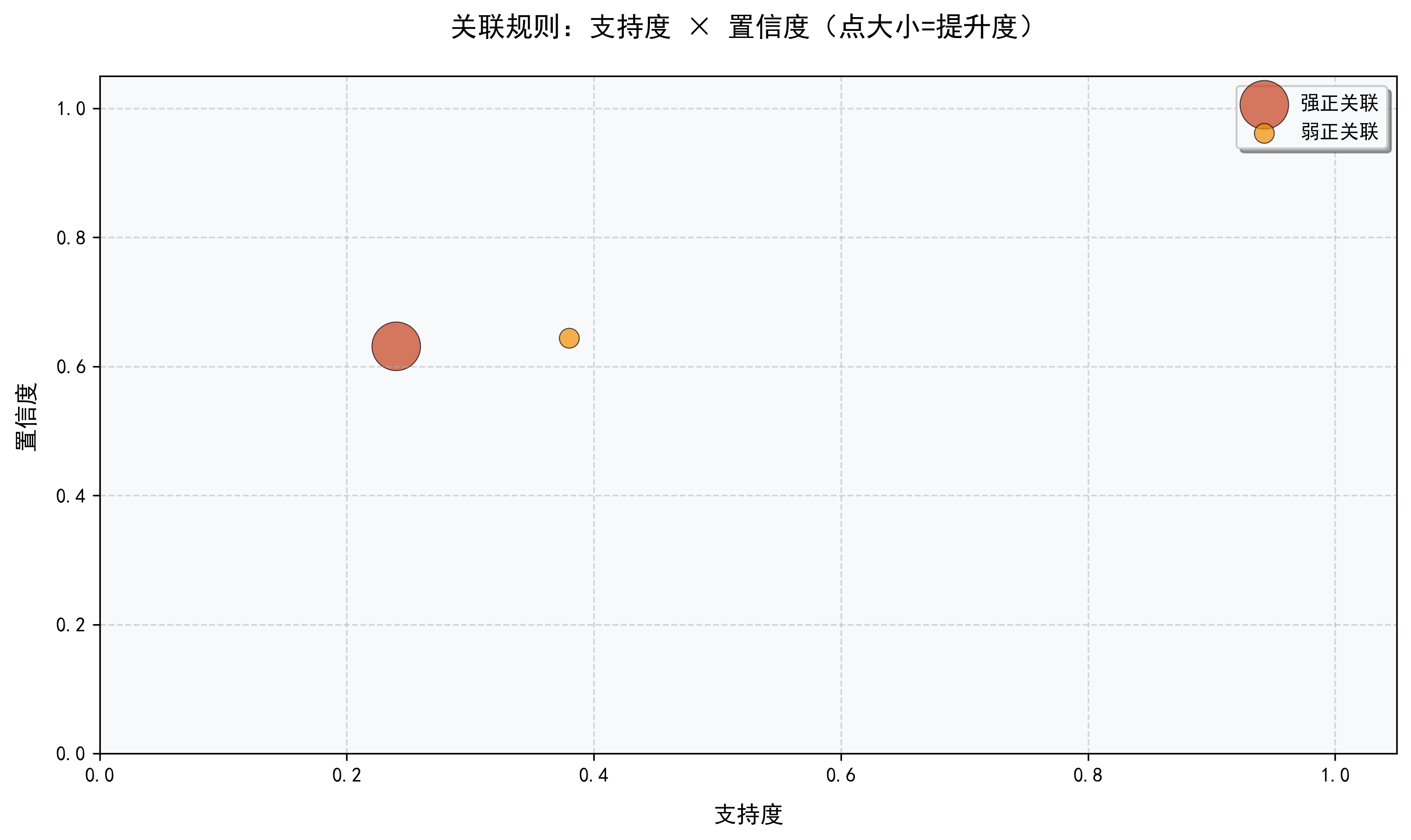
------------------------------ 三、强关联规则详情(按提升度降序) ------------------------------
关联规则 | 支持度 | 置信度 | 提升度 | 关联类型
---------- | ---- | ------ | ------ | ----
啤酒,尿布 → 面包 | 0.24 | 0.6316 | 1.2146 | 强正关联
啤酒 → 尿布 | 0.38 | 0.6441 | 1.1105 | 弱正关联
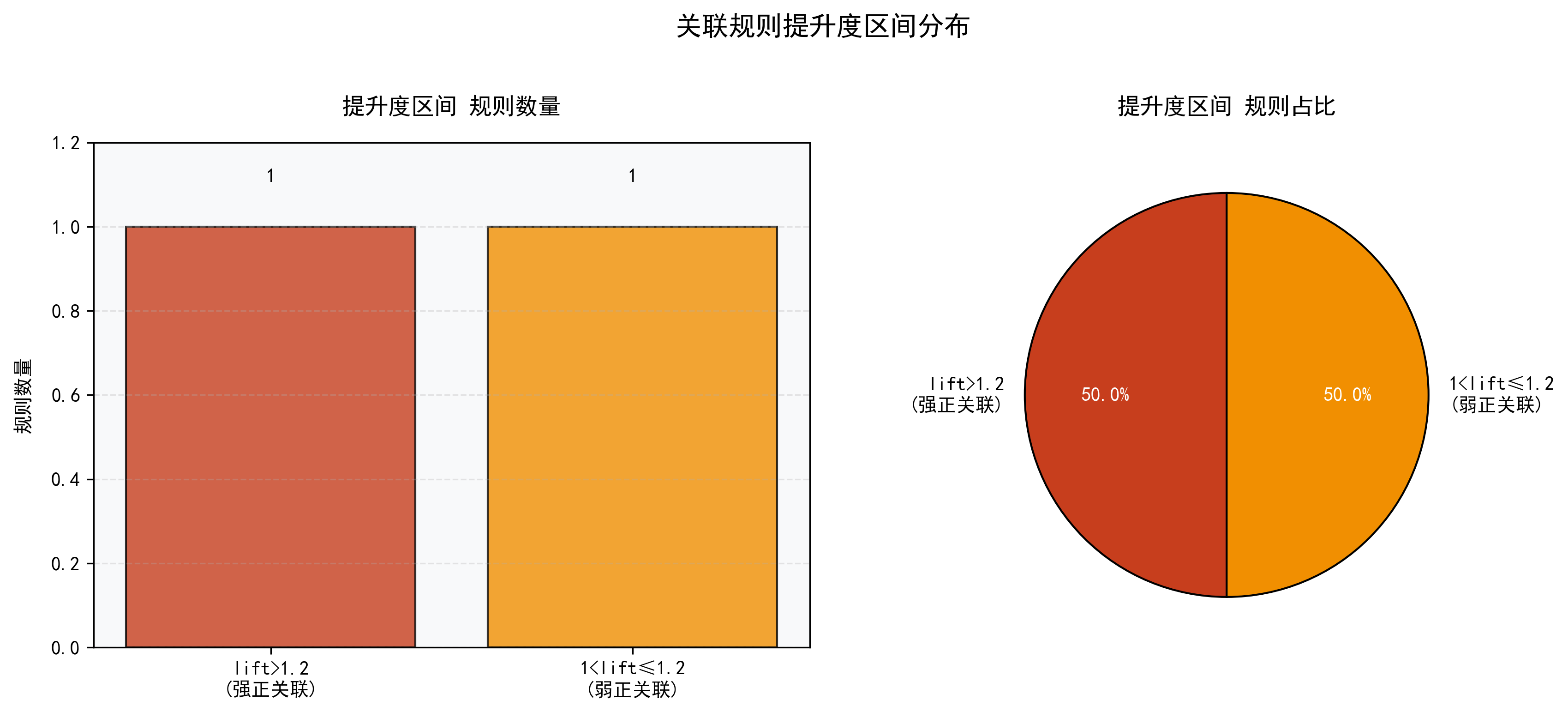
【强关联规则提升度分布】
提升度区间 | 数量 (数值)
lift>1.2(强正) | ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■ (1)
1<lift≤1.2(弱正) | ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■ (1)
====================================================================================================
-------------------------------- 纯文本报告已保存到本地文件 --------------------------------
报告文件路径:C:\Users\ABC\PycharmProjects\PythonProject47\apriori_analysis_report.txt
*************************** 开始生成Matplotlib可视化图表(共8类) ***************************
✅ 【频繁项集数量分布】图已保存至:./1-频繁项集数量分布.png
✅ 【频繁项集支持度分布】图已保存至:./2-频繁项集支持度分布.png
✅ 【关联规则散点图】已保存至:./3-关联规则_支持度-置信度散点图.png
✅ 【关联规则提升度分布】图已保存至:./4-关联规则提升度区间分布.png
✅ 【核心关联规则标签散点图】已保存至:./5-核心关联规则标签散点图.png
✅ 【3-项集支持度热力图】已保存至:./6-3项集及以上支持度热力图.png
✅ 【置信度分布直方图】已保存至:./7-关联规则置信度分布直方图.png
✅ 【3D规则散点图】已保存至:./8-关联规则3D散点图.png
*************************** Matplotlib可视化图表(8类)生成完成 ***************************
🎉 Apriori算法全流程执行完成!生成1个纯文本报告+8类高清可视化图表!
九、总结
Apriori算法是关联规则挖掘的经典算法,由Agrawal和Srikant于1994年提出。该算法通过逐层搜索和先验性质剪枝策略,从大规模数据集中发现频繁项集和关联规则。核心概念包括支持度、置信度和提升度等指标,算法流程分为频繁项集挖掘和规则生成两个阶段。虽然Apriori算法原理简单、结果可靠,但也存在计算效率低、内存消耗大等缺点。其改进算法包括FP-Growth和Eclat等。该算法广泛应用于零售、电商、医疗等领域,如经典的"啤酒与尿布"购物篮分析。Python实现展示了算法全过程,包括数据预处理、频繁项集挖掘和规则生成等步骤。