目录
解法二:利用单调性,使用"同向双指针"来优化(同向双指针也称为滑动窗口)
[解法一:暴力枚举 + 哈希表(判断字符是否重复出现),O(N^2)](#解法一:暴力枚举 + 哈希表(判断字符是否重复出现),O(N^2))
[解法二:利用规律,使用滑动窗口,时间:O(N)空间:O(1)](#解法二:利用规律,使用滑动窗口,时间:O(N)空间:O(1))
[3.最大连续1的个数 III](#3.最大连续1的个数 III)
1.长度最小的子数组
https://leetcode.cn/problems/minimum-size-subarray-sum/description/

理解题意
1.全是正整数
2.找和大于target的最短长度数组
题目示例

算法原理
解法一:暴力枚举所有子数组的和
考虑到枚举子数组(先定义左区间,再枚举右区间)的时间复杂度为O(N^2),在求和,此时,时间复杂度变为O(N^3)
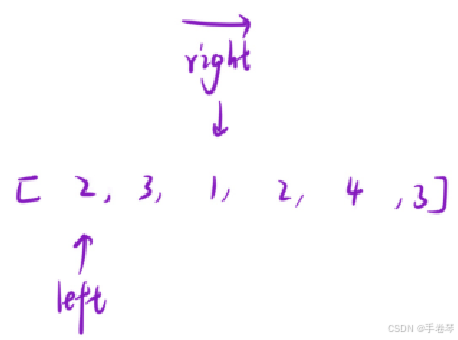
所以此时再优化一下:
解法二:利用单调性,使用"同向双指针"来优化(同向双指针也称为滑动窗口)
在上述两指针的前提下,再定义一个指针sum,用来统计以left为左区间的所有子数组的和
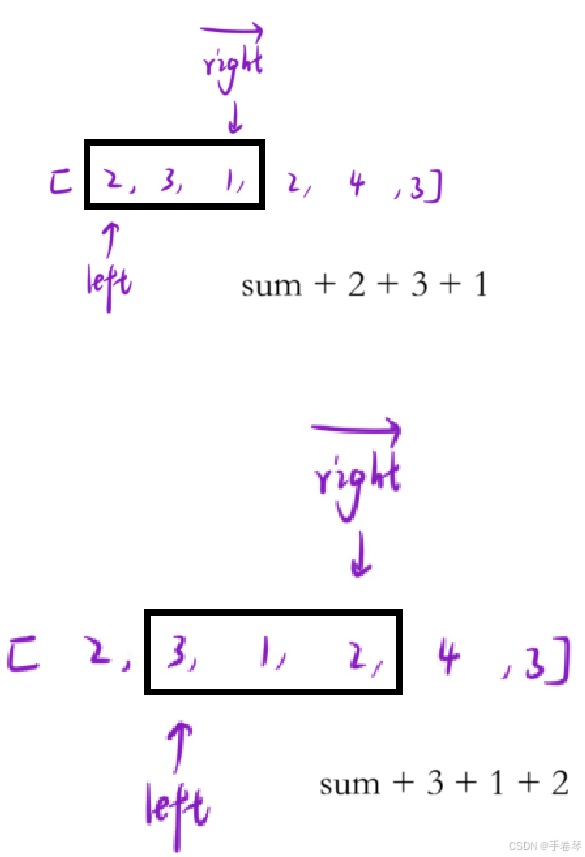
时间复杂度:看起来,进窗口和判断是两个套在一起的循环,时间复杂度为O(N^2),但实际操作中right和left每次只依次从左到右移动一位,实际时间复杂度为n + n -> 2n -> O(N)
本题做法
1.left = 0, right = 0
2.进窗口
3.判断
4.更新结果
5.出窗口
解法二利用单调性,规避了许多没有必要的枚举行为。
代码
class Solution
{
public:
int minSubArrayLen(int target, vector<int>& nums)
{
int n = nums.size(), sum = 0, len = INT_MAX;
// 因为len求最小值,如果len=0,那么最终只会返回0,所以直接定义它为最大值
for(int left = 0, right = 0; right < n; right++)
{
sum += nums[right]; // 进窗口
while(sum >= target) // 判断
{
len = min(len, right - left + 1); // 更新结果
sum -= nums[left++]; // 出窗口
}
}
return len == INT_MAX ? 0 : len;
}
};2.无重复字符的最长字串
https://leetcode.cn/problems/longest-substring-without-repeating-characters/description/

理解题意
字串的本质对应子数组,都是连续的一段
题目示例

算法原理
解法一:暴力枚举 + 哈希表(判断字符是否重复出现),O(N^2)
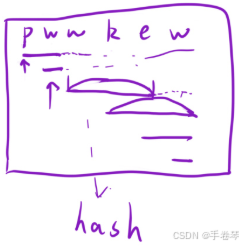
解法二:利用规律,使用滑动窗口,时间:O(N)空间:O(1)
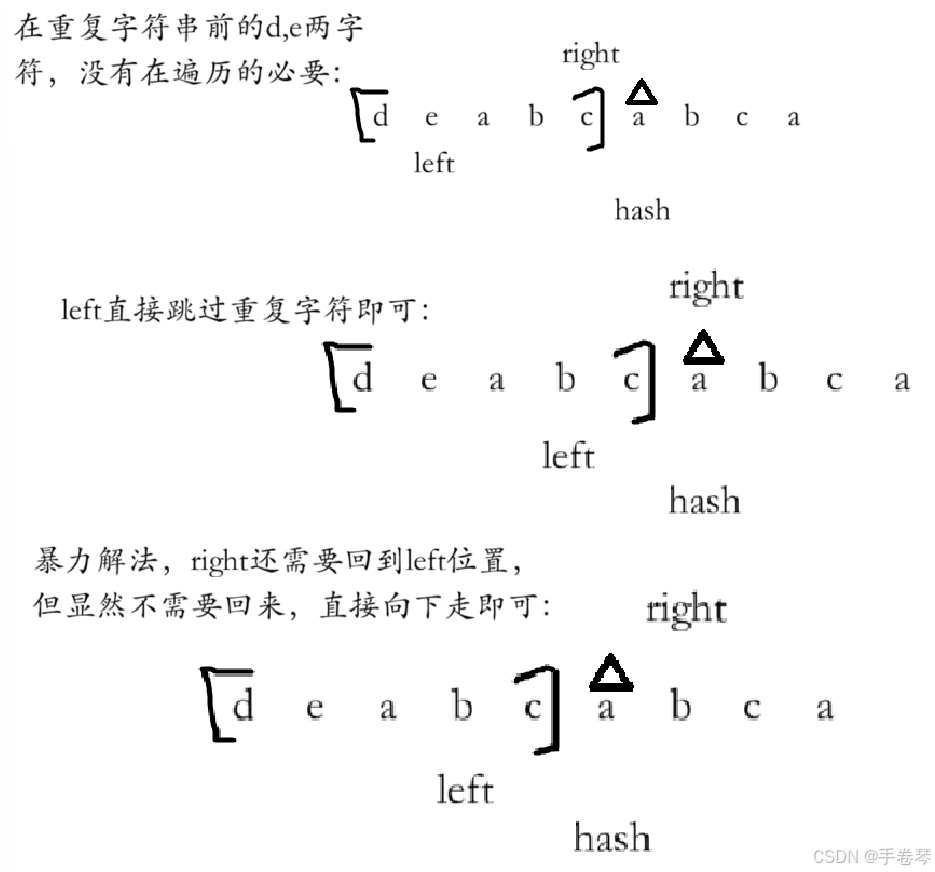
本题做法
1.left = 0, right = 0
2,进窗口 -> 让字符进入哈希表
3.判断 -> 窗口内出现重复字符 -> 出窗口 -> 判断,直至没有重复字符
出窗口(根据题决定顺序)-> 从哈希表中删除该字符
4.更新结果
代码
class Solution
{
public:
int lengthOfLongestSubstring(string s)
{
int hash[128] = { 0 }; // 利用数组模拟哈希表
int left = 0, right = 0, n = s.size();
int ret = 0;
while(right < n)
{
hash[s[right]]++; // 进窗口,字符没有出现过为0,出现一次为1
while(hash[s[right]] > 1) // 判断
{
hash[s[left++]]--; // 出窗口
}
ret = max(ret, right - left + 1); // 更新结果
right++; //下一个字符进入
}
return ret;
}
};3.最大连续1的个数 III
https://leetcode.cn/problems/max-consecutive-ones-iii/description/

算法原理
找出数组中一段连续且最长的子数组,0的个数不超过k个
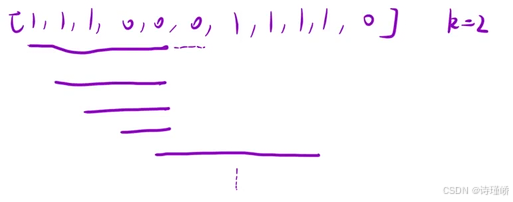
解法一:暴力枚举+zero计数器
class Solution {
public:
int longestOnes(vector<int>& nums, int k)
{
int n = nums.size();
int maxlen = 0;
for(int i = 0; i < n; i++)
{
int zero = 0;
for(int j = i; j < n; j++)
{
if(nums[j] == 0) zero++;
if(zero > k) break;
maxlen = max(maxlen, j - i + 1);
}
}
return maxlen;
}
};解法二:滑动窗口
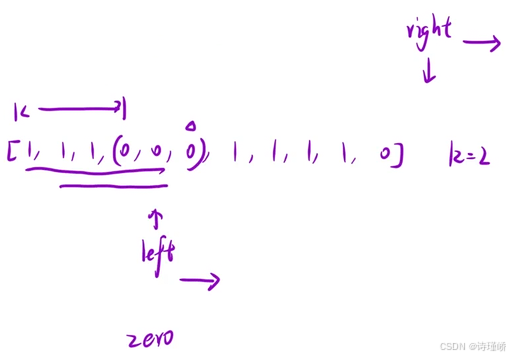
class Solution {
public:
int longestOnes(vector<int>& nums, int k)
{
int n = nums.size();
int maxlen = 0;
for(int left = 0, right = 0, zero = 0; right < n; right++)
{
if(nums[right] == 0) zero++;
while(zero > k)
if(nums[left++] == 0) zero--;
maxlen = max(maxlen, right - left + 1);
}
return maxlen;
}
};本章完。