目录
[只出现一次的数字 II](#只出现一次的数字 II)
常见位运算总结:
1.基础位运算
- &(按位与):有 0 就是 0。
- |(按位或):有 1 就是 1。
- ^(按位异或):相同为 0,相异为 1。(无进位相加)
2.给一个数 n,确定它的二进制表示中的第 x 位是 0 还是 1。(x 从 0 开始计数)
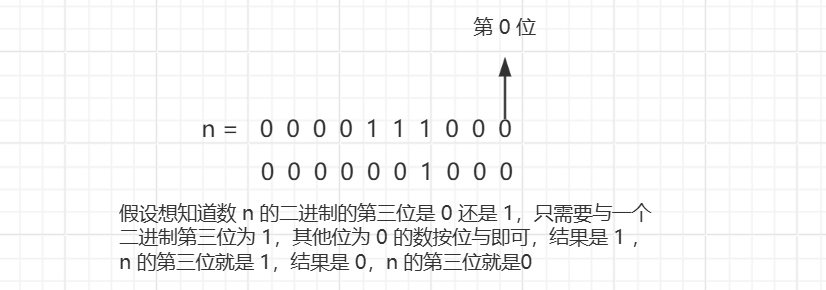
如上图所示方法,有两种方式:
- 第一种是将 1 左移 x 位,然后和 n 按位与。
- 第二种是将 n 右移 x 位,然后和 1 按位与。(通常使用第二种方式)
3.将一个数 n 的二进制表示的第 x 位修改成 1。(x 从 0 开始计数)
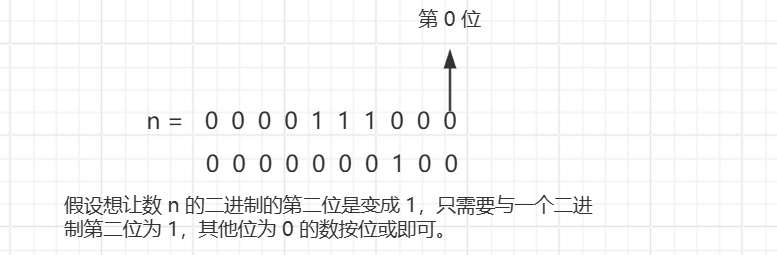
与 n 按位或的这个数字只需要将 1 左移 x 位即可得到。( 即 n = n | (1 << x ) )
4.将一个数 n 的二进制表示的第 x 位修改成 0。(x 从 0 开始计数)
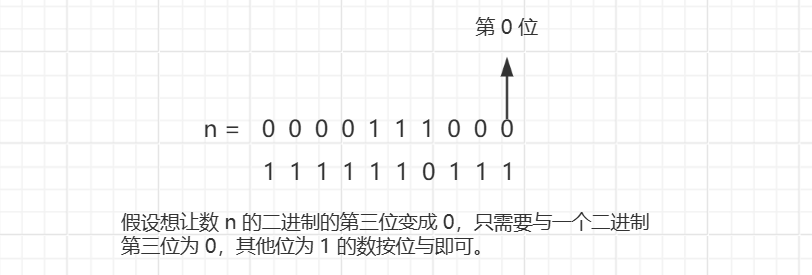
与 n 按位与的这个数字只需要将 1 左移 x 位然后按位取反即可得到。即 n = n & ( ~( 1 << x ) )
5.提取一个数(n)二进制表示中最右侧的 1。
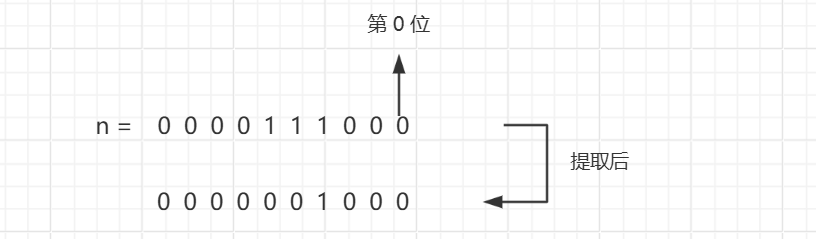
要达到上面效果,只需要 n & -n。因为 -n 的补码是 n 补码取反之后再加 1,效果就是将 n 的二进制表示中最右侧的 1 的左边的区域全都变成相反。如图所示:
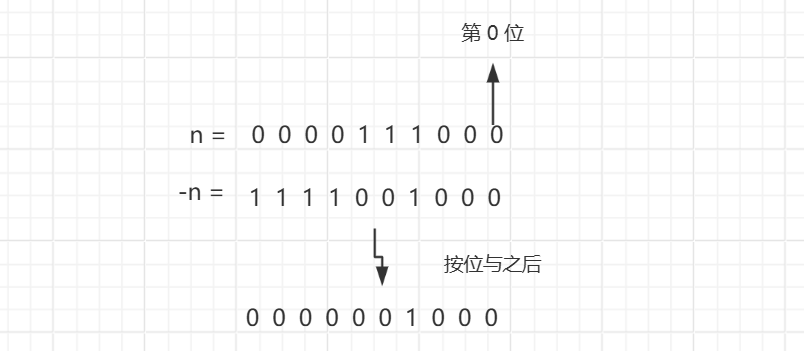
6.干掉一个数(n)二进制表示中最右侧的 1。
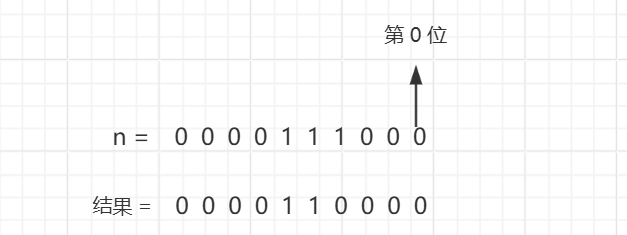
要达到上面效果,只需要 n & ( n - 1 ),n - 1 的作用是将最右侧的 1 右边的区域(包含这个 1)全部变成相反。如图所示:

7.位运算的优先级。
- 位运算中没必要去记优先级,太麻烦了,根据自己需要的计算顺序,能加括号就加括号即可。
8.异或(^)运算的运算律。
- a ^ 0 = a
- a ^ a = 0
- a ^ b ^ c = a ^ ( b ^ c )
判定字符是否唯一

**思路:**这道题可以使用一些容器进行字符和该字符出现次数的映射,就可以解决问题(哈希表,数组都可以),但是如果不想使用额外的数据结构,可以使用位图,一个 int 类型的数据有 32 个bit位,该题字符串中只有小写字母(26)个,一个 int 类型的变量充当位图就够用了。每个字符映射一个 bit 位,遍历字符串,当前字符对应 bit 位是 0,说明之前没出现过,将其置 1,如果是 1,说明前面出现过,返回 false。
**优化点:**鸽巢原理(抽屉原理)。因为小写字母只有 26 个,如果字符串长度超过 26,一定有重复字符。
代码:
cpp
class Solution {
public:
bool isUnique(string astr) {
if(astr.size() > 26)
return false;
int bitMap = 0;
for(auto ch : astr){
int i = ch - 'a';
if((bitMap >> i) & 1 == 1)
return false;
bitMap |= (1 << i);
}
return true;
}
};丢失的数字

思路:三种方法(这里使用第三种来解决)。
- 1.哈希表映射
- 2.前缀和
- 3.按位异或
**按位异或:**将数组中的元素与 0 到 n 这 n + 1 个数进行按位异或,因为相同数字按位异或后结果为 0,任何数和 0 异或都等于这个数本身,所以按位异或后的数就是丢失的那个数字
代码:
cpp
class Solution {
public:
int missingNumber(vector<int>& nums) {
int ret = 0;
for(auto num : nums)
ret ^= num;
for(int i = 0; i <= nums.size(); i++)
ret ^= i;
return ret;
}
};两整数之和
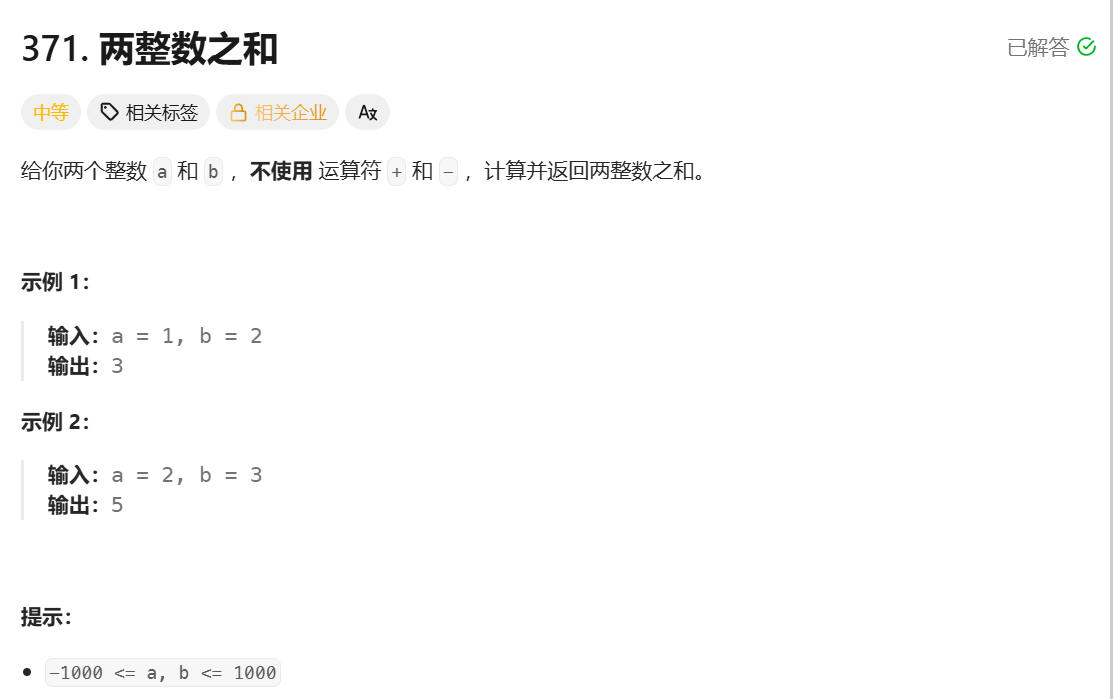
**思路:**先将两数按位异或,得到的是他们的二进制位无进位相加的结果,然后再将两个数按位与,得到需要进位的数,将这个进位的数左移一位,得到进位,不断循环这个过程,直到进位为 0,此时异或的出来的那个数就是结果。具体如图:

代码:
cpp
class Solution {
public:
int getSum(int a, int b) {
while(b != 0){
int x = a ^ b;
int carry = (a & b) << 1;
a = x;
b = carry;
}
return a;
}
};只出现一次的数字 II

**思路:**因为数组中有一个数出现一次,其他数都出现三次,所以数组中所有数同一个比特位相加有四种情况,如图:
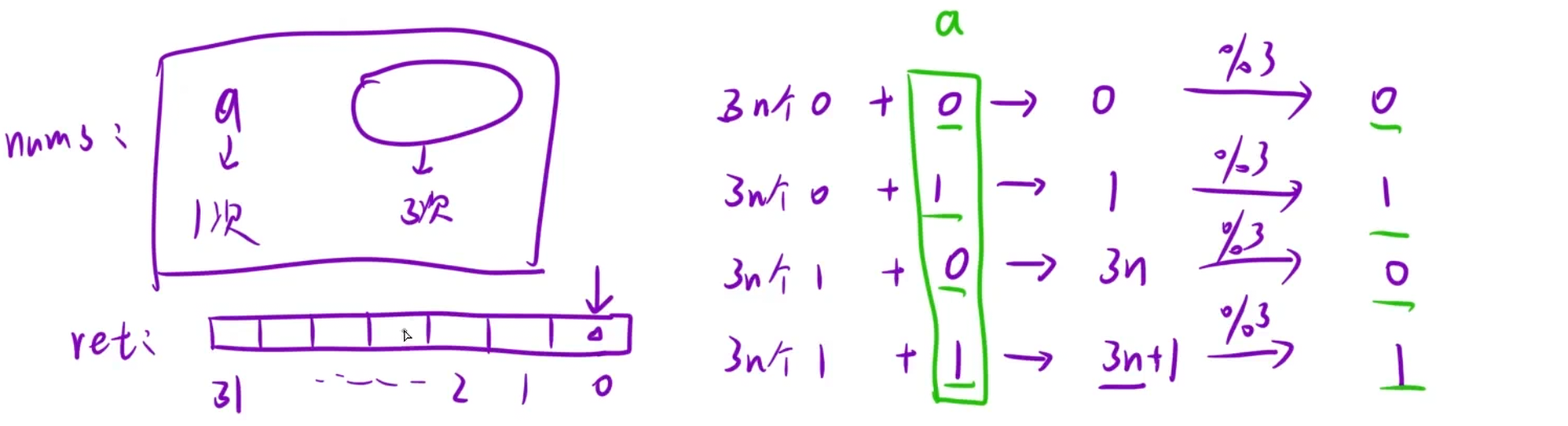
所以判断出现一次的那个数的某一个比特位是 0 还是 1,只需要把数组中所有元素的这个比特位的值相加,然后取模 3,如果是 0,出现一次的那个数的这个比特位就是 0,如果是1,出现一次的那个数的这个比特位就是1,通过这种方式,把 32 个比特位的值都算出来即可。
代码:
cpp
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ret = 0;
for(int i = 0; i < 32; i++){
int sum = 0;
for(int num : nums){
if(((num >> i) & 1) == 1){
sum++;
}
}
sum %= 3;
if(sum == 1){
ret |= 1 << i;
}
}
return ret;
}
};消失的两个数字
思路:
-
- 将数组中所有的数异或在一起,然后再和 1~N 异或在一起,这样数组中的数因为异或了两次,都等于 0,最终异或的结果其实就是消失的那两个数异或在一起了(假设将这个数存在变量 tmp 中,消失的数一个是 a,一个是 b)。
- 2.找到 tmp 中比特位为 1 的那一位二进制位,因为 tmp 是 a,b 异或的结果,所以说明 a,b 两个数中有一个数这个二进制位是 0,有一个数这个二进制位是 1(假设是第 x 位为 1)。
- 3.根据 x 位的不同,将数据划分为两部分,第 x 位是 0 的异或在一起,第 x 位是 1 的异或在一起,这样就把两个丢失的数都找到了。
代码:
cpp
class Solution {
public:
vector<int> missingTwo(vector<int>& nums) {
int tmp = 0;
for(auto num : nums)
tmp ^= num;
for(int i = 1; i <= nums.size() + 2; i++)
tmp ^= i;
int diff = 0;
for(int i = 0; i < 32; i++){
if(((tmp >> i) & 1) == 1){
diff = i;
break;
}
}
int a = 0;
int b = 0;
for(auto num : nums){
if(((num >> diff) & 1) == 1){
b ^= num;
}
else{
a ^= num;
}
}
for(int i = 1; i <= nums.size() + 2; i++){
if(((i >> diff) & 1) == 1){
b ^= i;
}
else{
a ^= i;
}
}
return {a, b};
}
};