复数
复数的几种表示方法如下
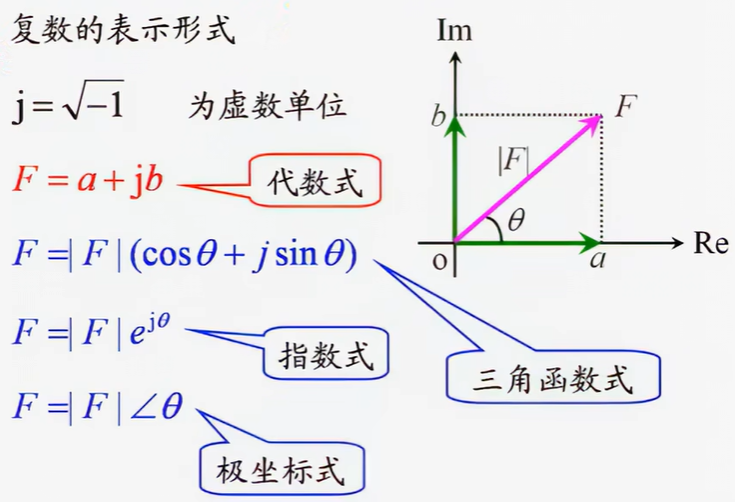
其中,Re是代表实轴,Im代表虚轴
Re又称为起始轴,从它开始旋转角度θ\thetaθ(称为辐角),逆时针为正,顺时针为负
由第二和第三个式子可以引出欧拉公式,如下
欧拉公式:ejθ=cosθ+jsinθcosθ=ejθ+e−jθ2sinθ=ejθ−e−jθ2j \begin{align} 欧拉公式: & e^{j\theta}=\cos \theta+j\sin \theta \\ & \cos \theta=\frac{e^{j\theta}+e^{-j\theta}}{2} \\ & \sin \theta=\frac{e^{j\theta}-e^{-j\theta}}{2j} \end{align} 欧拉公式:ejθ=cosθ+jsinθcosθ=2ejθ+e−jθsinθ=2jejθ−e−jθ

复数乘除运算

向量法
正弦稳态
对于由RLC构成的一般电路,求解电路响应时都能列成微分方程求解,而一阶,二阶微分方程的特解都是和等号右端的函数形式一致的(非齐次微分方程求解的规律)。由之前对一,二阶电路的分析可知,等号右端就是电路的激励,所以如果激励换成正弦信号时,其对应的特解也一定是同频率的正弦量,但幅值和初相可能不一样。这一结论具有普遍意义,即
正弦稳态 :线性非时变电路在正弦电源激励下,各支路电压、电流的特解都是与激励同频率 的正弦量,当电路中存在多个同频率的正弦激励时,结论依然成立。工程上将电路的这一特解状态称为正弦电流电路的稳定状态,简称为正弦稳态。
微分方程的特解对应的就是电路稳定时的状态,而通解对应的是非稳态时的变化规律
由此可知,对于处于正弦稳态的电路,其频率都相等,那么电路的稳态响应只与幅值和初相有关了。
引入
假设激励为us=2Uscos(ωt+ϕu)u_{s}=\sqrt{ 2 }U_{s}\cos(\omega t+\phi_{u})us=2 Uscos(ωt+ϕu)
对于RLC串联电路,将电路电流i作为响应,那么它的响应i可以设为(和激励同形式)
i=2Icos(ωt+ϕi)i=\sqrt{ 2 }I\cos(\omega t+\phi_{i})i=2 Icos(ωt+ϕi)
然后将i带入到回路的二阶微分方程就能解出特解,不过求解时就会碰到正弦函数的加减运算,而正弦函数的加减是很麻烦的(和差化积),对于二阶可以勉强求一求,但是对于复杂点电路求解会变得很复杂,有牛人为了解决这个问题提出了向量法,将正弦函数变为向量去计算,然后再将向量计算结果反过来变成正弦函数。而向量的加减乘除都很好计算,上面的问题就解决了!(牛人就是牛)
由于向量只有两个变量,所以能转化成向量计算的前提也是电路在正弦稳态
向量的加减可以用代数形式来计算,向量的乘除可以用指数形式来计算,都很方便
向量表示正弦函数
具体做法就是,构造一个复函数
f(t)=2Iej(ωt+ϕ) f(t)=\sqrt{ 2 }Ie^{j(\omega t+\phi)} f(t)=2 Iej(ωt+ϕ)
根据欧拉公式,其又可写成
f(t)=2Icos(ωt+ϕ)+j2Isin(ωt+ϕ) f(t)=\sqrt{ 2 }I\cos(\omega t+\phi)+j\sqrt{ 2 }I\sin(\omega t+\phi) f(t)=2 Icos(ωt+ϕ)+j2 Isin(ωt+ϕ)
可以看出其实部就是要求的响应i
Re[f(t)]=2Icos(ωt+ϕi)=i \mathrm{Re}[f(t)]=\sqrt{ 2 }I\cos(\omega t+\phi_{i})=i Re[f(t)]=2 Icos(ωt+ϕi)=i
这个复函数中的I,ω,ϕI,\omega,\phiI,ω,ϕ和正弦函数都是一一对应的,到这里其实就已经实现了从正弦到复函数的转换,但对于正弦稳态电路,频率都是一样的,不需要ω\omegaω这个变量,所以将f(t)f(t)f(t)进一步拆分
f(t)=2∗Iejϕ∗ejωt=I˙ejωt f(t)=\sqrt{ 2 }*\textcolor{red}{Ie^{j\phi}}*e^{j\omega t}=\dot{I}e^{j\omega t} f(t)=2 ∗Iejϕ∗ejωt=I˙ejωt
I˙=Iejϕ\dot{I}=Ie^{j\phi}I˙=Iejϕ称为复常数,这个常数包含I和ϕI和\phiI和ϕ,和正弦函数一一对应,I˙\dot{I}I˙又可以写成I˙=I∠ϕ,I\dot{I}=I∠\phi,II˙=I∠ϕ,I为正弦函数有效值。那么正弦函数和复常数就有如下对应关系
i=2Icos(ωt+ϕ)⇌ωI∠ϕ,I为有效值 i=\sqrt{ 2 }I\cos(\omega t+\phi) \underset{\omega }{\rightleftharpoons} I∠\phi,I为有效值 i=2 Icos(ωt+ϕ)ω⇌I∠ϕ,I为有效值
在从复函数变回正弦函数时要加上角频率ω\omegaω
以上对应关系并不是只对电流i生效的,每个正弦函数都有自己对应的复函数f(t)f(t)f(t)以及对应的复常数
运算
加减运算
已经实现了用向量表示正弦函数,但是正弦函数的加减能对应向量的加减吗?答案是可以的,证明
i1(t)=2I1cos(ωt+ϕ1)=Re(2I1˙ejωt)i2(t)=2I2cos(ωt+ϕ2)=Re(2I2˙ejωt)i(t)=i1(t)+i2(t)=Re(2I1˙ejωt)+Re(2I2˙ejωt)=Re(2(I1˙+I2˙)ejωt) \begin{align} & i_{1}(t)=\sqrt{ 2 }I_{1}\cos(\omega t+\phi_{1})=\mathrm{Re}(\sqrt{ 2 }\dot{I_{1}}e^{j\omega t}) \\ & i_{2}(t)=\sqrt{ 2 }I_{2}\cos(\omega t+\phi_{2})=\mathrm{Re}(\sqrt{ 2 }\dot{I_{2}}e^{j\omega t}) \\ i(t)& =i_{1}(t)+i_{2}(t) =\mathrm{Re}(\sqrt{ 2 }\dot{I_{1}}e^{j\omega t})+\mathrm{Re}(\sqrt{ 2 }\dot{I_{2}}e^{j\omega t}) \\ & =\mathrm{Re}(\sqrt{ 2 }(\dot{I_{1}}+\dot{I_{2}})e^{j\omega t}) \end{align} i(t)i1(t)=2 I1cos(ωt+ϕ1)=Re(2 I1˙ejωt)i2(t)=2 I2cos(ωt+ϕ2)=Re(2 I2˙ejωt)=i1(t)+i2(t)=Re(2 I1˙ejωt)+Re(2 I2˙ejωt)=Re(2 (I1˙+I2˙)ejωt)
看到同频率正弦函数的加减就是对应向量的加减 ,将向量结算结果再转化成正弦函数形式就完成了计算。
积分微分
同理,微分和积分有如下关系

最后jωI˙j\omega \dot{I}jωI˙化简时,将jωj\omegajω看成一个向量,它是一个旋转因子,j旋转π2\frac{\pi}{2}2π。它和向量I˙\dot{I}I˙相乘,得到上图结果。同理-j旋转为−π2-\frac{\pi}{2}−2π
notes
- 构造的这个函数很关键,牛人就是牛人,能想到这个函数,相当于干活干的不得劲就自己造了个工具
- 用向量表示时这里用的是有效值,当然也可以用最大值,但常用有效值表示
- 可以扩展到所有频率相同的正弦函数的运算
- 用正弦函数写对应向量时,要满足下面三个条件
- 写成cos函数
- 最左侧幅值部分要为正
- ωt\omega tωt要一致
有了以上方法,再来看RLC组成的微分方程
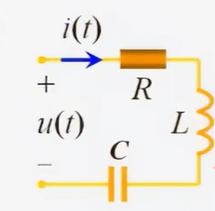
激励为u(t)u(t)u(t),响应为i(t)i(t)i(t),列出微分方程
u(t)=Ri+Ldidt+1C∫idt用向量表示U˙=RI˙+jωLI˙+I˙jωC\begin{align} & u(t) =Ri+L\frac{di}{dt}+\frac{1}{C}\int idt \\ \text{用向量表示} \\ & \dot{U}=R \dot{I}+j\omega L \dot{I}+\frac{\dot{I}}{j\omega C} \end{align} 用向量表示u(t)=Ri+Ldtdi+C1∫idtU˙=RI˙+jωLI˙+jωCI˙
直接变成向量的求和了,变得非常简单。(妙啊)
电路定律的向量形式
当激励源是正弦函数时
电阻R的VCR :U˙=RI˙\dot{U}=R\dot{I}U˙=RI˙
有效值:U=RIU=RIU=RI
相位:ϕu=ϕi\phi_{u}=\phi_{i}ϕu=ϕi电压电流同向
功率:频率为2ω2\omega2ω,整个周期内一直耗能
电感 :UL˙=jωLI˙=jXLI˙,XL=ωL是感抗\dot{U_{L}}=j\omega L\dot{I}=jX_{L}\dot{I},X_{L}=\omega L是感抗UL˙=jωLI˙=jXLI˙,XL=ωL是感抗
有效值:U=ωLIU=\omega LIU=ωLI
相位:ϕu=ϕi+90°\phi_{u}=\phi_{i}+90°ϕu=ϕi+90°,电感电压超前电流90°相位
功率:频率为2ω2\omega2ω,一个周期内正半周和负半轴抵消,表明电感只储能,不耗能
电容 :U˙C=1jωCI˙=jXCI˙,XC=−1ωC是容抗\dot{U}{C}=\frac{1}{j\omega C}\dot{I}=jX{C}\dot{I}, X_{C}=-\frac{1}{\omega C}是容抗U˙C=jωC1I˙=jXCI˙,XC=−ωC1是容抗
有效值:U=1ωCIU=\frac{1}{\omega C}IU=ωC1I
相位:ϕi=ϕu+90°\phi_{i}=\phi_{u}+90°ϕi=ϕu+90°,电容电流超前电压90°相位
功率:频率为2ω2\omega2ω,一个周期内正半周和负半轴抵消,表明电容只储能,不耗能
基尔霍夫定律的向量形式
基尔霍夫定律(KCL,KVL)在向量形式中也成立,即
∑(I1˙+I2˙+⋯+In˙)=0∑(U1˙+U2˙+⋯+Un˙)=0\begin{align} & \sum(\dot{I_{1}}+\dot{I_{2}}+\dots+\dot{I_{n}})=0\\ & \sum(\dot{U_{1}}+\dot{U_{2}}+\dots+\dot{U_{n}})=0 \end{align} ∑(I1˙+I2˙+⋯+In˙)=0∑(U1˙+U2˙+⋯+Un˙)=0
前提是要满足能用向量法表示,也即处于正弦稳态
例1 :如图

i(t)i(t)i(t)写成向量形式:I˙=5∠15°\dot{I}=5∠15°I˙=5∠15°,则
U˙S=U˙R+U˙C=I˙(R+jXC)=5∠15°(5−j1106∗0.2∗10−6)=5∠15°(5−5j)将5−5j写成极坐标形式=5∠15°∗52∠−45°=252∠−30°V再写回正弦函数形式uS=50cos(106t−30°)\begin{align} \dot{U}{S} & =\dot{U}{R}+\dot{U}{C} \\ & =\dot{I}(R+jX{C}) \\ & =5∠15°\left( 5-j\frac{1}{10^{6}*0.2*10^{-6}} \right) \\ & =5∠15°\left( 5-5j\right) \\ 将5-5j写成极坐标形式\\ & =5∠15°*5\sqrt{ 2 }∠-45° \\ & =25\sqrt{ 2 }∠-30°V \\ \\ 再写回正弦函数形式 \\ & u_{S}=50\cos(10^6t-30°) \end{align} U˙S将5−5j写成极坐标形式再写回正弦函数形式=U˙R+U˙C=I˙(R+jXC)=5∠15°(5−j106∗0.2∗10−61)=5∠15°(5−5j)=5∠15°∗52 ∠−45°=252 ∠−30°VuS=50cos(106t−30°)note
- 用到向量的乘法,也即复数的乘法,所以化成极坐标形式
- uSu_{S}uS并不是简单的阻抗和容抗相加和电流的乘积,这里是有向量的,有方向存在
例2 :如图
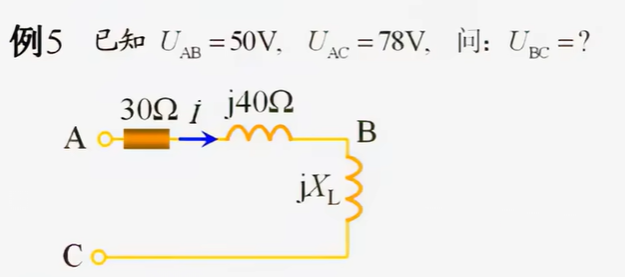
首先,不能直接得出BC的电压就是28V,因为给出的AB以及AC的电压是电压的有效值,并不是电路的稳态值,如果电路处于稳态BC电压就是0V了,还求啥。列出对应向量图
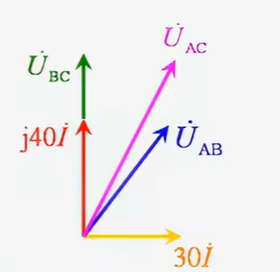
求解如下,设I˙=I∠θ\dot{I}=I∠\thetaI˙=I∠θ
U˙AB=30I∠θ+j40I∠θ=(30I+40Ij)∠θ∣U˙AB∣=∣30I+40Ij∣=(30I)2+(40I)2=50V得到,I=1AU˙AC=(30+j(40+XL))∠θ∣U˙AC∣=(30)2+(40+XL)2=78 ⟹ XL=32Ω ⟹ UAB=IXL=32V\begin{align} \dot{U}{AB} & =30I\angle \theta+j 40I\angle \theta=(30I+40Ij)\angle\theta \\ |\dot{U}{AB}| & =|30I+40Ij|=\sqrt{ (30I)^2+(40I)^2 }=50V \\ 得到,I & =1A \\ \dot{U}{AC} & =(30+j(40+X{L}))\angle \theta \\ |\dot{U}{AC}| & =\sqrt{ (30)^2+(40+X{L})^2 }=78 \\ \implies & X_{L}=32Ω \\ \implies & U_{AB}=IX_{L}=32V \end{align}U˙AB∣U˙AB∣得到,IU˙AC∣U˙AC∣⟹⟹=30I∠θ+j40I∠θ=(30I+40Ij)∠θ=∣30I+40Ij∣=(30I)2+(40I)2 =50V=1A=(30+j(40+XL))∠θ=(30)2+(40+XL)2 =78XL=32ΩUAB=IXL=32V