从,
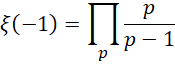
右侧表达的是顶层的单位1和底层的周期(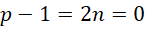 )之间的关系,以及哥德巴赫猜想,
)之间的关系,以及哥德巴赫猜想,
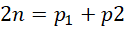
可以意识到,
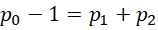
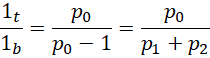
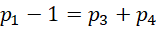
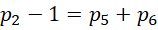
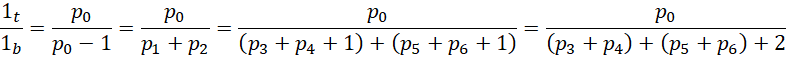
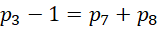
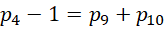
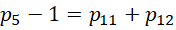
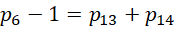
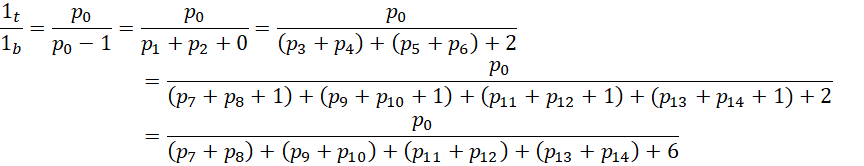
这个比例中,分子总是1项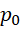 ,分母则从最开始的1项,变成2项,变成4项,变成8项,也就是说,分母的项数符合,
,分母则从最开始的1项,变成2项,变成4项,变成8项,也就是说,分母的项数符合,
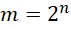
项后面的常数,从-1,到0,到2,到6,符合首项是增量,
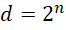
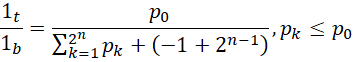
其中,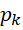 并不保证是小于
并不保证是小于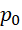 的所有质数,可能一部分就够了,可能还有重复。
的所有质数,可能一部分就够了,可能还有重复。
所以直接认为,
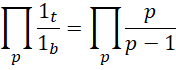
是没有道理的,方程左右两边可能具有随着质数增加而变化的比例关系。也就是说,
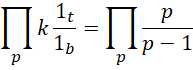
这里的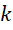 是本来就存在的。但是它的存在也提示我们,可以人为的改动它,比如找到下一个质数,并将其乘入质数全乘积,这个数值就可能会改变。
是本来就存在的。但是它的存在也提示我们,可以人为的改动它,比如找到下一个质数,并将其乘入质数全乘积,这个数值就可能会改变。
我们知道,在常规前提下,角度的单周期最大值就是顶层和底层之间单位的比率,这个比率就是圆周率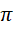 ,
,
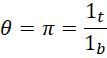
在有限的上下层之间,这个比率的精度也是有限的。现在,我们可以通过对系统增加新的质数,来扩展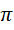 的精度,或者说增加它的数值(精度提高就要增加更多位数,相当于原来小数位上的零变成了非0,数值整体就增大了),此时假定
的精度,或者说增加它的数值(精度提高就要增加更多位数,相当于原来小数位上的零变成了非0,数值整体就增大了),此时假定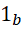 不变,
不变,
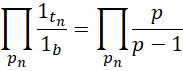
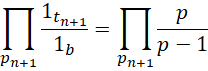
假定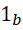 不变,
不变,
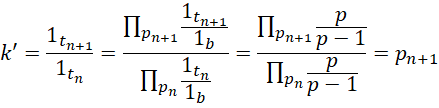
所以增加圆周率的精度,核心就在于寻找到下一个质数。而这就增加了周期的深度,或者说多分复数的位数,而这又叫做增加了新的维数。这就是发现并应用新的质数和维数提升之间的关系。随着过程的继续,显然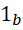 也会随之变化,最终重新回到稳定的状态,也就是k回归到原来的数值,
也会随之变化,最终重新回到稳定的状态,也就是k回归到原来的数值,
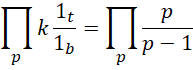
所以说出现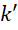 并不是常见的现象。但由于诸多质数的存在,出现新的,
并不是常见的现象。但由于诸多质数的存在,出现新的,
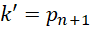
也是一定会发生的事情,只是不知道在什么时候,如何发生。
但能猜到的是,现有的质数越多发生得越快越早。
所以这种周期扩展的速率,也是呈指数增长的。
回到,
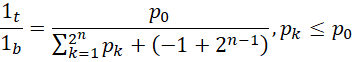
如果认为,
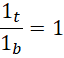
那么,
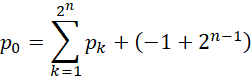
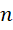 从1开始,导致质数减去1作为的周期表现为两个质数的和。从对哥德巴赫猜想的分析中我们可以认识到,这两个质数作为单位,也就是构成的倒数之和在另外两个整数的配合之下,又可以构成各种偶数周期。这就使得质数
从1开始,导致质数减去1作为的周期表现为两个质数的和。从对哥德巴赫猜想的分析中我们可以认识到,这两个质数作为单位,也就是构成的倒数之和在另外两个整数的配合之下,又可以构成各种偶数周期。这就使得质数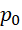 通过分裂为多个质数对,而对应出不同类型的周期构造模式。再在这些模式中使用两个整数即可创造这些模式的不同实例。在这些模式的特定实例中,单位再次作为更低层次的顶层,进而可以创造更低层次的周期类型族。这个过程上不封顶,下不见底,原则上可以构造可能想到的一切周期和周期组合。
通过分裂为多个质数对,而对应出不同类型的周期构造模式。再在这些模式中使用两个整数即可创造这些模式的不同实例。在这些模式的特定实例中,单位再次作为更低层次的顶层,进而可以创造更低层次的周期类型族。这个过程上不封顶,下不见底,原则上可以构造可能想到的一切周期和周期组合。