回到问题本身,计算具体的数值,比如要求 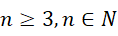 ,假定
,假定
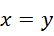
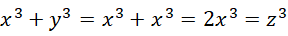
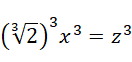
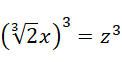
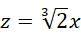
系数是 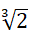 ,显然
,显然 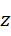 和
和 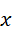 不同为整数。再扩展一些,假定,
不同为整数。再扩展一些,假定,
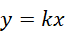
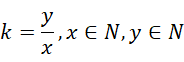
则 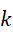 为有理数(可比数),
为有理数(可比数),
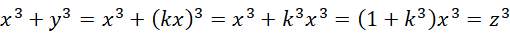
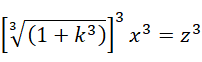
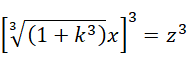
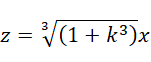
如果 z 和 x 以及 y 一样都是整数,那么,
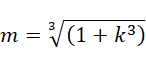
必须为有理数。也就是说,
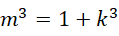
之中, 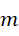 和
和 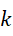 都是有理数,也就是都是两个整数的比值。再扩展一下,
都是有理数,也就是都是两个整数的比值。再扩展一下,
对于 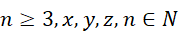 ,方程,
,方程,
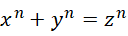
成立,则必须有,
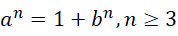
其中的 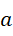 和
和 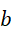 都是有理数。都可以写成两个整数之比的形式,
都是有理数。都可以写成两个整数之比的形式,
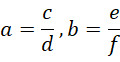
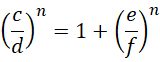
如果此时 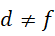 ,那么方程就变成了
,那么方程就变成了 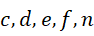 五个整数之间的关系。这不是解方程,而是使得方程变得更为复杂,所以无论如何必须要求
五个整数之间的关系。这不是解方程,而是使得方程变得更为复杂,所以无论如何必须要求
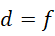
才能使得关于 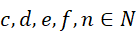 的方程化简为
的方程化简为 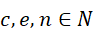 ,也就是三个未知整数的方程。但
,也就是三个未知整数的方程。但 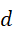 和
和 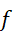 的相等是没法要求的,可是我们可以要求两个有理数,使得它们变成通分的形式,
的相等是没法要求的,可是我们可以要求两个有理数,使得它们变成通分的形式,
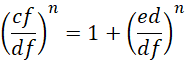
我们此时把 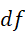 当成一个单位即可,
当成一个单位即可,
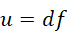
这样就得到关于 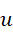 的方程,
的方程,
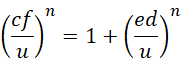
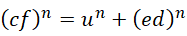
看似回到原来的方程,而且未知数多了一个,但是这里出现了新的条件:若要原方程有解,则需要其中至少两个未知数为合数,
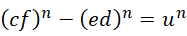
且在两个数为合数的前提下写成减法形式。由此引入虚数单位,
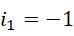
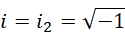
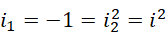
得到,
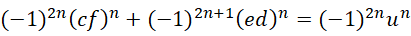
以及,
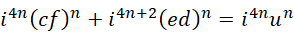
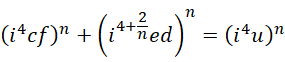
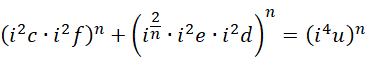
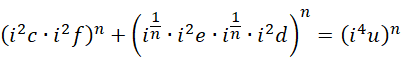
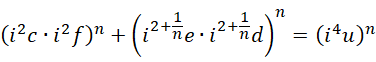
如果,
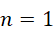
可以得到,
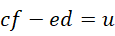
左边的整数任取,右边的整数随之变动即可,五个整数都可以获得。如果,
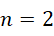
代入方程,
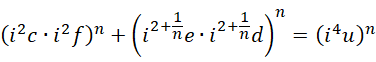
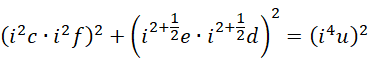
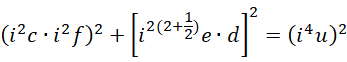
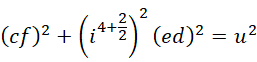
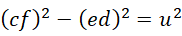
这可以退回到,
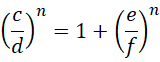
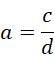
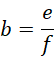
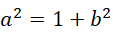
也就是,
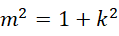
最后退回到,
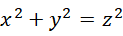
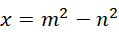
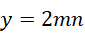
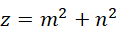
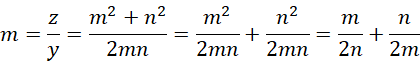
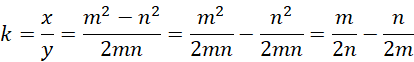
可见 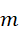 和
和 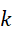 都是有理数。继续,如果,
都是有理数。继续,如果,
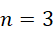
代入方程,
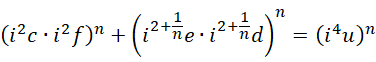
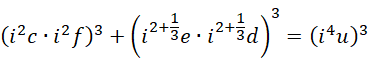
对比,
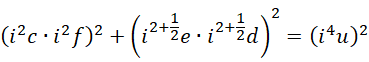
差别在于,
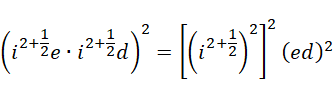
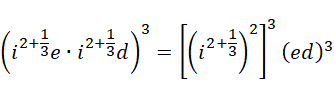
也就是说,对于虚数单位的幂次,虽然二次幂之后再三次幂和三次幂之后再二次幂的结果是相同的,但是二次幂对应于 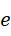 和
和 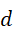 两个整数的各自分配,但三次幂分配给两个整数,无法均分,对于高次的情况,
两个整数的各自分配,但三次幂分配给两个整数,无法均分,对于高次的情况,
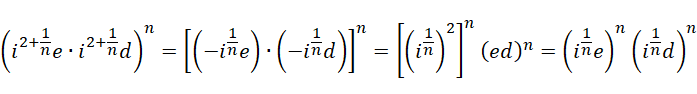
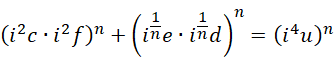
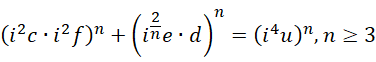
中间项关于虚数单位的系数, 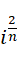 在
在 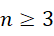 的时候不是虚数单位的整数次幂(幂次小于1),而且它也无法平均分配为各项(比如
的时候不是虚数单位的整数次幂(幂次小于1),而且它也无法平均分配为各项(比如 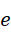 和
和 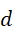 )的系数,比如,
)的系数,比如,
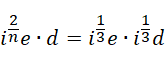
就算作为 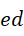 整体的系数,也不是虚数单位的整数幂次,
整体的系数,也不是虚数单位的整数幂次,
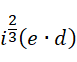
这种形式会导致至少一项的系数分配到的虚数单位的幂次非整数,而是某种 0 到 1 之间的残留余量,而且这个幂次是负的。假定分配方式为,
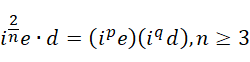
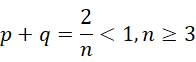
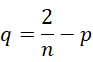
两者相比判断结果的符号,
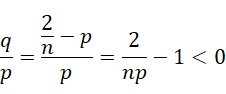
也就是说, 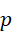 和
和 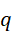 异号,假定选择
异号,假定选择 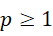 为整数,则
为整数,则 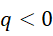
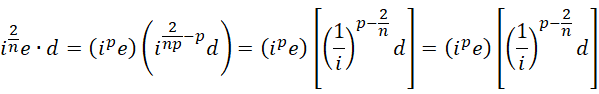
也就是说,关于 d 的虚数单位(作为系数),
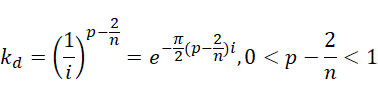
比如 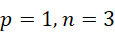 ,得到的是,
,得到的是,
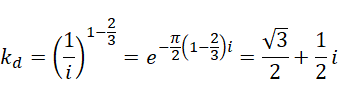
显然这是一个复数。但如果发生的是,
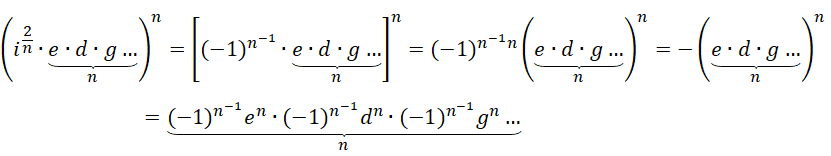
虚数单位的幂次就可以完全分配, 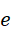 和
和 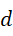 等数值的系数就都可以是整数,结果就有整数解。所以,
等数值的系数就都可以是整数,结果就有整数解。所以,
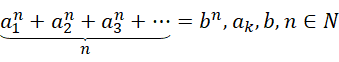
总是成立的。
为什么一个方程在整数前提下或者有理数以至于实数前提下无解,一旦引入复数,就几乎都有解?(当然有些方程无论引入什么数都无解,比如 0=1 )
那是因为,根据虚数单位的定义,
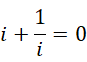
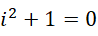
这里的 0 作为周期,总是可以加入到方程里面,而 0 可以指定任何数值作为周期,那么虚数单位就可以由此从一个数值滑动到一个更大的或者更小的数值,比如,可以通过这种方式,
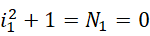
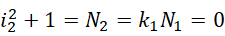
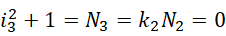
实现虚数单位的数值的滑动,
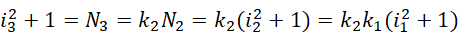
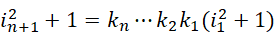
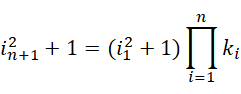
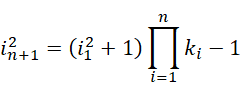
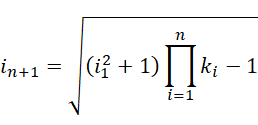
有了这种滑动能力,几乎任何方程都可以通过有限或者无限次的滑动,使得两边趋向同一个值,也就是使得方程成立。
还有其它方法,比如,把 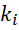 放在幂次上,
放在幂次上,
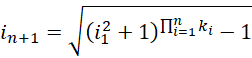
甚至放在指数塔上,
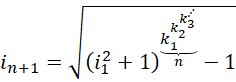
这些做法实际上就是任意个 0 的相加等于 0 , 0 的任意次等于 0,0 的任意高次指数塔等于 0 的应用。