GRPO 算法演进——奖励设计篇

文章目录

一、引言
二、奖励设计篇
- [2.1 S-GRPO](#2.1 S-GRPO)
- [2.2 SEED-GRPO](#2.2 SEED-GRPO)
- [2.3 GRPO-λ 1 ^1 1](#2.3 GRPO-λ 1 ^1 1)
- [2.4 EDGE-GRPO](#2.4 EDGE-GRPO)
- [2.5 CAPO](#2.5 CAPO)
- [2.6 COPO](#2.6 COPO)
- [2.7 GTPO 2 ^2 2](#2.7 GTPO 2 ^2 2)
- [2.8 MAPO](#2.8 MAPO)
- [2.9 NGRPO](#2.9 NGRPO)
- [2.10 GRPO-λ 2 ^2 2](#2.10 GRPO-λ 2 ^2 2)
- [2.11 λ-GRPO](#2.11 λ-GRPO)
- [2.12 FAPO](#2.12 FAPO)
- [2.13 SAPO](#2.13 SAPO)
三、相关文章

一、引言

Group Relative Policy Optimization（GRPO）凭借其无需价值网络、组内相对估计的优势，成为大语言模型强化学习的主流范式。然而，随着研究的深入，GRPO 在奖励稀疏性、样本效率、探索-利用平衡等方面的问题逐渐显现。

研究者们从奖励设计 这一核心维度出发，提出了一系列创新性改进方案。从 S-GRPO 的序列化早退奖励到 SEED-GRPO 的语义熵感知调节，从 EDGE-GRPO 的熵驱动优势修正到 CAPO 的细粒度过程奖励，再到 FAPO 的缺陷感知阶段转换------这些工作共同勾勒出 GRPO 奖励策略的大致演进图景：从二元结果奖励到多维度过程奖励，从静态固定奖励到动态自适应奖励，从粗粒度组级奖励到细粒度 token 级奖励。

本文系统梳理 13 项代表性工作（S-GRPO, SEED-GRPO, GRPO-λ 1 ^1 1, EDGE-GRPO, CAPO, COPO, GTPO 2 ^2 2, MAPO, NGRPO, GRPO-λ 2 ^2 2, λ-GRPO, FAPO, SAPO），深入剖析其设计思想与数学机制。

算法名称	发布时间	算法完整名称	论文链接
S-GRPO	2025.05	Serial-Group Decaying-Reward Policy Optimization	https://arxiv.org/abs/2505.07686
SEED-GRPO	2025.05	Semantic Entropy EnhanceD Group Relative Policy Optimization	https://arxiv.org/abs/2505.12346
GRPO-λ 1 ^1 1	2025.05	Group Relative Policy Optimization with dynamic λ-threshold switching	https://arxiv.org/abs/2505.18086
EDGE-GRPO	2025.07	Entropy-Driven Group Relative Policy Optimization with Guided Error Correction	https://arxiv.org/abs/2507.21848
CAPO	2025.08	Credit Assignment Policy Optimization	https://arxiv.org/abs/2508.02298
COPO	2025.08	Consistency-Aware Policy Optimization	https://arxiv.org/abs/2508.04138
GTPO 2 ^2 2	2025.08	Group Token Policy Optimization	https://arxiv.org/abs/2508.04349
MAPO	2025.09	Mixed Advantage Policy Optimization	https://arxiv.org/abs/2509.18849
NGRPO	2025.09	Negative-enhanced Group Relative Policy Optimization	https://arxiv.org/abs/2509.18851
GRPO-λ 2 ^2 2	2025.10	Group Relative Policy Optimization with λ-return eligibility traces	https://arxiv.org/abs/2510.00194
λ-GRPO	2025.10	Unified Group Relative Policy Optimization with learnable λ	https://arxiv.org/abs/2510.06870
FAPO	2025.10	Flawed-Aware Policy Optimization	https://arxiv.org/abs/2510.22543
SAPO	2025.11	Soft Adaptive Policy Optimization	https://arxiv.org/abs/2511.20347

二、奖励设计篇

2.1 S-GRPO

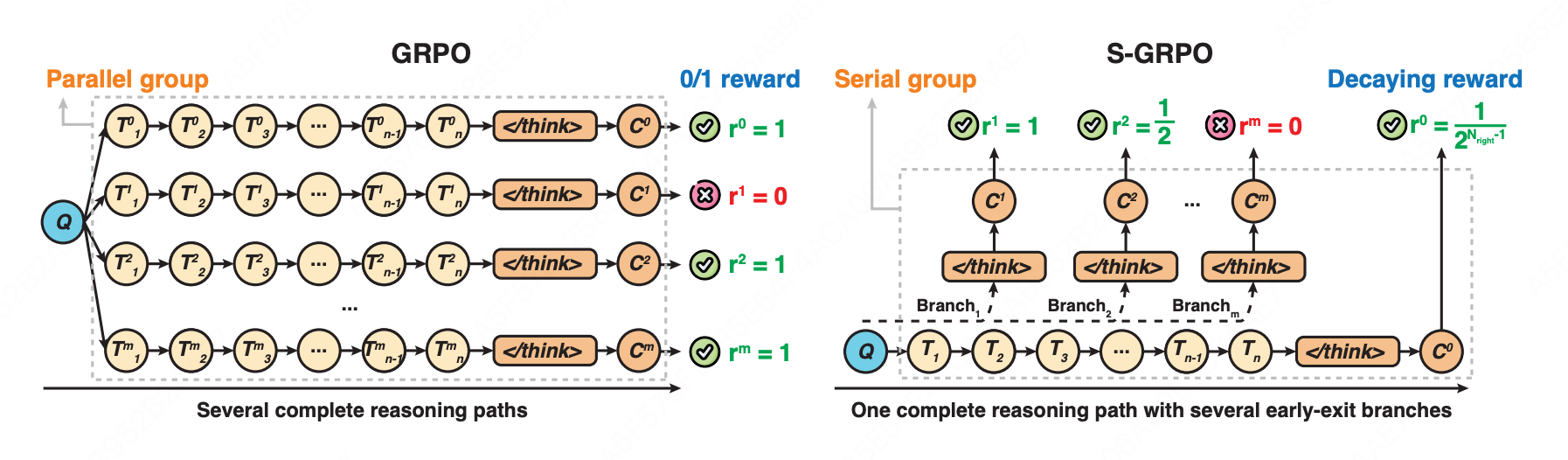
核心思想：在单条推理路径上设置多个早退检查点形成"序列组"，并对越早产生的正确答案给予指数级更高奖励，使模型学会在推理充分时及时终止思考，缩短推理长度。

序列组生成
- 阶段一：Full Thought Rollout
  - 生成完整推理路径： O 0 = { T 1 , T 2 , ... , T n , < / t h i n k > , C 0 } O^0 = \{T_1, T_2, \ldots, T_n, </think>, C_0\} O0={T1,T2,...,Tn,</think>,C0}
  - 随机选择 m m m 个截断位置 P i ∼ Uniform ( 1 , n ) P_i \sim \text{Uniform}(1,n) Pi∼Uniform(1,n)
- 阶段二：Early-exit Thought Rollout
  - 在每个截断位置 P i P_i Pi 插入提示词："Time is limited, stop thinking and start answering.\n〈/think〉\n\n"
  - 生成中间答案 C 1 , C 2 , ... , C m C_1, C_2, \ldots, C_m C1,C2,...,Cm，形成序列组 { O 1 , O 2 , ... , O m , O 0 } \{O^1, O^2, \ldots, O^m, O^0\} {O1,O2,...,Om,O0}
指数衰减奖励策略

r i = { 1 2 N right − 1 , if C i is correct 0 , if C i is incorrect r^i = \begin{cases} \frac{1}{2^{N_{\text{right}}-1}}, & \text{if } C^i \text{ is correct} \\ 0, & \text{if } C^i \text{ is incorrect} \end{cases} ri={2Nright−11,0,if Ci is correctif Ci is incorrect

其中 N right N_{\text{right}} Nright 表示当前位置为止累计的正确答案数量。越早退出且正确，奖励越高（1, 1/2, 1/4, 1/8...），错误答案一律得0。

目标函数
J S-GRPO ( θ ) = E q ∼ P ( Q ) , { o i } i = 1 G ∼ π θ old ( O ∣ q ) [ 1 G ∑ i = 1 G 1 ∣ o i ∣ ∑ t = 1 ∣ o i ∣ min ⁡ [ π θ i , t π θ old i , t A ^ i , t , clip ( π θ i , t π θ old i , t , 1 − ϵ , 1 + ϵ ) A ^ i , t ] ] \mathcal{J}{\text{S-GRPO}}(\theta) = \mathbb{E}{q \sim P(Q), \{o_i\}{i=1}^G \sim \pi{\theta_{\text{old}}}(O|q)} \left[ \frac{1}{G}\sum_{i=1}^{G} \frac{1}{|o_i|}\sum_{t=1}^{|o_i|} \min\left[\frac{\pi_\theta^{i,t}}{\pi_{\theta_{\text{old}}}^{i,t}}\hat{A}{i,t}, \text{clip}\left(\frac{\pi\theta^{i,t}}{\pi_{\theta_{\text{old}}}^{i,t}}, 1-\epsilon, 1+\epsilon\right)\hat{A}_{i,t}\right] \right] JS-GRPO(θ)=Eq∼P(Q),{oi}i=1G∼πθold(O∣q) G1i=1∑G∣oi∣1t=1∑∣oi∣min[πθoldi,tπθi,tA^i,t,clip(πθoldi,tπθi,t,1−ϵ,1+ϵ)A^i,t]

A ^ i = r i − mean ( r i ) \hat{A}_i = r_i - \text{mean}(r_i) A^i=ri−mean(ri)

2.2 SEED-GRPO

核心思想：引入"语义熵"量化模型对输入提示的不确定性，让策略更精准地匹配模型对任务难度的感知，对于模型表现出高不确定性的问题，模型更新应该更加保守。

核心流程

第一步：语义聚类

将 G G G 个采样响应 { o 1 , o 2 , ... , o G } \{o_1, o_2, \ldots, o_G\} {o1,o2,...,oG} 按语义含义分组：
- 形成 K K K 个语义簇 C = { C 1 , C 2 , ... , C K } \mathcal{C} = \{C_1, C_2, \ldots, C_K\} C={C1,C2,...,CK}
- 每个簇 C k = { o i : meaning ( o i ) = k } C_k = \{o_i : \text{meaning}(o_i) = k\} Ck={oi:meaning(oi)=k}，包含语义相同但表述可能不同的响应

第二步：计算语义熵（Semantic Entropy）

衡量模型对提示词 q q q 的不确定性：

SE ( q ) ≈ − 1 K ∑ k = 1 K log ⁡ p ( C k ∣ q ) \text{SE}(q) \approx -\frac{1}{K}\sum_{k=1}^{K}\log p(C_k \mid q) SE(q)≈−K1k=1∑Klogp(Ck∣q)

其中：

p ( C k ∣ q ) = ∑ o i ∈ C k π θ old ( o i ∣ q ) p(C_k \mid q) = \sum_{o_i \in C_k} \pi_{\theta_{\text{old}}}(o_i \mid q) p(Ck∣q)=∑oi∈Ckπθold(oi∣q) 是第 k k k 个簇的总概率质量

熵的边界：

情况	簇数量	语义熵值	含义
完全确定	K = 1 K=1 K=1（所有响应同义）	SE ( q ) = 0 \text{SE}(q) = 0 SE(q)=0	模型完全确定
极端不确定	K = G K=G K=G（每个响应都不同）	SE max ⁡ = log ⁡ G \text{SE}_{\max} = \log G SEmax=logG	模型极度不确定

第三步：不确定性感知优势调节

根据语义熵动态调整优势（advantage），实现保守更新：

A ^ i = A i ⋅ f ( α ⋅ SE ( q ) SE max ⁡ ( q ) ) \hat{A}i = A_i \cdot f\left(\alpha \cdot \frac{\text{SE}(q)}{\text{SE}{\max}(q)}\right) A^i=Ai⋅f(α⋅SEmax(q)SE(q))

其中：
- A i A_i Ai：原始优势值
- α \alpha α：敏感性超参数
- f ( ⋅ ) f(\cdot) f(⋅)：调节函数（可选线性、指数、聚焦等形式）
核心机制：
- 高熵（高不确定性）→ f ( ⋅ ) f(\cdot) f(⋅) 输出小 → 优势被压缩 → 更新更保守
- 低熵（高确定性）→ f ( ⋅ ) f(\cdot) f(⋅) 输出大 → 优势保留 → 正常更新

2.3 GRPO-λ 1 ^1 1

核心思想：通过动态调整奖励策略，平衡效率与准确率。在模型推理能力不足时，优先提升准确性，而在模型已经具备较强推理能力时，优化推理效率（应用长度惩罚奖励）。

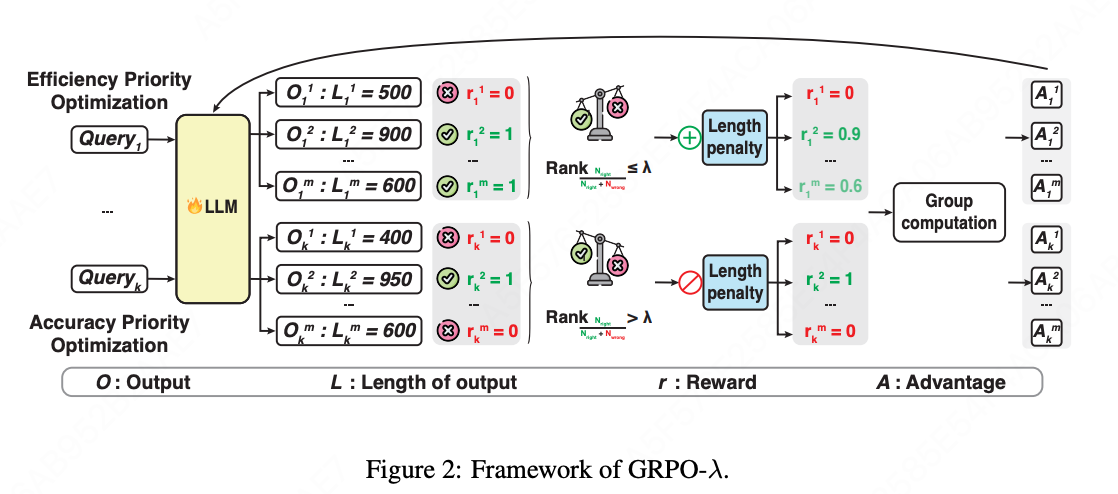
核心流程

第一步：查询采样组生成

对每个训练查询 Q k Q_k Qk，模型生成 m m m 个候选回答 { O k 1 , O k 2 , ... , O k m } \{O_k^1, O_k^2, \ldots, O_k^m\} {Ok1,Ok2,...,Okm}。每个 O k i O_k^i Oki 包含：长度 L k i L_k^i Lki 和结果奖励 r k i ∈ { 0 , 1 } r_k^i \in \{0, 1\} rki∈{0,1}
第二步：批次级 Top-λ 选择
目标：区分"已足够准确"和"仍需提升准确"的组
- 评估批次内每个查询-补全组的正确率
- 按正确率对组进行排序
- 选择 Top-λ 比例 （如前20%）→ 效率优先优化
- 剩余组 → 准确率优先优化
第三步：动态奖励策略调整

根据 Top-λ 选择结果，应用两种不同奖励策略：
- 效率优先优化（带长度惩罚）------ 针对 Top-λ 组
r k i = { 1 − α ⋅ σ ( L k i − mean ( L k ) correct std ( L k ) correct ) if O k i is correct 0 if O k i is wrong r_k^i = \begin{cases} 1 - \alpha \cdot \sigma\left(\frac{L_k^i - \text{mean}(L_k){\text{correct}}}{\text{std}(L_k){\text{correct}}}\right) & \text{if } O_k^i \text{ is correct} \\ 0 & \text{if } O_k^i \text{ is wrong} \end{cases} rki={1−α⋅σ(std(Lk)correctLki−mean(Lk)correct)0if Oki is correctif Oki is wrong
- 准确率优先优化（0/1 结果奖励）------ 针对非 Top-λ 组
r k i = { 1 if O k i is correct 0 if O k i is wrong r_k^i = \begin{cases} 1 & \text{if } O_k^i \text{ is correct} \\ 0 & \text{if } O_k^i \text{ is wrong} \end{cases} rki={10if Oki is correctif Oki is wrong

2.4 EDGE-GRPO

核心思想：通过外部引导修正错误响应（GEC）和基于策略熵精细调整优势（EDA），实现"奖励自信正确、惩罚固执错误"的自适应训练，有效缓解优势坍塌。

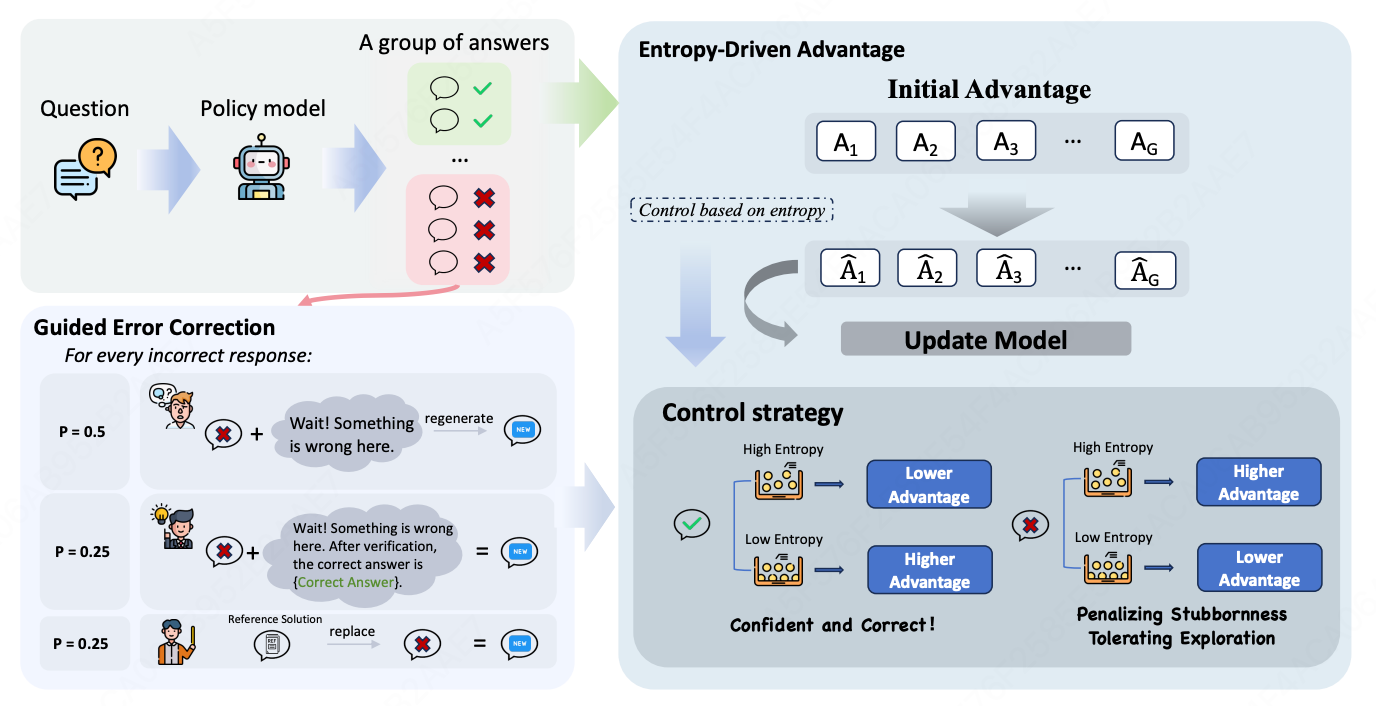
引导式错误修正（GEC）

针对错误响应，按概率执行三种操作，从根本上增强响应多样性。

操作	概率	描述
Prompt and Regenerate	P = 0.5	提供反思提示，要求模型重新生成答案
Direct Answer Injection	P = 0.25	反思提示 + 直接提供正确答案
Reference Solution Replacement	P = 0.25	完全替换为外部参考解决方案

熵驱动优势（EDA）

策略熵计算

P = − 1 T ∑ t = 1 T ∑ j = 1 V P t , j ⋅ log ⁡ P t , j P = -\frac{1}{T}\sum_{t=1}^{T}\sum_{j=1}^{V} P_{t,j} \cdot \log P_{t,j} P=−T1t=1∑Tj=1∑VPt,j⋅logPt,j

P t , j = π θ ( j ∈ V ∣ q , o < t ) = Softmax ( logits t T ) P_{t,j} = \pi_\theta(j \in V | q, o_{<t}) = \text{Softmax}\left(\frac{\text{logits}_t}{T}\right) Pt,j=πθ(j∈V∣q,o<t)=Softmax(Tlogitst)

其中 T T T 表示 response 的 tokens 的个数， V V V 表示词表大小， P t , j P_{t,j} Pt,j 表示 LLM 在第 t t t 个 token 的位置输出词 j j j 的概率。

优势计算

P ^ i = P i mean ( { P 1 , P 2 , ⋯ , P G } ) \hat{P}_i = \frac{P_i}{\text{mean}(\{P_1, P_2, \cdots, P_G\})} P^i=mean({P1,P2,⋯,PG})Pi
A ^ i = A i P ^ i \hat{A}_i = \frac{A_i}{\hat{P}_i} A^i=P^iAi
- 给正确且置信度高（低熵）的响应更高的优势，错误且置信度高的响应施加更严厉的惩罚。

2.5 CAPO

核心思想：针对 GRPO 粗粒度反馈的困境，利用现成LLM作为生成式过程奖励模型生成步骤级批判，并采用非对称的层次化奖励结构实现细粒度奖励分配。

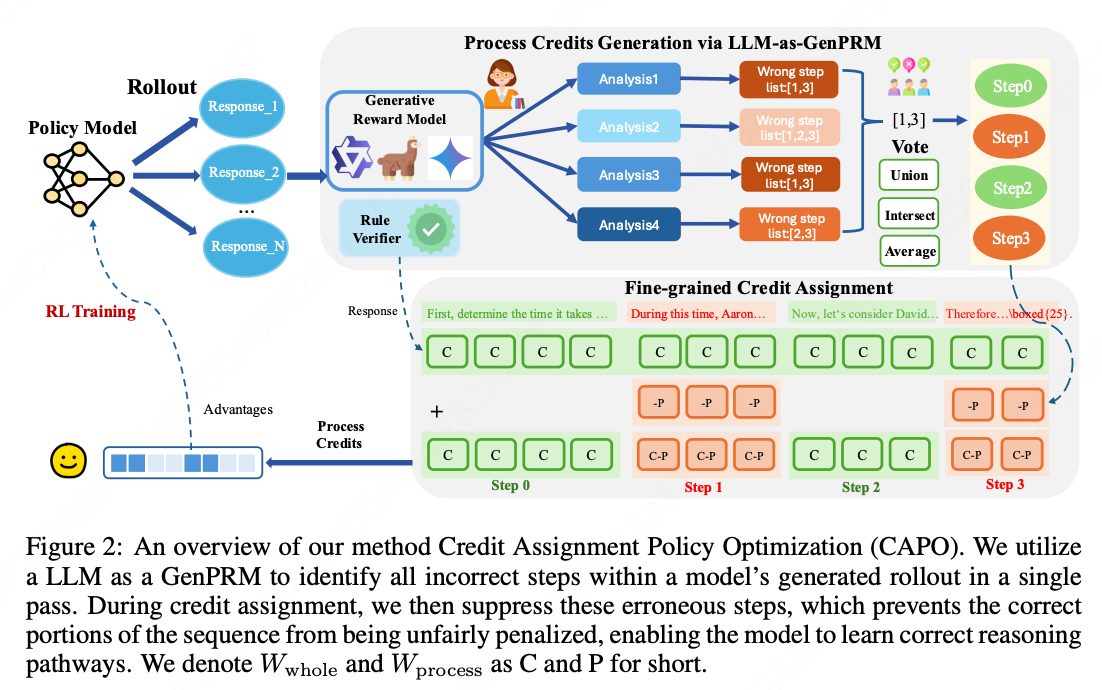
通过LLM-as-GenPRM生成过程评分
1. 从旧策略模型采样n个响应： { y i } i = 1 n ∼ π θ old ( ⋅ ∣ q ) \{y_i\}{i=1}^n \sim \pi{\theta_{\text{old}}}(\cdot|q) {yi}i=1n∼πθold(⋅∣q)
2. 使用LLM-as-GenPRM生成k个批判： { c j } j = 1 k ∼ π LLM-as-GenPRM ( ⋅ ∣ I , q , y i ) \{c_j\}{j=1}^k \sim \pi{\text{LLM-as-GenPRM}}(\cdot|I, q, y_i) {cj}j=1k∼πLLM-as-GenPRM(⋅∣I,q,yi)
3. 提取错误步骤索引： S i , j = ExtractIndices ( c j ) \mathcal{S}_{i,j} = \text{ExtractIndices}(c_j) Si,j=ExtractIndices(cj)
4. 投票机制聚合结果： S i ∗ = ⋂ j = 1 k S i , j \mathcal{S}i^* = \bigcap{j=1}^k \mathcal{S}_{i,j} Si∗=⋂j=1kSi,j
Token级奖励公式（核心）

R t i = r v ⋅ W whole − I ( t ∈ T err i ) ⋅ W process R_t^i = r_v \cdot W_{\text{whole}} - \mathbb{I}(t \in \mathcal{T}{\text{err}}^i) \cdot W{\text{process}} Rti=rv⋅Wwhole−I(t∈Terri)⋅Wprocess

其中：
- r v r_v rv：规则验证器的二元奖励（正确=1，错误=0）
- I ( t ∈ T err i ) \mathbb{I}(t \in \mathcal{T}_{\text{err}}^i) I(t∈Terri)：指示函数，token是否属于错误步骤
- 非对称奖励结构: W whole W_{\text{whole}} Wwhole (整体结果奖励权重) > W process W_{\text{process}} Wprocess (过程惩罚权重)
组相对Token级归一化：
A ^ t i = R t i − mean ( { R t ′ j } ) std ( { R t ′ j } ) \hat{A}t^i = \frac{R_t^i - \text{mean}(\{R{t'}^j\})}{\text{std}(\{R_{t'}^j\})} A^ti=std({Rt′j})Rti−mean({Rt′j})

J CAPO ( θ ) = E q ∼ Q , { y i } ∼ π θ old [ 1 n ∑ i = 1 n 1 L i ∑ t = 1 L i min ⁡ { π θ ( o i , t ∣ q , o i , < t ) π θ old ( o i , t ∣ q , o i , < t ) A ^ t i , clip ( ⋅ , 1 − ϵ , 1 + ϵ ) A ^ t i } ] − β D K L [ π θ ∥ π ref ] J_{\text{CAPO}}(\theta) = \mathbb{E}{q \sim Q, \{y_i\} \sim \pi{\theta_{\text{old}}}} \left[ \frac{1}{n}\sum_{i=1}^n \frac{1}{L_i}\sum_{t=1}^{L_i} \min\left\{ \frac{\pi_\theta(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_{\text{old}}}(o_{i,t}|q,o_{i,<t})}\hat{A}t^i, \text{clip}(\cdot, 1-\epsilon, 1+\epsilon)\hat{A}t^i \right\} \right] - \beta D{KL}[\pi\theta \| \pi_{\text{ref}}] JCAPO(θ)=Eq∼Q,{yi}∼πθold[n1i=1∑nLi1t=1∑Limin{πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t)A^ti,clip(⋅,1−ϵ,1+ϵ)A^ti}]−βDKL[πθ∥πref]

2.6 COPO

核心思想：引入基于结果一致性的全局奖励机制和基于熵的软混合机制，动态平衡局部优势估计与全局优化。

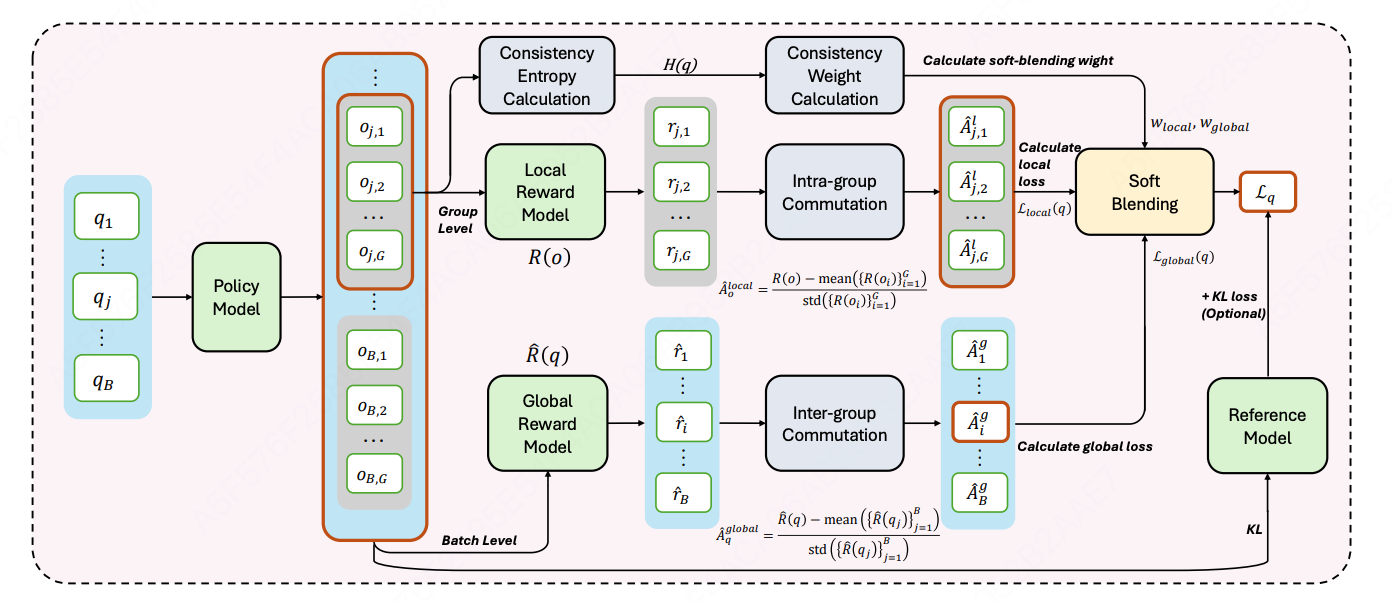
组内局部优化 （针对同一提示词 q q q 下的 G G G 个响应）：局部优势计算和局部优化目标同GRPO，记作 A ^ o i local \hat{A}{o_i}^{\text{local}} A^oilocal、 J local ( θ ) J{\text{local}}(\theta) Jlocal(θ)

组间全局优化（跨不同提示词的一致性学习）

提示词级奖励与优势

R ^ ( q ) = 1 G ∑ i = 1 G r i \hat{R}(q) = \frac{1}{G} \sum_{i=1}^G r_i R^(q)=G1i=1∑Gri

A ^ q global = R ^ ( q j ) − mean ( { R ^ ( q j ) } j = 1 B ) std ( { R ^ ( q j ) } j = 1 B ) , ∀ o i ∈ O q \hat{A}q^{\text{global}} = \frac{\hat{R}(q_j) - \text{mean}(\{\hat{R}(q_j)\}{j=1}^B)}{\text{std}(\{\hat{R}(q_j)\}_{j=1}^B)}, \quad \forall o_i \in \mathcal{O}_q A^qglobal=std({R^(qj)}j=1B)R^(qj)−mean({R^(qj)}j=1B),∀oi∈Oq

其中， B B B 表示改批次中提示词数量。
全局优化目标

J global ( θ ) = E q , { o i } ∼ π θ old [ 1 ∑ i = 1 G ∣ o i ∣ ∑ i = 1 G ∑ t = 1 ∣ o i ∣ min ⁡ ( π θ ( o i , t ∣ q , o i , < t ) π θ old ( o i , t ∣ q , o i , < t ) A ^ q global , clip ( ⋅ ) A ^ q global ) ] J_{\text{global}}(\theta) = \mathbb{E}{q,\{o_i\} \sim \pi{\theta_{\text{old}}}} \left[ \frac{1}{\sum_{i=1}^G |o_i|} \sum_{i=1}^G \sum_{t=1}^{|o_i|} \min\left( \frac{\pi_\theta(o_{i,t} \mid q, o_{i,<t})}{\pi_{\theta_{\text{old}}}(o_{i,t} \mid q, o_{i,<t})} \hat{A}_q^{\text{global}}, \text{clip}(\cdot) \hat{A}_q^{\text{global}} \right) \right] Jglobal(θ)=Eq,{oi}∼πθold ∑i=1G∣oi∣1i=1∑Gt=1∑∣oi∣min(πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t)A^qglobal,clip(⋅)A^qglobal)

熵基软混合机制

一致性熵计算

给定提示词 q q q 的 G G G 个响应，提取唯一结果集合 T q = { τ 1 , τ 2 , ... , τ k } T_q = \{\tau_1, \tau_2, \ldots, \tau_k\} Tq={τ1,τ2,...,τk}：

H ( q ) = − ∑ τ ∈ T q p ( τ ) ⋅ log ⁡ p ( τ ) , p ( τ ) = count ( τ ) G H(q) = -\sum_{\tau \in T_q} p(\tau) \cdot \log p(\tau), \quad p(\tau) = \frac{\text{count}(\tau)}{G} H(q)=−τ∈Tq∑p(τ)⋅logp(τ),p(τ)=Gcount(τ)
- H ( q ) H(q) H(q) 高 → 响应多样性高（模型不确定）
- H ( q ) H(q) H(q) 低 → 响应一致性高（全对或全错）
自适应权重函数

w local ( H ) = σ ( γ ( H − ρ ) ) , w global ( H ) = 1 − w local ( H ) w_{\text{local}}(H) = \sigma(\gamma(H - \rho)), \quad w_{\text{global}}(H) = 1 - w_{\text{local}}(H) wlocal(H)=σ(γ(H−ρ)),wglobal(H)=1−wlocal(H)

混合损失

L q = w local ( H ( q ) ) ⋅ L local ( q ) + w global ( H ( q ) ) ⋅ L global ( q ) \mathcal{L}q = w{\text{local}}(H(q)) \cdot \mathcal{L}{\text{local}}(q) + w{\text{global}}(H(q)) \cdot \mathcal{L}_{\text{global}}(q) Lq=wlocal(H(q))⋅Llocal(q)+wglobal(H(q))⋅Lglobal(q)
- 当一致性熵较高时，表示响应多样性高，局部优化占主导地位，鼓励模型区分并加强组内更高质量的响应。
- 当一致性熵较低时，表示响应一致性高，全局优化占主导地位，推动模型在提示间保持正确性和一致性。

2.7 GTPO 2 ^2 2

核心思想：重塑奖励函数，直接为每个 token 加入基于熵的奖励，让 token 奖励根据熵动态调整，从而准确识别并奖励关键的、高不确定性的决策点。

核心流程

第一步：序列分类

将生成的序列分为两类：
- 成功序列 o i ∈ O + o_i \in O^+ oi∈O+：最终答案正确
- 失败序列 o j ∈ O − o_j \in O^- oj∈O−：最终答案错误
第二步：Token级奖励塑造
1. 成功序列的Token奖励
  
  对于成功序列 o i ∈ O + o_i \in O^+ oi∈O+ 中的任意token o i , t o_{i,t} oi,t：
  
  r ~ i , t + = α 1 r i + α 2 H i , t ∑ k = 1 n H k , t ⋅ d t and r ~ j , t + = 0 \tilde{r}{i,t}^+ = \alpha_1 r_i + \alpha_2 \frac{H{i,t}}{\sum_{k=1}^{n} H_{k,t}} \cdot d_t \quad \text{and} \quad \tilde{r}_{j,t}^+ = 0 r~i,t+=α1ri+α2∑k=1nHk,tHi,t⋅dtandr~j,t+=0
  
  其中， r i = 1 r_i = 1 ri=1， H i , t = − ∑ v ∈ V π θ old ( v ∣ q , o i , < t ) log ⁡ π θ old ( v ∣ q , o i , < t ) H_{i,t} = -\sum_{v \in \mathcal{V}} \pi_{\theta_{\text{old}}}(v \mid q, o_{i,<t}) \log \pi_{\theta_{\text{old}}}(v \mid q, o_{i,<t}) Hi,t=−∑v∈Vπθold(v∣q,oi,<t)logπθold(v∣q,oi,<t) 表示 token生成熵； d t d_t dt 表示长度≥ t t t的成功序列数量（动态缩放因子）
2. 失败序列的Token奖励
  
  对于失败序列 o j ∈ O − o_j \in O^- oj∈O− 中的任意token o j , t o_{j,t} oj,t：
  
  r ~ j , t − = α 1 ⋅ ( − 1 ) + α 2 1 / H j , t ∑ k = 1 m ( 1 / H k , t ) ⋅ h t ⋅ ( − 1 ) and r ~ i , t − = 0 \tilde{r}{j,t}^- = \alpha_1 \cdot (-1) + \alpha_2 \frac{1/H{j,t}}{\sum_{k=1}^{m} (1/H_{k,t})} \cdot h_t \cdot (-1) \quad \text{and} \quad \tilde{r}_{i,t}^- = 0 r~j,t−=α1⋅(−1)+α2∑k=1m(1/Hk,t)1/Hj,t⋅ht⋅(−1)andr~i,t−=0
  
  其中， h t h_t ht 表示长度≥ t t t的失败序列数量。 1 / H j , t 1/H_{j,t} 1/Hj,t 表示逆熵，使用逆熵加权，对低熵（高置信度）的错误token施加更大惩罚，鼓励模型在错误时保持不确定性。
第三步：计算Token级优势

基于塑造后的奖励，分别计算正负序列的优势：

A ~ i , t + = r ~ i , t + − mean ( R ~ + ) std ( R ~ + ) and A ~ j , t − = r ~ j , t − − mean ( R ~ − ) std ( R ~ − ) \tilde{A}{i,t}^+ = \frac{\tilde{r}{i,t}^+ - \text{mean}(\tilde{R}^+)}{\text{std}(\tilde{R}^+)} \quad \text{and} \quad \tilde{A}{j,t}^- = \frac{\tilde{r}{j,t}^- - \text{mean}(\tilde{R}^-)}{\text{std}(\tilde{R}^-)} A~i,t+=std(R~+)r~i,t+−mean(R~+)andA~j,t−=std(R~−)r~j,t−−mean(R~−)
- R ~ + \tilde{R}^+ R~+：批次中所有正序列的token奖励集合
- R ~ − \tilde{R}^- R~−：批次中所有负序列的token奖励集合

目标函数：
J GTPO ( θ ) = E [ 1 ∑ k = 1 G ∣ o k ∣ ( ∑ i = 1 n ∑ t = 1 ∣ o i ∣ min ⁡ ( w i , t ( θ ) A ~ i , t + , clip ( w i , t ( θ ) , 1 − ϵ , 1 + ϵ ) A ~ i , t + ) \mathcal{J}{\text{GTPO}}(\theta) = \mathbb{E}\left[ \frac{1}{\sum{k=1}^{G} |o_k|} \left( \sum_{i=1}^{n} \sum_{t=1}^{|o_i|} \min\left( w_{i,t}(\theta)\tilde{A}{i,t}^+, \text{clip}(w{i,t}(\theta), 1-\epsilon, 1+\epsilon)\tilde{A}_{i,t}^+ \right) \right. \right. JGTPO(θ)=E ∑k=1G∣ok∣1 i=1∑nt=1∑∣oi∣min(wi,t(θ)A~i,t+,clip(wi,t(θ),1−ϵ,1+ϵ)A~i,t+)

∑ j = n + 1 G ∑ t = 1 ∣ o j ∣ min ⁡ ( w j , t ( θ ) A ~ j , t − , clip ( w j , t ( θ ) , 1 − ϵ , 1 + ϵ ) A ~ j , t − ) ) ] \left. \left. + \sum_{j=n+1}^{G} \sum_{t=1}^{|o_j|} \min\left( w_{j,t}(\theta)\tilde{A}{j,t}^-, \text{clip}(w{j,t}(\theta), 1-\epsilon, 1+\epsilon)\tilde{A}_{j,t}^- \right) \right) \right] +j=n+1∑Gt=1∑∣oj∣min(wj,t(θ)A~j,t−,clip(wj,t(θ),1−ϵ,1+ϵ)A~j,t−)

其中重要性采样权重 w i , t ( θ ) = π θ ( o i , t ∣ q , o i , < t ) π θ old ( o i , t ∣ q , o i , < t ) w_{i,t}(\theta) = \frac{\pi_\theta(o_{i,t} \mid q, o_{i,<t})}{\pi_{\theta_{\text{old}}}(o_{i,t} \mid q, o_{i,<t})} wi,t(θ)=πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t)。

2.8 MAPO

核心思想：为不同确定性的样本设计并应用不同的优势函数。

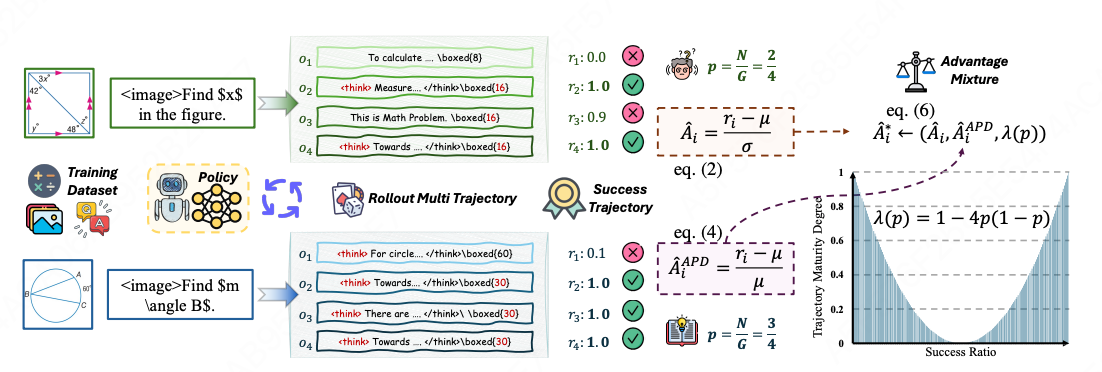
为解决 z-score 在标准差 A ^ i = r i − μ σ \hat{A}_i = \frac{r_i - \mu}{\sigma} A^i=σri−μ 异常小时的不稳定问题，提出优势百分比偏差（Advantage Percent Deviation, APD）：

A ^ i A P D = r i − μ μ \hat{A}_i^{APD} = \frac{r_i - \mu}{\mu} A^iAPD=μri−μ

定义轨迹确定性程度函数：

λ ( p ) = 1 − 4 p ( 1 − p ) ∈ [ 0 , 1 ] ( p ∈ [ 0 , 1 ] ) \lambda(p) = 1 - 4p(1-p) \in [0,1] \quad (p \in [0,1]) λ(p)=1−4p(1−p)∈[0,1](p∈[0,1])

当 p = 0.5 p = 0.5 p=0.5（不确定性最大）： λ ( 0.5 ) = 0 \lambda(0.5) = 0 λ(0.5)=0
当 p = 0 p = 0 p=0 或 p = 1 p = 1 p=1（确定性最高）： λ = 1 \lambda = 1 λ=1

根据轨迹确定性 p p p 动态插值两种优势形式：

A ^ i ∗ = ( 1 − λ ( p ) ) ⋅ r i − μ σ ⏟ Deviation-based + λ ( p ) ⋅ r i − μ μ ⏟ Mean-based \hat{A}i^* = \underbrace{(1-\lambda(p)) \cdot \frac{r_i - \mu}{\sigma}}{\text{Deviation-based}} + \underbrace{\lambda(p) \cdot \frac{r_i - \mu}{\mu}}_{\text{Mean-based}} A^i∗=Deviation-based (1−λ(p))⋅σri−μ+Mean-based λ(p)⋅μri−μ

2.9 NGRPO

核心思想：引入虚拟最大奖励样本，改变群体内奖励的均值和方差，从而为同质化错误样本赋予非零优势，使模型能够从失败中学习并增强探索能力。

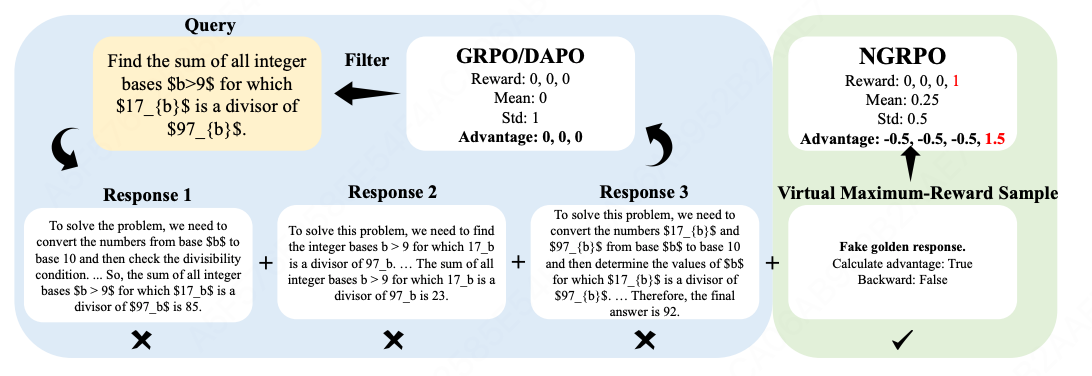
原始奖励集合：
R = { r 1 , ... , r G } \mathcal{R} = \{r_1, \ldots, r_G\} R={r1,...,rG}

增强后的奖励集合（加入虚拟最大奖励样本）：
R ′ = R ∪ { r max ⁡ } \mathcal{R}' = \mathcal{R} \cup \{r_{\max}\} R′=R∪{rmax}

优势函数、均值、标准差：

A i ′ = r i − μ R ′ σ R ′ + ϵ std , μ R ′ = 1 G + 1 ( ( ∑ j = 1 G r j ) + r max ⁡ ) , σ R ′ = 1 G + 1 ∑ r ∈ R ′ ( r − μ R ′ ) 2 A'i = \frac{r_i - \mu'{\mathcal{R}}}{\sigma'{\mathcal{R}} + \epsilon{\text{std}}}, \quad \mu'{\mathcal{R}} = \frac{1}{G+1}\left(\left(\sum{j=1}^{G} r_j\right) + r_{\max}\right), \quad \sigma'{\mathcal{R}} = \sqrt{\frac{1}{G+1}\sum{r \in \mathcal{R}'}(r - \mu'_{\mathcal{R}})^2} Ai′=σR′+ϵstdri−μR′,μR′=G+11((j=1∑Grj)+rmax),σR′=G+11r∈R′∑(r−μR′)2

目标函数：

J N G R P O ( θ ) = E q ∼ P ( Q ) , { o i } i = 1 G ∼ π θ o l d ( o ∣ q ) { 1 G ∑ i = 1 G 1 ∣ o i ∣ ∑ t = 1 ∣ o i ∣ { min ⁡ [ π θ ( o i , t ∣ q , o i , < t ) π θ o l d ( o i , t ∣ q , o i , < t ) A i ′ , clip ( π θ ( o i , t ∣ q , o i , < t ) π θ o l d ( o i , t ∣ q , o i , < t ) , 1 − ϵ , 1 + ϵ ) A i ′ ] } } \mathcal{J}{NGRPO}(\theta) = \mathbb{E}{q \sim P(Q), \{o_i\}{i=1}^{G} \sim \pi{\theta_{old}}(o|q)} \left\{ \frac{1}{G}\sum_{i=1}^{G}\frac{1}{|o_i|}\sum_{t=1}^{|o_i|} \left\{ \min\left[ \frac{\pi_\theta(o_{i,t} \mid q, o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t} \mid q, o_{i,<t})} A'i, \quad \text{clip}\left(\frac{\pi\theta(o_{i,t} \mid q, o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t} \mid q, o_{i,<t})}, 1-\epsilon, 1+\epsilon\right) A'_i \right] \right\} \right\} JNGRPO(θ)=Eq∼P(Q),{oi}i=1G∼πθold(o∣q)⎩ ⎨ ⎧G1i=1∑G∣oi∣1t=1∑∣oi∣{min[πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t)Ai′,clip(πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t),1−ϵ,1+ϵ)Ai′]}⎭ ⎬ ⎫

2.10 GRPO-λ 2 ^2 2

核心思想：将 GAE（广义优势估计）的 λ 加权机制引入无 Critic 的 GRPO 框架，通过重新参数化策略梯度，实现偏差与方差的灵活权衡，从而加速奖励信号在长序列中的传播。

策略梯度重新参数化：将 GAE 从"TD残差之和"转化为"加权累积动作对数概率"，消除对 Critic 网络的依赖。

g ^ = ∑ t = 0 ∞ A GAE ( s t ) ∇ θ log ⁡ π θ ( a t ∣ s t ) = ∑ t = 0 ∞ δ t ∑ l = 0 t ( γ λ ) l ∇ θ log ⁡ π θ ( a t − l ∣ s t − l ) \hat{g} = \sum_{t=0}^{\infty} A_{\text{GAE}}(s_t) \nabla_\theta \log \pi_\theta(a_t|s_t) = \sum_{t=0}^{\infty} \delta_t \sum_{l=0}^{t} (\gamma\lambda)^l \nabla_\theta \log \pi_\theta(a_{t-l}|s_{t-l}) g^=t=0∑∞AGAE(st)∇θlogπθ(at∣st)=t=0∑∞δtl=0∑t(γλ)l∇θlogπθ(at−l∣st−l)

GAE 加权的重要性采样比率

π ratio GAE ( s t ) = exp ⁡ ( ∑ l = 0 t ( γ λ ) l log ⁡ π θ ( a t − l ∣ s t − l ) − ∑ l = 0 t ( γ λ ) l log ⁡ π θ old ( a t − l ∣ s t − l ) ) \pi^{\text{GAE}}{\text{ratio}}(s_t) = \exp\left(\sum{l=0}^{t} (\gamma\lambda)^l \log \pi_\theta(a_{t-l}|s_{t-l}) - \sum_{l=0}^{t} (\gamma\lambda)^l \log \pi_{\theta_{\text{old}}}(a_{t-l}|s_{t-l})\right) πratioGAE(st)=exp(l=0∑t(γλ)llogπθ(at−l∣st−l)−l=0∑t(γλ)llogπθold(at−l∣st−l))
- ( γ λ ) l (\gamma\lambda)^l (γλ)l 为历史动作赋予指数衰减权重，控制信用分配的时域范围。
TD 误差的近似：由于无 Critic 网络，用 GRPO 的组回报估计。
δ t = A NAE = r i − mean ( r ) std ( r ) \delta_t = A_{\text{NAE}} = \frac{r_i - \text{mean}(r)}{\text{std}(r)} δt=ANAE=std(r)ri−mean(r)
目标函数

ℓ π = min ⁡ ( π ratio GAE ( s t ) δ t , clip ( π ratio GAE ( s t ) , 1 − ϵ , 1 + ϵ ) δ t ) \ell_\pi = \min\left(\pi^{\text{GAE}}{\text{ratio}}(s_t)\delta_t,\ \text{clip}\left(\pi^{\text{GAE}}{\text{ratio}}(s_t),\ 1-\epsilon,\ 1+\epsilon\right)\delta_t\right) ℓπ=min(πratioGAE(st)δt, clip(πratioGAE(st), 1−ϵ, 1+ϵ)δt)

2.11 λ-GRPO

核心思想：通过引入可学习参数 λ \lambda λ，将GRPO、DAPO和Dr.GRPO统一为token偏好优化框架，使模型能够根据响应长度分布自适应地学习长/短偏好，而非依赖人工设计的启发式规则。

统一框架
J ( θ ) = 1 ∑ i = 1 G ∣ o i ∣ ∑ i = 1 G f ( o i ) ∑ t = 1 ∣ o i ∣ min ⁡ ( r i , t ( θ ) A ^ i , t , clip ( r i , t ( θ ) , 1 − ϵ , 1 + ϵ ) A ^ i , t ) \mathcal{J}(\theta) = \frac{1}{\sum_{i=1}^{G}|o_i|}\sum_{i=1}^{G}f(o_i)\sum_{t=1}^{|o_i|}\min\left(r_{i,t}(\theta)\hat{A}{i,t}, \text{clip}(r{i,t}(\theta), 1-\epsilon, 1+\epsilon)\hat{A}_{i,t}\right) J(θ)=∑i=1G∣oi∣1i=1∑Gf(oi)t=1∑∣oi∣min(ri,t(θ)A^i,t,clip(ri,t(θ),1−ϵ,1+ϵ)A^i,t)
- μ = 1 G ∑ i = 1 G ∣ o i ∣ \mu = \frac{1}{G}\sum_{i=1}^{G}|o_i| μ=G1∑i=1G∣oi∣ 为平均响应长度。则 f GRPO ( o i ) = μ ∣ o i ∣ f_{\text{GRPO}}(o_i)=\frac{\mu}{|o_i|} fGRPO(oi)=∣oi∣μ、 f DAPO ( o i ) = 1 f_{\text{DAPO}}(o_i) = 1 fDAPO(oi)=1、 f Dr.GRPO ( o i ) = μ f_{\text{Dr.GRPO}}(o_i) = \mu fDr.GRPO(oi)=μ
引入可学习权重
h i = 1 + r ⋅ ∣ o i ∣ − μ σ , g i = h i λ , f λ-GRPO ( o i ) = softmax ( g ) × G h_i = 1 + r\cdot\frac{|o_i|-\mu}{\sigma}, \quad g_i = h_i^{\lambda}, \quad f_{\text{λ-GRPO}}(o_i) = \text{softmax}(g) \times G hi=1+r⋅σ∣oi∣−μ,gi=hiλ,fλ-GRPO(oi)=softmax(g)×G
- λ \lambda λ 控制偏好方向： λ < 0 \lambda < 0 λ<0：偏好短响应； λ = 0 \lambda = 0 λ=0：长度中性（等价于DAPO）； λ > 0 \lambda > 0 λ>0：偏好长响应

2.12 FAPO

核心思想：以生成式奖励模型检测flawed positives，通过无参数惩罚机制实现"早期利用-后期抑制"的自适应阶段转换，兼顾训练效率与推理可靠性。

生成式奖励模型（GenRM）训练

Flawed Positive（缺陷正样本，即答案正确但推理有缺陷）的双重效应：早期作为"垫脚石"加速能力提升；后期固化不可靠推理模式，限制性能上限。为准确检测flawed positives，训练一个生成式奖励模型，采用步骤级RL奖励：

R F A P O - G e n R M = R O u t c o m e ∗ R P r o c e s s R_{FAPO\text{-}GenRM} = R_{Outcome} * R_{Process} RFAPO-GenRM=ROutcome∗RProcess

R O u t c o m e = { 1 , if y ^ θ = y ∗ − 1 , otherwise , R P r o c e s s = { − ∣ t ^ θ − t ∗ ∣ n , if y ^ θ = y ∗ = F P 0 , otherwise R_{Outcome} = \begin{cases} 1, & \text{if } \hat{y}\theta = y^* \\ -1, & \text{otherwise} \end{cases}, \quad R{Process} = \begin{cases} -\frac{|\hat{t}\theta - t^*|}{n}, & \text{if } \hat{y}\theta = y^* = FP \\ 0, & \text{otherwise} \end{cases} ROutcome={1,−1,if y^θ=y∗otherwise,RProcess={−n∣t^θ−t∗∣,0,if y^θ=y∗=FPotherwise
- t ^ θ , t ∗ \hat{t}_\theta, t^* t^θ,t∗：预测与真实错误位置索引
- n n n：总步骤数，确保 R P r o c e s s ∈ [ − 1 , 0 ] R_{Process} \in [-1, 0] RProcess∈[−1,0]
- 距离敏感惩罚：预测错误位置越接近真实位置，惩罚越轻。
缺陷感知奖励惩罚机制

将训练好的GenRM集成到GRPO中，对flawed positives施加无参数惩罚：

R F A P O ( o , a ∗ ∣ θ ) = R R L V R ( o , a ∗ ) + R Δ ( o , a ∗ ∣ θ ) R_{FAPO}(o, a^*|\theta) = R_{RLVR}(o, a^*) + R_\Delta(o, a^*|\theta) RFAPO(o,a∗∣θ)=RRLVR(o,a∗)+RΔ(o,a∗∣θ)

其中惩罚项：
R Δ ( o , a ∗ ∣ θ ) = { − λ , if I ( o , a ∗ ) and y ^ θ ( o , a ∗ ) = F P 0 , otherwise R_\Delta(o, a^*|\theta) = \begin{cases} -\lambda, & \text{if } \mathcal{I}(o, a^*) \text{ and } \hat{y}_\theta(o, a^*) = FP \\ 0, & \text{otherwise} \end{cases} RΔ(o,a∗∣θ)={−λ,0,if I(o,a∗) and y^θ(o,a∗)=FPotherwise

自适应阶段转换 :设当前rollout中完全正确样本比例为 α \alpha α，负样本比例为 β \beta β，定义学习进度 ρ = α / β \rho = \alpha/\beta ρ=α/β。采用多数引导策略 ：取 λ = 1 \lambda = 1 λ=1（默认），当 α > β \alpha > \beta α>β 时自然触发阶段转换（Warn-up -> Refinement）。

2.13 SAPO

核心思想：用平滑的衰减替代硬性的截断，用自适应的权重平衡探索与利用。

软门控机制（Soft Gating）：利用以温度系数控制的 Sigmoid 函数替代传统的硬截断，构建连续的信任区域，在偏离策略时平滑衰减梯度而非直接置零。
非对称温度控制（Asymmetric Temperatures）：针对正负优势（Advantage）样本对训练稳定性的不同影响，对负样本采用更高的温度系数使其梯度衰减更快，从而抑制大词表下的噪声扩散。

目标函数：
J S A P O ( θ ) = E q ∼ D , { y i } i = 1 G ∼ π θ old ( ⋅ ∣ q ) [ 1 G ∑ i = 1 G 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ f i , t ( r i , t ( θ ) ) A ^ i , t ] \mathcal{J}{SAPO}(\theta) = \mathbb{E}{q \sim \mathcal{D}, \{y_i\}{i=1}^G \sim \pi{\theta_{\text{old}}}(\cdot|q)} \left[ \frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} f_{i,t}(r_{i,t}(\theta)) \hat{A}_{i,t} \right] JSAPO(θ)=Eq∼D,{yi}i=1G∼πθold(⋅∣q) G1i=1∑G∣yi∣1t=1∑∣yi∣fi,t(ri,t(θ))A^i,t

软门控函数：

f i , t ( x ) = σ ( τ i , t ( x − 1 ) ) ⋅ 4 τ i , t f_{i,t}(x) = \sigma(\tau_{i,t}(x-1)) \cdot \frac{4}{\tau_{i,t}} fi,t(x)=σ(τi,t(x−1))⋅τi,t4

温度参数（非对称设计）：
τ i , t = { τ pos , if A ^ i , t > 0 τ neg , otherwise , τ neg > τ pos \tau_{i,t} = \begin{cases} \tau_{\text{pos}}, & \text{if } \hat{A}{i,t} > 0 \\ \tau{\text{neg}}, & \text{otherwise} \end{cases}, \quad \tau_{\text{neg}} > \tau_{\text{pos}} τi,t={τpos,τneg,if A^i,t>0otherwise,τneg>τpos

GRPO 算法演进——奖励设计篇

文章目录

一、引言

二、奖励设计篇

2.1 S-GRPO

2.2 SEED-GRPO

2.3 GRPO-λ 1 ^1 1

2.4 EDGE-GRPO

2.5 CAPO

2.6 COPO

2.7 GTPO 2 ^2 2

2.8 MAPO

2.9 NGRPO

2.10 GRPO-λ 2 ^2 2

2.11 λ-GRPO

2.12 FAPO

2.13 SAPO

三、相关文章