文章目录
- 一、引言
- 二、裁剪机制篇
-
- [2.1 DAPO](#2.1 DAPO)
- [2.2 DCPO](#2.2 DCPO)
- [2.3 ASPO](#2.3 ASPO)
- [2.4 BAPO](#2.4 BAPO)
- [2.5 ABC-GRPO](#2.5 ABC-GRPO)
- 三、相关文章
一、引言
Group Relative Policy Optimization(GRPO)作为大语言模型强化学习的核心算法之一,通过组内相对优势估计消除了对价值网络的依赖,显著降低了训练成本。然而,随着推理任务复杂度的提升,GRPO 在长链推理场景下暴露出熵崩溃、训练不稳定、探索效率低等关键问题。
针对这些挑战,研究者们围绕裁剪机制这一核心组件展开了深入探索。裁剪机制通过约束策略更新幅度来平衡稳定性与探索性,但传统的对称裁剪难以适应不同概率区域和优势符号的复杂需求 。从 DAPO 的解耦裁剪边界,到 DCPO 的动态自适应裁剪,再到 ASPO 的权重翻转与 BAPO 的批级动态边界优化,乃至 ABC-GRPO 的四边界非对称设计,这一系列工作逐步构建起一套精细化、自适应、场景感知的裁剪优化体系。
本文深入剖析 GRPO 裁剪机制演进的五大代表性方法(DAPO、DCPO、ASPO、BAPO、ABC-GRPO)的核心思想、数学原理与设计权衡。
| 算法名称 | 发布时间 | 算法完整名称 | 论文链接 |
|---|---|---|---|
| DAPO | 2025.03 | Decoupled Clip and Dynamic sAmpling Policy Optimization | https://arxiv.org/abs/2503.14476 |
| DCPO | 2025.09 | Dynamic Clipping Policy Optimization | https://arxiv.org/abs/2509.02333 |
| ASPO | 2025.10 | Asymmetric Importance Sampling Policy Optimization | https://arxiv.org/abs/2510.06062 |
| BAPO | 2025.10 | BAlanced Policy Optimization with Adaptive Clipping | https://arxiv.org/abs/2510.18927 |
| ABC-GRPO | 2026.01 | Adaptive-Boundary-Clipping Group Relative Policy Optimization | https://arxiv.org/abs/2601.03895 |
二、裁剪机制篇
2.1 DAPO
核心思想:通过"解耦裁剪上下限 + 动态过滤样本 + Token级损失 + 软长度惩罚"四大创新,解决了 GRPO 在长链推理任务中的熵崩溃和训练不稳定问题,实现了更高效的探索与更稳定的收敛。
J DAPO ( θ ) = E ( q , a ) ∼ D , { o i } i = 1 G ∼ π θ old ( ⋅ ∣ q ) [ 1 ∑ i = 1 G ∣ o i ∣ ∑ i = 1 G ∑ t = 1 ∣ o i ∣ min ( r i , t ( θ ) A ^ i , t , clip ( r i , t ( θ ) , 1 − ϵ low , 1 + ϵ high ) A ^ i , t ) ] s.t. 0 < ∣ { o i ∣ is_equivalent ( a , o i ) } ∣ < G \mathcal{J}{\text{DAPO}}(\theta) = \mathbb{E}{(q,a) \sim \mathcal{D}, \{o_i\}{i=1}^G \sim \pi{\theta_{\text{old}}}(\cdot | q)} \left[ \textcolor{red}{\frac{1}{\sum_{i=1}^G |o_i|} \sum_{i=1}^G} \sum_{t=1}^{|o_i|} \min \left( r_{i,t}(\theta) \hat{A}{i,t}, \text{clip}\left(r{i,t}(\theta), 1 - \textcolor{red}{\epsilon_{\text{low}}}, 1 + \textcolor{red}{\epsilon_{\text{high}}}\right) \hat{A}_{i,t} \right) \right]\\ \textcolor{red}{\text{s.t. } 0 < \left| \{o_i \mid \text{is\_equivalent}(a, o_i)\} \right| < G} JDAPO(θ)=E(q,a)∼D,{oi}i=1G∼πθold(⋅∣q) ∑i=1G∣oi∣1i=1∑Gt=1∑∣oi∣min(ri,t(θ)A^i,t,clip(ri,t(θ),1−ϵlow,1+ϵhigh)A^i,t) s.t. 0< {oi∣is_equivalent(a,oi)} <G
详见:深度解析 DAPO:从 GRPO 到 Decoupled Clip & Dynamic Sampling
2.2 DCPO
核心思想:通过动态自适应裁剪(DAC)+ 平滑优势标准化(SAS)+ Only Token Mean 损失函数(OTM Loss)三层设计平衡稳定性与探索性。
-
动态自适应裁剪(Dynamic-Adaptive Clipping, DAC)
重要性采样的方差(旧策略概率 q ( x ) q(x) q(x)、新策略概率 p ( x ) p(x) p(x)、重要性比率 r ( x ) r(x) r(x)):
Var x ∼ q [ f ( x ) p ( x ) q ( x ) ] − Var x ∼ p [ f ( x ) ] = E x ∼ p [ f ( x ) 2 ( p ( x ) q ( x ) − 1 ) ] \text{Var}{x \sim q}\left[f(x)\frac{p(x)}{q(x)}\right] - \text{Var}{x \sim p}[f(x)] = \mathbb{E}_{x \sim p}\left[f(x)^2\left(\frac{p(x)}{q(x)} - 1\right)\right] Varx∼q[f(x)q(x)p(x)]−Varx∼p[f(x)]=Ex∼p[f(x)2(q(x)p(x)−1)]为控制方差-偏差权衡,在原先约束 ∣ ( r ( x ) − 1 ) ∣ ≤ ϵ |(r(x) - 1)| \leq \epsilon ∣(r(x)−1)∣≤ϵ 基础上施加概率相关约束,修改为:
∣ ( r ( x ) − 1 ) p ( x ) ∣ ≤ ϵ |(r(x) - 1)p(x)| \leq \epsilon ∣(r(x)−1)p(x)∣≤ϵ代入 p ( x ) = r ( x ) q ( x ) p(x) = r(x)q(x) p(x)=r(x)q(x) 并求解,得到闭式解:
0.5 + 1 2 max ( 1 − 4 ϵ low q ( x ) , 0 ) ≤ r ( x ) ≤ 0.5 + 1 2 1 + 4 ϵ high q ( x ) 0.5 + \frac{1}{2}\sqrt{\max\left(1 - \frac{4\epsilon_{\text{low}}}{q(x)}, 0\right)} \leq r(x) \leq 0.5 + \frac{1}{2}\sqrt{1 + \frac{4\epsilon_{\text{high}}}{q(x)}} 0.5+21max(1−q(x)4ϵlow,0) ≤r(x)≤0.5+211+q(x)4ϵhigh
从而使得低概率区域( q ( x ) q(x) q(x) 小)获得更宽裁剪边界,拥有更大探索空间。
-
平滑优势标准化(Smooth Advantage Standardization, SAS)
累积标准化(统计量基于同一提示的所有历史响应 ):
A ^ total , j i = ( R j i − μ total i ) σ total i \hat{A}{\text{total},j}^i = \frac{(R_j^i - \mu{\text{total}}^i)}{\sigma_{\text{total}}^i} A^total,ji=σtotali(Rji−μtotali)为缓解步级标准化 A ^ new , j i \hat{A}{\text{new},j}^i A^new,ji 和累积标准化 A ^ total , j i \hat{A}{\text{total},j}^i A^total,ji 的波动,引入平滑函数:
S A ^ new , j i = i − 1 i A ^ new , j i + 1 i A ^ total , j i , S A ^ total , j i = 1 i A ^ new , j i + i − 1 i A ^ total , j i \hat{SA}{\text{new},j}^i = \frac{i-1}{i}\hat{A}{\text{new},j}^i + \frac{1}{i}\hat{A}{\text{total},j}^i, \quad \hat{SA}{\text{total},j}^i = \frac{1}{i}\hat{A}{\text{new},j}^i + \frac{i-1}{i}\hat{A}{\text{total},j}^i SA^new,ji=ii−1A^new,ji+i1A^total,ji,SA^total,ji=i1A^new,ji+ii−1A^total,ji
最终选择绝对值较小的平滑优势,减少波动影响:
A ^ j i = { S A ^ new , j i , when ∣ S A ^ new , j i ∣ < ∣ S A ^ total , j i ∣ S A ^ total , j i , otherwise \hat{A}j^i = \begin{cases} \hat{SA}{\text{new},j}^i, & \text{when } |\hat{SA}{\text{new},j}^i| < |\hat{SA}{\text{total},j}^i| \\ \hat{SA}_{\text{total},j}^i, & \text{otherwise} \end{cases} A^ji={SA^new,ji,SA^total,ji,when ∣SA^new,ji∣<∣SA^total,ji∣otherwise
-
OTM损失(Only Token Mean Loss)
J DCPO ( θ ) = ∑ i = 1 G 1 ∣ o i ∣ ∑ t = 1 ∣ o i ∣ min ( r i , t ( θ ) A ^ i , t , clip ( r i , t ( θ ) , 1 − ε low , 1 + ε high ) A ^ i , t ) \mathcal{J}{\text{DCPO}}(\theta) = \textcolor{red}{\sum{i=1}^G \frac{1}{|o_i|} \sum_{t=1}^{|o_i|}}\min\left(r_{i,t}(\theta)\hat{A}{i,t}, \text{clip}\left(r{i,t}(\theta), 1-\varepsilon_{\text{low}}, 1+\varepsilon_{\text{high}}\right)\hat{A}_{i,t}\right) JDCPO(θ)=i=1∑G∣oi∣1t=1∑∣oi∣min(ri,t(θ)A^i,t,clip(ri,t(θ),1−εlow,1+εhigh)A^i,t)
2.3 ASPO
核心思想:翻转正样本权重,将正优势token的重要性采样权重取倒数,让低概率token得到更强的更新,而高概率token被适当削弱。
核心流程
-
Step 1: Token Masking(硬裁剪)
梯度被屏蔽的条件(保留GRPO原始裁剪机制):
- r t i ( θ ) < 1 − ε low r_t^i(\theta) < 1 - \varepsilon_{\text{low}} rti(θ)<1−εlow 且 A ^ t i < 0 \hat{A}_t^i < 0 A^ti<0(负优势且比率过低)
- r t i ( θ ) > 1 + ε high r_t^i(\theta) > 1 + \varepsilon_{\text{high}} rti(θ)>1+εhigh 且 A ^ t i > 0 \hat{A}_t^i > 0 A^ti>0(正优势且比率过高)
-
Step 2:Weight Flipping(权重翻转)
-
负样本(Â < 0) :保持GRPO原始比率
r ^ t i = r t i \hat{r}_t^i = r_t^i r^ti=rti -
正样本(Â > 0) :使用翻转权重
r ^ t i = π θ old ( o t i ∣ q , o < t i ) π θ ( o t i ∣ q , o < t i ) sg ( π θ 2 ( o t i ∣ q , o < t i ) ) \hat{r}t^i = \frac{\pi{\theta_{\text{old}}}(o_t^i \mid q, o_{<t}^i) \pi_\theta(o_t^i \mid q, o_{<t}^i)}{\text{sg}(\pi_\theta^2(o_t^i \mid q, o_{<t}^i))} r^ti=sg(πθ2(oti∣q,o<ti))πθold(oti∣q,o<ti)πθ(oti∣q,o<ti)其中, sg ( ⋅ ) \text{sg}(\cdot) sg(⋅) 表示 Stop Gradient操作(阻止梯度流经分母)。
简化理解: r ^ t i ≈ π θ old π θ = 1 r t i \text{简化理解:}\hat{r}t^i \approx \frac{\pi{\theta_{\text{old}}}}{\pi_\theta} = \frac{1}{r_t^i} 简化理解:r^ti≈πθπθold=rti1- 原始GRPO(正样本): r = π θ π θ old > 1 r = \frac{\pi_\theta}{\pi_{\theta_{\text{old}}}} > 1 r=πθoldπθ>1 → 高概率token获得高权重(加剧优势)
- ASPO(正样本翻转): r ^ ≈ π θ old π θ r̂ ≈ \frac{\pi_{\theta_{\text{old}}}}{\pi_\theta} r^≈πθπθold → 低概率token获得高权重(纠正偏差)
-
-
Step 3:Dual Clipping(双裁剪)
- 权重翻转后,正样本区域的极端情况(原Â>0区域的lower部分)需要额外处理。
- 使用软裁剪方式:裁剪数值,保留梯度
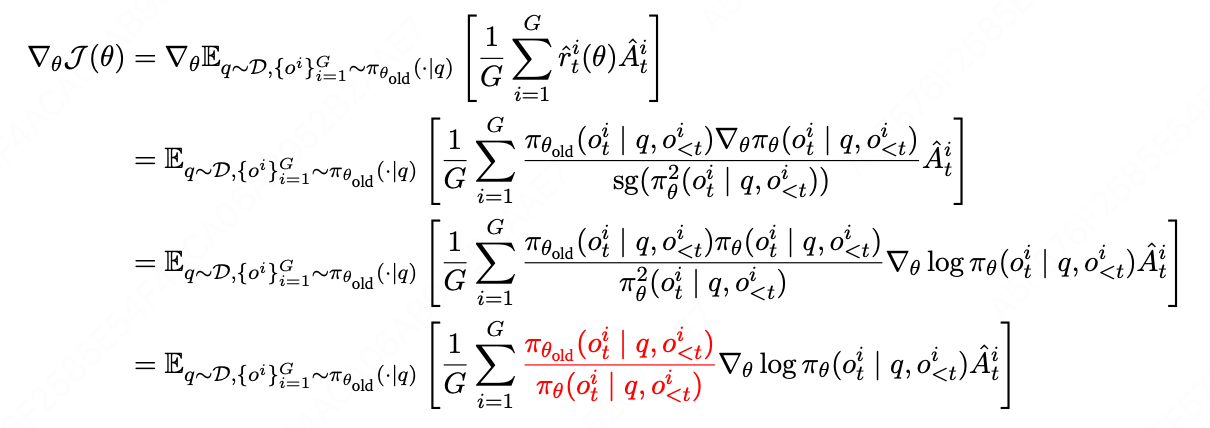
2.4 BAPO
核心思想: 为每一批数据动态地寻找最优的裁剪边界。确保正优势 token 对策略梯度总损失的贡献不低于一个预设的目标比例。
- 核心约束条件:强制正token贡献占比 ≥ ρ 0 \rho_0 ρ0,防止负样本主导
∣ ∑ A t > 0 π θ rollout ( y t ) ⋅ [ min ( r t ⋅ A t , clip ( r t , 0 , c high ) ⋅ A t ) ] ∣ ∣ ∑ A t π θ rollout ( y t ) ⋅ [ min ( r t ⋅ A t , clip ( r t , c low , c high ) ⋅ A t ) ] ∣ ≥ ρ 0 \frac{\left| \sum_{A_t > 0} \pi_{\theta_{\text{rollout}}}(y_t) \cdot \left[ \min(r_t \cdot A_t, \text{clip}(r_t, 0, c_{\text{high}}) \cdot A_t) \right] \right|}{\left| \sum_{A_t} \pi_{\theta_{\text{rollout}}}(y_t) \cdot \left[ \min(r_t \cdot A_t, \text{clip}(r_t, c_{\text{low}}, c_{\text{high}}) \cdot A_t) \right] \right|} \geq \rho_0 ∑Atπθrollout(yt)⋅[min(rt⋅At,clip(rt,clow,chigh)⋅At)] ∑At>0πθrollout(yt)⋅[min(rt⋅At,clip(rt,0,chigh)⋅At)] ≥ρ0
- 动态边界调整策略:

2.5 ABC-GRPO
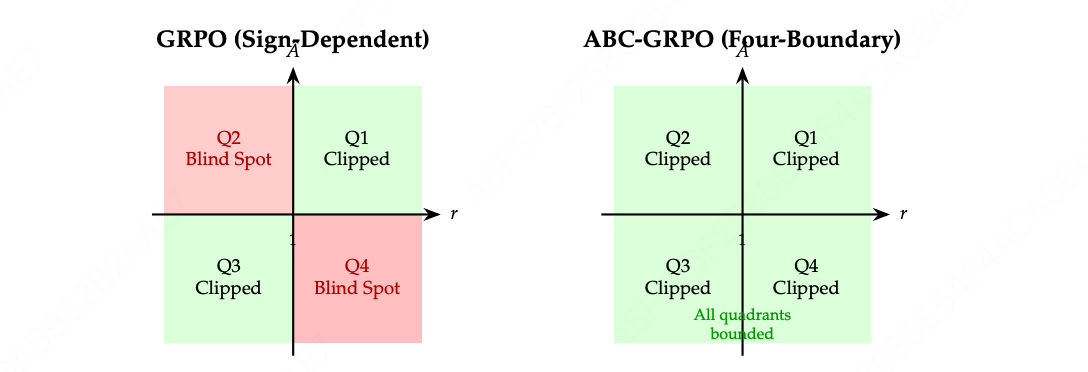
核心思想:引入非对称自适应边界裁剪机制,使用四个独立的剪切边界(ε1~ε4),替代GRPO中仅依赖于两个条件边界的剪切操作,从而消除了GRPO (r, A)坐标系中Q4和Q2象限的盲点,避免了不受限制的梯度更新。
-
四边界裁剪函数:
r ~ i , t = { clip ( r i , t , 1 − ε 2 , 1 + ε 1 ) , if A ^ i > 0 clip ( r i , t , 1 − ε 4 , 1 + ε 3 ) , if A ^ i ≤ 0 \tilde{r}{i,t} = \begin{cases} \text{clip}(r{i,t}, 1-\varepsilon_2, 1+\varepsilon_1), & \text{if } \hat{A}i > 0 \\ \text{clip}(r{i,t}, 1-\varepsilon_4, 1+\varepsilon_3), & \text{if } \hat{A}_i \leq 0 \end{cases} r~i,t={clip(ri,t,1−ε2,1+ε1),clip(ri,t,1−ε4,1+ε3),if A^i>0if A^i≤0
参数 控制象限 边界类型 ε 1 \varepsilon_1 ε1 Q1 (Â>0, r>1) 正优势上界 ε 2 \varepsilon_2 ε2 Q2 (Â>0, r<1) 正优势下界(新增) ε 3 \varepsilon_3 ε3 Q4 (Â≤0, r>1) 负优势上界(新增) ε 4 \varepsilon_4 ε4 Q3 (Â≤0, r<1) 负优势下界 -
四边界 vs 两边界:
场景 GRPO问题 ABC-GRPO解决 正优势+低概率比 (Q2) 可能过度惩罚低概率token ε₂控制下界,防止过度抑制 负优势+高概率比 (Q4) 可能过度更新高概率token ε₃控制上界,防止过度鼓励