Z算法（线性时间模式搜索算法）

在许多涉及字符串的编程问题中，我们通常需要在文本中寻找某种模式的出现。一种经典方法如朴素字符串匹配算法在文本的每个索引处检查图案，导致时间复杂度为O（n·m），其中n是文本长度，m是模式长度。对于大量输入来说，这种方式效率较低。

为此，存在几种高效的字符串匹配算法，其中之一是Z算法，它允许我们在线性时间内进行模式匹配。这意味着它能在 O（n + m）时间内找到所有匹配。

什么是Z阵列？

Z阵列的计算

Z阵列在模式匹配中的作用

Z算法的优势

现实应用

相关问题

什么是Z阵列？

Z算法围绕计算一种叫做Z阵列的东西展开。

假设我们有一串长度为n的字符串s。

Z-数组 Z[0...n-1] 对于每个索引 i，存储从 i 起且也是字符串 s 前缀的最长子串长度。

简单来说：

Z[i] 告诉我们从位置 i 开始有多少字符与字符串开头匹配。

在进入Z阵列构造之前，先举一个小例子来更好地理解这一点。

示例：

s = "aabxaab"。

Z[0] = 0 // by definition; we don't compare the full string with itself

现在，我们计算索引1到6的剩余值。

Z[1] = 1 → 只有第一个字符"a"与前缀匹配。

Z[2] = 0 → 'b' 与前缀 'a' 的第一个字符不匹配。

Z[3] = 0 → 'x' 与前缀 'a' 的第一个字符不匹配。

Z[4] = 3 → 子串"aab"与前缀"aab"匹配。

Z[5] = 1 → 只有"a"与前缀的第一个字符匹配。

Z[6] = 0 → 'b' 与前缀 'a' 的第一个字符不匹配。

最终Z阵列

z[] = [0, 1, 0, 0, 3, 1, 0]

Z阵列的计算

计算Z数组检查的简单方法是，对于每个索引i，s[i...]中的字符数与s[0]开头的前缀相符。这在最坏情况下可能导致O（n²）时间。

然而，使用Z算法，我们可以在O（n）时间内计算所有Z[i]值。

在计算Z数组时，我们维护一个窗口[l， r]，称为Z盒，表示与字符串前缀匹配的最右侧子串。

l 是当前 Z 盒的起始索引（前缀匹配的起点）。

r 是结尾索引（与前缀最远的位置）。

具体来说，s[l...r] 匹配 s[0...（r - l）]。

该窗口帮助我们重用之前的计算以优化Z阵列的构建。

为什么Z-box有用？

处理索引i时，有两种可能：

如果我>r（Z框外）：

=>开始比较前缀和以i开头的子串。

=> 统计匹配字符的数量，并将此长度存储在Z[i]中。

=> 更新窗口 [L， R] 以表示这个新的匹配段。

如果 i ≤ r：

=> 设 k 是前缀中对应于 i 的位置（k = i - L）。

=> 使用值 Z[k] 作为参考。

-> 如果 Z[k] 严格小于 [L， R] 剩余长度，则赋值 Z[i] = Z[k]。

-> 否则，开始比较当前窗口以外的角色以延长匹配。

=> 扩展后，如果找到更长的匹配，则更新窗口 [L， R]。

复制代码

import java.util.ArrayList;
import java.util.Arrays;

public class GfG {
    public static ArrayList<Integer> zFunction(String s) {
        int n = s.length();
        ArrayList<Integer> z = new ArrayList<>(n);
        for (int i = 0; i < n; i++) {
            z.add(0);
        }
        int l = 0, r = 0;

        for (int i = 1; i < n; i++) {
            if (i <= r) {
                int k = i - l;
                
                // Case 2: reuse the previously computed value
                z.set(i, Math.min(r - i + 1, z.get(k)));
            }

            // Try to extend the Z-box beyond r
            while (i + z.get(i) < n &&
                s.charAt(z.get(i)) == s.charAt(i + z.get(i))) {
                z.set(i, z.get(i) + 1);
            }

            // Update the [l, r] window if extended
            if (i + z.get(i) - 1 > r) {
                l = i;
                r = i + z.get(i) - 1;
            }
        }
        return z;
    }

    public static void main(String[] args) {
        String s = "aabxaab";
        
        ArrayList<Integer> z = zFunction(s);
        
        for (int x : z) {
            System.out.print(x + " ");
        }
    }
}

输出

0 1 0 0 3 1 0

时间复杂度：O（n）

辅助空间：O（n）

为什么这在线性时间内有效

线性时间复杂度的关键在于，每次进行字符比较（手动匹配）时，我们都会扩展Z盒的右端。

由于r只向前移动，从不向后移动，此类比较的总数最多为n。

Z阵列在模式匹配中的作用

给定两个字符串：文本（文本）和模式（模式），由小写英文字母表组成，找到所有以0为基础的起始索引，其中模式作为文本中的子字符串出现。

示例：

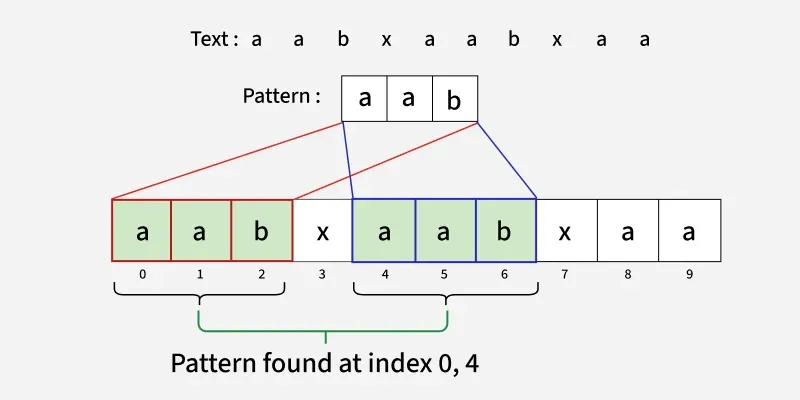
输入：文本 = "aabxaabxaa"，模式 = "aab"

输出：[0， 4]

解释：

KMP模式搜索算法

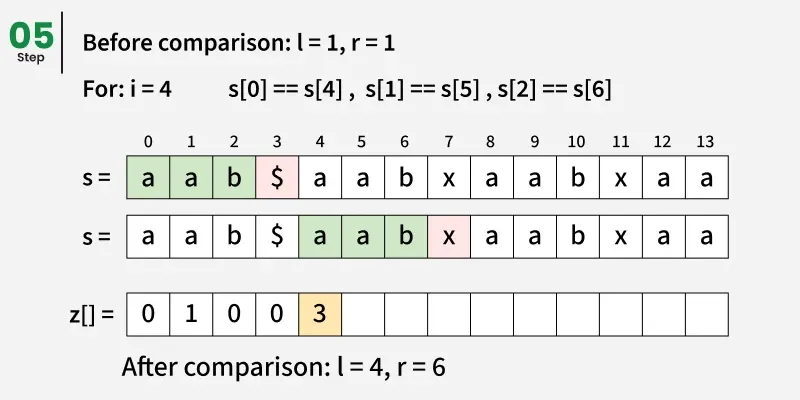
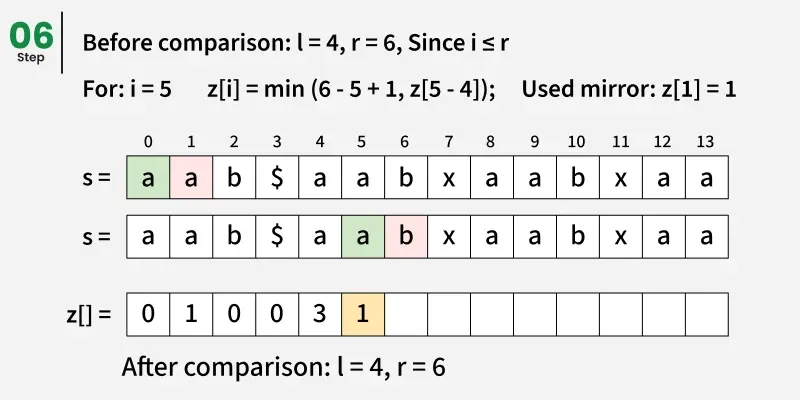
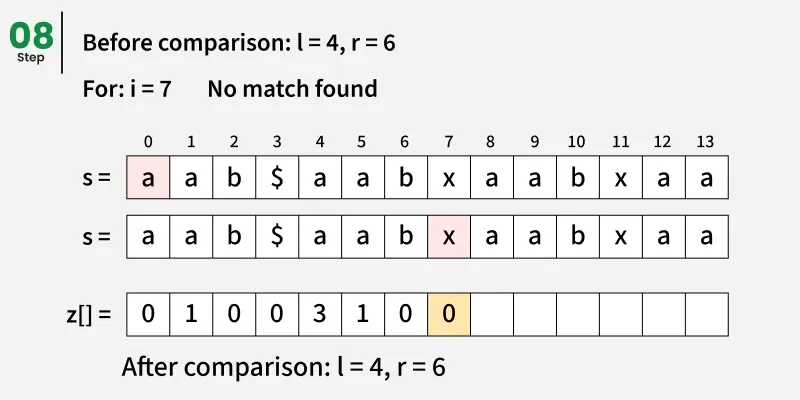
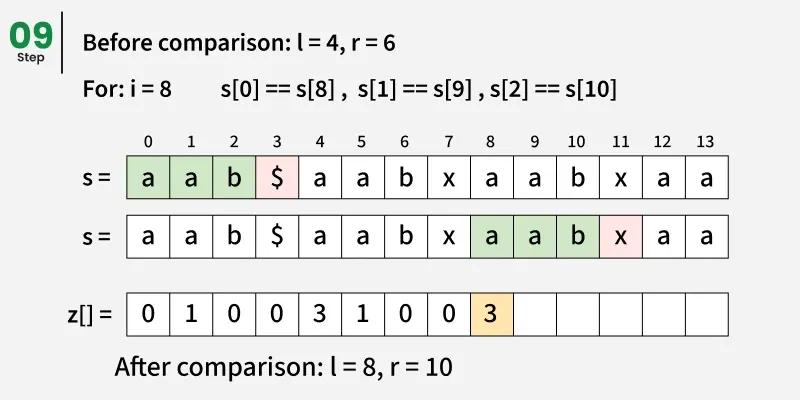
关键思想是预处理一个由模式和文本结合形成的新字符串，该字符串之间用一个特殊的分隔符（例如，）分隔，该分隔符在任何字符串中都不存在。这样可以避免意外的重叠。我们构造一个新字符串如下： s = p a t t e r n + ′ ）分隔，该分隔符在任何字符串中都不存在。这样可以避免意外的重叠。我们构造一个新字符串如下： s = pattern + ' ）分隔，该分隔符在任何字符串中都不存在。这样可以避免意外的重叠。我们构造一个新字符串如下：s=pattern+′' + text

然后我们计算该组合字符串的Z-数组。

任意位置 i 的 Z 数组告诉我们，与该位置起始文本子串匹配的最长前缀长度（根据图案和分隔符调整偏移量）。

因此，每当我们找到一个位置i使得：

Z[i] == length of pattern

这意味着整个图案在某一位置与文本相匹配：

match position = i - (pattern length + 1)

插图：

复制代码

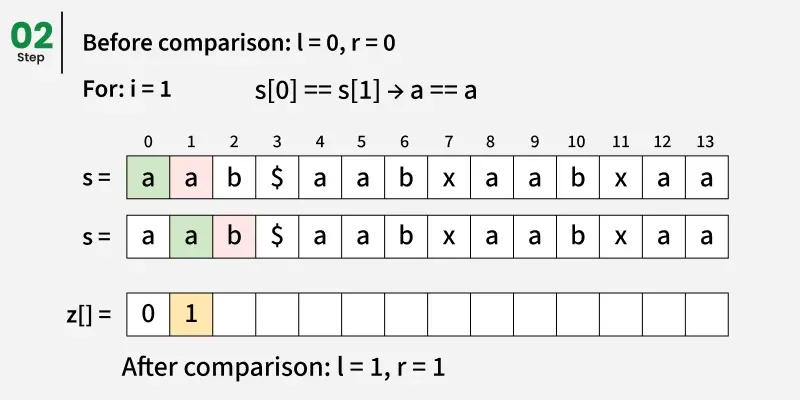
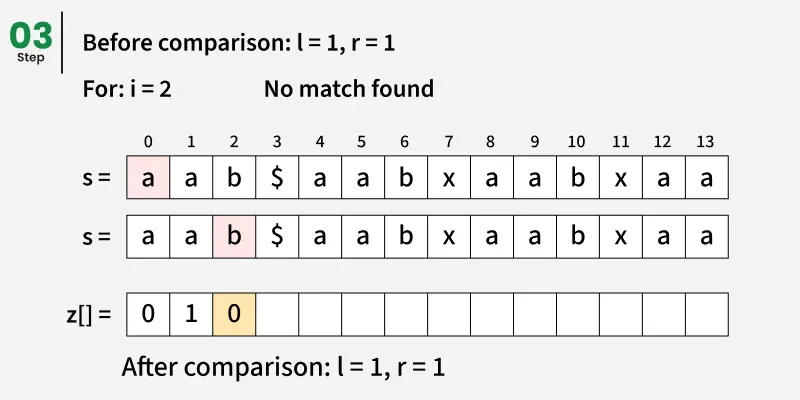
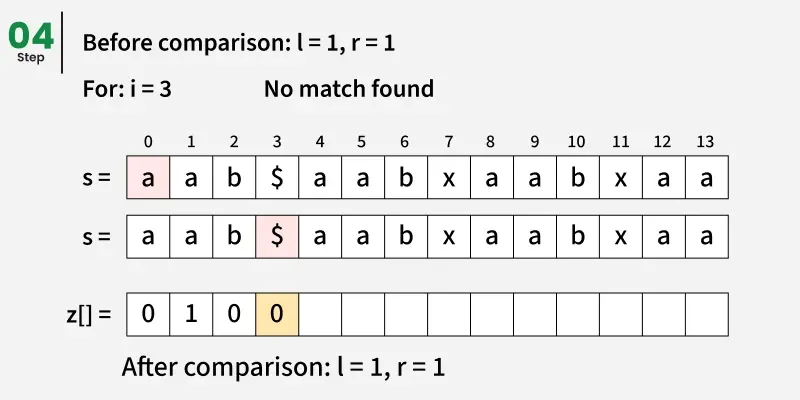
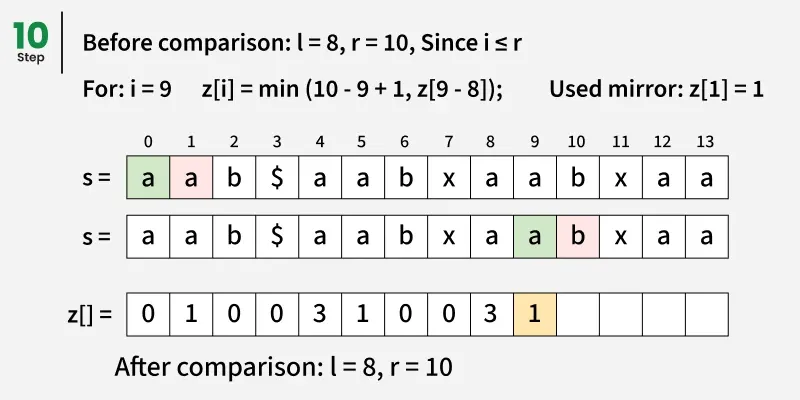
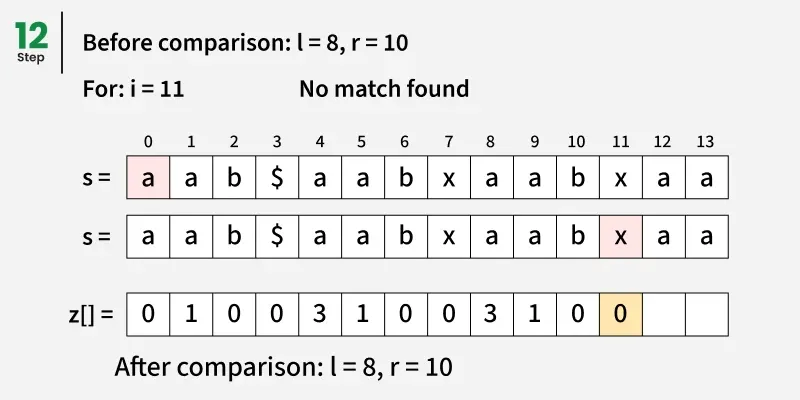
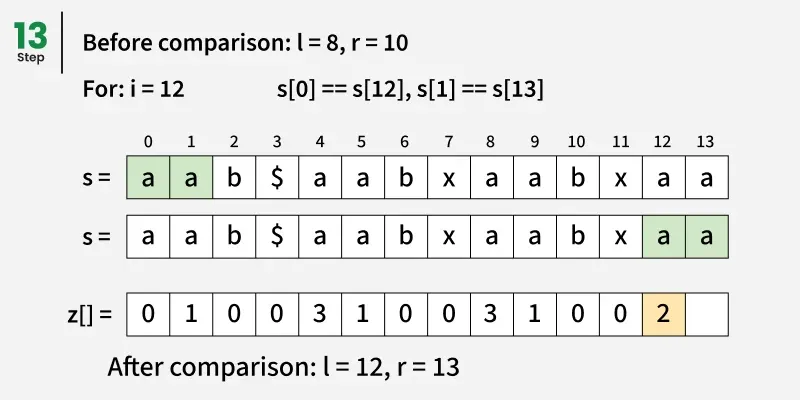
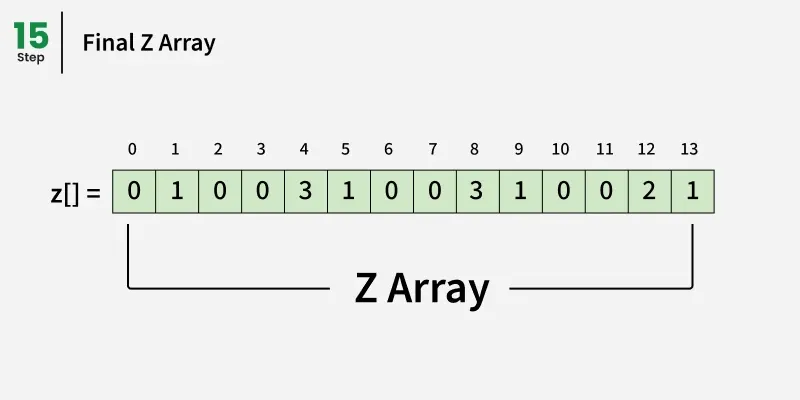
import java.util.ArrayList;
import java.util.Arrays;

public class GfG {
    
    // Z-function to compute Z-array
    static ArrayList<Integer> zFunction(String s) {
        int n = s.length();
        ArrayList<Integer> z = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            z.add(0);
        }
        int l = 0, r = 0;
        
        for (int i = 1; i < n; i++) {
            if (i <= r) {
                int k = i - l;
                
                // Case 2: reuse the previously computed value
                z.set(i, Math.min(r - i + 1, z.get(k)));
            }
            
            // Try to extend the Z-box beyond r
            while (i + z.get(i) < n && 
                    s.charAt(z.get(i)) == s.charAt(i + z.get(i))) {
                z.set(i, z.get(i) + 1);
            }
            
            // Update the [l, r] window if extended
            if (i + z.get(i) - 1 > r) {
                l = i;
                r = i + z.get(i) - 1;
            }
        }
        
        return z;
    }
    
    // Function to find all occurrences of pattern in text
    static ArrayList<Integer> search(String text, String pattern) {
        String s = pattern + '$' + text;
        ArrayList<Integer> z = zFunction(s);
        ArrayList<Integer> pos = new ArrayList<>();
        int m = pattern.length();
        
        for (int i = m + 1; i < z.size(); i++) {
            if (z.get(i) == m){
                
                // pattern match starts here in text
                pos.add(i - m - 1); 
            }
        }
        return pos;
    }

    public static void main(String[] args) {
        String text = "aabxaabxaa";
        String pattern = "aab";
        
        ArrayList<Integer> matches = search(text, pattern);
        
        for (int pos : matches)
            System.out.print(pos + " ");
    }
}

输出

0 4

时间复杂度：O（n + m），其中n是文本长度，m是图案长度，因为字符串和Z数组的组合是线性处理的。

辅助空间：O（n + m），用于存储组合字符串和Z数组，实现高效的模式匹配。

Z算法的优势

模式匹配的线性时间复杂度。

使用前缀比较，避免对匹配字符进行重新评估。

比KMP更容易编写;直接与前缀匹配工作。

对于多字符串问题的预处理非常有用，除了模式匹配之外。

现实应用

文本编辑器中的搜索工具（例如 VsCode、Sublime）

抄袭检测系统（检测重复阻挡）

生物信息学（寻找精确的DNA/RNA模式匹配）

入侵检测系统（匹配已知威胁特征）

编译器（识别重复序列或关键词）

信息检索（文档或关键词扫描）