再说质数，根据虚数单位的定义，
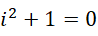
它是一个周期的描述，这个周期写做0，但实际上是任意数。假定虚数单位此处为正整数，那么0这个周期就可以是对应的正整数。因为虚数单位可取值为无限多，所以这个周期可取值也是无限多个。我们要求证明的是形如，
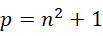
的质数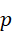 
有无限多个。尝试反证法，假定形如此方程的质数有有限多个，最后一个是，
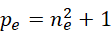
那么这个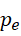 
就对应于一个 
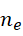。我们把这个 
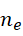当成以 
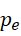为周期的虚数单位。
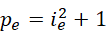
这就意味着，下一个或者之后的某一个质数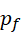 
，就永远不可能写成，
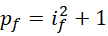
此时，
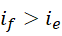
也就是不会再有任何虚数单位能够构成周期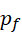 
。如果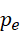 
不是最后一个可由此构成的质数，那么就总有下一个 
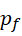，使得，
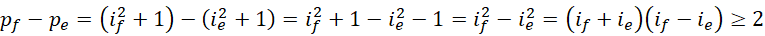
继续计算，
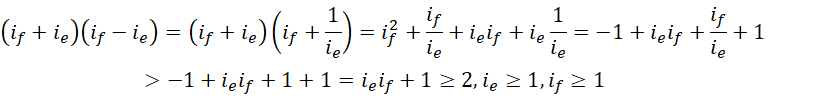
即，
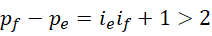
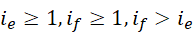
极限情况，
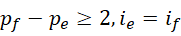
所以，若假定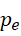 
为最后一个符合条件的质数，那么 
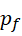就是它的孪生质数。这些运算实际上并不要求 
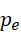和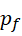 
为质数，但是却给出了周期之差至少为2的理由。考虑前几个周期的大小，
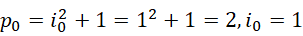
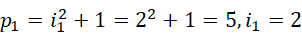
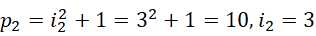
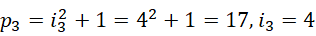
可见周期并不一定是质数。其中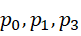 
是质数，而且相继两个周期的间隔都大于2。但若是从虚数单位为相继整数来考虑，则相继的周期之间的差，
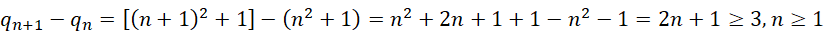
大于等于3。这体现出，虚数单位在这里起到了特殊的作用，
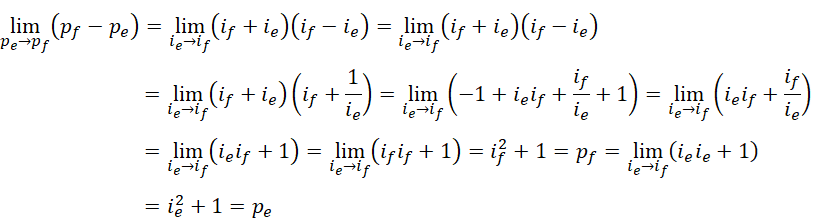
也就是说，
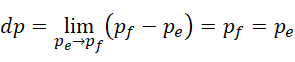
这显示出，当虚数单位极大且相互接近的时候，两个相邻周期的差，等于其中一个周期的大小，也就是说，
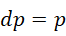
这相当于一种迭代形式，即从某个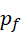 
开始，周期呈现以 
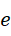为底的指数形式的增长，
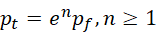
现在，有质数周期，
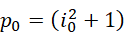
它的后面是否总是有质数，使得，
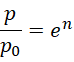
当然此处的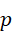 
不一定为质数。下面我们看 
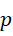必须为质数的情况。
回到黎曼泽塔函数，
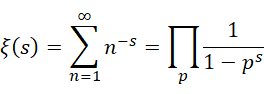
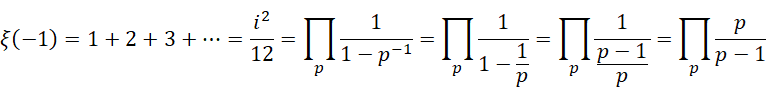
得到，
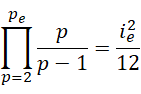
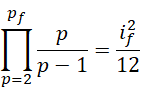
如果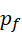 
是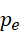 
的下一个质数，两者相比就剩下只含有 
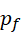的形式，
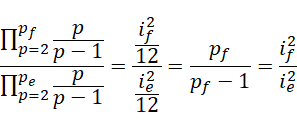
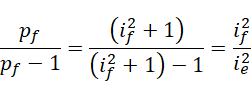
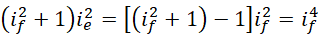
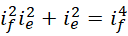
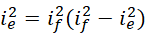
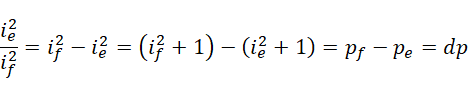
如果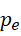 
是最后一个满足条件的质数，此时对应整数 
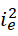存在，那么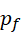 
作为下一个质数，就不能对应整数 
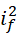存在，但是，
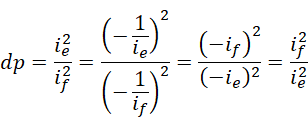
也就是说，对应条件对于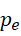 
和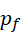 
可以互换，所以 
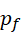存在的原因和 
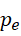存在的原因相同，即 
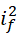必须为整数。此时虚数单位的平方为整数，并不能保证虚数单位本身为整数，但是这里的虚数单位以及它的平方表示的是数列的项数，所以它必须为整数。由此，若 
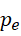是最后一个满足 
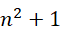形式的质数，则必有 
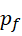为下一个满足 
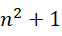形式的质数，也就是说，满足 
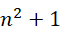形式的质数的个数是无限多的。
再看，如果写成这种形式，
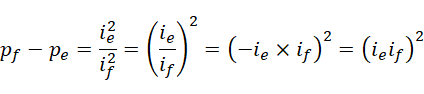
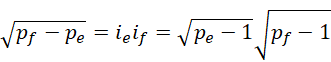
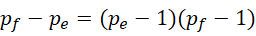
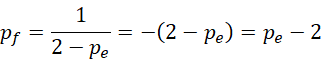
这表示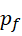 
和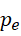 
为孪生素数，而 
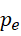有无限多个，也同时证明了孪生素数有无限多个。
其中，
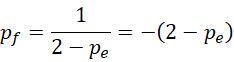
表示的是，周期也可以被认为是虚数单位，若是在它的平方加一之中，所以它可以等于它的负倒数，也就是，
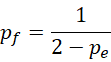
表示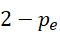 
同为周期，而，
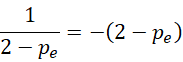
表示周期等于自身的负倒数。
最后，看看如何推导质数，根据质数之差和虚数单位的对应关系，
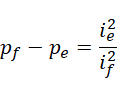
假定，
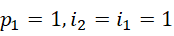
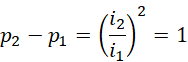
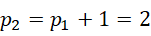
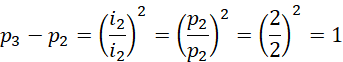
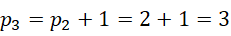
综合为，
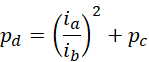
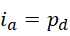
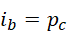
从，
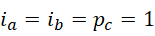
开始，迭代出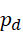 
，再代回重用，所有的数值都从这个过程导出，并保证 
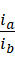总是能整除，然后对产生的结果排序。所以结果并不是序列而是一棵树，排序之后才是序列。
观察这个算法，这个算法显然不是线性的，每生成一个数，都会被重新代回到算法中，算法可以并行实现，而并行的过程中产生结果的数量必然是按照指数形式暴涨的。所以这些数值就和周期一样会排列在自然对数的增长曲线上，但是生成那个数的时机却不是按照自然数自增顺序来进行的。但是在任何一个子分支上先前生成的数量决定后来生成的数量出现的时机，暂时认为，也可能有多个分支产生相同的数量进而导致增长树之间的交叠。试图在自然数序列上预测下一个质数的想法是极其困难的，但是顺着一个特定的分支推演出下一个质数则是顺水推舟的事，而顺序产生全局最大的质数则极度是困难的，但如果生成的方式转换为特定分支的特定增长方向，则是极其容易的，只需要反复迭代即可。