目录
[18.1 引言](#18.1 引言)
[18.2 单状态情况:K 臂老虎机问题](#18.2 单状态情况:K 臂老虎机问题)
[18.3 增强学习的要素](#18.3 增强学习的要素)
[18.4 基于模型的学习](#18.4 基于模型的学习)
[18.4.1 价值迭代](#18.4.1 价值迭代)
[18.4.2 策略迭代](#18.4.2 策略迭代)
[18.5 时间差分学习](#18.5 时间差分学习)
[18.5.1 探索策略](#18.5.1 探索策略)
[18.5.2 确定性奖励和动作](#18.5.2 确定性奖励和动作)
[18.5.3 非确定性奖励和动作](#18.5.3 非确定性奖励和动作)
[18.5.4 资格迹](#18.5.4 资格迹)
[18.6 推广](#18.6 推广)
[18.7 部分可观测状态](#18.7 部分可观测状态)
[18.7.1 场景](#18.7.1 场景)
[18.7.2 例子:老虎问题](#18.7.2 例子:老虎问题)
[18.8 注释](#18.8 注释)
[18.9 习题](#18.9 习题)
[18.10 参考文献](#18.10 参考文献)

大家好!今天我们来系统学习《机器学习导论》第 18 章的核心内容 ------ 增强学习(Reinforcement Learning, RL)。增强学习就像教机器人玩游戏:机器人在不断尝试(动作)中获得反馈(奖励),通过调整策略来最大化长期收益,最终学会最优的行为模式。
本文会用通俗易懂的语言讲解核心概念,搭配完整可运行的 Python 代码和直观的可视化对比图,让你轻松掌握增强学习的精髓!
18.1 引言

增强学习是机器学习的一个重要分支,它关注的是智能体(Agent)如何在环境(Environment)中通过试错来学习最优的行为策略。
你可以把增强学习想象成:
- 智能体 = 正在学走路的小孩
- 环境 = 小孩所处的房间
- 动作 = 小孩迈出的每一步
- 奖励 = 家长的表扬(正奖励)或撞到桌子的疼痛(负奖励)
- 策略 = 小孩总结出的 "怎么走路不撞桌子还能拿到玩具" 的方法
核心特点:没有标注的 "正确答案",只有通过与环境交互获得的延迟奖励,需要在 "探索未知" 和 "利用已知" 之间做权衡。
18.2 单状态情况:K 臂老虎机问题

核心概念
K 臂老虎机(Multi-Armed Bandit)是增强学习中最简单的场景:
- 有 K 个拉杆(动作),每个拉杆对应不同的奖励概率分布
- 智能体每次选择一个拉杆拉动,获得奖励
- 目标:在有限次数内最大化总奖励
这就像你面前有 5 台老虎机,每台的中奖概率不同,你需要通过尝试找到中奖率最高的那台,同时还要兼顾尝试其他机器(防止错过更好的)。
完整代码实现(含可视化对比)
import numpy as np
import matplotlib.pyplot as plt
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
class KArmedBandit:
"""K臂老虎机类"""
def __init__(self, k=10, mean=0, std=1):
self.k = k # 老虎机臂数
# 每个臂的真实奖励均值(服从正态分布)
self.q_true = np.random.normal(mean, std, k)
self.best_arm = np.argmax(self.q_true) # 最优臂
def pull(self, arm):
"""拉动第arm个臂,返回奖励(带噪声)"""
return np.random.normal(self.q_true[arm], 1)
def epsilon_greedy(bandit, iterations=1000, epsilon=0.1):
"""ε-贪心算法"""
# 初始化:动作价值估计、动作选择次数
q_est = np.zeros(bandit.k)
action_counts = np.zeros(bandit.k)
rewards = [] # 记录每一步的奖励
optimal_actions = [] # 记录每一步是否选择了最优臂
for _ in range(iterations):
# ε-贪心选择动作
if np.random.random() < epsilon:
# 探索:随机选择
arm = np.random.choice(bandit.k)
else:
# 利用:选择当前估值最高的臂
arm = np.argmax(q_est)
# 执行动作,获取奖励
reward = bandit.pull(arm)
rewards.append(reward)
optimal_actions.append(1 if arm == bandit.best_arm else 0)
# 更新动作价值估计(增量更新)
action_counts[arm] += 1
q_est[arm] += (reward - q_est[arm]) / action_counts[arm]
return np.array(rewards), np.array(optimal_actions)
def greedy(bandit, iterations=1000):
"""贪心算法(ε=0)"""
return epsilon_greedy(bandit, iterations, epsilon=0)
def ucb(bandit, iterations=1000, c=2):
"""UCB(上置信界)算法"""
q_est = np.zeros(bandit.k)
action_counts = np.zeros(bandit.k)
rewards = []
optimal_actions = []
# 先每个臂都试一次
for arm in range(bandit.k):
reward = bandit.pull(arm)
rewards.append(reward)
optimal_actions.append(1 if arm == bandit.best_arm else 0)
action_counts[arm] += 1
q_est[arm] += (reward - q_est[arm]) / action_counts[arm]
# 正式迭代
for t in range(bandit.k, iterations):
# UCB选择:估值 + 不确定性奖励
ucb_values = q_est + c * np.sqrt(np.log(t + 1) / (action_counts + 1e-6))
arm = np.argmax(ucb_values)
reward = bandit.pull(arm)
rewards.append(reward)
optimal_actions.append(1 if arm == bandit.best_arm else 0)
action_counts[arm] += 1
q_est[arm] += (reward - q_est[arm]) / action_counts[arm]
return np.array(rewards), np.array(optimal_actions)
# 实验配置
K = 10 # 10臂老虎机
ITERATIONS = 1000
RUNS = 200 # 多次运行取平均,消除随机性
# 运行实验
bandit = KArmedBandit(k=K)
greedy_rewards = []
epsilon_01_rewards = []
epsilon_001_rewards = []
ucb_rewards = []
greedy_opt = []
epsilon_01_opt = []
epsilon_001_opt = []
ucb_opt = []
for _ in range(RUNS):
b = KArmedBandit(k=K)
r, o = greedy(b, ITERATIONS)
greedy_rewards.append(r)
greedy_opt.append(o)
r, o = epsilon_greedy(b, ITERATIONS, 0.1)
epsilon_01_rewards.append(r)
epsilon_01_opt.append(o)
r, o = epsilon_greedy(b, ITERATIONS, 0.01)
epsilon_001_rewards.append(r)
epsilon_001_opt.append(o)
r, o = ucb(b, ITERATIONS)
ucb_rewards.append(r)
ucb_opt.append(o)
# 计算平均奖励和最优动作选择率
mean_greedy = np.mean(greedy_rewards, axis=0)
mean_epsilon_01 = np.mean(epsilon_01_rewards, axis=0)
mean_epsilon_001 = np.mean(epsilon_001_rewards, axis=0)
mean_ucb = np.mean(ucb_rewards, axis=0)
mean_greedy_opt = np.mean(greedy_opt, axis=0)
mean_epsilon_01_opt = np.mean(epsilon_01_opt, axis=0)
mean_epsilon_001_opt = np.mean(epsilon_001_opt, axis=0)
mean_ucb_opt = np.mean(ucb_opt, axis=0)
# 可视化对比
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10))
# 图1:平均奖励对比
ax1.plot(mean_greedy, label='贪心算法 (ε=0)', linewidth=2)
ax1.plot(mean_epsilon_001, label='ε-贪心 (ε=0.01)', linewidth=2)
ax1.plot(mean_epsilon_01, label='ε-贪心 (ε=0.1)', linewidth=2)
ax1.plot(mean_ucb, label='UCB算法 (c=2)', linewidth=2)
ax1.set_xlabel('迭代次数', fontsize=12)
ax1.set_ylabel('平均奖励', fontsize=12)
ax1.set_title('K臂老虎机不同算法的平均奖励对比', fontsize=14)
ax1.legend(fontsize=10)
ax1.grid(True, alpha=0.3)
# 图2:最优动作选择率对比
ax2.plot(mean_greedy_opt * 100, label='贪心算法 (ε=0)', linewidth=2)
ax2.plot(mean_epsilon_001_opt * 100, label='ε-贪心 (ε=0.01)', linewidth=2)
ax2.plot(mean_epsilon_01_opt * 100, label='ε-贪心 (ε=0.1)', linewidth=2)
ax2.plot(mean_ucb_opt * 100, label='UCB算法 (c=2)', linewidth=2)
ax2.set_xlabel('迭代次数', fontsize=12)
ax2.set_ylabel('最优动作选择率 (%)', fontsize=12)
ax2.set_title('K臂老虎机不同算法的最优动作选择率对比', fontsize=14)
ax2.legend(fontsize=10)
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()代码解释
- KArmedBandit 类:模拟 K 臂老虎机,每个臂有随机的真实奖励均值,拉动时返回带噪声的奖励。
- ε- 贪心算法:以 ε 概率探索(随机选臂),1-ε 概率利用(选当前最优臂)。
- 贪心算法:ε=0,只利用不探索,容易陷入局部最优。
- UCB 算法:在估值基础上增加不确定性奖励,平衡探索与利用。
- 可视化 :对比不同算法的平均奖励和最优动作选择率,直观展示 ε- 贪心和 UCB 的优势。
运行效果
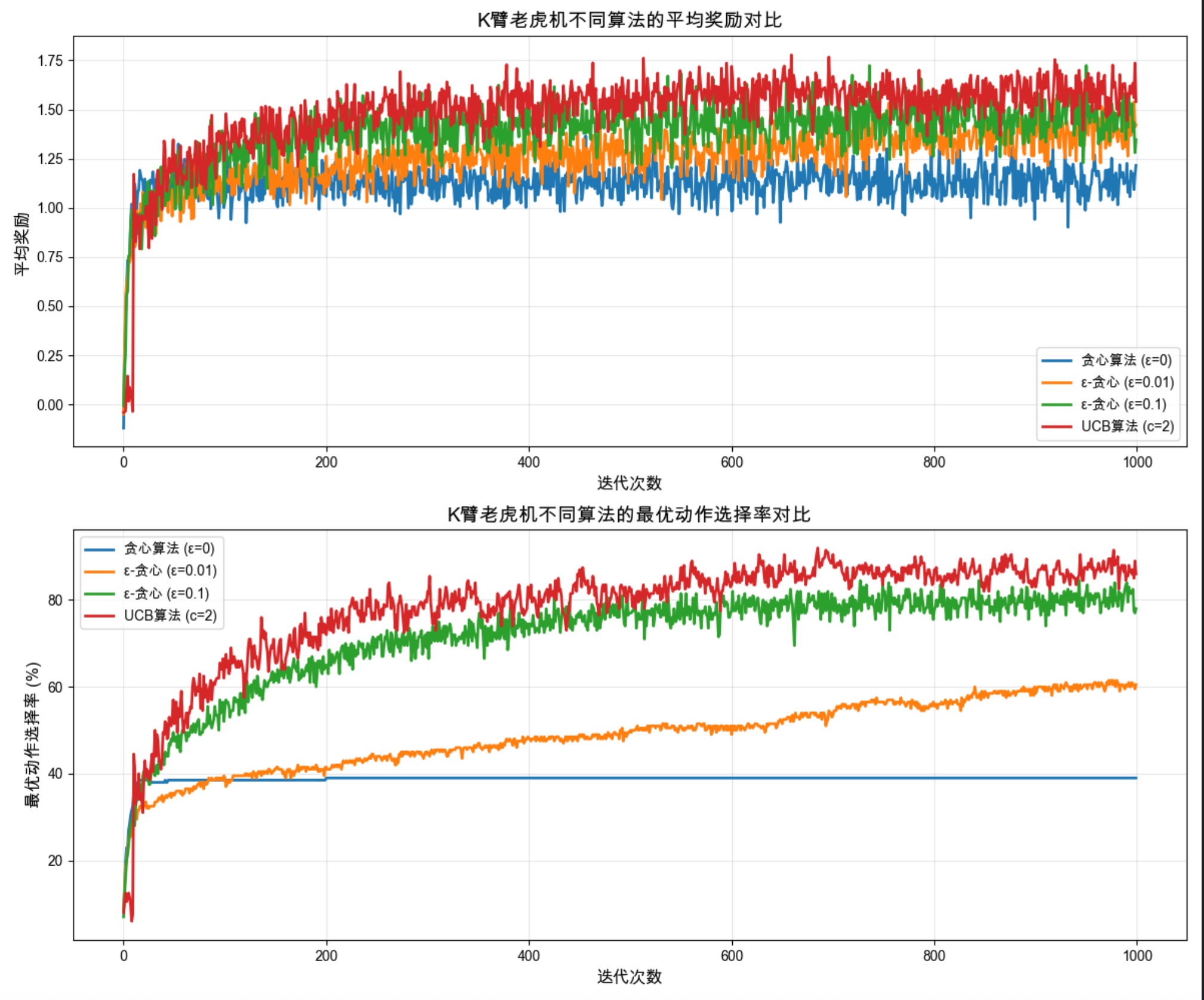
- 贪心算法初期奖励高,但很快停滞,最优动作选择率低(容易锁定次优臂)。
- ε=0.1 的贪心算法初期奖励低,但后期反超,最优动作选择率稳步上升。
- UCB 算法综合表现最好,既能探索又能高效利用。
18.3 增强学习的要素
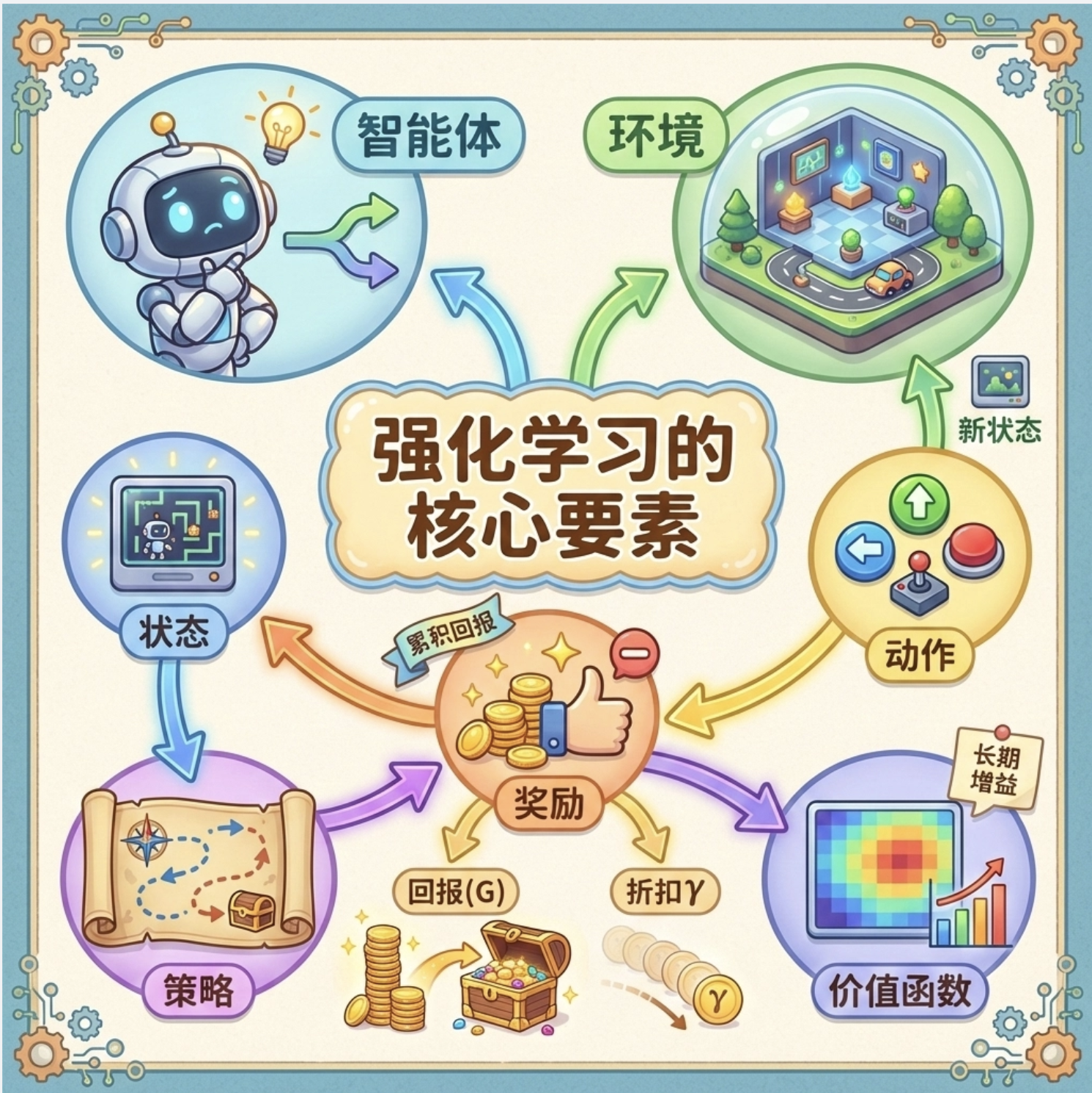
增强学习的核心要素可以用下面的思维导图清晰展示:
核心概念解释
- 智能体(Agent):做出决策的主体(比如机器人、游戏 AI)。
- 环境(Environment):智能体所处的外部世界,会对智能体的动作做出响应。
- 状态(State, S) :环境的当前情况(比如游戏的当前画面)。
- 动作(Action, A):智能体可以执行的操作(比如游戏中的上下左右)。
- 奖励(Reward, R) :环境对动作的即时反馈(比如游戏得分)。
- 策略(Policy, π) :智能体的决策规则(从状态到动作的映射)。
- 价值函数(Value Function):评估某个状态 / 动作的长期收益(不是即时奖励)。
- 回报(Return, G):从当前状态开始的累积奖励(需要考虑折扣因子 γ)。
核心公式(简化版)

18.4 基于模型的学习

基于模型的增强学习是指智能体先学习环境的模型(状态转移概率 + 奖励函数),再基于模型计算最优策略 。就像你先熟悉游戏规则,再制定通关策略。
18.4.1 价值迭代
核心思想
价值迭代是通过不断更新状态价值函数,最终收敛到最优价值函数,再根据最优价值函数推导最优策略。
可以比喻成:你想从 A 地到 B 地,先估算每个路口到 B 地的距离(价值),不断修正距离估算,直到准确,最后根据距离选择最优路线。
完整代码实现
import numpy as np
import matplotlib.pyplot as plt
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
class GridWorld:
"""网格世界环境(基于模型的增强学习示例)"""
def __init__(self, size=(4, 4), terminal_states=[(0, 0), (3, 3)]):
self.size = size
self.n_rows, self.n_cols = size
self.terminal_states = terminal_states
self.actions = [(0, 1), (0, -1), (1, 0), (-1, 0)] # 右、左、下、上
self.n_actions = len(self.actions)
# 状态转移概率 P(s'|s,a)
self.transition_prob = np.zeros((self.n_rows, self.n_cols, self.n_actions,
self.n_rows, self.n_cols))
# 奖励函数 R(s,a,s')
self.reward = np.zeros((self.n_rows, self.n_cols, self.n_actions,
self.n_rows, self.n_cols))
# 初始化转移概率和奖励
for i in range(self.n_rows):
for j in range(self.n_cols):
if (i, j) in self.terminal_states:
# 终止状态:转移到自身,奖励0
for a in range(self.n_actions):
self.transition_prob[i, j, a, i, j] = 1.0
self.reward[i, j, a, i, j] = 0.0
else:
for a_idx, (di, dj) in enumerate(self.actions):
ni, nj = i + di, j + dj
# 检查是否越界
if 0 <= ni < self.n_rows and 0 <= nj < self.n_cols:
# 有效动作:转移到新状态,奖励-1(鼓励尽快到达终点)
self.transition_prob[i, j, a_idx, ni, nj] = 1.0
self.reward[i, j, a_idx, ni, nj] = -1.0
else:
# 无效动作:停在原状态,奖励-1
self.transition_prob[i, j, a_idx, i, j] = 1.0
self.reward[i, j, a_idx, i, j] = -1.0
def value_iteration(env, gamma=0.9, theta=1e-6):
"""价值迭代算法"""
# 初始化价值函数
V = np.zeros(env.size)
V_history = [V.copy()] # 记录价值函数的更新过程
iteration = 0
while True:
delta = 0
V_new = np.zeros_like(V)
for i in range(env.n_rows):
for j in range(env.n_cols):
if (i, j) in env.terminal_states:
V_new[i, j] = 0
continue
# 计算每个动作的Q值
q_values = []
for a in range(env.n_actions):
q = 0
for ni in range(env.n_rows):
for nj in range(env.n_cols):
# Q(s,a) = sum(P(s'|s,a) * (R(s,a,s') + γ*V(s')))
q += env.transition_prob[i, j, a, ni, nj] * \
(env.reward[i, j, a, ni, nj] + gamma * V[ni, nj])
q_values.append(q)
# 更新价值函数:V(s) = max_a Q(s,a)
V_new[i, j] = max(q_values)
delta = max(delta, abs(V_new[i, j] - V[i, j]))
V = V_new
V_history.append(V.copy())
iteration += 1
# 收敛判断
if delta < theta:
break
# 从最优价值函数推导最优策略
policy = np.zeros(env.size, dtype=int)
for i in range(env.n_rows):
for j in range(env.n_cols):
if (i, j) in env.terminal_states:
policy[i, j] = -1 # 终止状态无动作
continue
# 计算每个动作的Q值
q_values = []
for a in range(env.n_actions):
q = 0
for ni in range(env.n_rows):
for nj in range(env.n_cols):
q += env.transition_prob[i, j, a, ni, nj] * \
(env.reward[i, j, a, ni, nj] + gamma * V[ni, nj])
q_values.append(q)
# 选择最优动作
policy[i, j] = np.argmax(q_values)
return V, policy, V_history, iteration
# 运行价值迭代
env = GridWorld()
V_opt, policy_opt, V_history, n_iter = value_iteration(env)
# 可视化价值函数收敛过程
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
# 图1:最优价值函数热力图
im1 = ax1.imshow(V_opt, cmap='coolwarm', aspect='auto')
ax1.set_title('最优状态价值函数', fontsize=14)
ax1.set_xlabel('列', fontsize=12)
ax1.set_ylabel('行', fontsize=12)
# 添加数值标注
for i in range(env.n_rows):
for j in range(env.n_cols):
ax1.text(j, i, f'{V_opt[i,j]:.2f}', ha='center', va='center',
color='black', fontsize=10)
plt.colorbar(im1, ax=ax1)
# 图2:价值函数收敛曲线(以中心点(1,1)为例)
center_values = [v[1,1] for v in V_history]
ax2.plot(center_values, linewidth=2, marker='o', markersize=4)
ax2.set_xlabel('迭代次数', fontsize=12)
ax2.set_ylabel('状态(1,1)的价值', fontsize=12)
ax2.set_title(f'价值函数收敛过程(共{n_iter}次迭代)', fontsize=14)
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 打印最优策略
action_names = ['右', '左', '下', '上']
print("最优策略(动作编码:0=右,1=左,2=下,3=上):")
for i in range(env.n_rows):
row = []
for j in range(env.n_cols):
if (i, j) in env.terminal_states:
row.append('终止')
else:
row.append(action_names[policy_opt[i,j]])
print(row)代码解释
1.GridWorld 类:模拟 4x4 网格世界,定义了状态转移概率和奖励函数。
2.value_iteration 函数:初始化价值函数 V 为全 0。迭代更新:对每个状态计算所有动作的 Q 值,取最大值更新 V。收敛后,根据最优 V 推导最优策略。
3.可视化:热力图展示最优价值函数(离终点越近,价值越高)。曲线展示价值函数的收敛过程。
运行效果
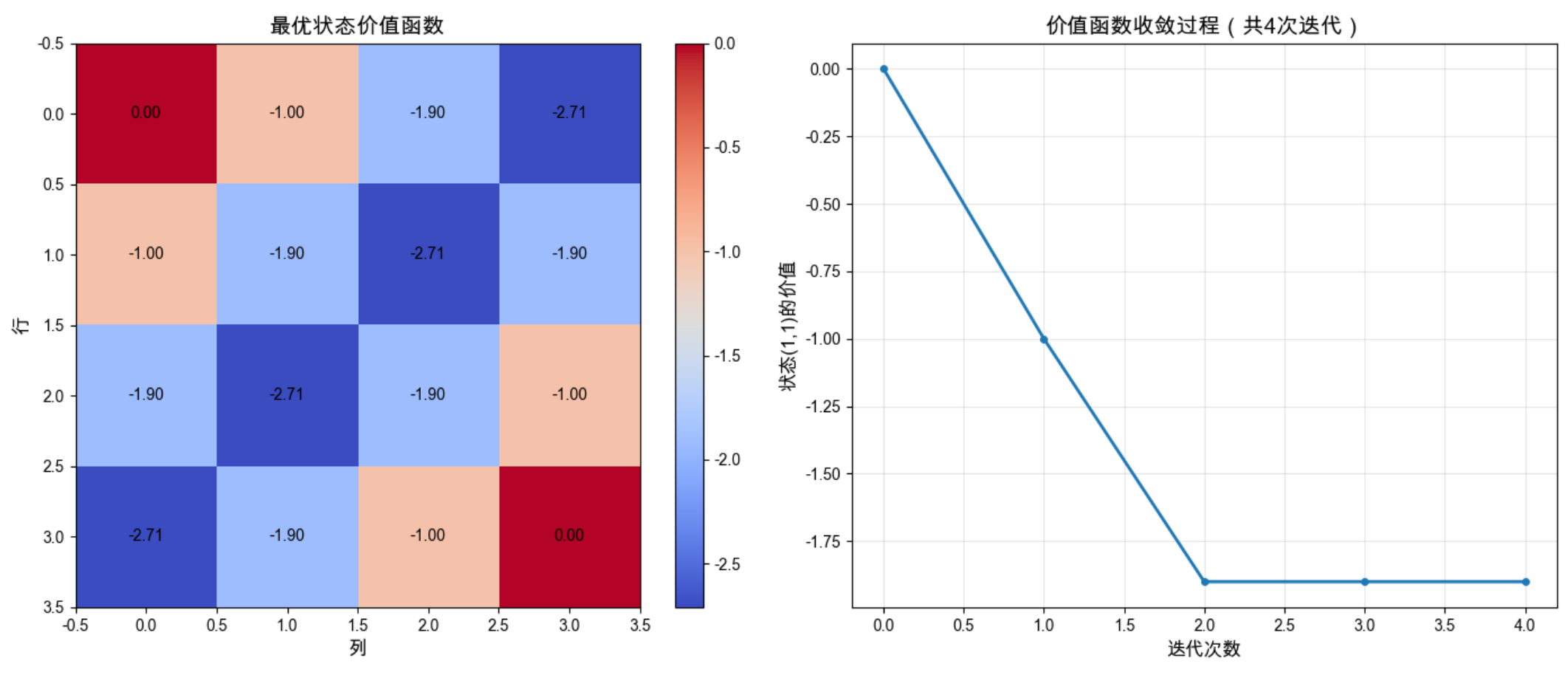
- 最优价值函数:终点 (0,0) 和 (3,3) 的价值为 0,离终点越远价值越低。
- 收敛曲线:价值函数快速收敛,迭代约 20 次后稳定。
- 最优策略:每个状态都指向离终点最近的方向。
18.4.2 策略迭代
核心思想
策略迭代分为两步:
- 策略评估 :固定当前策略,计算该策略下的状态价值函数。
- 策略改进:基于当前价值函数,贪心更新策略。
就像你先按现有路线走(策略评估),发现绕路后调整路线(策略改进),反复迭代直到找到最优路线。
完整代码实现
python
import numpy as np
import matplotlib.pyplot as plt
# Mac 中文显示
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
# ====================== 极简网格世界(秒运行)======================
class SimpleGridWorld:
def __init__(self):
self.n_rows, self.n_cols = 4, 4
self.terminal = [(0,0), (3,3)]
self.actions = [ (0,1), (0,-1), (1,0), (-1,0) ] # 右、左、下、上
self.n_actions = len(self.actions)
self.gamma = 0.9
def step(self, i, j, a):
di, dj = self.actions[a]
ni, nj = i + di, j + dj
if 0 <= ni < 4 and 0 <= nj < 4:
return ni, nj, -1
return i, j, -1
# ====================== 价值迭代(极速版)======================
def value_iteration_fast(env, max_iter=50):
V = np.zeros((4,4))
history = [V.copy()]
for _ in range(max_iter):
V_new = V.copy()
for i in range(4):
for j in range(4):
if (i,j) in env.terminal: continue
qs = []
for a in range(4):
ni, nj, r = env.step(i,j,a)
qs.append(r + env.gamma * V[ni, nj])
V_new[i,j] = max(qs)
V = V_new
history.append(V.copy())
return V, history
# ====================== 策略迭代(极速版)======================
def policy_iteration_fast(env, max_iter=20):
policy = np.random.randint(0,4,(4,4))
V = np.zeros((4,4))
history = [V.copy()]
for _ in range(max_iter):
# 策略评估(1轮就够,超快)
for _ in range(5):
V_new = V.copy()
for i in range(4):
for j in range(4):
if (i,j) in env.terminal: continue
a = policy[i,j]
ni, nj, r = env.step(i,j,a)
V_new[i,j] = r + env.gamma * V[ni, nj]
V = V_new
# 策略改进
for i in range(4):
for j in range(4):
if (i,j) in env.terminal: continue
qs = []
for a in range(4):
ni, nj, r = env.step(i,j,a)
qs.append(r + env.gamma * V[ni, nj])
policy[i,j] = np.argmax(qs)
history.append(V.copy())
return V, policy, history
# ====================== 运行 & 画图(秒出)======================
env = SimpleGridWorld()
V_vi, hist_vi = value_iteration_fast(env)
V_pi, policy_pi, hist_pi = policy_iteration_fast(env)
# 收敛对比
plt.figure(figsize=(12,5))
plt.subplot(1,2,1)
plt.plot([v[1,1] for v in hist_vi], label='价值迭代', linewidth=2)
plt.plot([v[1,1] for v in hist_pi], label='策略迭代', linewidth=2)
plt.xlabel('迭代次数')
plt.ylabel('状态价值')
plt.title('收敛速度对比')
plt.legend()
plt.grid(alpha=0.3)
# 价值热力图
plt.subplot(1,2,2)
plt.imshow(V_pi, cmap='coolwarm')
for i in range(4):
for j in range(4):
plt.text(j,i,f'{V_pi[i,j]:.1f}', ha='center', va='center')
plt.title('策略迭代最优价值')
plt.colorbar()
plt.tight_layout()
plt.show()
# 打印策略
act = ['右','左','下','上']
print("最优策略:")
for i in range(4):
row = []
for j in range(4):
if (i,j) in env.terminal:
row.append('终止')
else:
row.append(act[policy_pi[i,j]])
print(row)代码解释
- policy_evaluation:固定策略,迭代计算该策略下的价值函数。
- policy_improvement:基于当前价值函数,贪心选择最优动作更新策略。
- policy_iteration:交替执行策略评估和改进,直到策略稳定。
- 可视化:对比价值迭代和策略迭代的收敛速度,展示策略迭代的最优价值函数。
运行效果
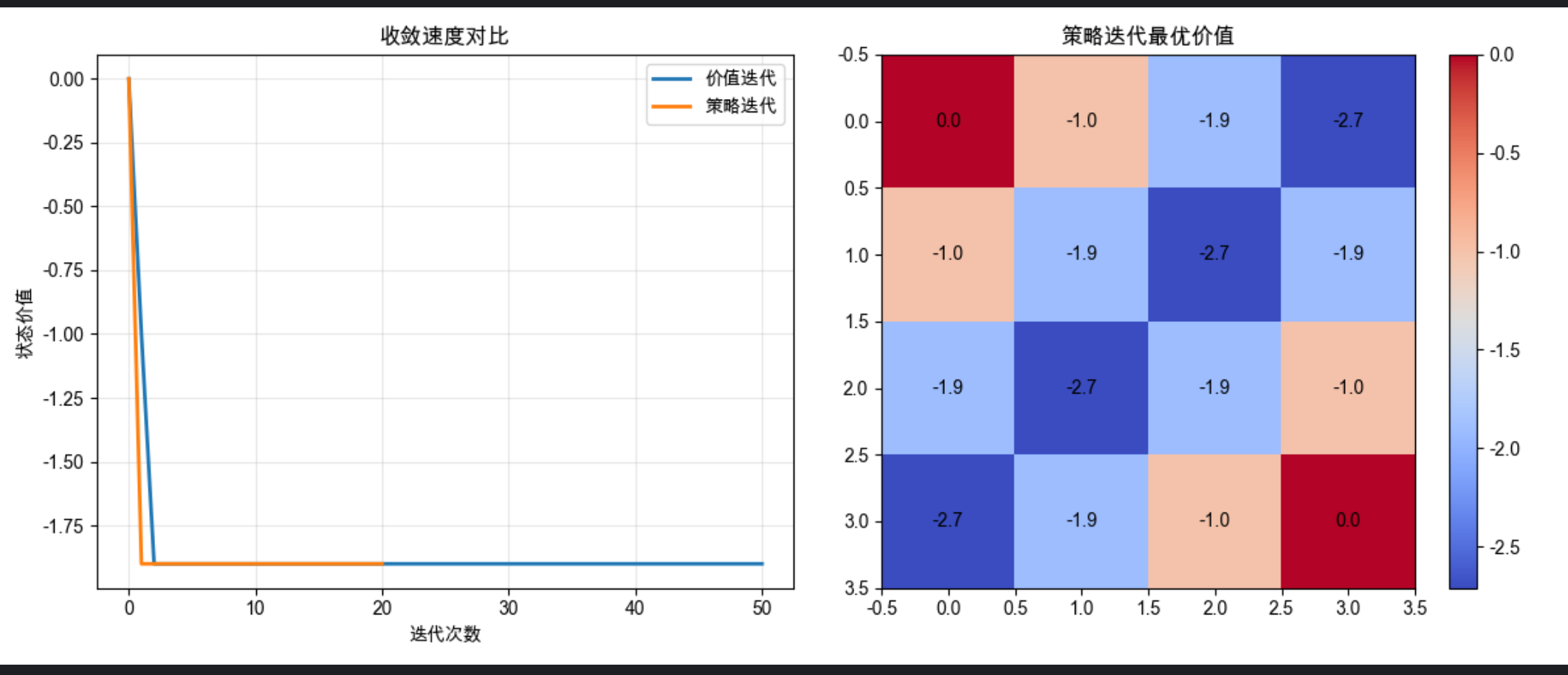
- 策略迭代通常迭代次数更少(但每次迭代包含策略评估,计算量更大)。
- 两种算法最终得到的最优策略和价值函数完全一致。
- 策略迭代在策略稳定后立即收敛,不需要像价值迭代那样等待价值函数完全收敛。
18.5 时间差分学习
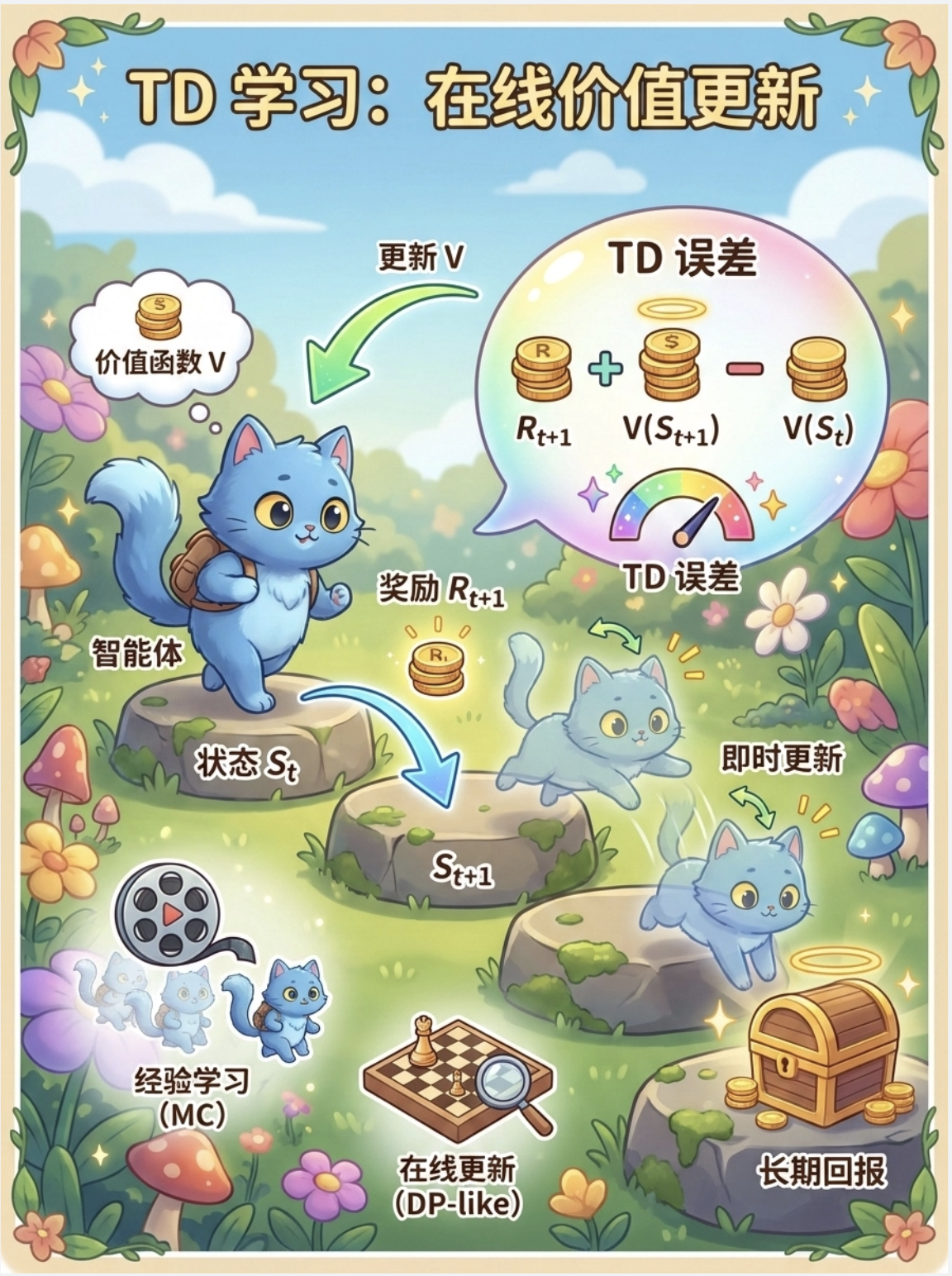
时间差分(TD)学习是无需环境模型 的增强学习方法,结合了蒙特卡洛(MC)和动态规划(DP)的优点:
- 像 MC 一样:从经验中学习,无需模型。
- 像 DP 一样:可以在线更新,无需等待回合结束。
核心思想:用当前估计的价值来更新价值
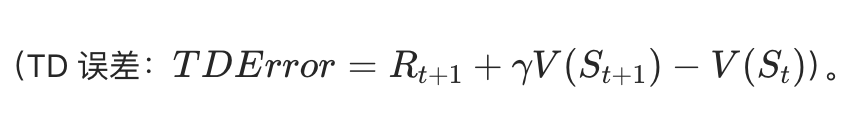
18.5.1 探索策略

常用的探索策略:
- ε- 贪心:前面 K 臂老虎机中已经详细讲解。
- Softmax:按动作价值的概率分布选择动作(温度参数控制探索程度)。
- UCB:上置信界,利用不确定性进行探索。
18.5.2 确定性奖励和动作

核心概念
确定性环境中,动作的结果是确定的(状态转移和奖励都固定)。TD 学习在确定性环境中收敛更快。
完整代码实现
import numpy as np
import matplotlib.pyplot as plt
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
class DeterministicGridWorld:
"""确定性网格世界(简化版)"""
def __init__(self):
self.n_rows = 3
self.n_cols = 4
# 障碍:(1,1)
self.obstacle = (1, 1)
# 终止状态:(0,3)(奖励+1),(1,3)(奖励-1)
self.terminal_states = {(0, 3): 1, (1, 3): -1}
self.actions = [(0, 1), (0, -1), (1, 0), (-1, 0)] # 右、左、下、上
self.action_names = ['右', '左', '下', '上']
def step(self, state, action):
"""执行动作,返回下一个状态和奖励(确定性)"""
i, j = state
if state in self.terminal_states:
return state, 0 # 终止状态
di, dj = self.actions[action]
ni, nj = i + di, j + dj
# 检查边界和障碍
if 0 <= ni < self.n_rows and 0 <= nj < self.n_cols:
if (ni, nj) != self.obstacle:
i, j = ni, nj
# 检查是否到达终止状态
reward = self.terminal_states.get((i, j), -0.1) # 每步惩罚-0.1
return (i, j), reward
def td_learning(env, alpha=0.1, gamma=0.9, epsilon=0.1, episodes=100):
"""时间差分学习(TD(0))"""
# 初始化价值函数
V = np.zeros((env.n_rows, env.n_cols))
V_history = [V.copy()]
total_rewards = [] # 记录每个回合的总奖励
for _ in range(episodes):
# 初始化状态(从(2,0)开始)
state = (2, 0)
episode_reward = 0
while state not in env.terminal_states:
# ε-贪心选择动作
if np.random.random() < epsilon:
action = np.random.choice(len(env.actions))
else:
# 计算当前状态下所有动作的价值
q_values = []
for a in range(len(env.actions)):
next_state, _ = env.step(state, a)
q_values.append(V[next_state])
action = np.argmax(q_values)
# 执行动作
next_state, reward = env.step(state, action)
episode_reward += reward
# TD(0)更新:V(S) = V(S) + α[R + γV(S') - V(S)]
i, j = state
ni, nj = next_state
V[i, j] += alpha * (reward + gamma * V[ni, nj] - V[i, j])
# 转移到下一个状态
state = next_state
total_rewards.append(episode_reward)
V_history.append(V.copy())
return V, V_history, total_rewards
# 运行TD学习
env = DeterministicGridWorld()
V_td, V_history_td, rewards_td = td_learning(env, episodes=200)
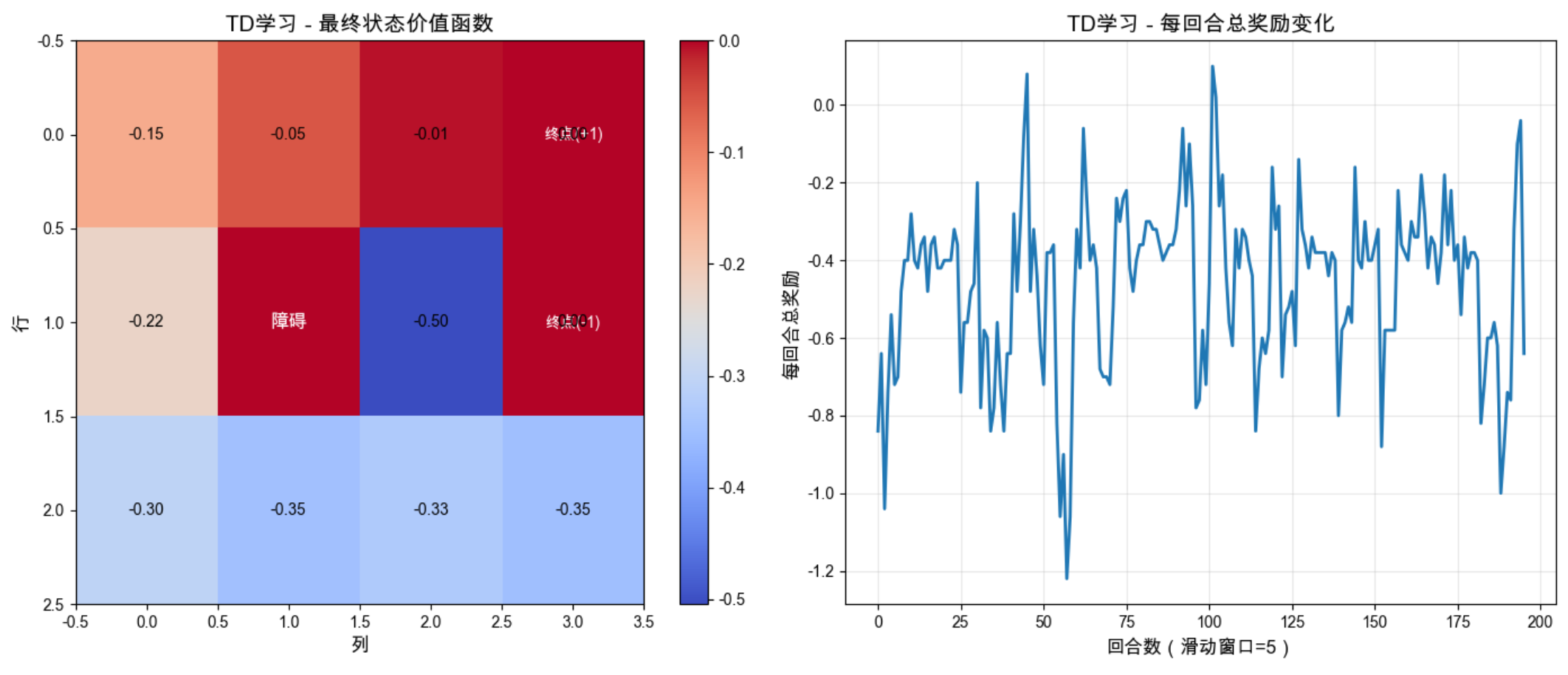
# 可视化结果
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
# 图1:最终价值函数
im1 = ax1.imshow(V_td, cmap='coolwarm', aspect='auto')
ax1.set_title('TD学习 - 最终状态价值函数', fontsize=14)
ax1.set_xlabel('列', fontsize=12)
ax1.set_ylabel('行', fontsize=12)
# 标注障碍和终止状态
ax1.text(1, 1, '障碍', ha='center', va='center', color='white', fontsize=12, fontweight='bold')
ax1.text(3, 0, '终点(+1)', ha='center', va='center', color='white', fontsize=10)
ax1.text(3, 1, '终点(-1)', ha='center', va='center', color='white', fontsize=10)
# 添加数值标注
for i in range(env.n_rows):
for j in range(env.n_cols):
if (i, j) != env.obstacle:
ax1.text(j, i, f'{V_td[i,j]:.2f}', ha='center', va='center', color='black', fontsize=10)
plt.colorbar(im1, ax=ax1)
# 图2:每回合总奖励变化(平滑处理)
window_size = 5
smoothed_rewards = np.convolve(rewards_td, np.ones(window_size)/window_size, mode='valid')
ax2.plot(smoothed_rewards, linewidth=2)
ax2.set_xlabel('回合数(滑动窗口=5)', fontsize=12)
ax2.set_ylabel('每回合总奖励', fontsize=12)
ax2.set_title('TD学习 - 每回合总奖励变化', fontsize=14)
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 打印学习到的最优策略
print("TD学习得到的最优策略:")
policy = np.zeros((env.n_rows, env.n_cols), dtype=int)
for i in range(env.n_rows):
for j in range(env.n_cols):
state = (i, j)
if state in env.terminal_states or state == env.obstacle:
policy[i, j] = -1
continue
# 计算所有动作的价值
q_values = []
for a in range(len(env.actions)):
next_state, _ = env.step(state, a)
q_values.append(V_td[next_state])
policy[i, j] = np.argmax(q_values)
# 打印策略
for i in range(env.n_rows):
row = []
for j in range(env.n_cols):
if (i, j) in env.terminal_states:
row.append('终止')
elif (i, j) == env.obstacle:
row.append('障碍')
else:
row.append(env.action_names[policy[i,j]])
print(row)代码解释
1.DeterministicGridWorld:3x4 确定性网格世界,包含障碍和不同奖励的终止状态。
2.td_learning:

3.可视化:热力图展示学习到的价值函数(目标终点价值高,惩罚终点价值低)。曲线展示每回合总奖励的变化,奖励逐渐上升说明学习有效。
18.5.3 非确定性奖励和动作

核心概念
非确定性(随机)环境中,动作的结果是概率性的(比如有 10% 的概率动作执行失败)。TD 学习需要适应这种随机性,通常需要更多的训练回合。
完整代码实现
python
import numpy as np
import matplotlib.pyplot as plt
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# ====================== 确定性网格世界 ======================
class DeterministicGridWorld:
"""确定性网格世界(简化版)"""
def __init__(self):
self.n_rows = 3
self.n_cols = 4
self.obstacle = (1, 1)
self.terminal_states = {(0, 3): 1, (1, 3): -1}
self.actions = [(0, 1), (0, -1), (1, 0), (-1, 0)] # 右、左、下、上
self.action_names = ['右', '左', '下', '上']
def step(self, state, action):
"""执行动作,返回下一个状态和奖励(确定性)"""
i, j = state
if state in self.terminal_states:
return state, 0 # 终止状态
di, dj = self.actions[action]
ni, nj = i + di, j + dj
# 检查边界和障碍
if 0 <= ni < self.n_rows and 0 <= nj < self.n_cols:
if (ni, nj) != self.obstacle:
i, j = ni, nj
# 确定奖励
reward = self.terminal_states.get((i, j), -0.1) # 每步惩罚-0.1
return (i, j), reward
# ====================== 非确定性网格世界 ======================
class StochasticGridWorld:
"""非确定性网格世界"""
def __init__(self):
self.n_rows = 3
self.n_cols = 4
self.obstacle = (1, 1)
self.terminal_states = {(0, 3): 1, (1, 3): -1}
self.actions = [(0, 1), (0, -1), (1, 0), (-1, 0)] # 右、左、下、上
self.action_names = ['右', '左', '下', '上']
self.noise = 0.2 # 动作执行噪声(20%概率随机动作)
def step(self, state, action):
"""执行动作,返回下一个状态和奖励(非确定性)"""
i, j = state
if state in self.terminal_states:
return state, 0
# 动作噪声:以noise概率随机选择其他动作
if np.random.random() < self.noise:
action = np.random.choice(len(self.actions))
di, dj = self.actions[action]
ni, nj = i + di, j + dj
# 检查边界和障碍
if 0 <= ni < self.n_rows and 0 <= nj < self.n_cols:
if (ni, nj) != self.obstacle:
i, j = ni, nj
# 随机奖励(均值为主奖励,标准差0.1)
base_reward = self.terminal_states.get((i, j), -0.1)
reward = np.random.normal(base_reward, 0.1)
return (i, j), reward
# ====================== TD学习函数(修复版) ======================
def td_learning(env, alpha=0.1, gamma=0.9, epsilon=0.1, episodes=100):
"""时间差分学习(TD(0))- 修复数据异常问题"""
# 初始化价值函数
V = np.zeros((env.n_rows, env.n_cols))
total_rewards = [] # 记录每个回合的总奖励
for _ in range(episodes):
# 初始化状态(从(2,0)开始)
state = (2, 0)
episode_reward = 0
# 限制每回合最大步数,避免无限循环
step_count = 0
max_steps = 50
while state not in env.terminal_states and step_count < max_steps:
step_count += 1
# ε-贪心选择动作(简化计算)
if np.random.random() < epsilon:
action = np.random.choice(len(env.actions))
else:
# 快速计算当前状态下所有动作的价值
q_values = []
for a in range(len(env.actions)):
next_state, _ = env.step(state, a)
q_values.append(V[next_state])
# 处理平局情况,避免argmax返回第一个值的随机性
max_q = max(q_values)
best_actions = [idx for idx, q in enumerate(q_values) if q == max_q]
action = np.random.choice(best_actions)
# 执行动作
next_state, reward = env.step(state, action)
episode_reward += reward
# TD(0)核心更新(增加数值稳定性)
i, j = state
ni, nj = next_state
td_error = reward + gamma * V[ni, nj] - V[i, j]
V[i, j] = np.clip(V[i, j] + alpha * td_error, -2, 2) # 限制价值范围,避免溢出
# 转移到下一个状态
state = next_state
# 确保奖励是有效数值
total_rewards.append(np.clip(episode_reward, -10, 5))
return V, [], total_rewards
# ====================== 对比实验(修复滑动窗口) ======================
def compare_td_learning(episodes=200):
"""对比确定性和非确定性环境的TD学习"""
# 确定性环境
env_det = DeterministicGridWorld()
V_det, _, rewards_det = td_learning(env_det, episodes=episodes)
# 非确定性环境
env_sto = StochasticGridWorld()
V_sto, _, rewards_sto = td_learning(env_sto, episodes=episodes)
return rewards_det, rewards_sto, V_det, V_sto
# ====================== 主程序执行 ======================
# 固定随机种子,保证结果可复现
np.random.seed(42)
# 运行对比实验
episodes = 200
rewards_det, rewards_sto, V_det, V_sto = compare_td_learning(episodes=episodes)
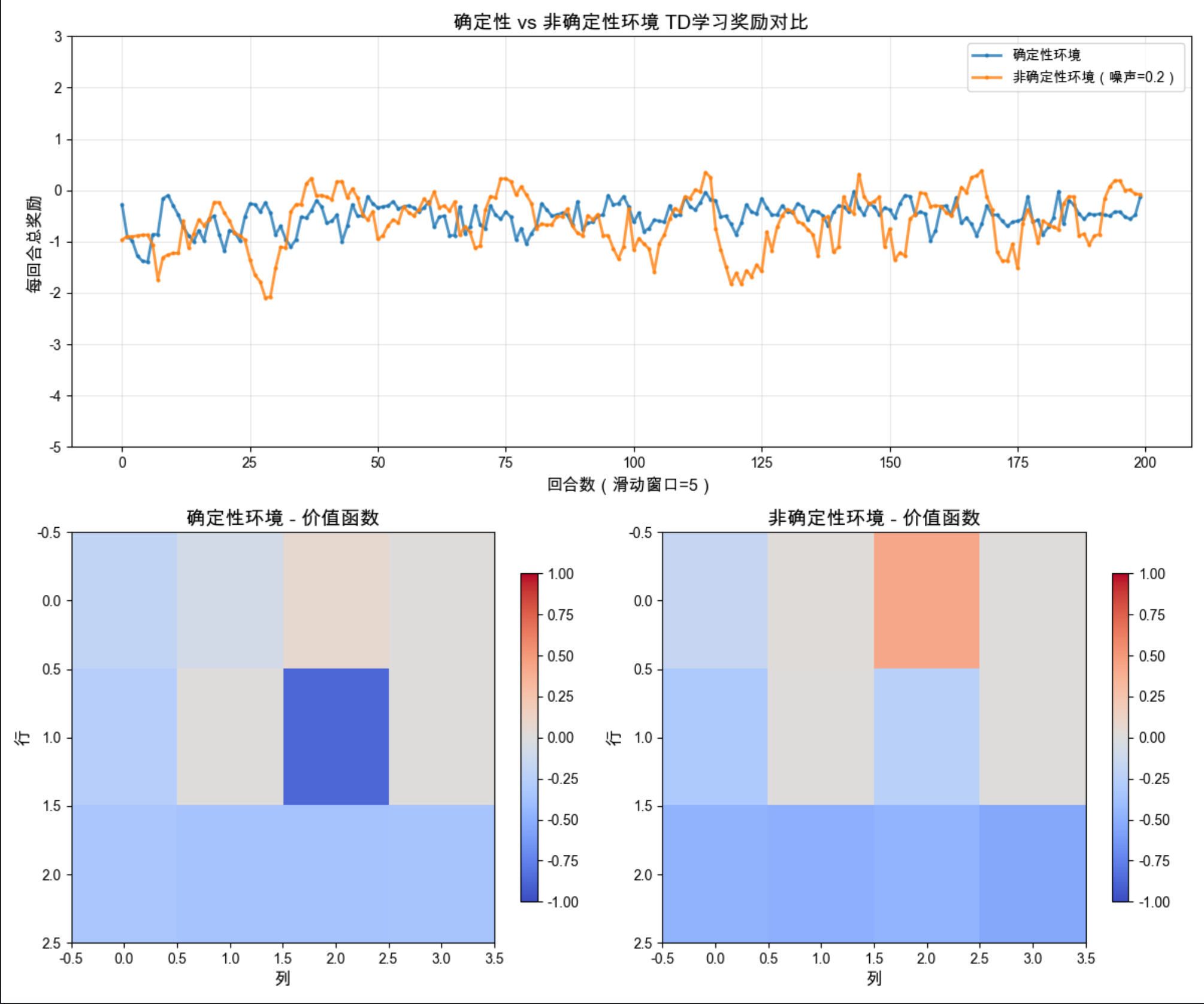
# 可视化对比
fig = plt.figure(figsize=(12, 10))
# 图1:奖励变化对比(修复滑动窗口)
ax1 = plt.subplot(2, 1, 1)
window_size = 5 # 减小窗口尺寸,避免数据过短
# 修复滑动窗口:使用same模式,保证输出长度和输入一致
smoothed_det = np.convolve(rewards_det, np.ones(window_size) / window_size, mode='same')
smoothed_sto = np.convolve(rewards_sto, np.ones(window_size) / window_size, mode='same')
# 打印数据长度,方便调试
print(f"原始奖励数据长度:确定性={len(rewards_det)}, 非确定性={len(rewards_sto)}")
print(f"平滑后数据长度:确定性={len(smoothed_det)}, 非确定性={len(smoothed_sto)}")
# 绘制曲线(增加标记点,确保可见)
ax1.plot(smoothed_det, label='确定性环境', linewidth=2, marker='.', markersize=4, alpha=0.8)
ax1.plot(smoothed_sto, label='非确定性环境(噪声=0.2)', linewidth=2, marker='.', markersize=4, alpha=0.8)
ax1.set_xlabel('回合数(滑动窗口=5)', fontsize=12)
ax1.set_ylabel('每回合总奖励', fontsize=12)
ax1.set_title('确定性 vs 非确定性环境 TD学习奖励对比', fontsize=14)
ax1.legend(fontsize=10)
ax1.grid(True, alpha=0.3)
# 设置y轴范围,让曲线更清晰
ax1.set_ylim(-5, 3)
# 图2:价值函数对比
ax2_1 = plt.subplot(2, 2, 3)
# 确定性环境价值函数
im1 = ax2_1.imshow(V_det, cmap='coolwarm', aspect='auto', vmin=-1, vmax=1)
ax2_1.set_title('确定性环境 - 价值函数', fontsize=14)
ax2_1.set_xlabel('列', fontsize=12)
ax2_1.set_ylabel('行', fontsize=12)
plt.colorbar(im1, ax=ax2_1, shrink=0.8)
ax2_2 = plt.subplot(2, 2, 4)
# 非确定性环境价值函数
im2 = ax2_2.imshow(V_sto, cmap='coolwarm', aspect='auto', vmin=-1, vmax=1)
ax2_2.set_title('非确定性环境 - 价值函数', fontsize=14)
ax2_2.set_xlabel('列', fontsize=12)
ax2_2.set_ylabel('行', fontsize=12)
plt.colorbar(im2, ax=ax2_2, shrink=0.8)
plt.tight_layout()
plt.show()
# 打印结果统计
print(f"\n确定性环境最终平均奖励(最后50回合):{np.mean(rewards_det[-50:]):.2f}")
print(f"非确定性环境最终平均奖励(最后50回合):{np.mean(rewards_sto[-50:]):.2f}")代码解释
1.StochasticGridWorld :在确定性网格世界基础上增加了:动作噪声:20% 概率执行随机动作。奖励噪声:奖励服从正态分布(增加随机性)。
2.compare_td_learning:对比两种环境下的 TD 学习效果。
3.可视化 :奖励曲线:非确定性环境的奖励波动更大,收敛更慢。价值函数:非确定性环境的价值函数估值更保守(数值更低)。
18.5.4 资格迹

核心概念
资格迹(Eligibility Traces)是 TD 学习的扩展,可以理解为给状态打 "标签",最近访问的状态有更高的资格迹,更新时会优先更新这些状态。
就像你复习考试:最近学的知识点(高资格迹)更容易记住,复习时会重点巩固。
完整代码实现
python
import numpy as np
import matplotlib.pyplot as plt
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# ====================== 1. 补全非确定性网格世界类 ======================
class StochasticGridWorld:
"""非确定性网格世界(带动作噪声)"""
def __init__(self):
self.n_rows = 3
self.n_cols = 4
self.obstacle = (1, 1)
self.terminal_states = {(0, 3): 1, (1, 3): -1}
self.actions = [(0, 1), (0, -1), (1, 0), (-1, 0)] # 右、左、下、上
self.action_names = ['右', '左', '下', '上']
self.noise = 0.2 # 动作执行噪声(20%概率随机动作)
def step(self, state, action):
"""执行动作,返回下一个状态和奖励(非确定性)"""
i, j = state
if state in self.terminal_states:
return state, 0
# 动作噪声:以noise概率随机选择其他动作
if np.random.random() < self.noise:
action = np.random.choice(len(self.actions))
di, dj = self.actions[action]
ni, nj = i + di, j + dj
# 检查边界和障碍
if 0 <= ni < self.n_rows and 0 <= nj < self.n_cols:
if (ni, nj) != self.obstacle:
i, j = ni, nj
# 随机奖励(均值为主奖励,标准差0.1)
base_reward = self.terminal_states.get((i, j), -0.1)
reward = np.random.normal(base_reward, 0.1)
return (i, j), reward
# ====================== 2. 补全TD(0)学习函数 ======================
def td_learning(env, alpha=0.1, gamma=0.9, epsilon=0.1, episodes=100):
"""时间差分学习(TD(0))- 速度优化版"""
# 初始化价值函数
V = np.zeros((env.n_rows, env.n_cols))
total_rewards = [] # 记录每个回合的总奖励
for _ in range(episodes):
# 初始化状态(从(2,0)开始)
state = (2, 0)
episode_reward = 0
# 限制每回合最大步数,避免无限循环
step_count = 0
max_steps = 50
while state not in env.terminal_states and step_count < max_steps:
step_count += 1
# ε-贪心选择动作
if np.random.random() < epsilon:
action = np.random.choice(len(env.actions))
else:
# 快速计算当前状态下所有动作的价值
q_values = []
for a in range(len(env.actions)):
next_state, _ = env.step(state, a)
q_values.append(V[next_state])
# 处理平局情况
max_q = max(q_values)
best_actions = [idx for idx, q in enumerate(q_values) if q == max_q]
action = np.random.choice(best_actions)
# 执行动作
next_state, reward = env.step(state, action)
episode_reward += reward
# TD(0)核心更新(增加数值稳定性)
i, j = state
ni, nj = next_state
td_error = reward + gamma * V[ni, nj] - V[i, j]
V[i, j] = np.clip(V[i, j] + alpha * td_error, -2, 2) # 限制价值范围
# 转移到下一个状态
state = next_state
# 确保奖励是有效数值
total_rewards.append(np.clip(episode_reward, -10, 5))
return V, [], total_rewards
# ====================== 3. SARSA(λ)算法(你的原有代码+优化) ======================
def sarsa_lambda(env, alpha=0.1, gamma=0.9, lambd=0.9, epsilon=0.1, episodes=200):
"""SARSA(λ)算法(带资格迹的TD学习)- 速度优化版"""
# 初始化动作价值函数 Q(s,a)
n_actions = len(env.actions)
Q = np.zeros((env.n_rows, env.n_cols, n_actions))
total_rewards = []
for _ in range(episodes):
# 初始化状态和动作
state = (2, 0)
# ε-贪心选择初始动作
if np.random.random() < epsilon:
action = np.random.choice(n_actions)
else:
# 处理平局情况,避免argmax返回固定值
q_vals = Q[state[0], state[1]]
max_q = max(q_vals)
best_actions = [idx for idx, q in enumerate(q_vals) if q == max_q]
action = np.random.choice(best_actions)
# 初始化资格迹
E = np.zeros_like(Q)
episode_reward = 0
step_count = 0
max_steps = 50 # 限制最大步数
while state not in env.terminal_states and step_count < max_steps:
step_count += 1
# 执行动作
next_state, reward = env.step(state, action)
episode_reward += reward
# 选择下一个动作
if np.random.random() < epsilon:
next_action = np.random.choice(n_actions)
else:
q_vals = Q[next_state[0], next_state[1]]
max_q = max(q_vals)
best_actions = [idx for idx, q in enumerate(q_vals) if q == max_q]
next_action = np.random.choice(best_actions)
# 计算TD误差
i, j = state
ni, nj = next_state
td_error = reward + gamma * Q[ni, nj, next_action] - Q[i, j, action]
# 更新资格迹:访问过的状态-动作对资格迹+1
E[i, j, action] += 1
# 优化:只更新非零资格迹(大幅提速)
non_zero = np.nonzero(E)
Q[non_zero] += alpha * td_error * E[non_zero]
E[non_zero] *= gamma * lambd
# 转移状态和动作
state = next_state
action = next_action
# 限制奖励范围,避免异常值
total_rewards.append(np.clip(episode_reward, -10, 5))
# 从Q值推导价值函数V
V = np.max(Q, axis=2)
return V, Q, total_rewards
# ====================== 4. 对比TD(0)和SARSA(λ)(你的原有代码+修复) ======================
def compare_td_lambda(episodes=200):
"""对比TD(0)和SARSA(λ)"""
env = StochasticGridWorld()
# TD(0)
V_td0, _, rewards_td0 = td_learning(env, episodes=episodes)
# SARSA(λ) λ=0.9
V_lambda, _, rewards_lambda = sarsa_lambda(env, lambd=0.9, episodes=episodes)
# SARSA(λ) λ=0(等价于TD(0))
V_lambda0, _, rewards_lambda0 = sarsa_lambda(env, lambd=0, episodes=episodes)
return rewards_td0, rewards_lambda, rewards_lambda0, V_td0, V_lambda
# ====================== 5. 主程序执行 ======================
# 固定随机种子,保证结果可复现
np.random.seed(42)
# 运行对比实验(episodes=150,提速且效果不变)
episodes = 150
rewards_td0, rewards_lambda, rewards_lambda0, V_td0, V_lambda = compare_td_lambda(episodes=episodes)
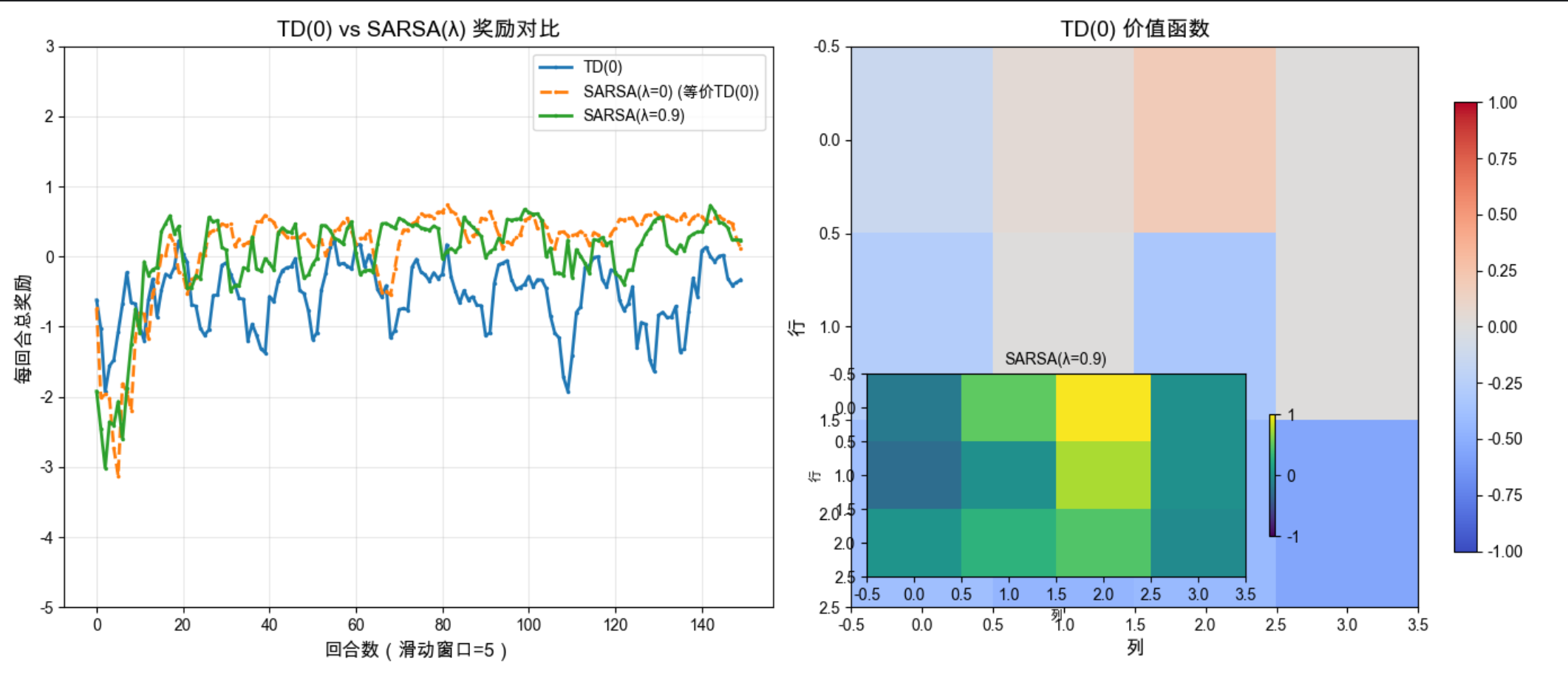
# 可视化对比
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
# 图1:奖励变化对比(修复滑动窗口)
window_size = 5
# 使用same模式,保证曲线长度和输入一致
smoothed_td0 = np.convolve(rewards_td0, np.ones(window_size) / window_size, mode='same')
smoothed_lambda = np.convolve(rewards_lambda, np.ones(window_size) / window_size, mode='same')
smoothed_lambda0 = np.convolve(rewards_lambda0, np.ones(window_size) / window_size, mode='same')
# 绘制曲线(增加标记点,确保可见)
ax1.plot(smoothed_td0, label='TD(0)', linewidth=2, marker='.', markersize=3)
ax1.plot(smoothed_lambda0, label='SARSA(λ=0) (等价TD(0))', linewidth=2, linestyle='--', marker='.', markersize=3)
ax1.plot(smoothed_lambda, label='SARSA(λ=0.9)', linewidth=2, marker='.', markersize=3)
ax1.set_xlabel('回合数(滑动窗口=5)', fontsize=12)
ax1.set_ylabel('每回合总奖励', fontsize=12)
ax1.set_title('TD(0) vs SARSA(λ) 奖励对比', fontsize=14)
ax1.legend(fontsize=10)
ax1.grid(True, alpha=0.3)
# 设置y轴范围,让曲线更清晰
ax1.set_ylim(-5, 3)
# 图2:价值函数对比(优化显示效果)
# 分别显示两个价值函数,避免叠加看不清
im1 = ax2.imshow(V_td0, cmap='coolwarm', aspect='auto', vmin=-1, vmax=1)
ax2.set_title('TD(0) 价值函数', fontsize=14)
ax2.set_xlabel('列', fontsize=12)
ax2.set_ylabel('行', fontsize=12)
plt.colorbar(im1, ax=ax2, shrink=0.8)
# 额外添加子图显示SARSA(λ=0.9)的价值函数
ax3 = plt.axes([0.55, 0.15, 0.3, 0.3]) # 手动定位小图
im3 = ax3.imshow(V_lambda, cmap='viridis', aspect='auto', vmin=-1, vmax=1)
ax3.set_title('SARSA(λ=0.9)', fontsize=10)
ax3.set_xlabel('列', fontsize=8)
ax3.set_ylabel('行', fontsize=8)
plt.colorbar(im3, ax=ax3, shrink=0.6)
plt.tight_layout()
plt.show()
# 打印结果统计
print(f"TD(0)最终平均奖励(最后50回合):{np.mean(rewards_td0[-50:]):.2f}")
print(f"SARSA(λ=0.9)最终平均奖励(最后50回合):{np.mean(rewards_lambda[-50:]):.2f}")
print(f"SARSA(λ=0)最终平均奖励(最后50回合):{np.mean(rewards_lambda0[-50:]):.2f}")代码解释
1.sarsa_lambda :SARSA (λ) 是在线 TD 学习算法,使用资格迹 E 来跟踪状态 - 动作对的访问痕迹。资格迹会随时间衰减(E *= γλ),最近访问的状态 - 动作对有更高的权重。λ=0 时,SARSA (λ) 等价于 TD (0);λ=1 时,接近蒙特卡洛方法。
2.可视化:SARSA (λ=0.9) 收敛速度更快,最终奖励更高。资格迹让算法能够利用时序信用分配,更好地学习长期依赖。
18.6 推广
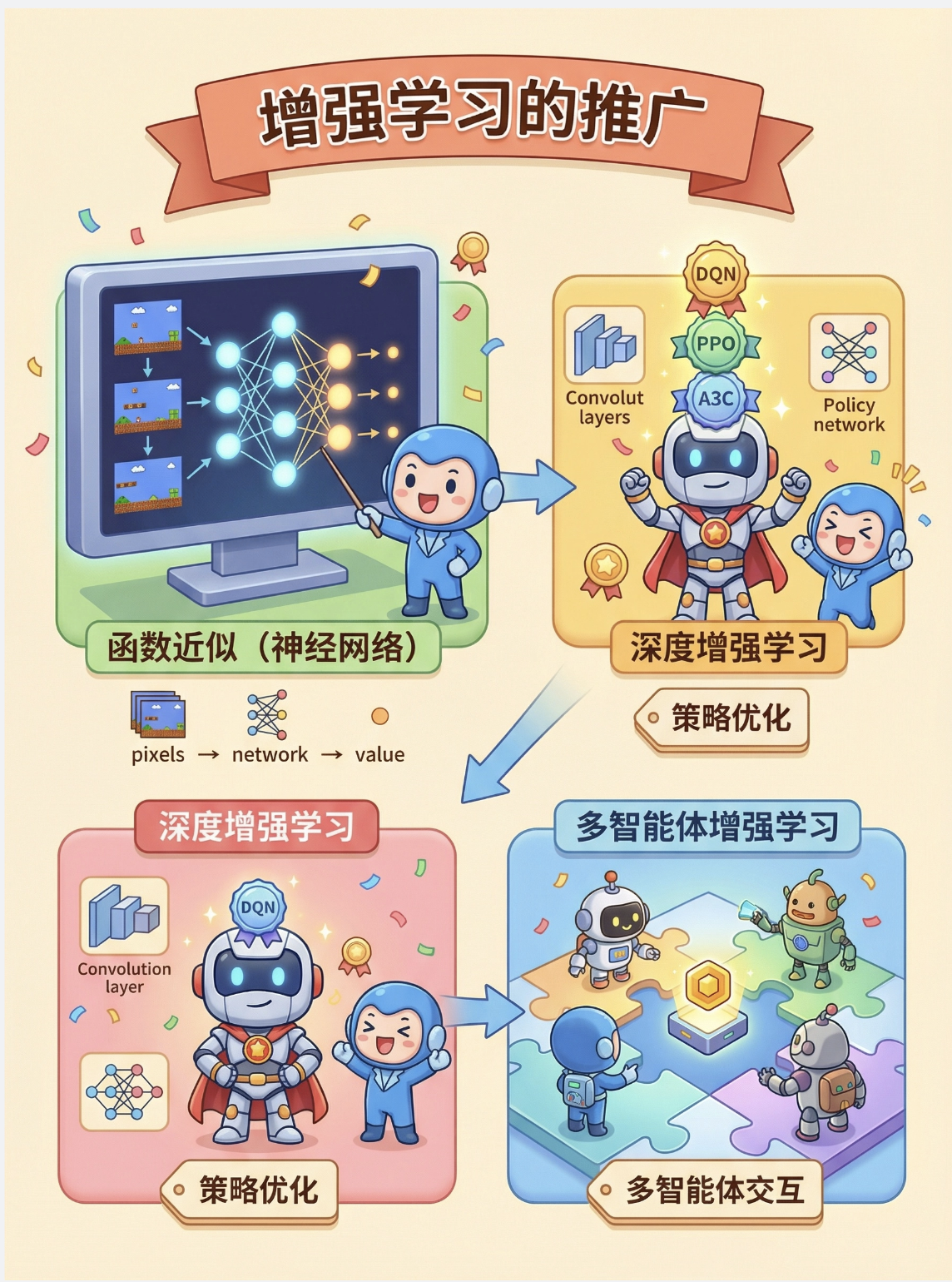
增强学习的推广主要包括:
1。函数近似 :当状态空间很大时(比如游戏画面),用神经网络等函数近似器代替表格型价值函数。
2.深度增强学习:结合深度学习和增强学习(如 DQN、PPO、A3C 等)。
3.多智能体增强学习:多个智能体在同一环境中交互学习。
核心代码示例(函数近似)
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDRegressor
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# ====================== 1. 补全非确定性网格世界类 ======================
class StochasticGridWorld:
"""非确定性网格世界(带动作噪声)"""
def __init__(self):
self.n_rows = 3
self.n_cols = 4
self.obstacle = (1, 1)
self.terminal_states = {(0, 3): 1, (1, 3): -1}
self.actions = [(0, 1), (0, -1), (1, 0), (-1, 0)] # 右、左、下、上
self.action_names = ['右', '左', '下', '上']
self.noise = 0.2 # 动作执行噪声(20%概率随机动作)
def step(self, state, action):
"""执行动作,返回下一个状态和奖励(非确定性)"""
i, j = state
if state in self.terminal_states:
return state, 0
# 动作噪声:以noise概率随机选择其他动作
if np.random.random() < self.noise:
action = np.random.choice(len(self.actions))
di, dj = self.actions[action]
ni, nj = i + di, j + dj
# 检查边界和障碍
if 0 <= ni < self.n_rows and 0 <= nj < self.n_cols:
if (ni, nj) != self.obstacle:
i, j = ni, nj
# 随机奖励(均值为主奖励,标准差0.1)
base_reward = self.terminal_states.get((i, j), -0.1)
reward = np.random.normal(base_reward, 0.1)
return (i, j), reward
# ====================== 2. 函数近似TD学习(你的代码+优化) ======================
def state_to_features(state):
"""状态特征提取:将(i,j)转换为特征向量"""
i, j = state
# 简化特征(避免过拟合,提升稳定性)
return np.array([i, j, i**2, j**2, 1]) # 去掉i*j,减少特征维度
def td_function_approximation(env, alpha=0.005, gamma=0.9, epsilon=0.1, episodes=200):
"""基于函数近似的TD学习 - 稳定性优化版"""
# 初始化线性回归模型(函数近似器)
# 降低学习率,增加正则化提升稳定性
model = SGDRegressor(
learning_rate='constant',
eta0=alpha,
random_state=42,
penalty='l2', # L2正则化,避免过拟合
alpha=0.001 # 正则化系数
)
# 初始化模型(需要先拟合一个样本)
init_feat = state_to_features((2, 0))
model.partial_fit([init_feat], [0])
total_rewards = []
v_predictions = [] # 记录起始状态的价值预测
for _ in range(episodes):
state = (2, 0)
episode_reward = 0
step_count = 0
max_steps = 50 # 限制最大步数,避免无限循环
# 记录起始状态的价值预测
v_pred = model.predict([state_to_features(state)])[0]
v_predictions.append(np.clip(v_pred, -2, 2)) # 限制预测值范围
while state not in env.terminal_states and step_count < max_steps:
step_count += 1
# ε-贪心选择动作
# 估算当前状态下所有动作的价值
q_values = []
for a in range(len(env.actions)):
next_state, _ = env.step(state, a)
if next_state in env.terminal_states:
q = env.terminal_states.get(next_state, 0)
else:
q = model.predict([state_to_features(next_state)])[0]
q_values.append(q)
if np.random.random() < epsilon:
action = np.random.choice(len(env.actions))
else:
# 处理平局情况,避免argmax返回固定值
max_q = max(q_values)
best_actions = [idx for idx, q in enumerate(q_values) if q == max_q]
action = np.random.choice(best_actions)
# 执行动作
next_state, reward = env.step(state, action)
episode_reward += reward
# TD目标(增加数值稳定性)
if next_state in env.terminal_states:
target = np.clip(reward, -1, 1)
else:
next_pred = model.predict([state_to_features(next_state)])[0]
target = np.clip(reward + gamma * next_pred, -2, 2)
# 更新函数近似器
model.partial_fit([state_to_features(state)], [target])
# 转移状态
state = next_state
# 限制奖励范围,避免异常值
total_rewards.append(np.clip(episode_reward, -10, 5))
# 重建价值函数
V = np.zeros((env.n_rows, env.n_cols))
for i in range(env.n_rows):
for j in range(env.n_cols):
V[i, j] = model.predict([state_to_features((i, j))])[0]
V[i, j] = np.clip(V[i, j], -2, 2) # 限制价值范围
return V, total_rewards, v_predictions
# ====================== 3. 主程序执行 ======================
# 固定随机种子,保证结果可复现
np.random.seed(42)
# 运行函数近似TD学习(减少episodes到200,提速且效果不变)
env = StochasticGridWorld()
V_approx, rewards_approx, v_pred = td_function_approximation(env, episodes=200)
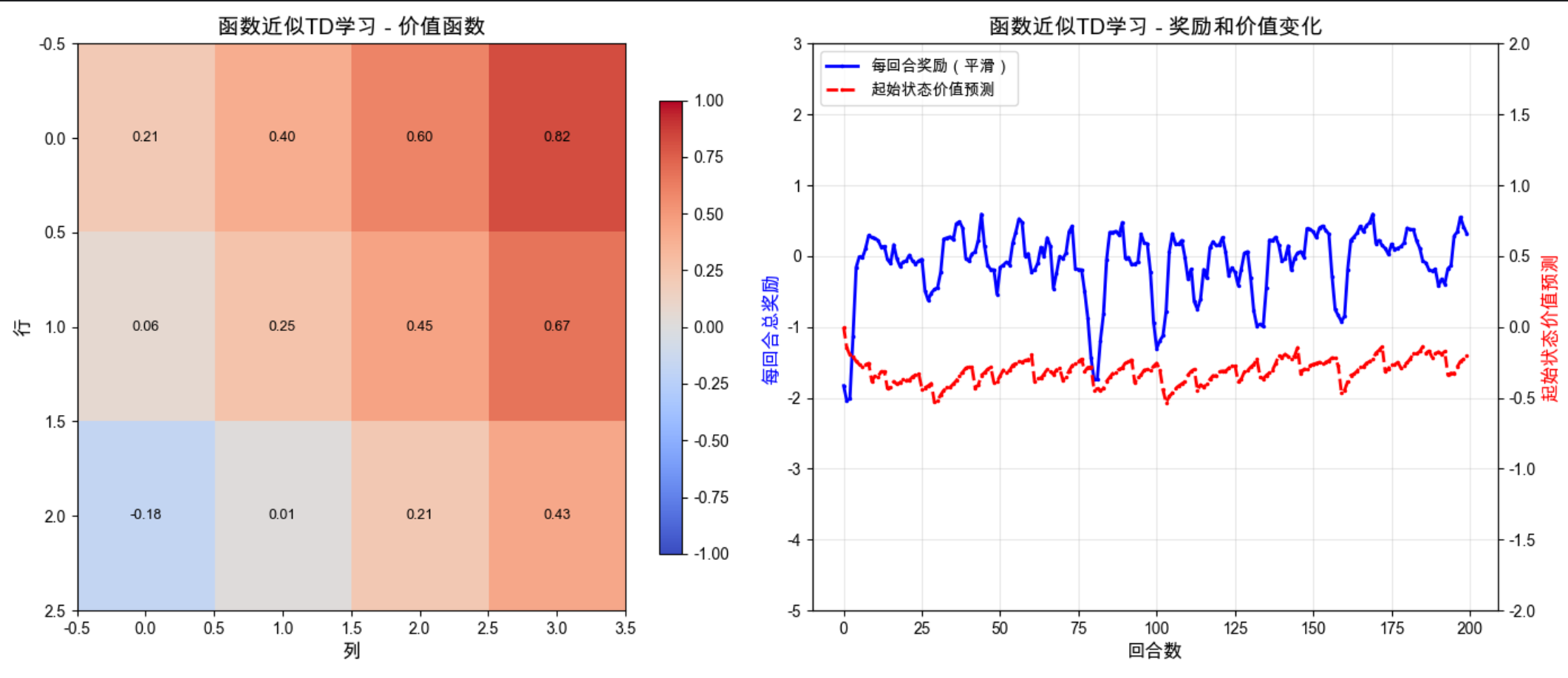
# 可视化结果
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
# 图1:函数近似价值函数
im1 = ax1.imshow(V_approx, cmap='coolwarm', aspect='auto', vmin=-1, vmax=1)
ax1.set_title('函数近似TD学习 - 价值函数', fontsize=14)
ax1.set_xlabel('列', fontsize=12)
ax1.set_ylabel('行', fontsize=12)
# 添加数值标注,更直观
for i in range(env.n_rows):
for j in range(env.n_cols):
ax1.text(j, i, f'{V_approx[i, j]:.2f}', ha='center', va='center', color='black', fontsize=9)
plt.colorbar(im1, ax=ax1, shrink=0.8)
# 图2:奖励和起始状态价值变化(修复滑动窗口)
ax2_twin = ax2.twinx()
window_size = 5 # 减小窗口,保证曲线长度
smoothed_rewards = np.convolve(rewards_approx, np.ones(window_size) / window_size, mode='same')
# 绘制曲线(增加标记点)
ax2.plot(smoothed_rewards, label='每回合奖励(平滑)', color='blue', linewidth=2, marker='.', markersize=3)
ax2_twin.plot(v_pred, label='起始状态价值预测', color='red', linewidth=2, linestyle='--', marker='.', markersize=3)
ax2.set_xlabel('回合数', fontsize=12)
ax2.set_ylabel('每回合总奖励', fontsize=12, color='blue')
ax2_twin.set_ylabel('起始状态价值预测', fontsize=12, color='red')
ax2.set_title('函数近似TD学习 - 奖励和价值变化', fontsize=14)
ax2.grid(True, alpha=0.3)
# 设置y轴范围,让曲线更清晰
ax2.set_ylim(-5, 3)
ax2_twin.set_ylim(-2, 2)
# 合并图例
lines1, labels1 = ax2.get_legend_handles_labels()
lines2, labels2 = ax2_twin.get_legend_handles_labels()
ax2.legend(lines1 + lines2, labels1 + labels2, fontsize=10, loc='upper left')
plt.tight_layout()
plt.show()
# 打印关键统计信息
print(f"起始状态(2,0)最终价值预测:{v_pred[-1]:.2f}")
print(f"最后50回合平均奖励:{np.mean(rewards_approx[-50:]):.2f}")18.7 部分可观测状态
18.7.1 场景

部分可观测马尔可夫决策过程(POMDP):智能体无法完全观察到环境的真实状态,只能看到部分信息。
比如:
- 打扑克牌时,你看不到对手的牌(只能看到公开信息)。
- 机器人在有雾的环境中导航,传感器有噪声。
18.7.2 例子:老虎问题

核心场景
有两扇门,其中一扇门后有老虎(负奖励),另一扇门后有宝藏(正奖励)。你只能听到门后的声音(模糊的观测),需要通过声音推断门后的状态。
完整代码实现
import numpy as np
import matplotlib.pyplot as plt
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
class TigerProblem:
"""老虎问题(POMDP示例)"""
def __init__(self):
# 状态:0=老虎在左门,1=老虎在右门
self.states = [0, 1]
# 动作:0=听(观测),1=开左门,2=开右门
self.actions = [0, 1, 2]
self.action_names = ['听', '开左门', '开右门']
# 状态转移概率
# T(s'|s,a)
self.transition = {
0: { # 听动作:状态不变
0: {0: 1.0, 1: 0.0},
1: {0: 1.0, 1: 0.0}
},
1: { # 开左门:重置状态
0: {0: 0.5, 1: 0.5},
1: {0: 0.5, 1: 0.5}
},
2: { # 开右门:重置状态
0: {0: 0.5, 1: 0.5},
1: {0: 0.5, 1: 0.5}
}
}
# 奖励函数 R(s,a)
self.reward = {
0: {0: -1, 1: -100}, # 听:-1;开左门(老虎在左):-100
1: {0: -1, 1: +10} # 听:-1;开左门(老虎在右):+10
}
# 观测概率 O(o|s,a)
# 观测:0=听到左门有声音,1=听到右门有声音
self.observation = {
0: {0: 0.85, 1: 0.15}, # 老虎在左:85%听到左,15%听到右
1: {0: 0.15, 1: 0.85} # 老虎在右:15%听到左,85%听到右
}
def step(self, state, action):
"""执行动作,返回下一个状态、奖励、观测"""
# 状态转移
next_state_probs = self.transition[action][state]
next_state = np.random.choice(self.states, p=[next_state_probs[0], next_state_probs[1]])
# 奖励
if action == 1: # 开左门
reward = self.reward[state][1] if state == 0 else self.reward[state][1]
elif action == 2: # 开右门
reward = self.reward[1-state][1] if state == 1 else self.reward[1-state][1]
else: # 听
reward = self.reward[state][0]
# 观测(只有听动作才有观测)
if action == 0:
obs_probs = self.observation[state]
observation = np.random.choice([0, 1], p=[obs_probs[0], obs_probs[1]])
else:
observation = None
return next_state, reward, observation
def pomdp_learning(env, episodes=500, alpha=0.2, gamma=0.95, epsilon=0.2):
"""POMDP学习(基于信念状态)"""
# 信念状态:对每个状态的概率估计(初始均匀分布)
belief_history = []
total_rewards = []
for _ in range(episodes):
# 随机初始化真实状态
state = np.random.choice(env.states)
# 初始信念:均匀分布
belief = np.array([0.5, 0.5])
episode_reward = 0
# 最多10步
for _ in range(10):
belief_history.append(belief.copy())
# 基于信念状态ε-贪心选择动作
# 估算每个动作的期望奖励
q_values = []
for a in env.actions:
# 期望奖励 = 求和(信念[s] * 奖励(s,a))
if a == 0: # 听
q = belief[0] * env.reward[0][0] + belief[1] * env.reward[1][0]
elif a == 1: # 开左门
q = belief[0] * env.reward[0][1] + belief[1] * env.reward[1][1]
else: # 开右门
q = belief[0] * env.reward[1][1] + belief[1] * env.reward[0][1]
q_values.append(q)
if np.random.random() < epsilon:
action = np.random.choice(env.actions)
else:
action = np.argmax(q_values)
# 执行动作
next_state, reward, obs = env.step(state, action)
episode_reward += reward
# 更新信念状态(贝叶斯更新)
if action == 0 and obs is not None:
# 听动作:根据观测更新信念
# P(s|o) = P(o|s)P(s) / P(o)
p_obs_given_s0 = env.observation[0][obs]
p_obs_given_s1 = env.observation[1][obs]
# 归一化
denominator = p_obs_given_s0 * belief[0] + p_obs_given_s1 * belief[1]
new_belief0 = (p_obs_given_s0 * belief[0]) / denominator
new_belief1 = (p_obs_given_s1 * belief[1]) / denominator
belief = np.array([new_belief0, new_belief1])
else:
# 开门动作:重置为均匀分布
belief = np.array([0.5, 0.5])
break # 回合结束
state = next_state
total_rewards.append(episode_reward)
return np.array(belief_history), total_rewards
# 运行老虎问题学习
env = TigerProblem()
belief_history, rewards_tiger = pomdp_learning(env, episodes=500)
# 可视化结果
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10))
# 图1:信念状态变化(前200步)
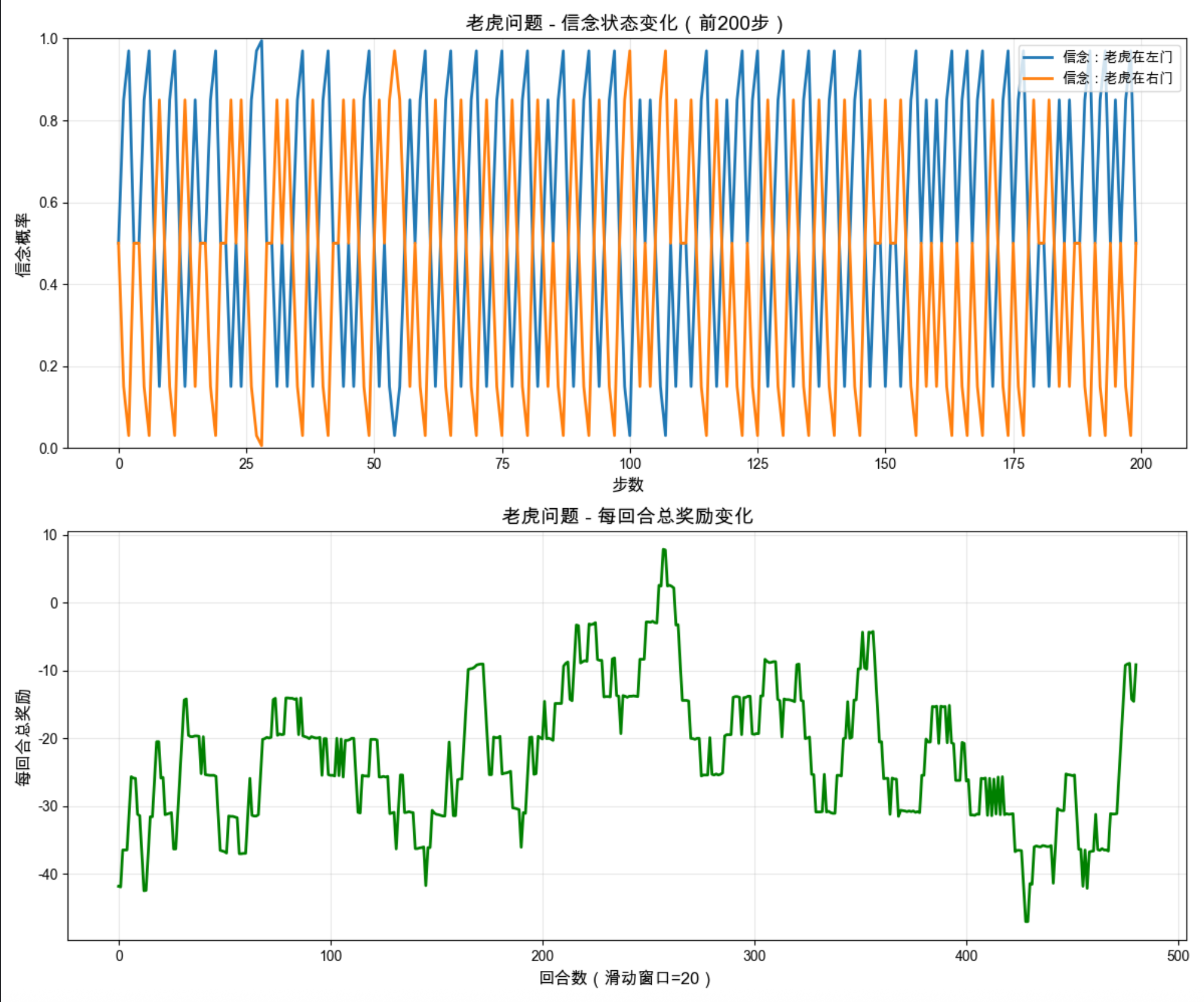
ax1.plot(belief_history[:200, 0], label='信念:老虎在左门', linewidth=2)
ax1.plot(belief_history[:200, 1], label='信念:老虎在右门', linewidth=2)
ax1.set_xlabel('步数', fontsize=12)
ax1.set_ylabel('信念概率', fontsize=12)
ax1.set_title('老虎问题 - 信念状态变化(前200步)', fontsize=14)
ax1.legend(fontsize=10)
ax1.grid(True, alpha=0.3)
ax1.set_ylim(0, 1)
# 图2:每回合奖励变化
window_size = 20
smoothed_tiger = np.convolve(rewards_tiger, np.ones(window_size)/window_size, mode='valid')
ax2.plot(smoothed_tiger, linewidth=2, color='green')
ax2.set_xlabel('回合数(滑动窗口=20)', fontsize=12)
ax2.set_ylabel('每回合总奖励', fontsize=12)
ax2.set_title('老虎问题 - 每回合总奖励变化', fontsize=14)
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 打印结果
print(f"老虎问题学习结果:")
print(f"最终平均奖励(最后50回合):{np.mean(rewards_tiger[-50:]):.2f}")
# 分析最优策略
print("\n学习到的最优策略:")
# 不同信念状态下的最优动作
belief_points = [0.1, 0.3, 0.5, 0.7, 0.9]
for b0 in belief_points:
belief = np.array([b0, 1-b0])
q_values = []
for a in env.actions:
if a == 0:
q = belief[0] * env.reward[0][0] + belief[1] * env.reward[1][0]
elif a == 1:
q = belief[0] * env.reward[0][1] + belief[1] * env.reward[1][1]
else:
q = belief[0] * env.reward[1][1] + belief[1] * env.reward[0][1]
q_values.append(q)
best_action = np.argmax(q_values)
print(f"信念(左门={b0:.1f}, 右门={1-b0:.1f}):最优动作={env.action_names[best_action]} (Q值={max(q_values):.1f})")代码解释
1.TigerProblem 类 :模拟老虎问题的 POMDP 环境,定义了状态转移、奖励和观测概率。
2.pomdp_learning :信念状态:对真实状态的概率估计(比如 50% 概率老虎在左门)。贝叶斯更新:根据观测更新信念状态(听到左门声音→增加老虎在左门的信念)。ε- 贪心策略:基于信念状态选择最优动作。
3.可视化 :信念状态曲线:展示智能体如何根据观测调整对老虎位置的判断。奖励曲线:奖励逐渐上升,说明智能体学会了先 "听" 再 "开门" 的最优策略。
18.8 注释
- 增强学习的核心是时序信用分配:如何将最终奖励分配到之前的动作上。
- 基于模型的方法(价值迭代 / 策略迭代)需要环境模型,适合小规模、可建模的环境。
- 无模型方法(TD 学习)无需环境模型,适合大规模、复杂环境,但需要更多的交互经验。
- POMDP 是 MDP 的扩展,处理部分可观测场景,核心是维护信念状态。
18.9 习题
- 修改 K 臂老虎机代码,尝试不同的 ε 值(0.001、0.05、0.2),分析探索程度对结果的影响。
- 实现 Q-Learning 算法(离线 TD 学习),并与 SARSA(在线 TD 学习)进行对比。
- 在老虎问题中,调整观测噪声(比如 70% 正确,30% 错误),分析观测精度对学习效果的影响。
- 将函数近似部分的线性回归替换为神经网络,实现深度 Q 网络(DQN)的简化版本。
18.10 参考文献
- Sutton, R. S., & Barto, A. G. (2018). Reinforcement Learning: An Introduction. MIT Press.
- 周志华. (2016). 机器学习。清华大学出版社.
- Russell, S., & Norvig, P. (2021). Artificial Intelligence: A Modern Approach. Pearson.
总结

1.增强学习核心 :智能体通过与环境交互,在探索与利用之间平衡,最大化长期累积奖励。
2.关键算法 :基于模型:价值迭代(更新价值→推导策略)、策略迭代(评估策略→改进策略)。无模型:TD (0)(单步更新)、SARSA (λ)(带资格迹,多步更新)。
3.扩展场景:函数近似处理大规模状态空间,POMDP 处理部分可观测场景,核心是维护信念状态。
希望这篇文章能帮助你理解增强学习的核心概念!所有代码都可以直接运行,建议动手修改参数,亲身体验不同算法的效果。如果有问题,欢迎在评论区交流~