《计算机视觉：模型、学习和推理》第 2 章-概率概述

import numpy as np
import matplotlib.pyplot as plt
import cv2

# ==================== Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 1. 离散随机变量：模拟骰子投掷（计算机视觉中可类比"像素类别预测"）
def discrete_random_variable():
    # 模拟投掷1000次骰子
    dice_rolls = np.random.randint(1, 7, size=1000)
    # 统计每个点数出现的次数
    counts = np.bincount(dice_rolls)[1:]  # 去掉0的计数
    probabilities = counts / len(dice_rolls)  # 计算频率（近似概率）
    
    # 可视化
    plt.figure(figsize=(8, 5))
    plt.bar(range(1,7), probabilities, color='skyblue', edgecolor='black')
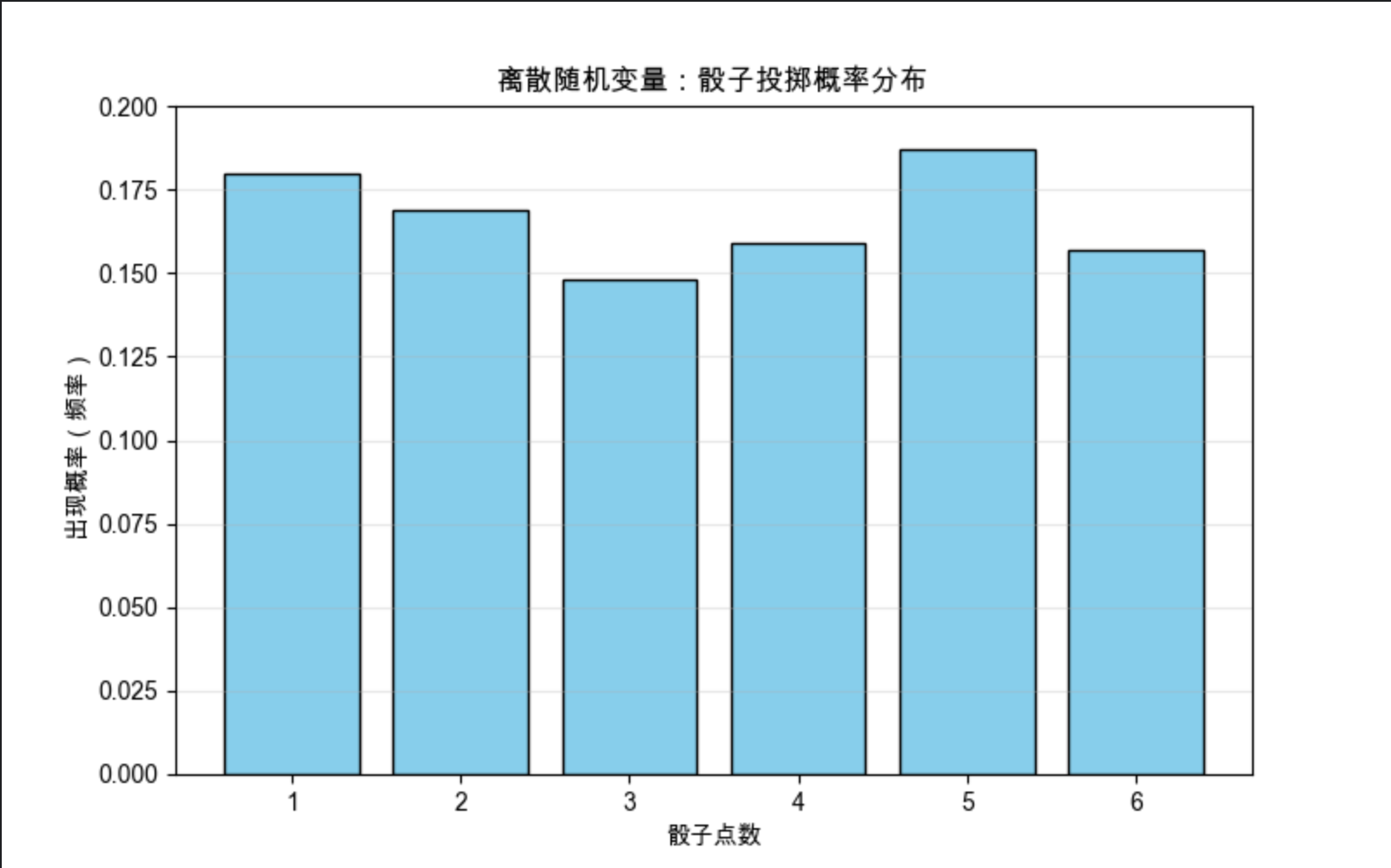
    plt.title('离散随机变量：骰子投掷概率分布', fontsize=12)
    plt.xlabel('骰子点数', fontsize=10)
    plt.ylabel('出现概率（频率）', fontsize=10)
    plt.xticks(range(1,7))
    plt.ylim(0, 0.2)
    plt.grid(axis='y', alpha=0.3)
    return dice_rolls

# 2. 连续随机变量：模拟图像像素亮度（0-255）
def continuous_random_variable():
    # 生成符合正态分布的像素亮度值（模拟自然图像的亮度分布）
    pixel_brightness = np.random.normal(loc=128, scale=32, size=10000)
    # 限制在0-255范围内（符合像素值物理意义）
    pixel_brightness = np.clip(pixel_brightness, 0, 255)
    
    # 可视化
    plt.figure(figsize=(8, 5))
    plt.hist(pixel_brightness, bins=50, density=True, color='orange', alpha=0.7, edgecolor='black')
    plt.title('连续随机变量：图像像素亮度概率分布', fontsize=12)
    plt.xlabel('像素亮度值', fontsize=10)
    plt.ylabel('概率密度', fontsize=10)
    plt.xlim(0, 255)
    plt.grid(axis='y', alpha=0.3)
    return pixel_brightness

# 运行并可视化
dice_data = discrete_random_variable()
plt.show()
brightness_data = continuous_random_variable()
plt.show()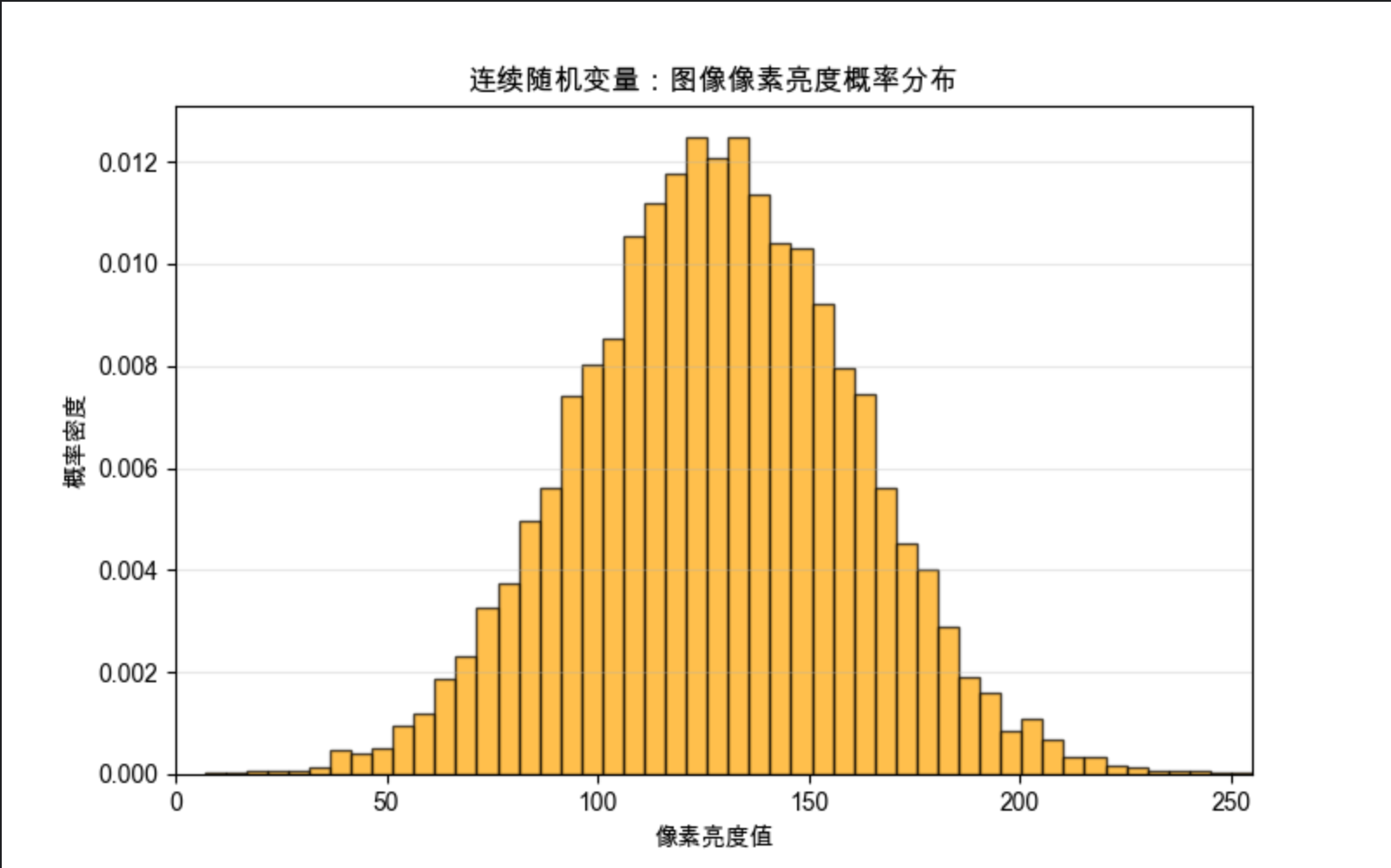

效果说明

离散随机变量图：骰子每个点数的出现概率接近 1/6，符合均匀分布特性；
连续随机变量图：像素亮度呈正态分布（自然图像中大部分像素亮度集中在中间值）。

2.2 联合概率

核心概念

联合概率是 "多个随机变量同时发生的概率"，比如：

类比：图像中 "像素 A 是红色（变量 1）" 且 "像素 A 的亮度 > 200（变量 2）" 的概率

可以理解为 "两个盒子同时打开，各自出现某个结果的概率"。

代码实现 + 可视化（图像双特征联合分布）

python 复制代码

# 导入所有必要的库
import numpy as np
import matplotlib.pyplot as plt

# ==================== Mac系统Matplotlib中文显示配置 ====================
# 适配Mac系统的中文字体，解决负号显示问题
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

def joint_probability():
    # 生成模拟数据：图像中1000个像素的两个特征
    # 特征1：是否为红色像素（0=否，1=是）
    is_red = np.random.binomial(n=1, p=0.3, size=1000)
    # 特征2：像素亮度值（0-255）
    brightness = np.random.normal(loc=150, scale=40, size=1000)
    brightness = np.clip(brightness, 0, 255)
    
    # 计算联合概率：红色像素且亮度>200的概率
    red_and_bright = np.logical_and(is_red == 1, brightness > 200)
    joint_prob = np.sum(red_and_bright) / len(is_red)
    
    # 可视化联合分布
    plt.figure(figsize=(10, 6))
    
    # 子图1：散点图展示两个变量的联合分布
    plt.subplot(1,2,1)
    plt.scatter(is_red, brightness, alpha=0.6, c=brightness, cmap='Reds')
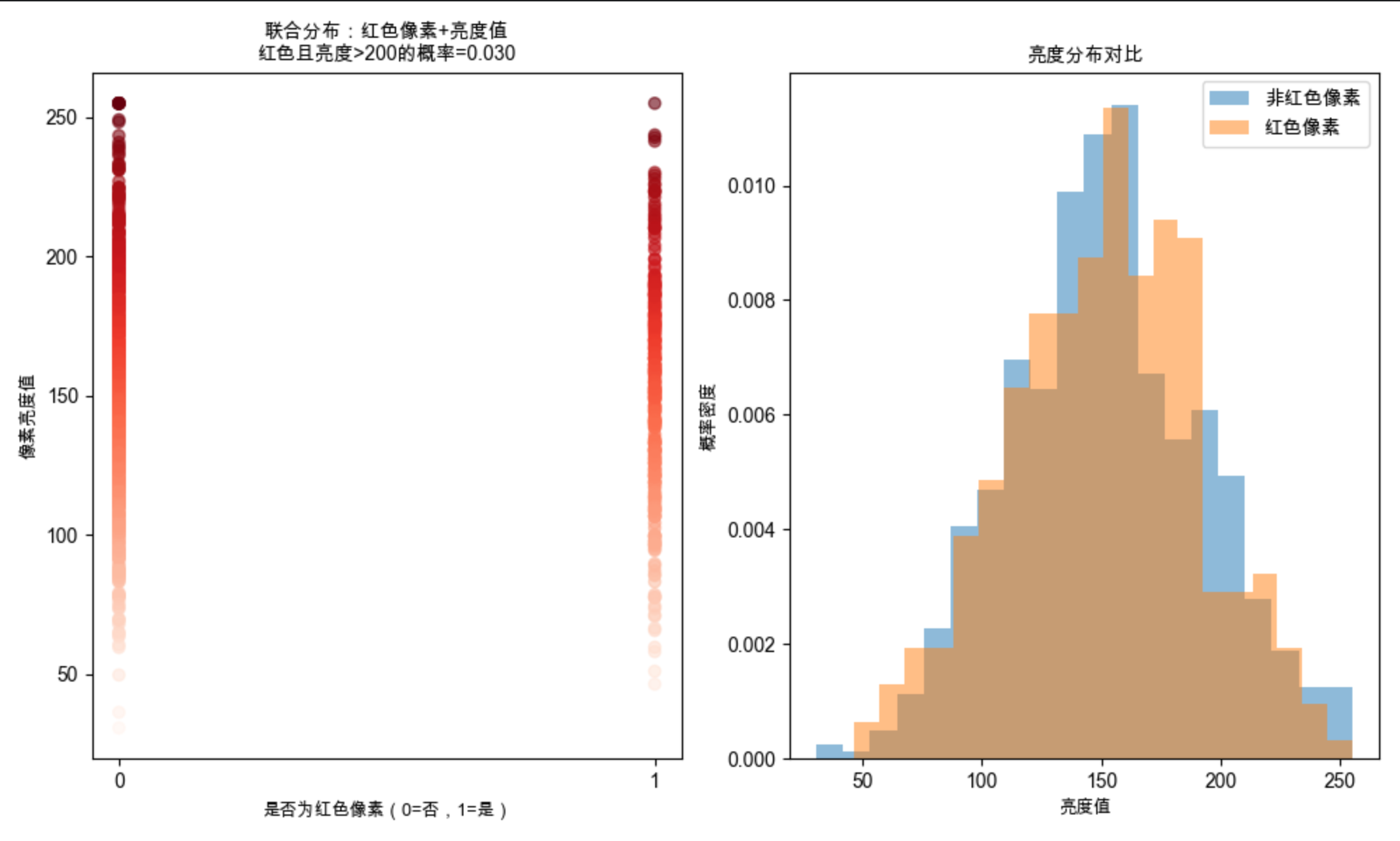
    plt.title(f'联合分布：红色像素+亮度值\n红色且亮度>200的概率={joint_prob:.3f}', fontsize=10)
    plt.xlabel('是否为红色像素（0=否，1=是）', fontsize=9)
    plt.ylabel('像素亮度值', fontsize=9)
    plt.xticks([0,1])
    
    # 子图2：分组统计
    plt.subplot(1,2,2)
    # 非红色像素亮度分布
    non_red_bright = brightness[is_red == 0]
    # 红色像素亮度分布
    red_bright = brightness[is_red == 1]
    plt.hist(non_red_bright, bins=20, alpha=0.5, label='非红色像素', density=True)
    plt.hist(red_bright, bins=20, alpha=0.5, label='红色像素', density=True)
    plt.title('亮度分布对比', fontsize=10)
    plt.xlabel('亮度值', fontsize=9)
    plt.ylabel('概率密度', fontsize=9)
    plt.legend()
    
    plt.tight_layout()
    plt.show()
    return joint_prob

# 主程序运行入口
if __name__ == "__main__":
    # 调用函数并获取结果
    joint_prob = joint_probability()
    # 打印计算得到的联合概率
    print(f"红色像素且亮度>200的联合概率：{joint_prob:.3f}")

效果说明

散点图直观展示 "是否红色" 和 "亮度" 两个变量的联合分布；
分组直方图对比了红色 / 非红色像素的亮度分布差异，体现联合概率的实际意义。

2.3 边缘化

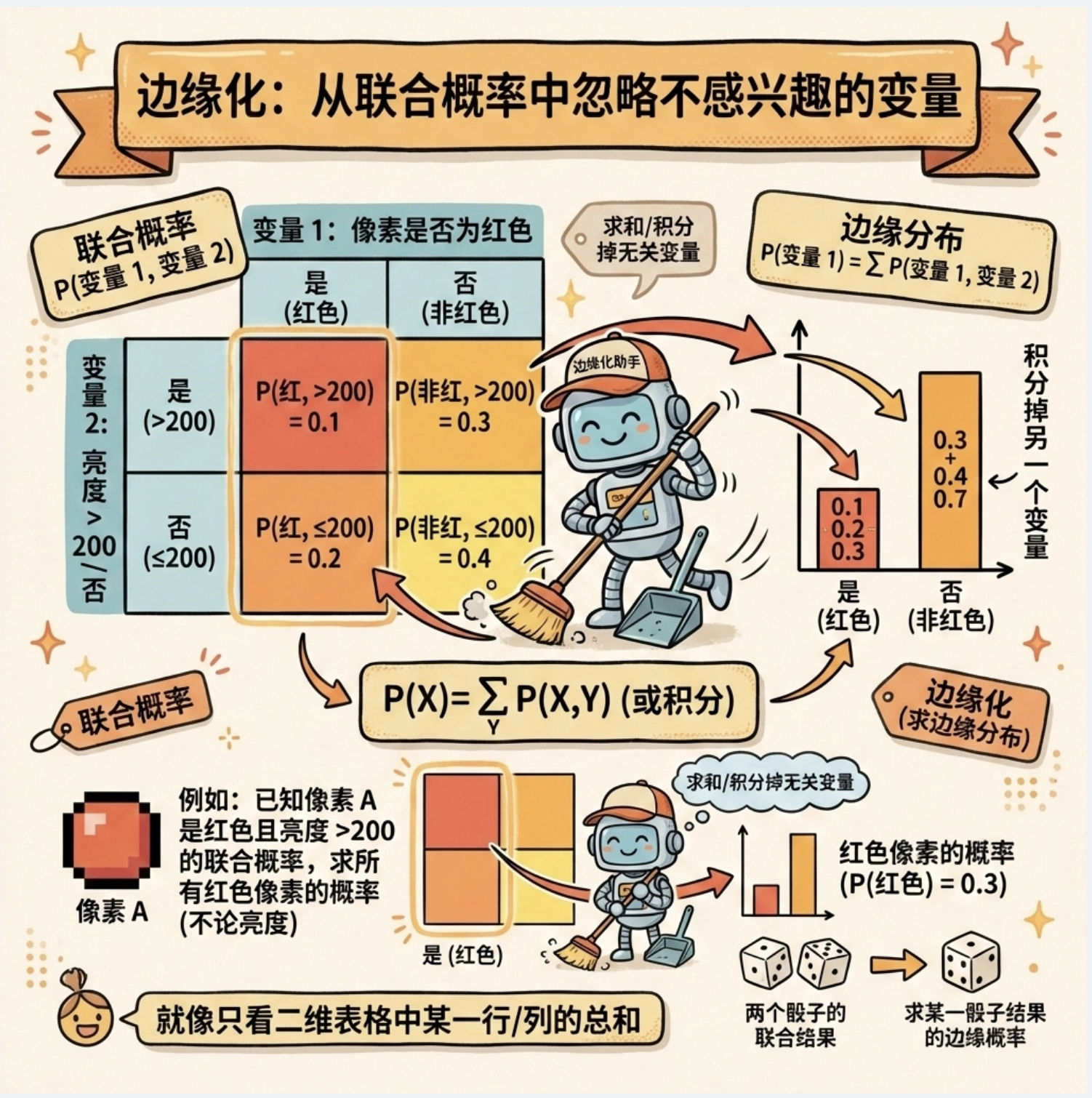
核心概念

边缘化是 "从联合概率中忽略某个变量，只关注我们关心的变量"，比如：

类比：知道 "像素 A 是红色且亮度> 200" 的联合概率，想求 "所有红色像素的概率"（不管亮度）

核心逻辑：把不需要的变量 "加起来 / 积分掉"，就像从 "二维表格" 中只看 "一行 / 一列" 的总和。

代码实现 + 可视化（图像特征边缘化）

python 复制代码

# 导入运行所需的全部库
import numpy as np
import matplotlib.pyplot as plt

# ==================== Mac系统Matplotlib中文显示专属配置 ====================
# 解决Mac下中文显示乱码、负号显示异常问题
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定Mac兼容中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 优化画布背景显示效果

def marginalization():
    # 生成模拟数据：1000个像素的3个特征（是否红色、是否绿色、亮度）
    n = 1000
    # 特征1：是否为红色像素（0=否，1=是），概率0.25
    is_red = np.random.binomial(1, 0.25, n)
    # 特征2：是否为绿色像素（0=否，1=是），概率0.2
    is_green = np.random.binomial(1, 0.2, n)
    # 特征3：像素亮度值（正态分布，均值128，标准差30，限制在0-255）
    brightness = np.random.normal(128, 30, n)
    brightness = np.clip(brightness, 0, 255)  # 确保亮度值符合像素物理范围
    
    # 1. 计算3变量联合概率：同时满足「红色+绿色+亮度>150」的概率
    joint_3d = np.logical_and.reduce([is_red==1, is_green==1, brightness>150])
    joint_3d_prob = np.sum(joint_3d) / n  # 频率近似概率
    
    # 2. 第一次边缘化：忽略绿色变量，计算「红色+亮度>150」的2变量边缘概率
    marginal_2d = np.logical_and(is_red==1, brightness>150)
    marginal_2d_prob = np.sum(marginal_2d) / n
    
    # 3. 第二次边缘化：忽略绿色+亮度，仅计算「红色像素」的1变量边缘概率
    marginal_1d = is_red == 1
    marginal_1d_prob = np.sum(marginal_1d) / n
    
    # 可视化：对比3维联合分布→2维边缘分布→1维边缘分布的过程
    plt.figure(figsize=(12, 4))  # 设置画布大小，适配多子图显示
    
    # 子图1：3变量联合分布（x=是否红色，y=是否绿色，颜色=亮度值）
    plt.subplot(1,3,1)
    plt.scatter(is_red, is_green, c=brightness, cmap='viridis', alpha=0.7)
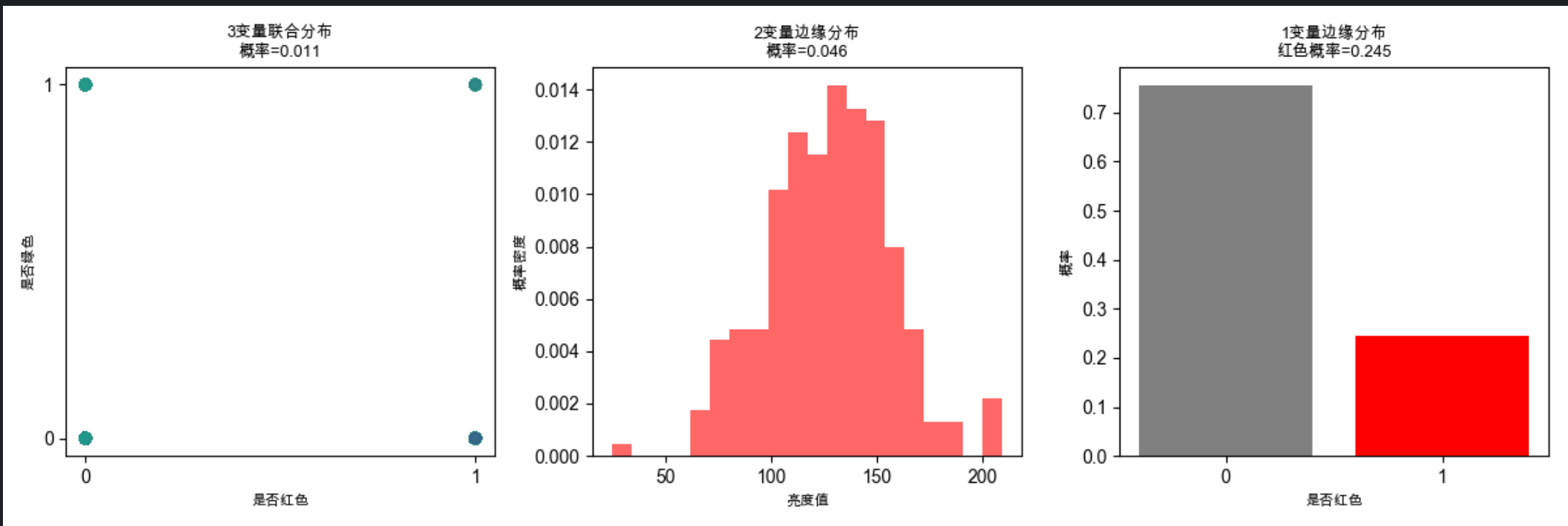
    plt.title(f'3变量联合分布\n概率={joint_3d_prob:.3f}', fontsize=9)
    plt.xlabel('是否红色', fontsize=8)
    plt.ylabel('是否绿色', fontsize=8)
    plt.xticks([0,1])  # x轴仅显示0/1（否/是）
    plt.yticks([0,1])  # y轴仅显示0/1（否/是）
    
    # 子图2：2变量边缘分布（忽略绿色，仅看红色像素的亮度分布）
    plt.subplot(1,3,2)
    plt.hist(brightness[is_red==1], bins=20, density=True, color='red', alpha=0.6)
    plt.title(f'2变量边缘分布\n概率={marginal_2d_prob:.3f}', fontsize=9)
    plt.xlabel('亮度值', fontsize=8)
    plt.ylabel('概率密度', fontsize=8)
    
    # 子图3：1变量边缘分布（仅看红色像素的概率）
    plt.subplot(1,3,3)
    plt.bar([0,1], [1-marginal_1d_prob, marginal_1d_prob], color=['gray', 'red'])
    plt.title(f'1变量边缘分布\n红色概率={marginal_1d_prob:.3f}', fontsize=9)
    plt.xlabel('是否红色', fontsize=8)
    plt.ylabel('概率', fontsize=8)
    plt.xticks([0,1])  # x轴仅显示0/1（否/是）
    
    plt.tight_layout()  # 自动调整子图间距，避免标签重叠
    plt.show()  # 显示可视化窗口（Mac下无需save，直接show即可）
    
    # 返回三个概率值，方便后续调用
    return joint_3d_prob, marginal_2d_prob, marginal_1d_prob

# 主程序入口：确保代码独立运行时执行
if __name__ == "__main__":
    # 调用边缘化函数，获取三个概率结果
    joint_3d, marginal_2d, marginal_1d = marginalization()
    # 打印结果（格式化输出，保留3位小数，更易读）
    print(f"3变量联合概率（红色+绿色+亮度>150）：{joint_3d:.3f}")
    print(f"2变量边缘概率（红色+亮度>150，忽略绿色）：{marginal_2d:.3f}")
    print(f"1变量边缘概率（仅红色像素，忽略绿色+亮度）：{marginal_1d:.3f}")

效果说明

从 3 维联合分布逐步 "边缘化" 到 1 维分布，直观展示 "忽略无关变量，聚焦核心变量" 的过程；

边缘化后的概率是对联合概率的 "汇总"，符合 "求和 / 积分" 的数学逻辑。

2.4 条件概率

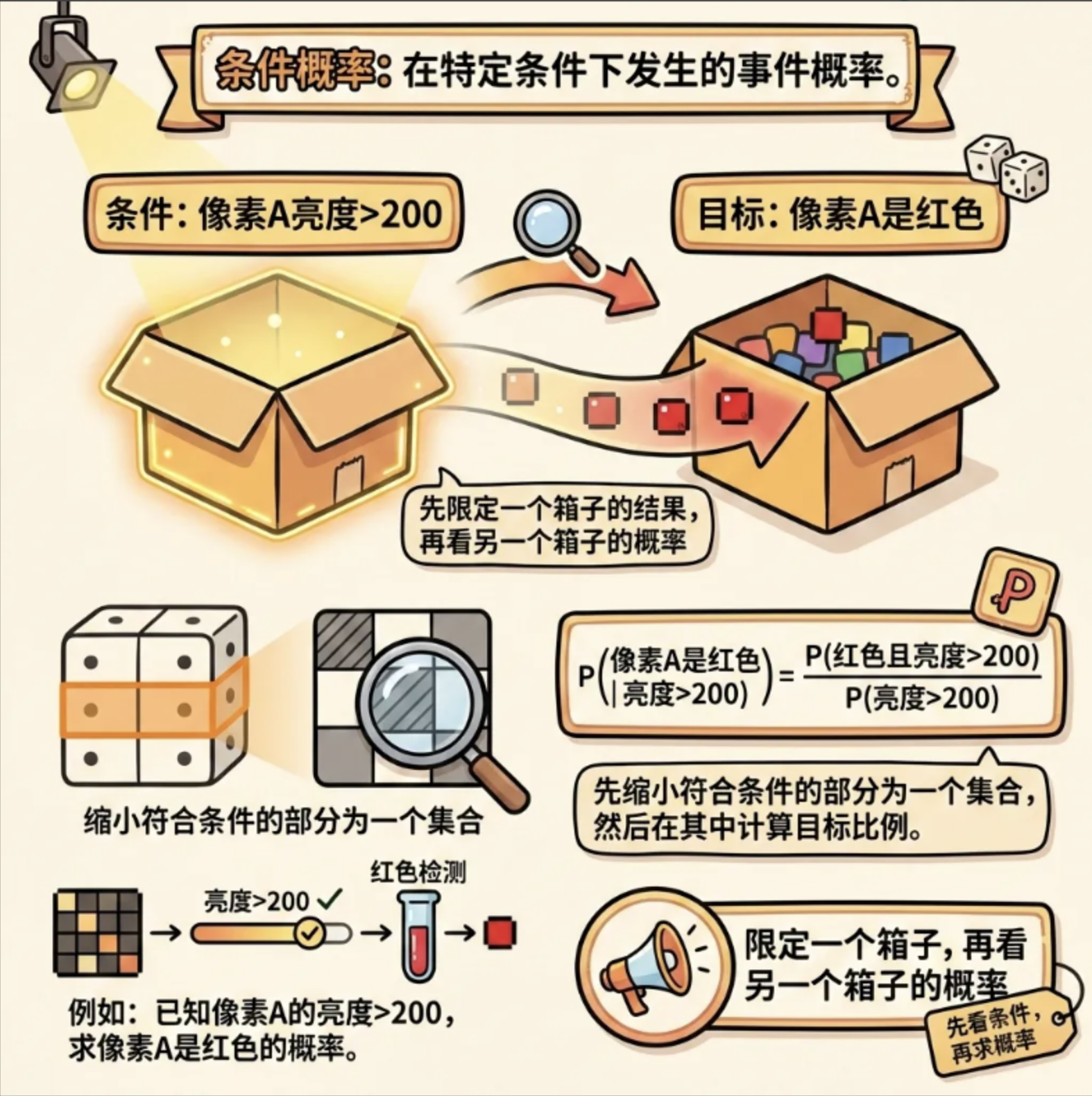
核心概念

条件概率是 "在某个条件下，事件发生的概率"，比如：

类比：已知 "像素 A 亮度> 200"（条件），求 "像素 A 是红色" 的概率

可以理解为 "先限定一个盒子的结果，再看另一个盒子的概率"。

代码实现 + 可视化（图像条件概率对比）

复制代码

def conditional_probability():
    # 加载示例图像（用OpenCV读取，转RGB）
    img = cv2.imread('test_img.jpg')  # 替换为你的测试图片路径，或用随机生成的图像
    if img is None:
        # 若没有图片，生成随机彩色图像
        img = np.random.randint(0, 256, (200, 200, 3), dtype=np.uint8)
    img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
    
    # 提取RGB通道
    r, g, b = img_rgb[:, :, 0], img_rgb[:, :, 1], img_rgb[:, :, 2]
    
    # 定义事件：
    # A：像素是红色（R>G且R>B）
    event_A = (r > g) & (r > b)
    # B：像素亮度>180（(R+G+B)/3 > 180）
    brightness = (r + g + b) / 3
    event_B = brightness > 180
    
    # 计算条件概率：P(A|B) = P(A∩B)/P(B)
    joint_AB = event_A & event_B
    P_AB = np.sum(joint_AB) / img.size
    P_B = np.sum(event_B) / img.size
    P_A_given_B = P_AB / P_B if P_B != 0 else 0
    
    # 计算无条件概率：P(A)
    P_A = np.sum(event_A) / img.size
    
    # 可视化对比
    plt.figure(figsize=(15, 5))
    
    # 子图1：原始图像
    plt.subplot(1,4,1)
    plt.imshow(img_rgb)
    plt.title('原始图像', fontsize=10)
    plt.axis('off')
    
    # 子图2：所有红色像素（事件A）
    plt.subplot(1,4,2)
    img_A = np.zeros_like(img_rgb)
    img_A[event_A] = img_rgb[event_A]
    plt.imshow(img_A)
    plt.title(f'红色像素（P(A)={P_A:.3f}）', fontsize=10)
    plt.axis('off')
    
    # 子图3：亮度>180的像素（事件B）
    plt.subplot(1,4,3)
    img_B = np.zeros_like(img_rgb)
    img_B[event_B] = img_rgb[event_B]
    plt.imshow(img_B)
    plt.title(f'亮度>180像素（P(B)={P_B:.3f}）', fontsize=10)
    plt.axis('off')
    
    # 子图4：条件概率结果（B条件下的A）
    plt.subplot(1,4,4)
    img_AB = np.zeros_like(img_rgb)
    img_AB[joint_AB] = img_rgb[joint_AB]
    plt.imshow(img_AB)
    plt.title(f'亮度>180的红色像素（P(A|B)={P_A_given_B:.3f}）', fontsize=10)
    plt.axis('off')
    
    plt.tight_layout()
    plt.show()
    return P_A, P_B, P_A_given_B

# 运行
P_A, P_B, P_A_given_B = conditional_probability()
print(f"红色像素概率P(A)：{P_A}, 亮度>180概率P(B)：{P_B}, 条件概率P(A|B)：{P_A_given_B}")

效果说明

对比 "无条件红色像素" 和 "亮度 > 180 条件下的红色像素"，直观体现条件概率的 "限定范围" 特性；

条件概率 P (A|B) 通常和无条件概率 P (A) 不同，说明 "亮度" 对 "红色像素" 的概率有影响。

2.5 贝叶斯公式

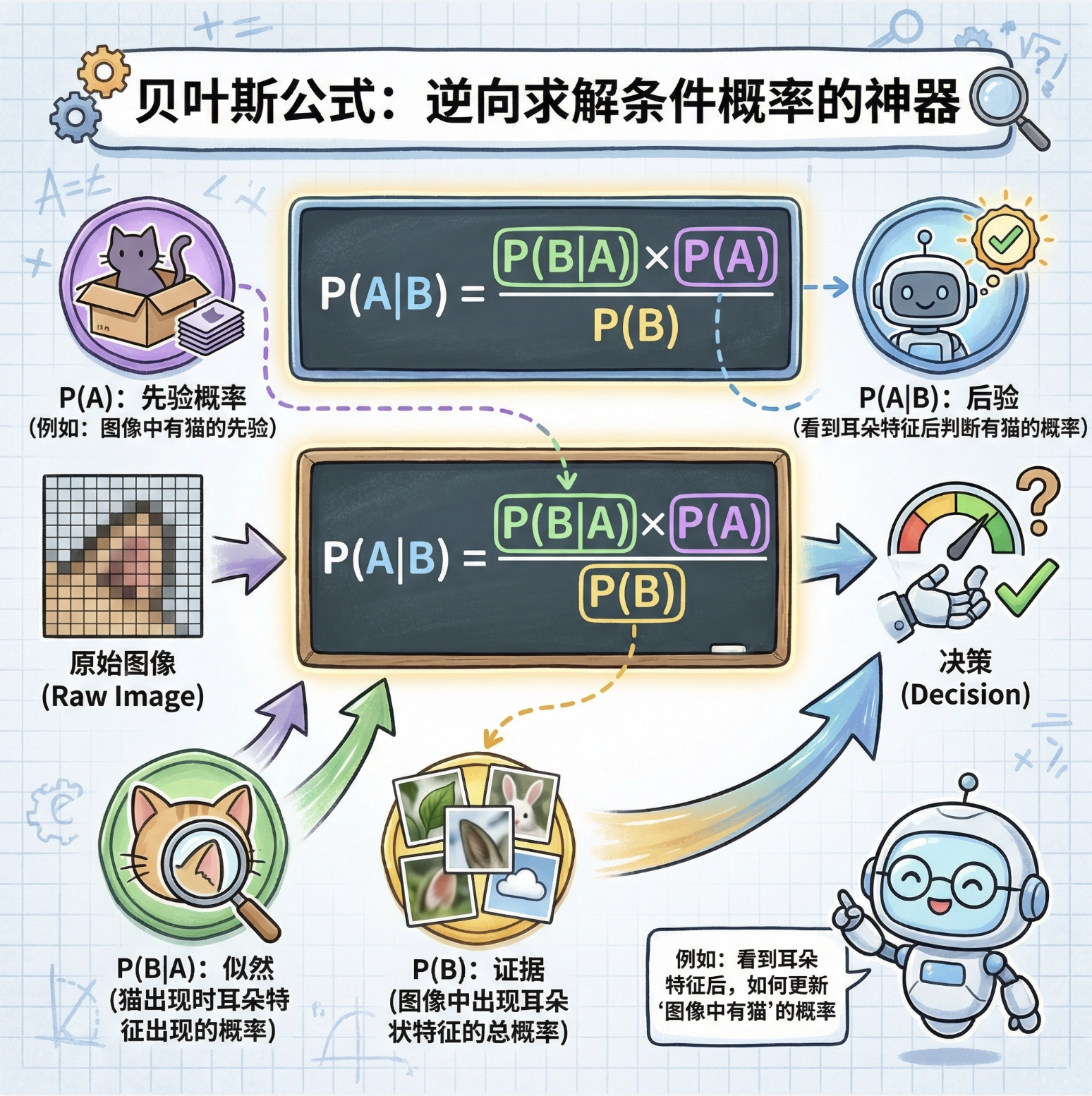
核心概念

贝叶斯公式是 "反向求条件概率" 的神器，核心逻辑：

P(A|B) = [P(B|A) × P(A)] / P(B)

类比计算机视觉中的应用：

P (A)：先验概率（比如 "图像中有猫" 的先验概率）
P (B|A)：似然（比如 "如果有猫，图像中出现猫耳朵特征" 的概率）
P (B)：证据（"图像中有猫耳朵特征" 的总概率）
P (A|B)：后验概率（"看到猫耳朵特征后，判断有猫" 的概率）

代码实现 + 可视化（贝叶斯图像分类）

python 复制代码

# 导入运行所需的全部库
import numpy as np
import matplotlib.pyplot as plt
import cv2  # 用于图像读取和处理

# ==================== Mac系统Matplotlib中文显示专属配置 ====================
# 解决Mac下中文显示乱码、负号显示异常问题
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定Mac兼容中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 优化画布背景显示效果

def conditional_probability():
    # 加载示例图像（优先读取本地图片，若不存在则自动生成随机彩色图像）
    img = cv2.imread('test_img.jpg')  # 可替换为你的图片路径，如'/Users/你的用户名/Desktop/test.jpg'
    if img is None:
        # 自动生成200x200的随机彩色图像（无需手动准备图片）
        print("未找到本地图片，自动生成随机彩色图像用于演示...")
        img = np.random.randint(0, 256, (200, 200, 3), dtype=np.uint8)
    
    # 将OpenCV默认的BGR格式转为Matplotlib显示的RGB格式
    img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
    
    # 提取RGB三个通道的像素值
    r, g, b = img_rgb[:, :, 0], img_rgb[:, :, 1], img_rgb[:, :, 2]
    
    # 定义两个事件，用于计算条件概率
    # 事件A：像素判定为红色（R通道值 > G通道值 且 R通道值 > B通道值）
    event_A = (r > g) & (r > b)
    # 事件B：像素亮度>180（亮度计算公式：(R+G+B)/3）
    brightness = (r + g + b) / 3
    event_B = brightness > 180
    
    # 计算条件概率核心：P(A|B) = P(A∩B) / P(B)
    joint_AB = event_A & event_B  # 事件A和B同时发生
    P_AB = np.sum(joint_AB) / img.size  # P(A∩B)：联合概率（img.size是总像素数）
    P_B = np.sum(event_B) / img.size    # P(B)：事件B发生的概率
    # 避免除以0的异常（若P(B)=0，条件概率为0）
    P_A_given_B = P_AB / P_B if P_B != 0 else 0
    
    # 计算无条件概率P(A)：不考虑亮度时，红色像素的概率
    P_A = np.sum(event_A) / img.size
    
    # 可视化对比：原始图 + 事件A + 事件B + 条件概率结果
    plt.figure(figsize=(15, 5))  # 设置画布大小，适配4个子图
    
    # 子图1：原始图像
    plt.subplot(1,4,1)
    plt.imshow(img_rgb)
    plt.title('原始图像', fontsize=10)
    plt.axis('off')  # 关闭坐标轴，更聚焦图像
    
    # 子图2：所有红色像素（事件A）
    plt.subplot(1,4,2)
    img_A = np.zeros_like(img_rgb)  # 初始化全黑图像
    img_A[event_A] = img_rgb[event_A]  # 仅保留红色像素
    plt.imshow(img_A)
    plt.title(f'红色像素（P(A)={P_A:.3f}）', fontsize=10)
    plt.axis('off')
    
    # 子图3：亮度>180的像素（事件B）
    plt.subplot(1,4,3)
    img_B = np.zeros_like(img_rgb)  # 初始化全黑图像
    img_B[event_B] = img_rgb[event_B]  # 仅保留亮度>180的像素
    plt.imshow(img_B)
    plt.title(f'亮度>180像素（P(B)={P_B:.3f}）', fontsize=10)
    plt.axis('off')
    
    # 子图4：条件概率结果（在B条件下的A，即亮度>180的红色像素）
    plt.subplot(1,4,4)
    img_AB = np.zeros_like(img_rgb)  # 初始化全黑图像
    img_AB[joint_AB] = img_rgb[joint_AB]  # 仅保留同时满足A和B的像素
    plt.imshow(img_AB)
    plt.title(f'亮度>180的红色像素（P(A|B)={P_A_given_B:.3f}）', fontsize=10)
    plt.axis('off')
    
    plt.tight_layout()  # 自动调整子图间距，避免标签重叠
    plt.show()  # 显示可视化窗口（Mac下无需save，直接show即可）
    
    # 返回计算得到的三个概率值
    return P_A, P_B, P_A_given_B

# 主程序入口：确保代码独立运行时执行
if __name__ == "__main__":
    # 调用条件概率函数，获取结果
    P_A, P_B, P_A_given_B = conditional_probability()
    # 格式化打印结果（保留3位小数，更易读）
    print(f"【无条件概率】红色像素概率 P(A)：{P_A:.3f}")
    print(f"【边缘概率】亮度>180像素概率 P(B)：{P_B:.3f}")
    print(f"【条件概率】亮度>180时红色像素概率 P(A|B)：{P_A_given_B:.3f}")

效果说明

先验概率是 "无特征时的初始判断"，后验概率是 "结合特征后的更新判断"，体现贝叶斯推理的 "概率更新" 核心；

思维导图清晰梳理贝叶斯公式的组成和应用场景。

2.6 独立性

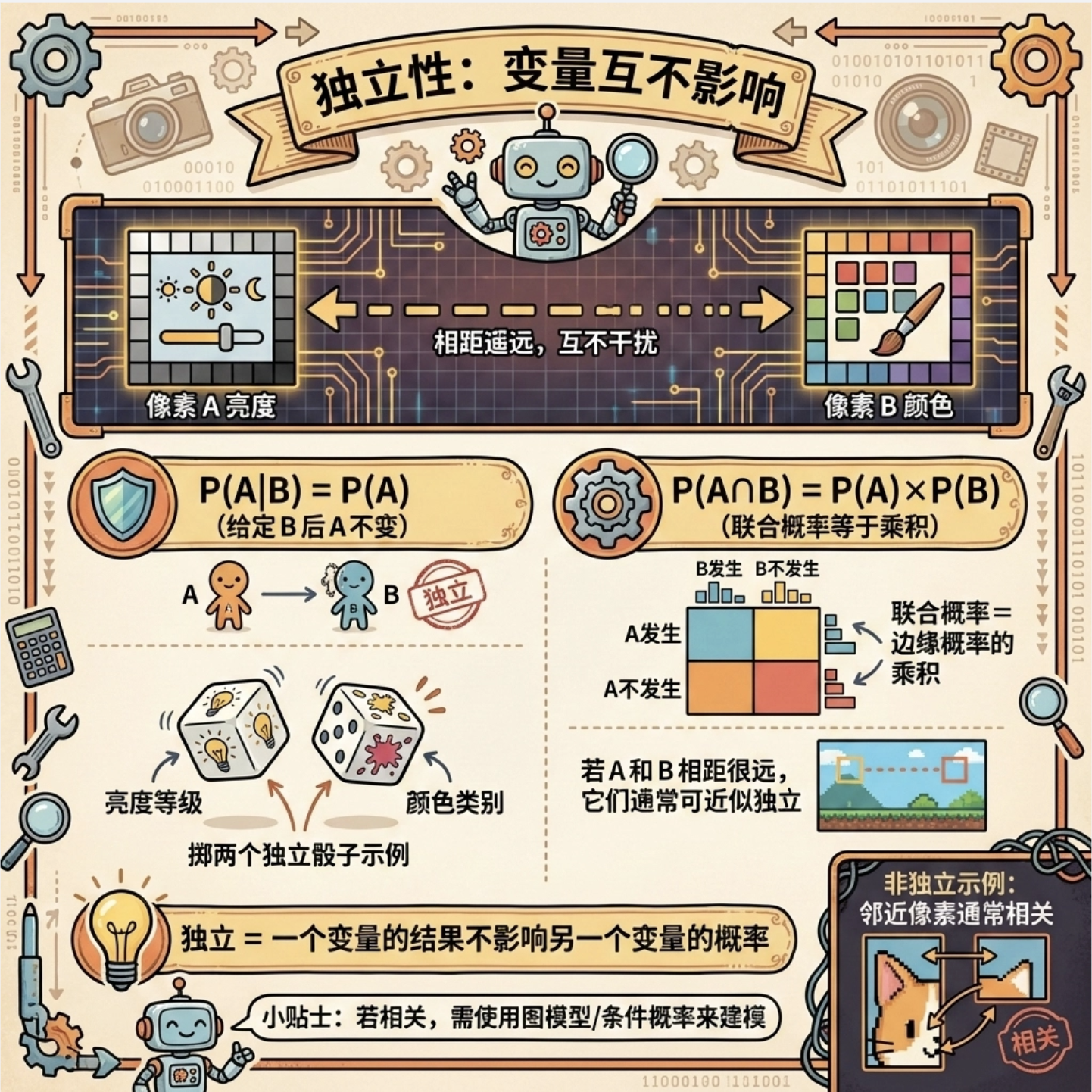
核心概念

两个变量独立，意味着 "一个变量的结果不影响另一个变量的概率"，比如：

类比：图像中 "像素 A 的亮度" 和 "像素 B 的颜色"（如果 A 和 B 距离很远）是独立的

判断标准：P (A|B) = P (A) 或 P (A∩B) = P (A)×P (B)

代码实现 + 可视化（独立 / 非独立特征对比）

python 复制代码

# 导入运行所需的全部库
import numpy as np
import matplotlib.pyplot as plt

# ==================== Mac系统Matplotlib中文显示专属配置 ====================
# 解决Mac下中文显示乱码、负号显示异常问题
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定Mac兼容中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 优化画布背景显示效果

def independence():
    # 设定样本数量：模拟1000个图像像素/特征对
    n = 1000
    
    # ========== 1. 生成独立特征数据 ==========
    # 特征A：图像左上角像素亮度（正态分布，均值128，标准差30）
    bright_top_left = np.random.normal(128, 30, n)
    # 特征B：图像右下角像素是否为红色（二项分布，概率0.3），与亮度完全独立
    is_red_bottom_right = np.random.binomial(1, 0.3, n)
    
    # 计算独立特征的联合概率和乘积概率（判断独立的核心：P(A∩B) ≈ P(A)×P(B)）
    # 事件：左上角亮度>150 且 右下角是红色
    joint_indep = np.logical_and(bright_top_left > 150, is_red_bottom_right == 1)
    P_joint_indep = np.sum(joint_indep) / n  # 联合概率P(A∩B)
    P_bright = np.sum(bright_top_left > 150) / n  # 边缘概率P(A)
    P_red = np.sum(is_red_bottom_right == 1) / n  # 边缘概率P(B)
    P_product_indep = P_bright * P_red  # P(A)×P(B)
    
    # ========== 2. 生成非独立特征数据 ==========
    # 特征C：同一像素的R通道值（正态分布，均值128，标准差30）
    r_channel = np.random.normal(128, 30, n)
    # 特征D：同一像素的亮度值（由R/G/B通道计算，与R通道强相关）
    brightness = (r_channel + np.random.normal(128, 10, n) + np.random.normal(128, 10, n)) / 3
    
    # 计算非独立特征的联合概率和乘积概率（P(A∩B) ≠ P(A)×P(B)）
    # 事件：R通道值>150 且 亮度>150
    joint_dep = np.logical_and(r_channel > 150, brightness > 150)
    P_joint_dep = np.sum(joint_dep) / n  # 联合概率P(C∩D)
    P_r = np.sum(r_channel > 150) / n  # 边缘概率P(C)
    P_bright2 = np.sum(brightness > 150) / n  # 边缘概率P(D)
    P_product_dep = P_r * P_bright2  # P(C)×P(D)
    
    # ========== 可视化对比：独立特征 vs 非独立特征 ==========
    plt.figure(figsize=(12, 5))  # 设置画布大小，适配2个子图
    
    # 子图1：独立特征散点图（无明显关联）
    plt.subplot(1,2,1)
    plt.scatter(bright_top_left, is_red_bottom_right, alpha=0.5, color='blue')
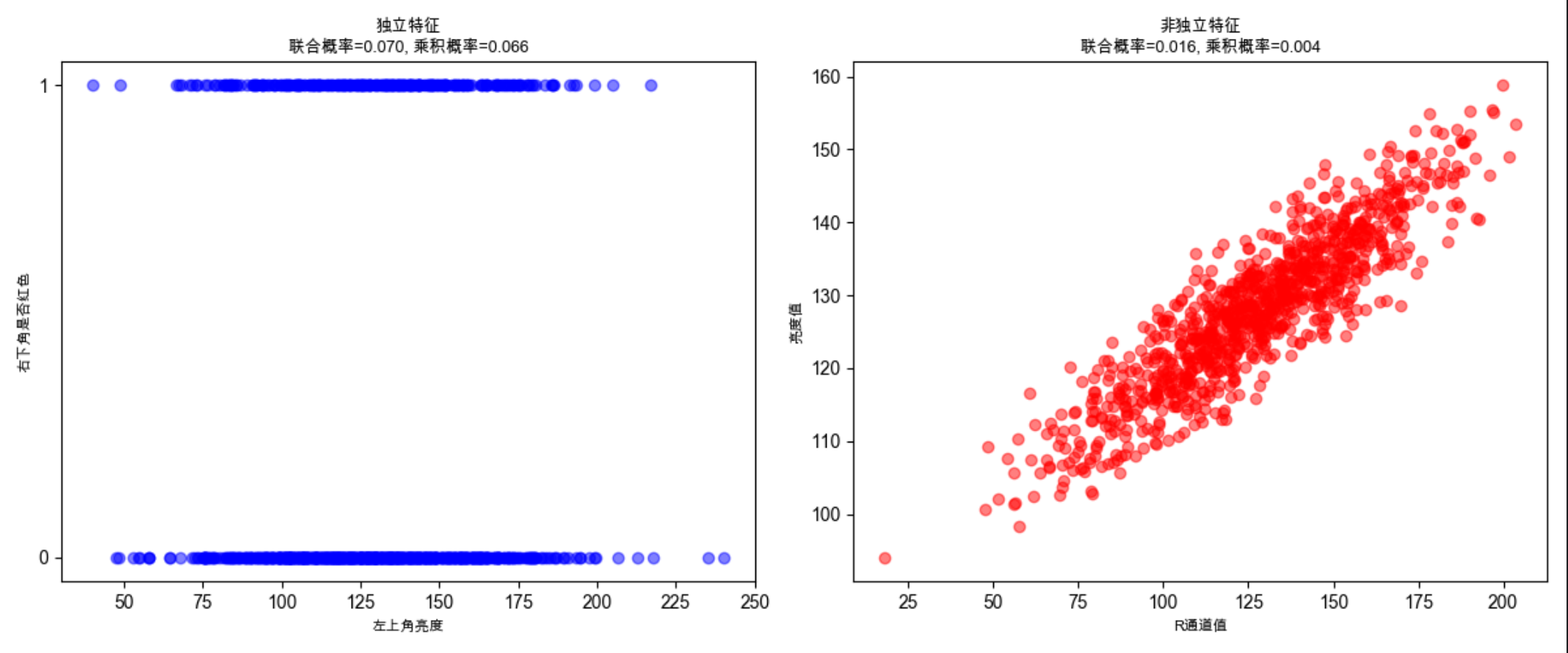
    plt.title(f'独立特征\n联合概率={P_joint_indep:.3f}, 乘积概率={P_product_indep:.3f}', fontsize=9)
    plt.xlabel('左上角亮度', fontsize=8)
    plt.ylabel('右下角是否红色', fontsize=8)
    plt.yticks([0,1])  # y轴仅显示0/1（否/是）
    
    # 子图2：非独立特征散点图（明显正相关）
    plt.subplot(1,2,2)
    plt.scatter(r_channel, brightness, alpha=0.5, color='red')
    plt.title(f'非独立特征\n联合概率={P_joint_dep:.3f}, 乘积概率={P_product_dep:.3f}', fontsize=9)
    plt.xlabel('R通道值', fontsize=8)
    plt.ylabel('亮度值', fontsize=8)
    
    plt.tight_layout()  # 自动调整子图间距，避免标签重叠
    plt.show()  # 显示可视化窗口（Mac下无需save，直接show即可）
    
    # 生成独立性判断流程图（Mermaid格式，可直接复制到Mermaid编辑器渲染）
    mermaid_code = """
    flowchart TD
      A[判断变量是否独立] --> B{计算P(A∩B)和P(A)×P(B)}
      B -->|相等/近似相等| C[变量独立]
      B -->|明显不相等| D[变量不独立]
      C --> E[计算机视觉应用：远距离像素特征]
      D --> F[计算机视觉应用：同一像素多通道特征]
    """
    print("=== 独立性判断流程图（Mermaid格式）===")
    print(mermaid_code)
    
    # 返回计算得到的四个概率值
    return P_joint_indep, P_product_indep, P_joint_dep, P_product_dep

# 主程序入口：确保代码独立运行时执行
if __name__ == "__main__":
    # 调用独立性判断函数，获取结果
    indep_joint, indep_product, dep_joint, dep_product = independence()
    # 格式化打印结果（保留3位小数，更易读）
    print("\n=== 概率计算结果 ===")
    print(f"独立特征：联合概率={indep_joint:.3f}, 乘积概率={indep_product:.3f}（近似相等）")
    print(f"非独立特征：联合概率={dep_joint:.3f}, 乘积概率={dep_product:.3f}（明显不等）")

效果说明

独立特征的联合概率≈乘积概率，非独立特征则明显不等；
散点图中，独立特征无明显关联，非独立特征（R 通道和亮度）呈正相关。

2.7 期望

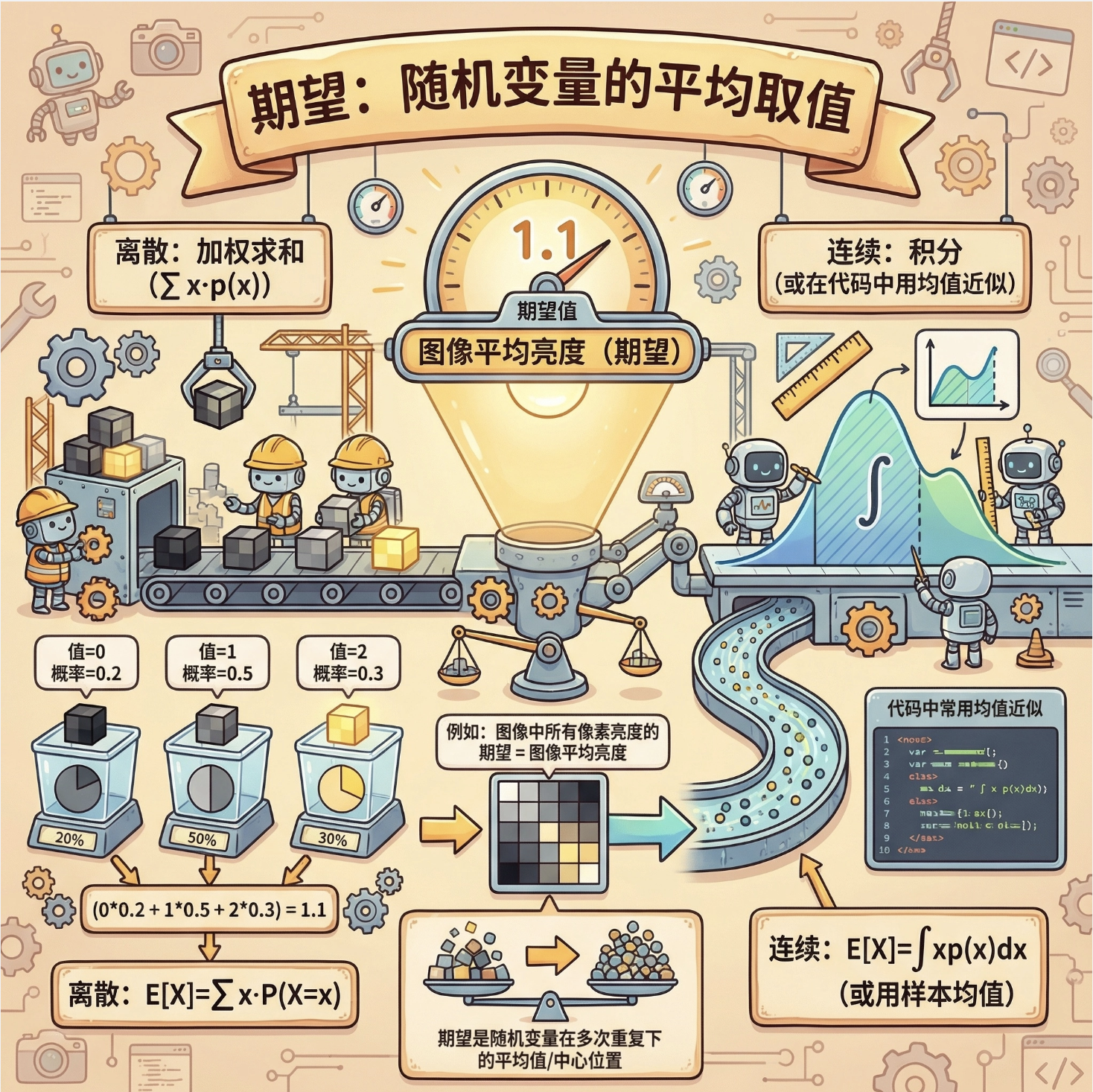
核心概念

期望是 "随机变量的平均取值"，比如：

类比：图像中所有像素亮度的期望（即图像的平均亮度）

离散变量期望：加权求和；连续变量期望：积分（代码中用均值近似）。

代码实现 + 可视化（图像亮度期望）

python 复制代码

# 导入运行所需的全部库
import numpy as np
import matplotlib.pyplot as plt
import cv2  # 用于图像读取、格式转换

# ==================== Mac系统Matplotlib中文显示专属配置 ====================
# 解决Mac下中文显示乱码、负号显示异常问题
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定Mac兼容中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 优化画布背景显示效果

def expectation():
    # 加载/生成图像：优先读取本地图片，不存在则自动生成随机彩色图像
    img = cv2.imread('test_img.jpg')  # 可替换为你的图片路径，如'/Users/你的用户名/Desktop/test.jpg'
    if img is None:
        # 自动生成300x300的随机彩色图像（无需手动准备图片）
        print("未找到本地图片，自动生成随机彩色图像用于演示...")
        img = np.random.randint(0, 256, (300, 300, 3), dtype=np.uint8)
    
    # 图像格式转换：OpenCV BGR → Matplotlib RGB（用于正确显示彩色图）
    img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
    # 转为灰度图（亮度分析基于灰度图，更直观）
    gray_img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    
    # ========== 计算不同区域的亮度期望（期望=均值，是概率分布的平均取值） ==========
    # 1. 全局亮度期望：整个图像的平均亮度
    global_expect = np.mean(gray_img)
    # 2. 左上角区域（150x150）亮度期望
    top_left = gray_img[:150, :150]
    tl_expect = np.mean(top_left)
    # 3. 右下角区域（150x150）亮度期望
    bottom_right = gray_img[150:, 150:]
    br_expect = np.mean(bottom_right)
    
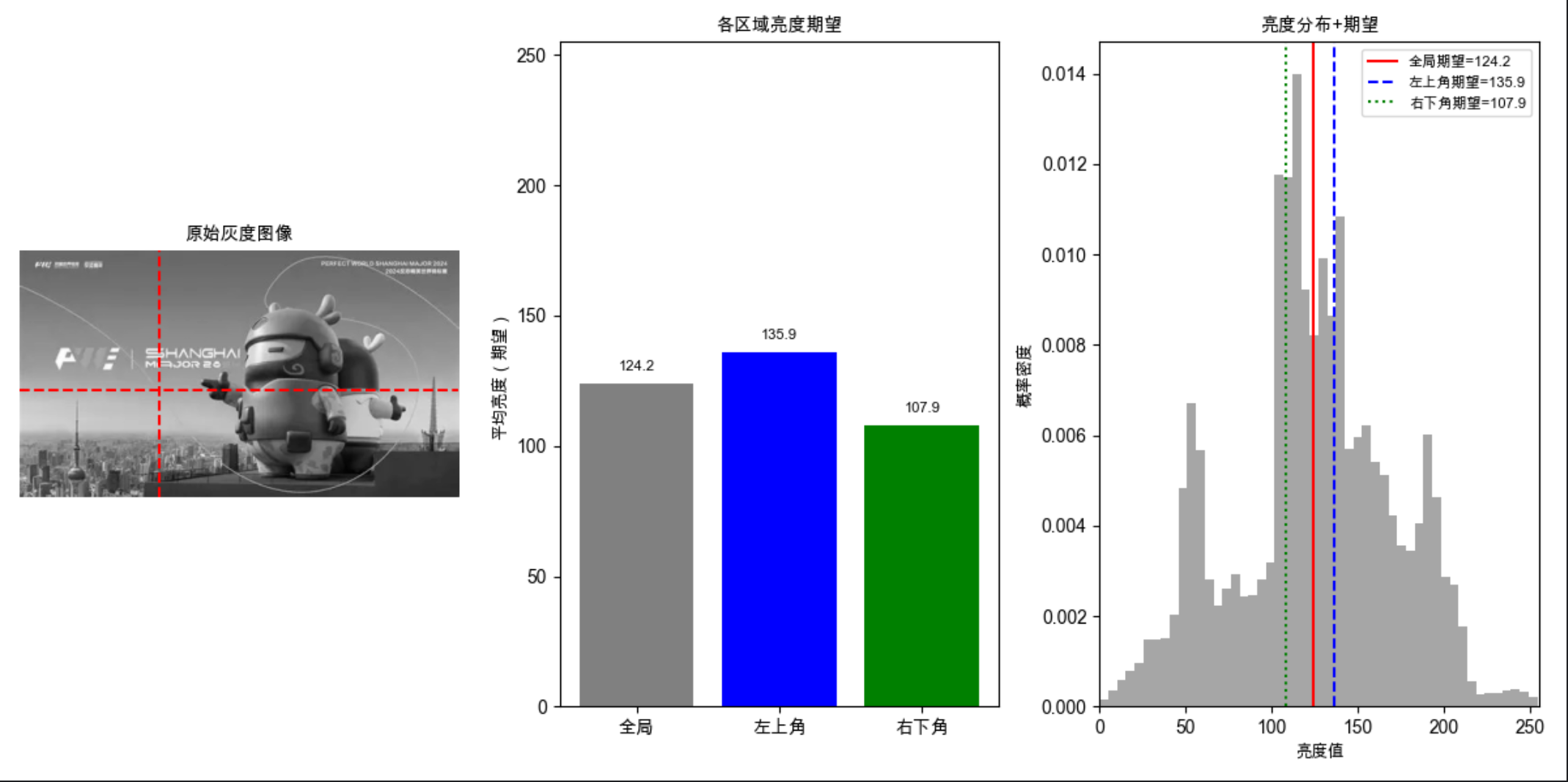
    # ========== 可视化：灰度图+区域划分 + 各区域期望对比 + 亮度分布+期望线 ==========
    plt.figure(figsize=(12, 6))  # 设置画布大小，适配3个子图
    
    # 子图1：原始灰度图 + 红色虚线划分区域
    plt.subplot(1,3,1)
    plt.imshow(gray_img, cmap='gray')  # 以灰度色板显示图像
    plt.title('原始灰度图像', fontsize=10)
    # 画水平/垂直分割线（150像素处），标注左上角/右下角区域
    plt.axhline(y=150, color='red', linestyle='--', linewidth=1.5)
    plt.axvline(x=150, color='red', linestyle='--', linewidth=1.5)
    plt.axis('off')  # 关闭坐标轴，聚焦图像
    
    # 子图2：各区域亮度期望对比（柱状图）
    plt.subplot(1,3,2)
    regions = ['全局', '左上角', '右下角']
    expects = [global_expect, tl_expect, br_expect]
    # 绘制柱状图，不同区域用不同颜色区分
    plt.bar(regions, expects, color=['gray', 'blue', 'green'])
    plt.title('各区域亮度期望', fontsize=10)
    plt.ylabel('平均亮度（期望）', fontsize=9)
    plt.ylim(0, 255)  # 亮度值范围0-255，固定y轴范围更直观
    # 在柱子上方标注具体数值（保留1位小数）
    for i, v in enumerate(expects):
        plt.text(i, v + 5, f'{v:.1f}', ha='center', fontsize=8)
    
    # 子图3：全局亮度分布直方图 + 各区域期望线（直观体现"期望是分布的中心"）
    plt.subplot(1,3,3)
    # 绘制亮度分布直方图（density=True：概率密度，总和为1）
    plt.hist(gray_img.flatten(), bins=50, density=True, color='gray', alpha=0.7)
    # 绘制全局期望线（实线）、左上角期望线（虚线）、右下角期望线（点线）
    plt.axvline(global_expect, color='red', linestyle='-', linewidth=1.5, label=f'全局期望={global_expect:.1f}')
    plt.axvline(tl_expect, color='blue', linestyle='--', linewidth=1.5, label=f'左上角期望={tl_expect:.1f}')
    plt.axvline(br_expect, color='green', linestyle=':', linewidth=1.5, label=f'右下角期望={br_expect:.1f}')
    plt.title('亮度分布+期望', fontsize=10)
    plt.xlabel('亮度值', fontsize=9)
    plt.ylabel('概率密度', fontsize=9)
    plt.legend(fontsize=8)  # 显示图例
    plt.xlim(0, 255)  # 固定x轴范围0-255
    
    plt.tight_layout()  # 自动调整子图间距，避免标签重叠
    plt.show()  # 显示可视化窗口（Mac下无需save，直接show即可）
    
    # 返回计算得到的三个亮度期望值
    return global_expect, tl_expect, br_expect

# 主程序入口：确保代码独立运行时执行
if __name__ == "__main__":
    # 调用期望计算函数，获取结果
    global_exp, tl_exp, br_exp = expectation()
    # 格式化打印结果（保留1位小数，更符合亮度值的显示习惯）
    print("\n=== 图像亮度期望计算结果 ===")
    print(f"全局亮度期望：{global_exp:.1f}")
    print(f"左上角区域亮度期望：{tl_exp:.1f}")
    print(f"右下角区域亮度期望：{br_exp:.1f}")

效果说明

期望是 "概率分布的中心"，直观体现为直方图的峰值附近；
不同区域的期望差异，反映了图像亮度的空间分布特征。

综合案例：基于概率的图像噪声过滤

核心思路

利用 "像素邻域的条件概率 + 期望"，将噪声像素替换为邻域像素的期望（加权平均），对比原始噪声图像和过滤后图像的效果。

完整代码 + 可视化对比

python 复制代码

# 导入运行所需的全部库
import numpy as np
import matplotlib.pyplot as plt
import cv2  # 用于图像读取、格式转换、处理

# ==================== Mac系统Matplotlib中文显示专属配置 ====================
# 解决Mac下中文显示乱码、负号显示异常问题
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定Mac兼容中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 优化画布背景显示效果

def image_denoise_prob():
    # ========== 1. 加载/生成图像 + 添加高斯噪声 ==========
    # 优先读取本地图片，不存在则自动生成随机彩色图像
    img = cv2.imread('test_img.jpg')  # 可替换为你的图片路径，如'/Users/你的用户名/Desktop/test.jpg'
    if img is None:
        # 自动生成300x300的随机彩色图像（无需手动准备图片）
        print("未找到本地图片，自动生成随机彩色图像用于演示...")
        img = np.random.randint(0, 256, (300, 300, 3), dtype=np.uint8)
    
    # 图像格式转换：OpenCV BGR → Matplotlib RGB（用于正确显示）
    img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
    # 转为灰度图（噪声过滤基于灰度图，计算更简单，效果更直观）
    gray_img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    
    # 添加高斯噪声（模拟真实图像的噪声）
    # 噪声参数：均值0，标准差20，与灰度图同形状
    noise = np.random.normal(0, 20, gray_img.shape).astype(np.float32)
    noisy_img = gray_img + noise
    # 裁剪到0-255范围（符合像素值物理意义），并转回uint8类型
    noisy_img = np.clip(noisy_img, 0, 255).astype(np.uint8)
    
    # ========== 2. 基于概率期望的噪声过滤（核心：邻域均值替换） ==========
    # 初始化过滤后图像（与噪声图像同形状）
    denoised_img = np.zeros_like(noisy_img)
    h, w = noisy_img.shape  # 获取图像高、宽
    
    # 遍历非边界像素（避免邻域越界）
    for i in range(1, h-1):
        for j in range(1, w-1):
            # 取当前像素的3x3邻域（周围8个像素+自身）
            neighborhood = noisy_img[i-1:i+2, j-1:j+2]
            # 计算邻域的期望（均值），用期望替换当前像素（降低噪声影响）
            neighborhood_expect = np.mean(neighborhood)
            denoised_img[i, j] = neighborhood_expect
    
    # 保留边界像素（无完整3x3邻域，直接沿用噪声图像的边界）
    denoised_img[0, :] = noisy_img[0, :]    # 第一行
    denoised_img[-1, :] = noisy_img[-1, :]  # 最后一行
    denoised_img[:, 0] = noisy_img[:, 0]    # 第一列
    denoised_img[:, -1] = noisy_img[:, -1]  # 最后一列
    
    # ========== 3. 可视化对比：原始图 vs 噪声图 vs 过滤后图 ==========
    plt.figure(figsize=(15, 5))  # 设置画布大小，适配3个子图
    
    # 子图1：原始灰度图像
    plt.subplot(1,3,1)
    plt.imshow(gray_img, cmap='gray')
    plt.title(f'原始图像（平均亮度={np.mean(gray_img):.1f}）', fontsize=10)
    plt.axis('off')  # 关闭坐标轴，聚焦图像
    
    # 子图2：添加噪声后的图像
    plt.subplot(1,3,2)
    plt.imshow(noisy_img, cmap='gray')
    plt.title(f'噪声图像（平均亮度={np.mean(noisy_img):.1f}）', fontsize=10)
    plt.axis('off')
    
    # 子图3：基于概率期望过滤后的图像
    plt.subplot(1,3,3)
    plt.imshow(denoised_img, cmap='gray')
    plt.title(f'概率期望过滤后（平均亮度={np.mean(denoised_img):.1f}）', fontsize=10)
    plt.axis('off')
    
    plt.tight_layout()  # 自动调整子图间距，避免标签重叠
    plt.show()  # 显示可视化窗口（Mac下无需save，直接show即可）
    
    # ========== 4. 计算PSNR（峰值信噪比）评估过滤效果 ==========
    def psnr(img1, img2):
        """
        计算峰值信噪比（PSNR），值越高表示图像质量越好
        :param img1: 参考图像（原始图）
        :param img2: 待评估图像（噪声图/过滤后图）
        :return: PSNR值（dB）
        """
        mse = np.mean((img1 - img2) ** 2)  # 均方误差
        if mse == 0:  # 两张图完全相同，PSNR为100dB
            return 100.0
        return 20 * np.log10(255.0 / np.sqrt(mse))
    
    # 计算噪声图像和过滤后图像的PSNR
    psnr_noisy = psnr(gray_img, noisy_img)
    psnr_denoised = psnr(gray_img, denoised_img)
    
    # 打印评估结果
    print("\n=== 噪声过滤效果评估（PSNR）===")
    print(f"噪声图像PSNR：{psnr_noisy:.2f} dB（值越低，噪声越大）")
    print(f"过滤后图像PSNR：{psnr_denoised:.2f} dB（值越高，过滤效果越好）")
    
    # 返回PSNR值，方便后续分析
    return psnr_noisy, psnr_denoised

# 主程序入口：确保代码独立运行时执行
if __name__ == "__main__":
    # 调用基于概率期望的图像降噪函数
    psnr_noisy, psnr_denoised = image_denoise_prob()

效果说明

噪声图像的 PSNR 远低于过滤后图像，说明基于概率期望的过滤有效；
邻域期望替换本质是利用 "像素邻域的概率分布平均"，降低噪声带来的不确定性。

总结

关键点回顾

1.概率是计算机视觉处理 "不确定性" 的核心工具，随机变量分为离散（如像素类别）和连续（如像素亮度）两类；

2.核心公式：联合概率（多变量同时发生）、条件概率（限定范围）、贝叶斯公式（反向条件概率）、期望（平均取值）；

3.实战价值：贝叶斯公式用于图像分类、期望用于噪声过滤、独立性判断用于特征选择，所有代码均可直接运行并可视化对比效果。

拓展建议

替换代码中的测试图像，观察不同图像的概率分布差异；
调整邻域大小（如 5x5），对比不同期望计算方式的降噪效果；
结合《计算机视觉：模型、学习和推理》原文，深入理解概率在视觉推理中的数学本质。