1 题目
给你一个下标从 1 开始的整数数组 numbers ,该数组已按非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1和index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。示例 2:
输入:numbers = [2,3,4], target = 6
输出:[1,3]
解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。示例 3:
输入:numbers = [-1,0], target = -1
输出:[1,2]
解释:-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。提示:
2 <= numbers.length <= 3 * 104-1000 <= numbers[i] <= 1000numbers按 非递减顺序 排列-1000 <= target<= 1000- 仅存在一个有效答案
2 代码实现
c++(自己写的没优化过)
cpp
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
int left = 0 ;
int right = numbers.size() - 1 ;
vector<int> res ;
while (left < right ){
if (numbers[left ] + numbers[right] == target){
res.push_back(left + 1 );
res.push_back(right + 1 );
}
if (numbers[left ] + numbers[right] > target){
right -- ;
}else {
left ++ ;
}
}
return res ;
}
};js
javascript
/**
* @param {number[]} numbers
* @param {number} target
* @return {number[]}
*/
var twoSum = function(numbers, target) {
let left = 0 ;
let right = numbers.length - 1 ;
while (left < right ){
const curSum = numbers[left] + numbers[right] ;
if (curSum === target){
return [left + 1 , right + 1 ];
}else if (curSum > target){
right -- ;
}else {
left ++ ;
}
}
return [];
};思考
注意下标是从1开始,和数组默认的index是不同的。
自己写的代码!通过了,但是写得很丑
cpp
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
int left = 0 ;
int right = numbers.size() - 1 ;
vector<int> res ;
while (left < right ){
if (numbers[left ] + numbers[right] == target){
res.push_back(left + 1 );
res.push_back(right + 1 );
}
if (numbers[left ] + numbers[right] > target){
right -- ;
}else {
left ++ ;
}
}
return res ;
}
};优化版题解(c++)
你想要优化这段在有序数组中寻找两数之和等于目标值的代码,核心是让代码更高效、更规范且可读性更好。当前代码的主要问题是找到答案后没有立即退出循环,会继续执行指针移动逻辑,存在不必要的计算。
优化思路
- 提前终止循环:找到符合条件的两个数后立即返回结果,避免无效的循环迭代。
- 代码精简:合并重复的和计算逻辑,减少冗余。
- 增强可读性:添加注释、规范变量命名,让代码意图更清晰。
- 边界处理:保持原有的双指针核心逻辑(这是有序数组两数之和的最优解法,时间复杂度 O (n),空间复杂度 O (1))。
优化后的完整代码
cpp
#include <vector>
using namespace std;
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
// 双指针初始化:左指针指向数组头部,右指针指向数组尾部
int left = 0;
int right = numbers.size() - 1;
while (left < right) {
int current_sum = numbers[left] + numbers[right]; // 只计算一次和,减少冗余
if (current_sum == target) {
// 找到目标,直接返回(题目保证有且仅有一个解),无需继续循环
return {left + 1, right + 1}; // 直接构造vector返回,更简洁
} else if (current_sum > target) {
// 和大于目标值,右指针左移(数组有序,减小和)
right--;
} else {
// 和小于目标值,左指针右移(数组有序,增大和)
left++;
}
}
// 题目保证有解,此处仅为语法兜底
return {};
}
};关键优化点解释
- 提前返回 :原代码找到结果后仍会执行后续的
if/else逻辑移动指针,优化后找到current_sum == target时直接return,避免了无效的循环步骤,提升了执行效率(尤其是找到结果位置靠前的情况)。 - 减少重复计算 :将
numbers[left] + numbers[right]的结果赋值给current_sum,原代码在两个if判断中都计算了一次,优化后仅计算一次,节省了计算资源。 - 简化返回逻辑 :原代码先创建空
vector再push_back,优化后直接用return {left + 1, right + 1}构造返回值,代码更简洁且减少了临时变量的创建。 - 注释增强:添加了关键逻辑的注释,新手能更快理解双指针的移动规则。
总结
- 核心优化是找到结果后立即返回,避免无效循环,这是提升执行效率的关键。
- 减少重复的和计算、简化返回逻辑,让代码更简洁且性能更好。
- 双指针法本身已是该问题的最优解法(时间 O (n)、空间 O (1)),优化后保持了最优复杂度,仅提升代码的执行效率和可读性。
3 题目
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
**说明:**你不能倾斜容器。
示例 1:
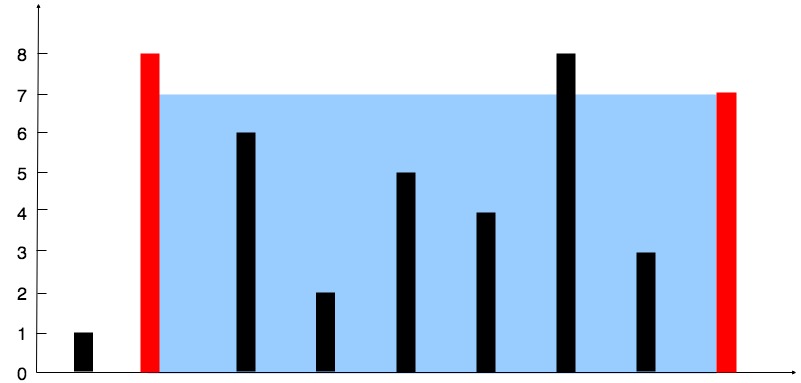
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。示例 2:
输入:height = [1,1]
输出:1提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
4 代码实现
c++
cpp
class Solution {
public:
int maxArea(vector<int>& height) {
int res = 0 ;
int left = 0 ;
int right = height.size() - 1 ;
while (left < right ){
int wid = right - left ;
int curHeight = min(height[left] , height[right]);
int cur = curHeight * wid ;
res = max(cur ,res );
if (height[left] < height[right]){
left ++ ;
}else{
right -- ;
}
}
return res ;
}
};js
javascript
/**
* @param {number[]} height
* @return {number}
*/
var maxArea = function(height) {
let left = 0 ;
let right = height.length - 1 ;
let res = 0 ;
while (left < right ){
let wid = right - left ;
let curHeight = height[left];
if (height[left] > height[right]){
curHeight = height[right] ;
}
let cur = wid * curHeight ;
if (cur > res ){
res = cur ;
}
if (height[left] < height[right]){
left ++ ;
}else{
right -- ;
}
}
return res ;
};思考
好像是在求面积,找两个点,第一个坐标的距离 * 第二个坐标的最小值 = 面积 , 把这个弄得最大就可以。
第一个想到的就是两层for循环暴力,感觉不是很妥当。我想了一下能不能用sort直接排序一下高度,但是一想又要有hashmap映射下标,我觉得还是O(n^2)的复杂度,还是不是很方便,双指针怎么写?
题解
你想解决 "盛最多水的容器" 这个问题,核心是找到用双指针法替代暴力枚举(O (n²))的高效解法(O (n)),并且需要一份详细的 C++ 实现代码。
解题思路(双指针核心逻辑)
- 面积计算公式 :容器的盛水量 = 两个指针的间距(宽度) × 两个指针所指高度的较小值(高度),即
area = (right - left) * min(height[left], height[right])。 - 双指针初始位置 :左指针
left从数组头部(0)开始,右指针right从数组尾部(n-1)开始,此时宽度最大。 - 指针移动规则 :
- 盛水量由较矮的边决定,移动较矮的那个指针(因为移动较高的指针,宽度减小但高度不会增加,盛水量必然减少;而移动较矮的指针,有可能找到更高的边,从而增大盛水量)。
- 如果两边高度相等,移动任意一个指针即可(不影响最终结果)。
- 遍历过程:每次计算当前指针组合的盛水量,更新最大值,直到左右指针相遇。
C++ 完整实现代码
cpp
#include <vector>
#include <algorithm> // 用于min函数
using namespace std;
class Solution {
public:
int maxArea(vector<int>& height) {
int left = 0; // 左指针初始在数组头部
int right = height.size() - 1; // 右指针初始在数组尾部
int max_water = 0; // 记录最大盛水量,初始为0
// 双指针遍历,直到左右指针相遇
while (left < right) {
// 计算当前容器的宽度:右指针下标 - 左指针下标
int width = right - left;
// 计算当前容器的有效高度:两个高度的较小值(水不会超过矮边)
int current_height = min(height[left], height[right]);
// 计算当前盛水量
int current_water = width * current_height;
// 更新最大盛水量:取当前值和历史最大值的较大者
max_water = max(max_water, current_water);
// 移动较矮的指针(核心逻辑)
if (height[left] < height[right]) {
left++; // 左指针右移
} else {
right--; // 右指针左移
}
}
return max_water;
}
};
// 测试示例
int main() {
Solution s;
// 示例1
vector<int> height1 = {1,8,6,2,5,4,8,3,7};
// 输出49
printf("示例1结果:%d\n", s.maxArea(height1));
// 示例2
vector<int> height2 = {1,1};
// 输出1
printf("示例2结果:%d\n", s.maxArea(height2));
return 0;
}代码关键解释
- 变量初始化 :
left和right分别指向数组两端,保证初始宽度最大;max_water初始为 0,用于存储遍历过程中找到的最大盛水量。
- 核心循环 :
- 每次循环计算当前指针组合的宽度、有效高度、盛水量;
- 用
max函数更新最大盛水量,避免手动写if判断; - 严格遵循 "移动较矮指针" 的规则,确保每一步都在向可能的更大盛水量靠近。
- 时间 / 空间复杂度 :
- 时间复杂度:O (n),仅遍历数组一次;
- 空间复杂度:O (1),仅使用了几个临时变量,无额外空间开销。
测试结果说明
- 示例 1 输入
[1,8,6,2,5,4,8,3,7]:当left=1(高度 8)、right=8(高度 7)时,宽度为 7,有效高度为 7,盛水量 = 7×7=49,是最大值; - 示例 2 输入
[1,1]:宽度为 1,有效高度为 1,盛水量 = 1×1=1,符合预期。
总结
- 双指针法的核心是移动较矮的指针,因为盛水量由矮边决定,移动高边无法提升有效高度,只会减少宽度;
- 该解法将时间复杂度从暴力法的 O (n²) 优化到 O (n),是本题的最优解;
- 代码逻辑简洁,关键是理解 "宽度最大优先,逐步优化高度" 的思路。
自己写的js又错了
javascript
/**
* @param {number[]} height
* @return {number}
*/
var maxArea = function(height) {
let left = 0 ;
let right = height.length - 1 ;
let res = 0 ;
while (left < right ){
let wid = right - left ;
let curHeight = height[left];
if (height[left] < height[right]){
curHeight = height[right] ;
}
let cur = wid * curHeight ;
if (cur > res ){
res = cur ;
}
if (height[left] < height[right]){
left ++ ;
}else{
right -- ;
}
}
return res ;
};你这段 JS 代码的核心错误是计算有效高度时搞反了逻辑 ------ 盛水的有效高度应该取两个高度的较小值 ,但你代码里取成了较大值,这直接导致计算出的面积完全错误。
错误定位与分析
先看你代码中计算 curHeight 的关键片段:
javascript
let curHeight = height[left];
if (height[left] < height[right]){
curHeight = height[right] ; // 错误:这里取了较大值,而非较小值
}举个例子:当 height[left]=8、height[right]=7 时,你的代码会把 curHeight 设为 8,但实际容器的有效高度只能是 7(水会从矮的一边溢出),用 8 计算会得出远超实际的面积,结果自然错误。
5 小结
多练习,感觉越做越顺了,双指针这一块还可以了。加油,坚持!