滑动窗口大总结！！！妈妈以后再也不担心我不会做滑动窗口啦~

___Dream2024-08-03 8:04

写在前面：全部题都源于力扣

讲解

滑动窗口算法技巧主要用来解决子数组问题，比如让你寻找符合某个条件的最长/最短子数组。

如果用暴力解的话，你需要嵌套 for 循环这样穷举所有子数组，时间复杂度是O(n^2^)

cpp 复制代码 
for(int i = 0; i < nums.size(); i ++){
	for(int j = i; j < nums.size(); j ++){
		//维护一个nums[i,j]的子数组
	}
}

滑动窗口其实也并不难就是维护一个窗口，不断滑动，不断更新答案，大致逻辑：

cpp 复制代码 
int left = 0, right = 0;

while (right < nums.size()) {
    // 增大窗口
    window.addLast(nums[right]);
    right++;
    
    while (window needs shrink) {
        // 缩小窗口
        window.removeFirst(nums[left]);
        left++;
    }
}

由于这套逻辑left和right都不会回退，所以滑动窗口的时间复杂度是O(n)

没了，讲解到此结束

只学讲解是没有办法乱杀滴，接下来就靠着这个模板魔改解决hard题吧！

题目一：最小覆盖子串

力扣难度hard->传送门

滑动窗口的思路是这样的：

  1. 在字符串 S 中使用双指针中的左右指针技巧，初始化 left = right = 0，把索引左闭右开区间 [left, right) 称为一个「窗口」。

问：为什么设计为左闭右开区间？

答：因为这样初始化 left = right = 0 时区间 [0, 0) 中没有元素，但只要让 right 向右移动（扩大）一位，区间 [0, 1) 就包含一个元素 0 了。如果设置为两端都开的区间，那么让 right 向右移动一位后开区间 (0,1) 仍然没有元素；如果设置为两端都闭的区间，那么初始区间 [0, 0] 就包含了一个元素。这两种情况都会给边界处理带来不必要的麻烦。

  1. 先不断地增加 right 指针扩大窗口 [left, right)，直到窗口中的字符串符合要求（包含了 t 中的所有字符）。
  2. 此时，我们停止增加 right，转而不断增加 left 指针缩小窗口 [left, right)，直到窗口中的字符串不再符合要求（不包含 t 中的所有字符了）。同时，每次增加 left，我们都要更新一轮结果
  3. 重复第 2 和第 3 步，直到 right 到达字符串 s 的尽头。

talk is cheap,show me the code！

首先，需要window和need两个哈希表，用来记录窗口中已有的字符和需要凑齐的字符

cpp 复制代码 
// 记录 window 中的字符出现次数
unordered_map<char, int> window;
// 记录所需的字符出现次数
unordered_map<char, int> need;
for(char c : t) need[c] ++;

现在开始套模板，只需要思考以下几个问题：

  1. 什么时候应该移动 right 扩大窗口？窗口加入字符时，应该更新哪些数据？
    答：只要窗口内没有满足t字符都有的话就应该继续扩大窗口，窗口加入字符时，需要更新窗口大小(window++)，必备字符个数(window[c]++)，已满条件的字符数(valid++)。
cpp 复制代码 
while(right < s.size()){
	char c = s[right];//加入滑动窗口的值
	right ++;//窗口变大
	//新加入的值是否需要,需要的话：
	if(need(c)){
		window[c]++;//已有的必备值加加
		if(window[c] == need[c]) valid++;//如果某个字符在此窗口已经满足条件，valid++
	}
}
  1. 什么时候窗口应该暂停扩大，开始移动 left 缩小窗口？从窗口移出字符时，应该更新哪些数据？
    答：当 valid 满足 need 时应该收缩窗口，应该在收紧窗口的时候更新最终数据，更新窗口大小，更新valid(移除元素了，这里只可能减)，window[字符]数量，另外更新最小覆盖子串的起始位置。因为答案一定是在缩窗口的时候出现的，所以应该在这里更新len和start
cpp 复制代码 
            // 判断左侧窗口是否要收缩
            while (valid == need.size()) {
                // 在这里更新最小覆盖子串
                if (right - left < len) {
                    start = left;
                    len = right - left;
                }
                // d 是将移出窗口的字符
                char d = s[left];
                // 缩小窗口
                left++;
                // 进行窗口内数据的一系列更新
                if (need.count(d)) {
                    if (window[d] == need[d])
                        valid--;
                    window[d]--;
                }
  1. 我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？
    答：一定是在缩小的时候

整体代码：

cpp 复制代码 
class Solution {
public:
    string minWindow(string s, string t) {
        unordered_map<char, int> need, window;
        for (char c : t) {
            need[c]++;
        }
        int left = 0, right = 0;
        // 记录window中的字符满足need条件的字符个数
        int valid = 0;
        // 记录最小覆盖子串的起始索引及长度
        int start = 0, len = INT_MAX;
        while (right < s.size()) {
            // c 是将移入窗口的字符
            char c = s[right];
            // 扩大窗口
            right++;
            // 进行窗口内数据的一系列更新
            if (need.count(c)) {
                window[c]++;
                if (window[c] == need[c])
                    valid++;
            }
           // 判断左侧窗口是否要收缩
           // 用while！！一种缩到不能再缩
            while (valid == need.size()) {
                // 在这里更新最小覆盖子串
                // 必须先将len记录下来再更新窗口大小
                // 只有这样才能记录每一次合法len，然后更新
                if (right - left < len) {
                    start = left;
                    len = right - left;
                }
                // d 是将移出窗口的字符
                char d = s[left];
                // 缩小窗口
                left++;
                // 进行窗口内数据的一系列更新
                if (need.count(d)) {
                    if (window[d] == need[d])
                        valid--;
                    window[d]--;
                }
            }
        }
        // 返回最小覆盖子串
        // 等于INT_MAX的话返回的是""不是" "
        return len == INT_MAX ? "" : s.substr(start, len);
    }
};

题目二：字符串排列

力扣567

mid难度，s1是可以包含重复字符的哦

是明显的滑动窗口算法，相当给你一个 S 和一个 T，请问你 S 中是否存在一个子串，包含 T 中所有字符且不包含其他字符？

基本和题目一是一样的，只有几个地方需要注意：

  1. 本题移动 left 缩小窗口的时机是窗口大小大于 t.length() 时，因为排列嘛，显然长度应该是一样的。
  2. 当发现 valid == need.size() 时，就说明窗口中就是一个合法的排列，所以立即返回 true。至于如何处理窗口的扩大和缩小，和最小覆盖子串完全相同。

完整代码：

cpp 复制代码 
class Solution {
public:
    bool checkInclusion(string t, string s) {
        unordered_map<char, int> need, window;
        for (char c : t) need[c]++;

        int left = 0, right = 0, valid = 0;
        while (right < s.size()) {
            char c = s[right++];
            if (need.count(c)) {
                window[c]++;
                if (window[c] == need[c]) valid++;
            }

            while (right - left > t.size()) { // 严格大于，以便准确控制窗口大小
                char d = s[left++];
                if (need.count(d)) {
                    if (window[d] == need[d]) valid--;
                    window[d]--;
                }
            }
			// valid == need.size()！！！
            if (right - left == t.size() && valid == need.size()) // 确保窗口大小严格等于t的长度
                return true;
        }
        return false;
    }
};

题目三：找所有字母异位词

力扣438

异位词，就是排列啊，搞了个高端的说法，也糊弄不了我们这些绝顶聪明的娃

直接上代码

cpp 复制代码 
class Solution {
public:
    vector<int> findAnagrams(string s, string t) {
        unordered_map<char, int> need, window;
        for (char c : t) {
            need[c]++;
        }

        int left = 0, right = 0;
        int valid = 0;
        // 记录结果
        vector<int> res;
        while (right < s.size()) {
            char c = s[right];
            right++;
            // 进行窗口内数据的一系列更新
            if (need.count(c)) {
                window[c]++;
                if (window[c] == need[c]) {
                    valid++;
                }
            }
            // 判断左侧窗口是否要收缩
            while (right - left > t.size()) {
                char d = s[left];
                left++;
                // 进行窗口内数据的一系列更新
                if (need.count(d)) {
                    if (window[d] == need[d]) {
                        valid--;
                    }
                    window[d]--;
                }
            }
            if(right - left == t.size() && valid == need.size()){
                res.push_back(left);
            }
        }
        return res;
    }
};

题目四：无重复字符的最长子串

力扣3.

这题在双指针里面用双指针解决过了

如果用滑动窗口的话也很容易

窗口缩的条件就是window[c] > 1，说明有重复了

和双指针思路一模一样

双指针：维护[j，i]数组

cpp 复制代码 
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int s[N];
int main(){
    int n;
    int r = 0;
    cin >> n;
    for(int i = 0, j = 0; i < n; i ++){
        cin >> a[i];
        s[a[i]] ++;//记录个数
        while(s[a[i]] > 1){
            -- s[a[j ++]];
        }
        r = max(r, i - j + 1);
    }
    cout << r;
}

滑动窗口：

cpp 复制代码 
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int left = 0;
        int right = 0;
        int r = 0;
        unordered_map<char, int> window;
        while(right < s.size()){
            char c = s[right];
            right++;
            window[c]++;
            while(window[c] > 1){
                char d = s[left];
                window[d]--;
                left++;
            }
            r = max(r, right - left);
        }
        return r;
    }
};

题目五：滑动窗口的最大值

经典滑动窗口，力扣239

又名单调队列的实现

和题目1~4不一样，这题滑动窗口大小固定，每一次的移动也固定，难点在于求最大值

这里实现队列，要有pop，push操作，因为题目的特殊性，再加个返回最大值的max操作

我们需要逐步实现这三个API

push：

push 方法依然在队尾添加元素，但是要把前面比自己小的元素都删掉

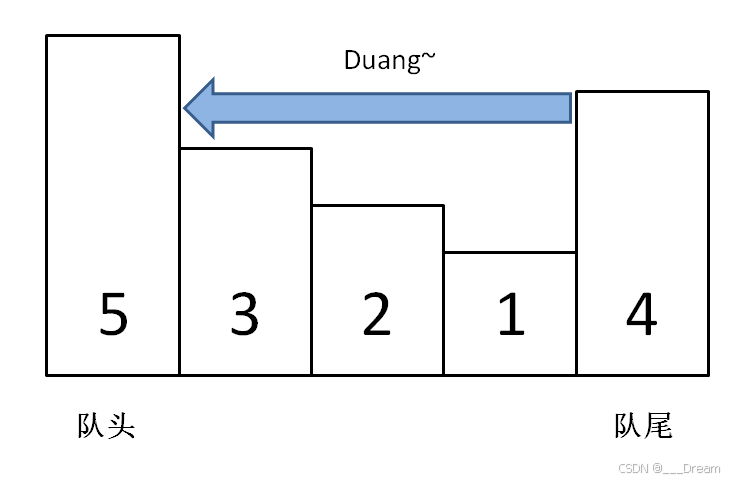
cpp 复制代码 
void push(int n) {
    // 将前面小于自己的元素都删除
    while (!maxq.empty() && maxq.back() < n) {
          maxq.pop_back();
    }
    maxq.push_back(n);
}

max：

如果每个元素被加入时都这样操作，最终单调队列中的元素大小就会保持一个单调递减的顺序，因此我们的 max 方法可以可以这样写：

cpp 复制代码 
int max() {
      // 队头的元素肯定是最大的
      return maxq.front();
    }

pop：

pop 方法在队头删除元素 n：

cpp 复制代码 
void pop(int n) {
     if (n == maxq.front()) {
         maxq.pop_front();
     }
}

所以综合代码：

cpp 复制代码 
class slidingQueue{
private:
    deque<int> maxq;
public:
    void push(int n){
        while(!maxq.empty() && n > maxq.back()) maxq.pop_back();
        maxq.push_back(n);
    }
    int max(){
        return maxq.front();
    }
    void pop(int n){
        if(!maxq.empty() && maxq.front() == n) maxq.pop_front();
    }
};
class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        slidingQueue window;
        vector<int> res;
        for(int i = 0; i < nums.size(); i ++){
            if(i < k - 1){
                window.push(nums[i]);
            }
            else{
                window.push(nums[i]);
                res.push_back(window.max());
                window.pop(nums[i - k + 1]);
            }
        }
        return res;
    }
};
相关推荐
Swift社区39 分钟前
LeetCode - #139 单词拆分
算法·leetcode·职场和发展
Kent_J_Truman1 小时前
greater＜＞() 、less＜＞()及运算符 ＜ 重载在排序和堆中的使用
算法
先鱼鲨生1 小时前
数据结构——栈、队列
数据结构
一念之坤1 小时前
零基础学Python之数据结构 -- 01篇
数据结构·python
IT 青年2 小时前
数据结构 （1）基本概念和术语
数据结构·算法
熬夜学编程的小王2 小时前
【初阶数据结构篇】双向链表的实现（赋源码）
数据结构·c++·链表·双向链表
Dong雨2 小时前
力扣hot100--＞栈/单调栈
算法·leetcode·职场和发展
SoraLuna2 小时前
「Mac玩转仓颉内测版24」基础篇4 - 浮点类型详解
开发语言·算法·macos·cangjie
liujjjiyun3 小时前
小R的随机播放顺序
数据结构·c++·算法
￥ 多多￥3 小时前
c++中mystring运算符重载
开发语言·c++·算法
热门推荐
01(欧拉)openEuler系统添加网卡文件配置流程、(欧拉)openEuler系统手动配置ipv6地址流程、(欧拉)openEuler系统网络管理说明02PyTorch机器学习实现液态神经网络03【HarmonyOS】HUAWEI DevEco Studio 下载地址汇总04玄机平台应急响应—webshell查杀05Coze扣子平台完整体验和实践（附国内和国际版对比）06RAG 实践- Ollama+RagFlow 部署本地知识库07怎样让音频速度变慢？请跟随以下方法进行操作08Unity中PICO实现 隔空取物 和 接触抓取物体09Ubuntu 20.04使用Livox mid 360 测试 FAST_LIO10【目标跟踪】相机运动补偿