【数据结构】六、图：4.图的遍历（深度优先算法DFS、广度优先算法BFS）

三、基本操作

文章目录

三、基本操作
- 1.图的遍历
- - [1.1 深度优先遍历DFS](#1.1 深度优先遍历DFS)
  - - [1.1.1 DFS算法](#1.1.1 DFS算法)
    - [1.1.2 DFS算法的性能分析](#1.1.2 DFS算法的性能分析)
    - [1.1.3 深度优先的生成树和生成森林](#1.1.3 深度优先的生成树和生成森林)
  - [1.2 广度优先遍历BFS](#1.2 广度优先遍历BFS)
  - - [1.2.1 BFS算法](#1.2.1 BFS算法)
    - [1.2.2 BFS算法性能分析](#1.2.2 BFS算法性能分析)
    - [1.2.3 广度优先的生成树和生成森林](#1.2.3 广度优先的生成树和生成森林)
  - [1.3 图的遍历与图的连通性](#1.3 图的遍历与图的连通性)

1.图的遍历

图的遍历是和树的遍历类似，我们希望从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这一过程就叫做图的遍历(Traversing Graph)。

对于图的遍历来，通常有两种遍历次序方案：

深度优先遍历
广度优先遍历

1.1 深度优先遍历DFS

深度优先遍历(Depth First Search)，也有称为深度优先搜索，简称为DFS。

1.1.1 DFS算法

深度优先搜索类似于树的先序遍历。如其名称中所暗含的意思一样，这种搜索算法所遵循的搜索策略是尽可能"深"地搜索一个图，每次都尝试向更深的节点走。它的基本思想如下：

首先访问图中某一起始顶点v，然后由v出发，访问与v邻接且未被访问的任一顶点w1，再访问与 w1 邻接且未被访问的任一顶点...重复上述过程。当不能再继续向下访问时，依次退回到最近被访问的顶点，若它还有邻接顶点未被访问过，则从该点开始继续上述搜索过程，直至图中所有顶点均被访问过为止。

先序遍历：12563478

DFS 最显著的特征在于其 递归调用自身 。同时与 BFS 类似，DFS 会对其访问过的点打上访问标记，在遍历图时跳过已打过标记的点，以确保 每个点仅访问一次。符合以上两条规则的函数，便是广义上的 DFS。算法过程如下：

c 复制代码

bool visited[MAX_VERTEX_NUM];	//访问标记数组

//从顶点出发，深度优先遍历图G
void DFS(Graph G, int v){
	visit(v);	//访问顶点
	visited[v] = TRUE;	//设已访问标记
	//FirstNeighbor(G,v):求图G中顶点v的第一个邻接点，若有则返回顶点号，否则返回-1。
	//NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点，返回除w外顶点v
	for(int w = FirstNeighbor(G, v); w>=0; w=NextNeighor(G, v, w)){
		if(!visited[w]){	//w为v的尚未访问的邻接顶点
			DFS(G, w);//递归
		}
	}
}

但是如果是非连通图，那么就不能从一个结点遍历所有的结点。这个时候需要添加一个函数来寻找没被访问的结点。

c 复制代码

//深度遍历算法final
bool visited[MAX_VERTEX_NUM];	//访问标记数组

//从顶点出发，深度优先遍历图G
void DFS(Graph G, int v){
	visit(v);	//访问顶点
	visited[v] = TRUE;	//设已访问标记
	//FirstNeighbor(G,v):求图G中顶点v的第一个邻接点，若有则返回顶点号，否则返回-1。
	//NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点，返回除w外顶点v
	for (int w = FirstNeighbor(G, v); w>=0; w=NextNeighor(G, v, w)){
		if (!visited[w]){	//w为v的尚未访问的邻接顶点
			DFS(G, w);//递归
		}
	}
}

//对图进行深度优先遍历
void DFSTraverse(MGraph G){
	for (int v=0; v<G.vexnum; v++){
		visited[v] = FALSE;	//初始化已访问标记数据
	}
	for (int v=0; v<G.vexnum; v++){	//从v=0开始遍历
		if(!visited[v]){
			DFS(G, v);
		}
	}
}

1.1.2 DFS算法的性能分析

空间复杂度：DFS算法是一个递归算法，需要借助一个递归工作栈。最坏情况是 O(|V|)。

时间复杂度：

邻接矩阵：需要访问|V|个结点，然后查找|V|个结点的邻接点|V|个，那么时间复杂度为 O(|V|+|V|^2^)。
O(|V|^2^)
邻接表：需要访问|V|个结点，然后查找每个结点的邻接点总共需要O(2|E|)时间，那么时间复杂度为 O(|V|+2|E|)。
O(|V|+|E|)

1.1.3 深度优先的生成树和生成森林

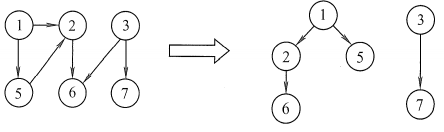
对一个图进行所有结点的遍历，那么在这个遍历过程中不是所有的边都被用到：

**【注意】**1. 从不同的点出发，得到的遍历序列不一样；即使从同一个点出发，也可能得到不同的遍历序列。

因为邻接矩阵的表示方式是唯一的，所以DFS算法得到的遍历序列是唯一的。但是因为单链表的表示方式不是唯一的，所以DFS算法得到的遍历序列不是唯一的。

当图里面有多个连通分量，那么就会有多个生成树，这时候这些树就组成一个生成森林。

1.2 广度优先遍历BFS

广度优先遍历(Breadth First Search)，又称为广度优先搜索，简称BFS。

1.2.1 BFS算法

如果说图的深度优先遍历类似树的前序遍历，那么图的广度优先遍历就类似于树的层序遍历了。

广度优先搜索是一种分层的查找过程 ，每向前走一步可能访问一批顶点，不像深度优先搜索那样有往回退的情况，因此它不是一个递归的算法 。为了实现逐层的访问，算法必须借助一个辅助队列，以记忆正在访问的顶点的下一层顶点。

以下是广度优先遍历的代码：

从结点v出发遍历：

c 复制代码

//邻接矩阵的广度遍历算法。从结点v出发遍历
void BFS(MGraph G, int v){
	Queue Q;
    //把所有结点全部标记为false，表示没有访问过
	for(int i = 0; i<G.numVertexes; i++){
		visited[i] = FALSE;
	}
	InitQueue(&Q);	//初始化一辅助用的队列
    
    visit(v);	//访问顶点
	vivited[v] = TRUE;	//设置当前访问过
    EnQueue(&Q, v);	//将此顶点入队列
            
    //若当前队列不为空
    while(!QueueEmpty(Q)){
        DeQueue(&Q, &v);	//顶点v出队列

        //FirstNeighbor(G,v):求图G中顶点v的第一个邻接点，若有则返回顶点号，否则返回-1。
        //NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点，返回除w外顶点v

        //把出队结点的相邻的所有结点入队
        for(int w=FirstNeighbor(G, v); w>=0; w=NextNeighbor(G, v, w)){
            //检验v的所有邻接点
            if(!visited[w]){
                visit(w);	//访问顶点w
                visited[w] = TRUE;	//访问标记
                EnQueue(&Q, w);	//顶点w入队列
            }//if
        }//for
    }//while
}

但是如果是非连通图，那么就不能从一个结点遍历所有的结点。这个时候需要添加一个函数来寻找没被访问的结点。

c 复制代码

//邻接矩阵的广度遍历算法final
void BFSTraverse(MGraph G){
	int i, j;
	Queue Q;
    //把所有结点全部标记为false，表示没有访问过
	for(i = 0; i<G.numVertexes; i++){
		visited[i] = FALSE;
	}
	InitQueue(&Q);	//初始化一辅助用的队列
    
	for(i=0; i<G.numVertexes; i++){		//这里是从0开始
		//若是未访问过就处理
		if(!visited[i]){
            
        //下面的部分相当于前面写的BFS(G, v);
            
			visit(i);	//访问顶点
            vivited[i] = TRUE;	//设置当前访问过
			EnQueue(&Q, i);	//将此顶点入队列
            
			//若当前队列不为空
			while(!QueueEmpty(Q)){
				DeQueue(&Q, &i);	//顶点i出队列
                
				//FirstNeighbor(G,v):求图G中顶点v的第一个邻接点，若有则返回顶点号，否则返回-1。
				//NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点，返回除w外顶点v
                
                //把出队结点的相邻的所有结点入队
				for(j=FirstNeighbor(G, i); j>=0; j=NextNeighbor(G, i, j)){
					//检验v的所有邻接点
					if(!visited[j]){
						visit(j);	//访问顶点j
						visited[j] = TRUE;	//访问标记
						EnQueue(Q, j);	//顶点j入队列
					}//if
				}//for
			}//while
            
		}//if
	}//for
}

下面的部分相当于前面写的BFS(G, v);，所以还有一种写法是把BFSTraverse 和 BFS分开。

c 复制代码

//对非连通图的广度遍历算法final
void BFSTraverse(MGraph G){
    Queue Q;
    InitQueue(&Q);	//初始化一辅助用的队列
    
	int i;
    //把所有结点全部标记为false，表示没有访问过
	for(i=0; i<G.numVertexes; i++){
		visited[i] = FALSE;
	}
	
    
	for(i=0; i<G.numVertexes; i++){		//这里是从0开始
		//若是未访问过就处理
		if(!visited[i]){
			BFS(G, i);	//调用BFS函数
        }//if
	}//for
}

void BFS(MGraph G, int v){
    visit(v);	//访问顶点
    vivited[v] = TRUE;	//设置当前访问过
    EnQueue(&Q, v);	//将此顶点入队列

    //若当前队列不为空
    while(!QueueEmpty(Q)){
        DeQueue(&Q, &v);	//顶点i出队列

        //FirstNeighbor(G,v):求图G中顶点v的第一个邻接点，若有则返回顶点号，否则返回-1。
        //NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点，返回除w外顶点v

        //把出队结点的相邻的所有结点入队
        for(w=FirstNeighbor(G, v); w>=0; w=NextNeighbor(G, v, w)){
            //检验v的所有邻接点
            if(!visited[w]){
                visit(w);	//访问顶点w
                visited[w] = TRUE;	//访问标记
                EnQueue(Q, w);	//顶点w入队列
            }//if
        }//for
    }//while
}

对于无向图，调用BFS函数的次数 = 连通分量。

1.2.2 BFS算法性能分析

空间复杂度：最坏情况是当所有结点都连在第一个结点上，辅助队列大小为 O(|V|)。

时间复杂度：

邻接矩阵：需要访问|V|个结点，然后查找|V|个结点的邻接点|V|个，那么时间复杂度为 O(|V|+|V|^2^)。
O(|V|^2^)
邻接表：需要访问|V|个结点，然后查找每个结点的邻接点总共需要O(2|E|)时间，那么时间复杂度为 O(|V|+2|E|)。
O(|V|+|E|)

1.2.3 广度优先的生成树和生成森林

对一个图进行所有结点的遍历，那么在这个遍历过程中不是所有的边都被用到：

【注意】因为邻接矩阵的表示方式是唯一的，所以BFS算法得到的遍历序列是唯一的。但是因为单链表的表示方式不是唯一的，所以BFS算法得到的遍历序列不是唯一的。

当图里面有多个连通分量，那么就会有多个生成树，这时候这些树就组成一个生成森林。

1.3 图的遍历与图的连通性

图的遍历算法可以用来判断图的连通性。

对于无向图进行BFS/DFS遍历。

调用BFS/DFS函数的次数 = 连通分量数。
- 若是连通图的，则从任一结点出发，仅需一次遍历就能够访问图中的所有顶点，只需调用1次BFS/DFS。
- 若是非连通的，则从某一个顶点出发，一次遍历只能访问到该顶点所在连通分量的所有顶点，而对于图中其他连通分量的顶点，则无法通过这次遍历访问。
对于有向图 进行BFS/DFS遍历。

调用BFS/DFS函数的次数要具体问题具体分析
- 若起始顶点到其他各顶点都有路径，则只需调用1次BFS/DFS函数，对于强连通图，从任一结点出发都只需调用1次BFS/DFS。
- 但是从起始顶点不能到达所有结点，那么需要调用多次BFS/DFS。