【机器学习】机器学习的基本分类-监督学习-线性回归（Linear Regression）

线性回归是监督学习中的一种基础算法，用于解决回归问题。它通过拟合一条直线（或平面、高维超平面），来预测输出与输入变量之间的关系。

1. 线性回归的基本概念

目标

给定输入和对应的输出 y，找到一个线性函数：

其中：

是权重（回归系数）。
b 是偏置（截距）。
y 是预测值。

损失函数

为了找到最佳的 w 和 b，需要最小化预测值和真实值的误差，常用的误差度量是 均方误差（MSE）：

其中 m 是样本数。

通过优化该损失函数，可以得到最优的参数 w 和 b。

2. 线性回归的假设

线性关系：特征和目标变量之间具有线性关系。
独立性：数据样本是相互独立的。
同方差性：误差的方差相同，不随输入变化。
正态分布：误差服从正态分布。

如果这些假设不能成立，模型的性能可能会下降。

3. 线性回归的实现方式

线性回归可以通过以下两种方式实现：

3.1 正规方程法

通过解析法直接求解参数：

优点：无需选择学习率，计算直接得出结果。
缺点：当特征维度很高时，计算的代价很高。

3.2 梯度下降法

通过迭代优化逐步减小损失函数值：

其中 α\alphaα 是学习率。

优点：适用于大规模数据。
缺点：需要选择合适的学习率，迭代次数较多。

4. Python 实现

4.1 数据生成

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

# 生成模拟数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

plt.scatter(X, y)
plt.xlabel("x")
plt.ylabel("y")
plt.title("Generated Data")
plt.show()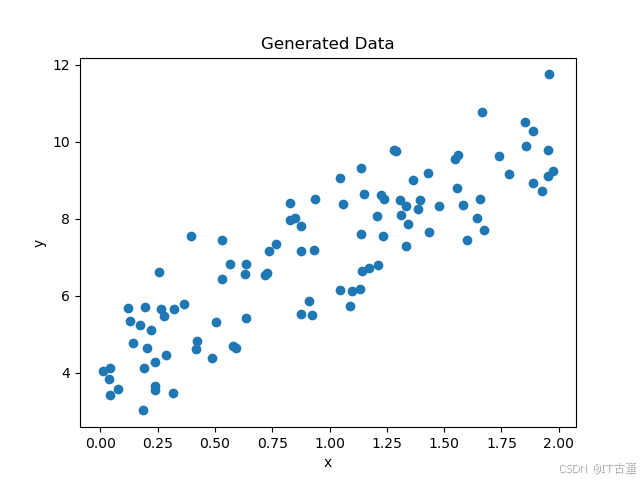

4.2 使用 Scikit-learn 实现

python 复制代码

import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 生成模拟数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 数据集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)

# 模型预测
y_pred = model.predict(X_test)

# 评估模型
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse}")
print(f"Intercept: {model.intercept_}")
print(f"Coefficients: {model.coef_}")

输出结果

bash 复制代码

Mean Squared Error: 0.9177532469714291
Intercept: [4.20634019]
Coefficients: [[2.9902591]]

4.3 自定义实现（梯度下降法）

bash 复制代码

import numpy as np

# 生成模拟数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 初始化参数
m = len(X)
theta = np.random.randn(2, 1)  # [w, b]
X_b = np.c_[np.ones((m, 1)), X]  # 添加偏置列

# 超参数
learning_rate = 0.1
n_iterations = 1000

# 梯度下降
for iteration in range(n_iterations):
    gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
    theta -= learning_rate * gradients

print(f"Optimized Theta: {theta.ravel()}")

输出结果

bash 复制代码

Optimized Theta: [4.22215108 2.96846751]

5. 线性回归的优缺点

优点

简单易用，计算成本低。
结果具有较高的可解释性。
对小数据集表现良好。

缺点

假设特征和目标变量之间具有线性关系，适用性有限。
对异常值敏感。
无法很好地处理复杂的非线性关系。

6. 应用场景

预测分析：如房价预测、销售额预测。
统计建模：解释变量与目标之间的关系。
简单基线模型：为复杂模型提供参考基准。

7. 线性回归的扩展

岭回归（Ridge Regression）：引入 L2 正则化，缓解过拟合问题。
Lasso 回归：引入 L1 正则化，实现特征选择。
多项式回归：扩展到非线性关系，通过增加多项式特征拟合更复杂的模型。