LLM 论文精读（二）Training Compute-Optimal Large Language Models

这篇论文是2022年由DeepMind发表的一篇LLM领域重磅级文章，和上一篇读书笔记 (OpenAI) 发表有关模型规模和性能的论文一样，这篇也是关于模型训练与边界的论文，主要内容是 如何在有限的算力下训练出最优的模型。如果你是从事LLM训练与微调工作的话，这两篇论文都是强烈建议精读的文章。

写在最前面

为了方便你的阅读，以下几点的注意事项请务必了解：

该系列文章每个字都是我理解后自行翻译并写上去的，可能会存在笔误与理解错误，如果发现了希望读者能够在评论区指正，我会在第一时间修正错误。
阅读这个系列需要你有基本的 VLN, LLM, VLM 相关基础知识，有时候我会直接使用英文名词，因为这些词汇实在不容易找到符合语境的翻译。
原文可能因为版面限制存在图像表格与段落不同步的问题，为了更方便阅读，我会在博文中重新对图像表格进行排版，并做到引用图表的文字下方就能看到被引用的图表。因此可能会出现一张图片在博客中多处位置重复出现的情况。
对于原文中的图像，我会在必要时对图像描述进行翻译并附上我自己的理解，但如果图像描述不值得翻译我也不会强行写上去。

Basic Information

论文标题：Training Compute-Optimal Large Language Models
原文链接: https://arxiv.org/abs/2203.15556
发表时间：2022年03月29日
发表平台：arxiv
预印版本号：[v1] Tue, 29 Mar 2022 13:38:03 UTC (10,143 KB)
作者团队：Jordan Hoffmann, Sebastian Borgeaud, Arthur Mensch, Elena Buchatskaya, Trevor Cai, Eliza Rutherford, Diego de Las Casas, Lisa Anne Hendricks, Johannes Welbl, Aidan Clark, Tom Hennigan, Eric Noland, Katie Millican, George van den Driessche, Bogdan Damoc, Aurelia Guy, Simon Osindero, Karen Simonyan, Erich Elsen, Jack W. Rae, Oriol Vinyals, Laurent Sifre
院校机构：
- DeepMind;
项目链接: 【无】
GitHub仓库: 【无】

Abstract

作者研究了在给定计算预算的情况下训练 Transformer 语言模型的最佳模型大小和 token 数量。发现，当前的大型语言模型训练严重不足，这是由于近期人们专注于在保持训练数据量不变的情况下扩展语言模型所致。通过对 50 ～ 5000 亿个 token、参数从 7000 万~160 亿以上的400多个语言模型的研究，作者发现，对于计算优化的训练，模型大小和训练 token 数量应该同等缩放：模型大小每增加一倍，训练 token 数量也应该增加一倍。作者训练了一个预测计算优化的模型 Chinchilla 来验证这一假设，该模型使用与 Gopher 相同的计算预算，但具有 700 亿个参数和 4 倍以上的数据。在大量下游评估任务上，Chinchilla 的表现一致且显著优于 Gopher（280B）、GPT-3（175B）、Jurassic-1（178B）和 Megatron-Turing NLG（530B）。这也意味着 Chinchilla 在微调和推理过程中消耗的计算资源显著减少，从而极大地方便了下游应用。值得一提的是，Chinchilla 在 MMLU 基准测试中达到了 67.5% 的平均准确率，比 Gopher 提升了 7% 以上。

1. Introdution

近年来一系列LLM相继问世，其中最大的密集语言模型目前拥有超过 5000 亿个参数。这些大型自回归 Transformer 已在使用各种评估方案（例如零样本、小样本和微调）的众多任务上展现出令人印象深刻的性能。

训练大型语言模型的计算和能源成本非常高昂，并且会随着模型规模的增加而增加。在实践中，分配的训练预算通常是预先知道的：有多少个加速器可用，以及希望使用它们多长时间。由于这些大型模型通常只能训练一次，因此准确估计给定计算预算下的最佳模型超参数至关重要。

Kaplan 等人的论文表明，自回归语言模型 (LM) 的参数数量与其性能之间存在幂律关系。因此，该领域一直在训练越来越大的模型，期望性能得到提升。Kaplan 等人的一个重要结论是，大型模型不应训练到尽可能低的损失以达到计算最优。虽然本文得出了相同的结论，但作者估计大型模型应该使用比其文章建议的更多token进行训练。具体来说，假设计算预算增加 10 倍，他们建议模型大小应增加 5.5 倍，而训练token数量应仅增加 1.8 倍；相反，作者发现模型大小和训练令牌数量应该按相同比例缩放。

按照 Kaplan 等人和 GPT-3 的训练设置，许多最近训练的大型模型已经训练了大约 3000 亿个 token（Table.1），这与在增加计算量时主要增加模型大小的方法一致。

在本研究中，作者重新审视了这个问题：给定固定的 FLOPs 预算下，如何在模型大小和训练 token 数量之间进行权衡。为了回答这个问题，将最终的预训练损失 L ( N , D ) L(N,D) L(N,D) 建模为模型参数数量 N N N 和训练 token 数量 D D D 的函数关系。由于计算预算 C C C 是已见训练 token 数量和模型参数数量的确定性函数 F L O P s ( N , D ) FLOPs(N,D) FLOPs(N,D)，因此目标是在 F L O P s ( N , D ) = C FLOPs(N,D)=C FLOPs(N,D)=C 的约束下最小化：

N o p t ( C ) , D o p t ( C ) = arg min ⁡ N , D , s . t . F L O P s ( N , D ) = C L ( N , D ) \begin{equation} N_{opt}(C),D_{opt}(C)=\argmin_{N,D,s.t. FLOPs(N,D)=C}L(N,D) \end{equation} Nopt(C),Dopt(C)=N,D,s.t.FLOPs(N,D)=CargminL(N,D)

函数 N o p t ( C ) N_{opt}(C) Nopt(C) 和 D o p t ( C ) D_{opt}(C) Dopt(C) 描述了计算预算 C C C 的最优分配。作者基于 400 多个模型的loss，对函数进行了拟合，这些模型的参数数量从不到 7000 万 ~ 160 亿不等，训练样本量从 50 亿 ~ 4000 亿个 token，每个模型都针对不同的训练范围进行了训练。与 Kaplan 等人的方法相比，得到了截然不同的结果。Fig.1 中重点展示了我们的结果，并在第 2 节中展示了我们的方法有何不同。

根据作者估算的计算最优边界，对于训练 Gopher 所需的计算预算，最优模型应该小 4 倍，同时训练 4 倍以上的 token。在 1.4 万亿 token 上训练一个计算性能更优的 70B 模型 Chinchilla 证明了这一点。Chinchilla 不仅性能优于规模更大的 Gopher，而且其减小的模型尺寸还显著降低了推理成本，并极大地方便了在小型硬件上的下游应用。大型语言模型的能耗成本可以通过其推理和微调来摊销。因此，经过更优化训练的小型模型的优势远不止其性能提升带来的直接好处。

Large language models

近年来，各种大型语言模型应运而生。其中包括密集 Transformer 模型和混合专家 (MoE) 模型。最大的密集 Transformer 模型参数数量已超过 5000 亿。训练越来越大模型的动力显而易见：迄今为止，增加语言模型的规模一直是提升许多语言建模任务的领先地位的关键。然而，大型语言模型面临着诸多挑战，包括其巨大的计算需求（训练和推理的成本会随着模型规模的扩大而增加），以及获取更多高质量训练数据的需求。在本研究中作者发现，更大、更高质量的数据集将在语言模型的进一步扩展中发挥关键作用。

Modelling the scaling behavior

理解语言模型的缩放行为及其迁移特性对于近期大型模型的开发至关重要。Kaplan 等人首次证明了模型大小和损失之间在许多数量级上可预测的关系，研究了在给定计算预算的情况下选择最佳模型大小的问题。与本文类似，他们通过训练各种模型来解决这个问题。作者的工作与 Kaplan 等人在几个重要方面有所不同。首先，他们对所有模型使用固定数量的训练标记和学习率计划；这使得他们无法模拟这些超参数对损失的影响。相反，本文将学习率计划设置为与训练标记的数量大致匹配会产生最佳的最终损失，而与模型大小无关Fig.A1。

对于一个学习率余弦调度到 1300 亿个 token 的固定学习率模型，中间loss估计值（ 0 ≪ 130 B 0 \ll 130B 0≪130B）会高估以 D ′ D^{'} D′ 调度长度训练的模型的损失。使用这些中间损失会低估在少于 1300 亿个 token 的数据上训练模型的有效性，并最终导致这样的结论：随着计算预算的增加，模型大小的增长速度应该比训练数据大小更快。相反，作者认为这两个数量应该以大致相同的速率扩展。其次，这里纳入了参数多达 160 亿的模型，因为观察到 FLOP 损失边界略有弯曲（参见Appendix. E），作者分析中使用的大多数模型都有超过 5 亿个参数，相比之下 Kaplan 等人中的大多数运行都要小得多------许多运行的参数都少于 100M 个。

最近，Clark 等人专门研究了MoE的扩展特性，结果表明，随着模型规模的增加，专家数量对扩展性的贡献会减小，他们的方法将损失建模为两个变量的函数：模型规模 和专家数量。然而，与 Kaplan 等人的方法类似，该分析使用固定数量的训练标记进行，这可能低估了branch带来的提升。

Estimating hyperparameters for large models

在选择语言模型和训练方法时，模型大小和训练标记数量并不是仅有的两个参数。其他重要因素包括学习率、学习率调度、批量大小、优化器和宽深比。本文关注 模型大小 和训练步数，并依靠现有工作和提供的实验启发式方法来确定其他必要的超参数。Yang 等人研究了如何选择用于训练自回归Transformer的各种参数，包括学习率和batch_size。McCandlish 等人发现最佳batch_size和模型大小之间仅有弱依赖性。Shallue 等人与Zhang 等人建议使用比本文更大的batch_size。Levine 等人研究了各种标准模型大小的最佳深宽比。这里使用的深度模型比提议的略少，因为这意味着硬件有更好的wall-clock性能。

Improved model architectures

最近，人们提出了各种有前景的传统密集 Transformer 替代方案。例如，通过使用条件计算，大型 MoE 模型（例如 1.7 万亿参数 Switch Transformer、1.2 万亿参数 GLaM 模型等）尽管使用相对较少的训练和推理 FLOP，却能够提供较大的有效模型大小。然而，对于非常大的模型，路由模型的计算优势似乎会减弱。改进语言模型的一种正交方法是使用显式检索机制来增强 Transformer。这种方法有效地增加了训练过程中可见的数据token数量（在 Borgeaud 等人的论文中增加了 ∼ 10 \sim10 ∼10 倍）。这表明，语言模型的性能可能比之前认为的更依赖于训练数据的大小。

3. Estimating the optimal parameter/training tokens allocation

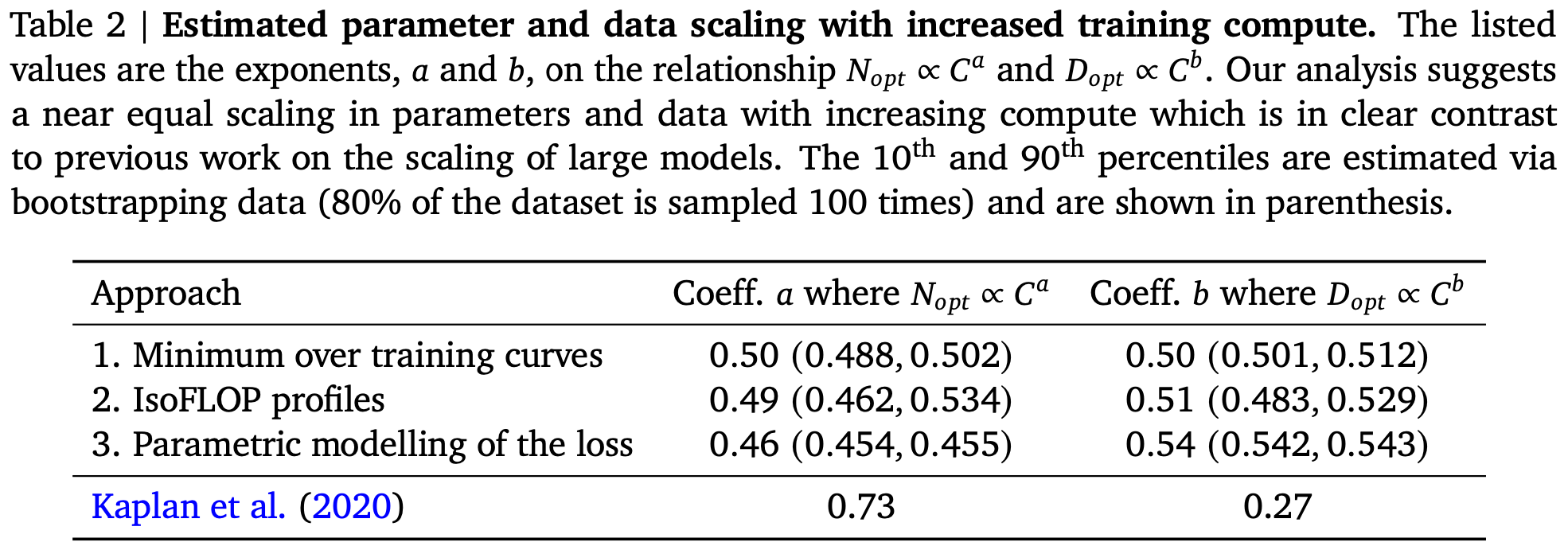
作者提出了三种不同的方法来回答推动我们研究的问题：固定的 FLOP 预算，应该如何在模型大小和训练 token 数量之间进行权衡。在三种情况下都首先训练一系列规模和 token 数量均不同的模型，然后使用得到的训练曲线拟合一个经验估计量，以了解它们的扩展方式。假设计算量和模型大小之间存在幂律关系，就像 Clark 等人和 Kaplan 等人所做的那样，尽管未来的研究可能希望在大型模型的这种关系中包含潜在的曲率。这三种方法得到的预测结果相似，表明参数数量和训练 token 数量应随着计算量的增加而同等增加，比例如Table.2 所示。这与之前关于该主题的研究形成了鲜明对比，值得进一步研究。

3.1. Approach 1: Fix model sizes and vary number of training tokens

在第一种方法中，针对固定的模型系列（参数数量从 7000 万 ~ 100 亿不等）调整训练步数，并为每个模型训练 4 个不同数量的训练序列。通过这些测试可以直接提取给定训练 FLOP 数量下可实现的最小损失的估计值。训练细节可在Appendix. D 中找到，整体步骤如下：

对于每个参数计数 N N N 训练 4 种不同的模型，在以 16 倍范围内（以训练tokens数量衡量），将学习率衰减 10 倍；
对于每次运行平滑并插入训练损失曲线。由此获得每次运行从 FLOP 数到训练损失的连续映射；
对于每个 FLOP 计数，找到哪次运行达到了最低loss，使用这些插值获得从任何 FLOP 计数 c c c 到最有效的模型大小 N N N 和训练token数量 D D D 的映射，使得 F L O P s ( N , D ) = C FLOPs(N,D)=C FLOPs(N,D)=C；
在 1500 个对数间隔的 FLOP 值下，作者发现不同规模的模型实现了最低loss以及所需的训练token数量；
最后拟合幂律，以估算给定计算量的最佳模型大小和训练令牌数量（Fig.2 的中间和右侧），得到 N o p t ∝ C a N_{opt}\propto C^{a} Nopt∝Ca 和 D o p t ∝ C b D_{opt}\propto C^{b} Dopt∝Cb 的关系。

作者发现 a = 0.50 a = 0.50 a=0.50， b = 0.50 b = 0.50 b=0.50 如Table.2 所示。在 D.4 节中展示了 1021 FLOPs 下的比较，分别使用了推荐模型大小和 Kaplan 等人的分析结果，结果表明作者的方法对预测的模型大小非常准确；

3.2 Approach 2: IsoFLOP profiles

在第二种方法中，针对 9 个不同的训练 FLOP 数（范围从 6 × 1 0 18 6\times10^{18} 6×1018 到 3 × 1 0 21 3\times10^{21} 3×1021）设置不同的模型大小，并考虑每个点的最终训练损失。这与Approach 1 在整个训练过程中考虑点 ( N , D , L ) (N,D,L) (N,D,L)不同，能够直接回答以下问题：对于给定的 FLOP 预算，最佳参数数量是多少。

对于每个 FLOP 预算，将平滑后的最终loss与参数数量的关系绘制在Fig.3 (left)。在所有情况都确保训练了足够多样化的模型大小，以便看到损失的明显最小值。对每条 IsoFLOPs 曲线拟合一条抛物线，以直接估算在何种模型大小下实现最小损失Fig3. (left)。与之前的方法一样，在 FLOPs 与损失最优模型大小和训练 token 数量之间拟合幂律，如Fig.3 (center,right)所示。同样拟合形式为 N o p t ∝ C a N_{opt}\propto C^{a} Nopt∝Ca 和 D o p t ∝ C b D_{opt}\propto C^{b} Dopt∝Cb 的指数，发现 a = 0.49 a = 0.49 a=0.49 和 b = 0.51 b = 0.51 b=0.51 如Table.2 所示。

3.3. Approach 3: Fitting a parametric loss function

最后，将Approach 1和Approach 2中实验的所有最终loss建模为模型参数总量与已经输入 token 数量的参数函数。根据经典风险分解（参见 D.2 节）提出以下函数形式：

L ^ ( N , D ) ≜ E + A N α + B D β \begin{equation} \hat{L}(N,D)\triangleq E+\frac{A}{N^{\alpha}}+\frac{B}{D^{\beta}} \end{equation} L^(N,D)≜E+NαA+DβB

公式的第一项描述了理想生成过程在数据分布上的损失，应该与自然文本的熵相对应；第二项描述了一个事实，即一个训练好的参数数量为 N N N Transformer 的性能不如理想的生成过程；最后一项描述了一个事实，即 Transformer 并未经过训练达到收敛，因为只在数据集分布的样本上进行了有限数量的优化步骤。

Model fitting

为了估计 ( A , B , E , α , β ) (A,B,E,\alpha,\beta) (A,B,E,α,β) 使用 L-BFGS 算法最小化预测对数损失和观察到的对数损失之间的 Huber 损失：

min ⁡ A , B , E , α , β ∑ Runs i H u b e r δ ( l o g L ^ ( N i , D i ) − l o g L i ) \begin{equation} \min_{A,B,E,\alpha,\beta}\sum_{\text{Runs} i}Huber_{\delta}\left(log{\hat{L}(N_{i},D_{i})}-log L_{i}\right) \end{equation} A,B,E,α,βminRunsi∑Huberδ(logL^(Ni,Di)−logLi)

通过从初始化网络中选择最佳拟合来考虑可能出现的局部最小值。Huber 损失 ( δ = 1 0 − 3 \delta=10^{-3} δ=10−3) 对异常值具有鲁棒性，作者发现这对于在保留数据点上获得良好的预测性能至关重要。D.2 节详细介绍了拟合过程和损失分解。

Ecient frontier

可以通过最小化参数损失 L ^ \hat{L} L^ 来近似函数 N o p t N_{opt} Nopt 和 D o p t D_{opt} Dopt，前提是 F L O P s ( N , D ) ≈ 6 FLOPs(N,D)\approx6 FLOPs(N,D)≈6。由此得到的 N o p t N_{opt} Nopt 和 D o p t D_{opt} Dopt 平衡了Equation (3) 中依赖于模型大小和数据的两个项。构造如下幂律形式：

N o p t ( C ) = G ( C 6 ) a , D o p t ( C ) = G − 1 ( C 6 ) b , where G = ( α A β B ) 1 α + β , a = β α + β , and b = α α + β \begin{equation} N_{opt}(C)=G\left(\frac{C}{6}\right)^{a},\quad D_{opt}(C)=G^{-1}\left(\frac{C}{6}\right)^{b},\quad\text{where}\quad G=\left(\frac{\alpha A}{\beta B}\right)^{\frac{1}{\alpha+\beta}},\quad a=\frac{\beta}{\alpha+\beta},\text{and}\quad b=\frac{\alpha}{\alpha+\beta} \end{equation} Nopt(C)=G(6C)a,Dopt(C)=G−1(6C)b,whereG=(βBαA)α+β1,a=α+ββ,andb=α+βα

在Fig.4 (left)中展示了拟合函数 L ^ \hat{L} L^ 的轮廓线，并以蓝色表示闭式有效计算前沿。通过这种方法作者发现 a = 0.46 a = 0.46 a=0.46， b = 0.54 b = 0.54 b=0.54 如Table.2 所示。

3.4. Optimal model scaling

作者发现，尽管使用不同的拟合方法和不同的训练模型，三种方法对参数和token的最佳缩放比例以及 FLOPs 的预测结果相当（如Table.2 所示）。这三种方法都表明，随着计算预算的增加，模型规模和训练数据量应该以大致相同的比例增加 。第一种方法和第二种方法对最佳模型大小的预测非常相似，如Fig.1和Fig.A3所示。第三种方法预测，在更大的计算预算下，小模型也将是最佳的。对于低训练 FLOPs ( C ≤ 1 e 21 ) (C\leq1e21) (C≤1e21) 观察到的点 ( L , N , D ) (L,N,D) (L,N,D) 具有比具有更高计算预算的点更大的残差 ∥ L − L ^ ( N , D ) ∥ 2 2 \|L-\hat{L}(N,D)\|^{2}{2} ∥L−L^(N,D)∥22。拟合函数对具有更多 FLOPs 的点增加了权重，由于 Huber 损失，自动将低计算预算点视为异常值。由于经验观察到的边界负曲率 C → N o p t C\to N{opt} C→Nopt（参见Appendix. E），这会导致预测的 N o p t N_{opt} Nopt 低于其他两种方法。

Fig.1	Fig.A3

在Appendix. C 中，作者在另外两个数据集上复现了 IsoFLOP 分析：都得出了类似的结论：模型大小和训练 token 的数量应按相同比例缩放。

4. Chinchilla

根据第 3 节中的分析，Gopher 计算预算的最佳模型规模在 400 亿 ~ 700 亿个参数之间。为了验证这一假设，作者基于该范围的较大值（700 亿个参数）训练了一个模型，该模型使用了 1.4T 的 token，既出于数据集和计算效率的考虑。在本节中，将这个模型Chinchilla与 Gopher 和其他 LLM 进行比较。Chinchilla 和 Gopher 都训练了相同数量的 FLOP，但模型规模和训练 token 数量有所不同。

虽然预训练LLM需要相当大的计算成本，但下游的微调和推理也占用了大量的计算资源。由于比 Gopher 小 4 倍，Chinchilla 的内存占用和推理成本也更低。

4.1 Model and training details

Table.4 给出了用于训练 Chinchilla 的完整超参数集。Chinchilla 使用与 Gopher 相同的模型架构和训练设置，但下面列出的差异除外：

在 MassiveText（与 Gopher 相同的数据集）上训练 Chinchilla，但使用略有不同的子集分布（如表 A1 所示）来解释增加的训练标记数量；
对于 Chinchilla 使用 AdamW 而不是 Adam，因为这可以改善语言建模损失和微调后的下游任务性能；
使用略微修改的 SentencePiece分词器来训练 Chinchilla，该分词器不应用 NFKC 规范化。词汇非常相似，94.15% 的分词与训练 Gopher 时使用的相同。作者发现，这对于数学和化学等概念的表示尤其有帮助。
虽然前向和后向传递均以 bfloat16 类型计算，但在分布式优化器状态中存储了权重的 float32。更多详细信息，请参阅 Rae 等人的实验结果。

在Appendix. G 展示了 Chinchilla 和 Gopher 之间各种优化器相关更改的影响。本分析中的所有模型均在 TPUv3/TPUv4 上使用 JAX 和 Haiku进行训练。在Table. A8 中包含了 Chinchilla 模型信息（这个Table. A8太大了，这里就不额外展示，感兴趣的可以找到原文对应的位置看看）。

4.2 Results

作者对 Chinchilla 进行了广泛的评估，并与各种大型语言模型进行了比较。评估了 Rae 等人论文中提出的大量任务子集，如Table.5所示。由于本研究的重点是实现模型的最佳扩展，因此这里纳入了一个具有代表性的大型子集，并引入了一些新的评估方法，以便更好地与其他现有大型模型进行比较。所有任务的评估细节与 Rae 等人论文中描述的相同。

4.2.1 Language modeling

如Fig.5 所示 Chinchilla 在 The Pile 的所有评估子集上均显著优于 Gopher。与 Lieber et al. 的 Jurassic-1 (178B) 相比，Chinchilla 在除 dm_mathematics 和 ubuntu_irc 两个子集之外的所有子集上均表现出色，原始比特/字节比较结果请参见Table. A5。在 Wikitext103 上，Chinchilla 的困惑度为 7.16，而 Gopher 为 7.75。这些语言建模基准上比较 Chinchilla 和 Gopher 时需要谨慎，因为 Chinchilla 的训练数据比 Gopher 多 4 倍，因此训练集/测试集数据泄漏可能会人为地提高结果。因此，更加重视其他不太受泄漏影响的任务，例如 MMLU 和 BIG-bench 以及各种闭卷问答和常识分析。

4.2.2 MMLU

大规模多任务语言理解 (MMLU) 基准测试包含一系列类似考试的学术科目问题。Table.6 展示了 Chinchilla 在 MMLU 上的平均 5 次测试表现（完整结果见Table. A6）。尽管 Chinchilla 的规模小得多，但它的表现却显著优于 Gopher，平均准确率为 67.6%（比 Gopher 提高了 7.6%）。值得注意的是，Chinchilla 的表现甚至超过了专家对 2023 年 6 月 63.4% 的预测准确率（见Table.6）。此外，Chinchilla 在 4 个不同的独立任务------高中政府与政治、国际法、社会学和美国外交政策上实现了 90% 以上的准确率。据作者所知，目前还没有其他模型在子集上达到 90% 以上的准确率。

Fig.6 展示了 Chinchilla 与 Gopher 按任务细分的比较结果。总体而言，Chinchilla 在绝大多数任务上都提升了性能。但在四项任务（大学数学、计量经济学、道德情景和形式逻辑）中，Chinchilla 的表现不如 Gopher，而在两项任务上 Chinchilla 的表现没有变化。

4.2.3. Reading comprehension

在最终词汇预测数据集 LAMBADA 上，Chinchilla 的准确率达到了 77.4%，而 Gopher 的准确率仅为 74.5%，MT-NLG 530B 的准确率则为 76.6%（见Table.7）。在 RACE-h 和 RACE-m 上，Chinchilla 的表现远超 Gopher，准确率均提升了 10% 以上（见Table.7）。

4.2.4 BIG-bench

利用 Rae 等人论文中的同一组 BIG-bench 任务对 Chinchilla 进行了分析。与在 MMLU 中观察到的情况类似，Chinchilla 在绝大多数任务上的表现均优于 Gopher（见Fig.7），发现 Chinchilla 的平均性能提高了 10.7%，准确率达到 65.1%，而 Gopher 的准确率仅为 54.4%。在 62 个任务中，Chinchilla 仅在四个任务上的表现不如 Gopher：crash_blossom、dark_humor_detection、mathical_induction 和 logical_args。Chinchilla 的完整准确率结果可在Table.A7 中找到。

4.2.5 Common sense

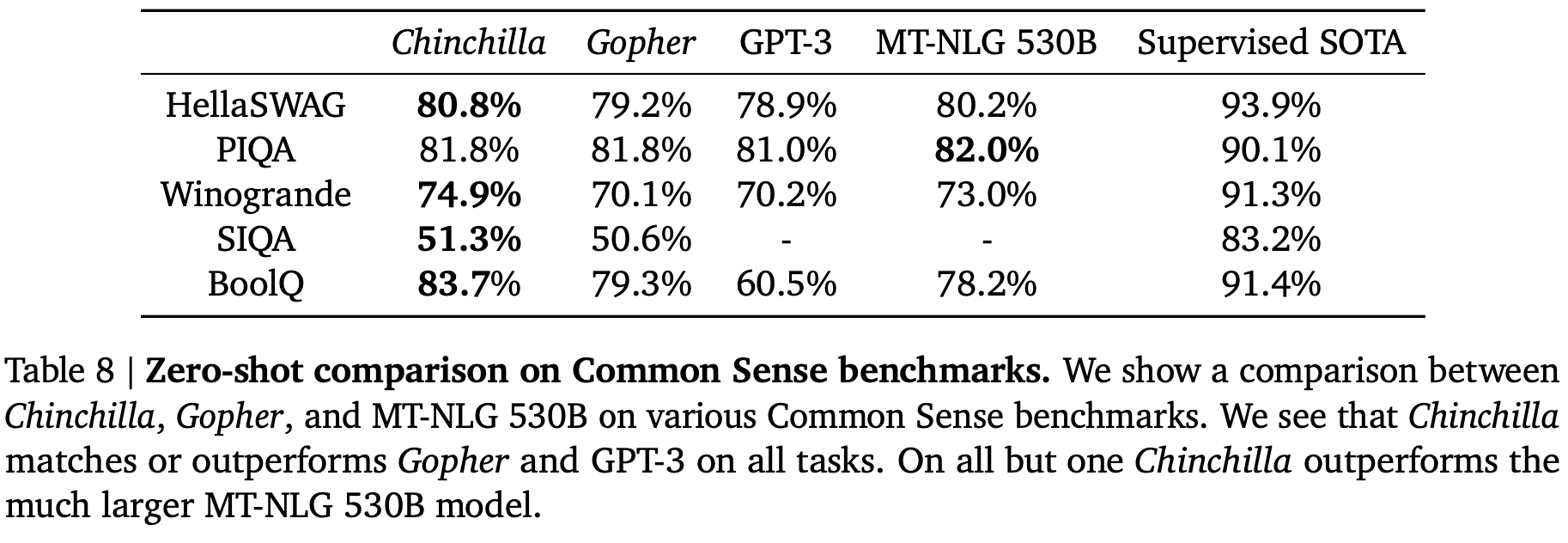
作者基于各种常识性基准对 Chinchilla 进行了评估：PIQA、SIQA、Winogrande、HellaSwag和 BoolQ，发现Chinchilla 在所有任务上的表现均优于 Gopher 和 GPT-3，并且在除一项任务外的所有任务上均优于 MT-NLG 530B（见Table.8）。

在 TruthfulQA上，Chinchilla 在 0 次、5 次和 10 次测试中分别达到了 43.6%、58.5% 和 66.7% 的准确率。相比之下Gopher 的 0 次和 10 次准确率分别仅为 29.5% 和 43.7%。与 Lin et al. 的研究结果形成鲜明对比的是，Chinchilla 取得的显著提升（0 次准确率提高了 14.1%）表明，仅凭对预训练数据进行更佳的建模就能在该基准上取得显著提升。

4.2.6. Closed-book question answering

Table.9 报告了闭卷问答基准测试的结果。在 Natural Questions 数据集上，Chinchilla 取得了新的闭卷 SOTA 准确率：5 次样本准确率为 31.5%，64 次样本准确率为 35.5%，而 Gopher 的准确率分别为 21% 和 28%；在 TriviaQA上展示了过滤集（之前用于检索和开卷工作）和未过滤集（之前用于大型语言模型评估）的结果。在这两种情况下，Chinchilla 的表现都远远优于 Gopher。在过滤集上，Chinchilla 仅落后于开卷 SOTA 7.9%。在未过滤集上，Chinchilla 的表现优于 GPT-3，参见Table.9。

4.2.7. Gender bias and toxicity

大型语言模型存在潜在风险，例如输出攻击性语言、传播社会偏见以及泄露隐私信息。作者预计 Chinchilla 的风险与 Gopher 类似，因为 Chinchilla 使用相同的数据进行训练（尽管相对权重略有不同），并且架构相似。本文将探讨性别偏见（尤其是性别和职业偏见）以及恶意语言的生成。选取一些常见的评估来突出潜在问题，但需要强调的是，这里的评估并不全面，在理解、评估和降低 LLM 风险方面仍有许多工作要做。

Gender bias

正如 Rae 等人所讨论的，大型语言模型能够从其训练数据集中反映出关于不同群体（例如性别群体）的当代和历史话语，作者预计 Chinchilla 也应如此。本文使用 Winogender 数据集在零样本环境下，测试潜在的性别和职业偏见是否会在共指消解的不公平结果中体现出来。Winogender 测试模型能否正确判断代词是否指代不同的职业词汇。无论代词的性别如何，无偏见的模型都能正确预测代词所指代的词汇。遵循与 Rae 等人相同的设置（详见 H.3 节）。

如Table.10所示，Chinchilla 正确解析代词的频率都高于 Gopher。男性代词（增幅 3.2%）的性能提升远小于女性代词或中性代词（增幅分别为 8.3% 和 9.2%），这里还考虑了"陷阱"示例，其中正确的代词解析与性别刻板印象相矛盾（由劳工统计数据确定）。Chinchilla 解析代词的准确性高于 Gopher。当按男性/女性和"陷阱"/"非陷阱"分类示例时，最大的改进出现在女性"陷阱"示例上（改进了 10%）。尽管 Chinchilla 在更多共指示例上一致克服了性别刻板印象，但某些代词的改进率高于其他代词，这表明使用计算更优化的模型所带来的改进可能并不均衡。

Sample toxicity

语言模型能够生成恶意语言，包括侮辱、仇恨言论、亵渎和威胁。虽然"恶意"是一个总称，且在语言模型 (LM) 中评估其难度较大，但自动分类器得分可以指示语言模型生成的有害文本的级别。Rae 等人发现，通过增加模型参数数量来改善语言模型损失对恶意文本生成（未经提示）的影响微乎其微；本文分析了通过更优化计算的训练实现的更低语言模型损失是否也适用同样的效果。与 Rae 等人的方案类似，从 Chinchilla 中生成了 25,000 个无提示样本，并将它们的 PerspectiveAPI 毒性得分分布与 Gopher 生成的样本进行比较。一些汇总统计数据表明没有重大差异：Gopher 的平均（中位数）毒性得分为 0.081（0.064），而 Chinchilla 为 0.087（0.066），Gopher 的第 95 个百分位得分为 0.230，而 Chinchilla 为 0.238。也就是说，绝大多数生成的样本被归类为无毒，模型之间的差异可以忽略不计。与先前的研究结果一致，这表明无条件文本生成中的毒性水平在很大程度上与模型质量（以语言建模损失来衡量）无关，即训练数据集的更好模型不一定更具毒性。

5. Discussion & Conclusion

到目前为止，大型语言模型训练的趋势是增加模型规模，而通常不会增加训练标记的数量。最大的Transformer MT-NLG 530B 现在比两年前 GPT-3 的 1700 亿个参数大了 3 倍多。然而，该模型以及大多数现有的大型模型都是使用数量相当的token（约 3000 亿个）进行训练的。虽然训练这些巨型模型的愿望已经带来了大量的工程创新，但作者推测，训练越来越大的模型的竞争会导致模型的性能远低于在相同计算预算下可以实现的性能。

基于超过 400 次训练的结果，作者提出了三种预测方法来优化模型大小和训练时长。这三种方法都预测 Gopher 的规模过大，并估计在相同的计算预算下，使用更多数据训练的较小模型将表现更好。通过训练一个 70B 参数的模型 Chinchilla 来直接验证这一假设，结果表明它在几乎所有测量评估任务上都优于 Gopher 甚至更大的模型。

虽然作者的方法能够预测在额外计算资源的情况下如何扩展大型模型，但也存在一些局限性。由于训练大型模型的成本较高，只有两次可比的大规模训练运行（Chinchilla 和 Gopher），并且没有中等规模的额外测试。此外，作者假设有效的计算前沿可以通过计算预算、模型大小和训练token数量之间的幂律关系来描述。然而，作者观察到在高计算预算下， l o g ( N o p t ) log(N_{opt}) log(Nopt) 存在一些凹度（参见Appendix. E）。这表明可能仍然高估了大型模型的最佳规模。最后分析训练运行均基于少于一个 epoch 的数据进行训练；未来的工作可能会考虑多个 epoch 方案。尽管存在这些局限性，Chinchilla 与 Gopher 的比较验证了我们的性能预测，从而能够在相同的计算预算下训练出更好（且更轻量级）的模型。

尽管近期已有多项研究致力于训练越来越大的模型，但作者实验表明，需要更加重视数据集的扩展。作者推测，只有在数据质量高的情况下，扩展到越来越大的数据集才有益。这要求采集更大的数据集，并高度重视数据集质量。更大的数据集需要格外小心，以确保训练集和测试集的重叠得到妥善考虑，这不仅体现在语言建模损失函数中，也体现在下游任务中。最后，对数万亿个词条进行训练会引发许多伦理和隐私问题。从网络上抓取的大型数据集可能包含恶意言论、偏见和隐私信息。随着数据集规模的扩大，此类信息的数量（如果不是频率的话）也会增加，这使得数据集自省变得更加重要。Chinchilla 确实受到偏见和恶意的影响，但有趣的是，它受到的影响似乎比 Gopher 要小。更好地理解大型语言模型的性能与恶意如何相互作用是未来的一个重要研究课题。

虽然作者已将该方法应用于自回归语言模型的训练，但预计在其他模态中，模型大小和数据量之间也存在类似的权衡。由于训练大型模型的成本非常高，因此事先选择最佳模型大小和训练步骤至关重要。作者提出的方法在新的环境中易于复现。